0 引言
光电经纬仪具有性能稳定、精度高、抗干扰能力强的优势[1-2]。靶场试验任务常采用多台光电经纬仪对同一飞行器目标进行交会测量,主要过程有:目标捕获、编码器数据生成、数据传输,数据接收与交会计算等[3],最终得到精确轨迹等弹道参数,这要求测控系统的每台光电经纬仪尽可能保证测量数据的及时和准确。光电经纬仪属于测角体制仪器,长焦镜头视场角小,仅靠手动单杆控制经纬仪在大范围视场内进行搜索,独立捕获目标的难度较大[4-5],在外引导跟踪模式下,中心站实时把目标的位置信息发送给光电经纬仪,从而使得目标进入视场。且当图像闭环跟踪模式中图像判读失效时[6],外引导模式可保证光电经纬仪跟踪过程的继续进行,待图像判读及脱靶量提取稳定,可以选择切换回图像闭环跟踪模式,因此外引导模式是经纬仪工作模式的重要组成部分[7]。
目标相对于经纬仪方位角和俯仰角的实时测量,是事后处理及整个测量任务的基础,外引导模式下,不准确和不平滑的引导信息,图像获取不稳定,导弹等空间目标轨迹计算的精确性下降[8-9],因此有必要提出外引导数据的实时平滑算法以保证其准确性和平滑性。外引导可由多种测量体制获得,如遥测、雷达等[10]。受环境干扰、设备精度等因素的影响,外引导数据往往含有野值[11],并且其频率往往低于光电经纬仪控制信号的频率,因此平滑算法需要判别和替代其中的野值[12-13],并插值得到合适帧率的数据作为光电经纬仪真正的引导数据。
在野值剔除方面,国内学者已有大量研究。野值点可根据是否连续出现分为孤立型和连续型。文献[14]对目前工程中常见的几种野值处理方法进行实验分析,多项式外推拟合法流程简单,剔除孤立型野值效果明显,但对于连续型野值效果一般,判别门限不易确定。文献[15]提出利用小波去噪算法剔除野值,剔除效果较好,但无法应用于实时处理场景中。文献[16]提出了利用灰色预测进行自适应野值判别的方法,但对于连续型野值来说,同样难以起到理想效果。
在插值处理方面,靶场光电经纬仪常用的插值算法是线性最小二乘插值法和牛顿插值法等方法。然而在实际任务中,外引导数据出现“卡顿”现象,即连续多帧为相同值,此时一般的插值算法无法保证平滑,容易造成光电经纬仪跟踪过程中运动剧烈、机架抖动,存在损坏伺服系统的风险。目前靶场测控多数采用线性插值[17],关于外引导卡顿数据的平滑处理,研究极少。
针对以上问题,提出了外引导平滑算法,包含基于动态门限的外引导野值处理算法与基于自适应插值的处理算法。
1) 野值处理算法,解决了样本点含有异常值时,样本方差估计不准确的问题,构建动态门限判别野值,检测率和虚警率均优于固定门限等方法。
2) 插值处理算法能应对外引导数据卡顿带来的不连贯性,根据外引导数据自适应计算插值点。
上述外引导平滑算法已成功应用于海军某靶场测控站。
1 基于动态门限的野值处理
常见的外弹道测量的野值处理方法有以下几种:一是在分析数据统计特性基础上,通过计算标准差等设置合理的阈值对野值进行判别和剔除,有莱特准则、罗曼诺夫斯基准则[18]等;二是通过提取并分析数据特征对野值进行判别和剔除,有小波变换方法[15-19]等;三是求取并分析数据的滤波估计值与原始值差的统计特性来进行判别[20-22]。
工程中常用的实时野值处理算法是利用当前时刻之前的数据点计算外推值,并构造门限,当外推值与当前实际接收值差值超出该门限外,则认为此时的接收值为野值,以外推值替代,因此数据外推与门限构造对于野值处理起着关键作用。针对野值判别门限不易确定、不够准确的问题,通过影响函数计算样本方差,从而构造得到动态门限。
1.1 常见的野值处理算法
选取当前时刻之前的五点数据,五点外推公式如式(1)所示。当前时刻记为yk,五点时刻分别为yk-5,yk-4,…,yk-1
(1)
由莱特准则可知,当数据服从正态分布时,数据点与样本均值间的残差大部分落在3倍标准差之内,超过此范围的概率不超过0.3%[23],假设时刻k中心机发送的外引导数据yk与五点外推数据
之间的残差Δyk服从均值为0的正态分布[24],并记Δyk的样本标准差为
野值处理准则如下:
为正常值,不处理
为野值,yk替换为
每一时刻计算五点外推值
及残差值Δyi,取当前时刻之前的n点作为滑动窗口,记窗口内测量数据序列为{yi},外推数据序列为
则残差序列为{Δyi},其中
利用式(2),进而可以得到3倍样本标准差。
(2)
1.2 基于动态门限的野值处理算法
在实际的跟踪测量过程中,滑动窗口内数据点可能存在异常值,尤其是连续型野值点,前后几个连续采样点也是野值,按照式(2)计算的样本方差无法体现滑动窗口内数据的差异,将不再是准确的估计值,判别门限也同样不再准确,因此需要对样本方差的求解进行改进。
假设已知数据存在一个先验标准差σ,同时规定阈值CH,区分滑动窗口内数据为正常值或异常值的规则如下:
|Δyi/σ|<CH, yi为正常值
|Δyi/σ|≥CH, yi为异常值
值得注意的是,算法利用先验标准差σ用于区分滑动窗口内数据为正常值或异常值,而非直接作为野值判别所用的样本标准差。
利用影响函数得到的样本方差计算公式,如式(3)所示。
(3)
式(3)中:ψ(x)为影响函数;
为待求解的样本标准差;β为待定参数,影响函数的作用就在于区分滑动窗口内的正常值点和异常值点,并利用正常值点得到更准确的样本方差。
选择Huber的ψH(x)函数作为影响函数[25],为分段函数的形式
(4)
式(3)中:是未知的,计算时
无法直接确定,只有滑动窗口内的正常点才会体现准确的样本方差,因此借助正常值或异常值的区分标准,处理如下
(5)
记Mn为滑动窗口内正常值点构成的集合,NH为滑动窗口内异常值点的数目,将式(5)代入式(3),得到自适应样本方差,如式(6)所示。
(6)
(7)
先验阈值CH,先验标准差σ均为设定值,因此方差估计的关键是β参数的求取,可写为如下形式
(8)
一般而言,异常值点不会改变滑动窗口内Δyi的分布特性,假设残差服从均值为0的正态分布,正态分布的标准差取为设定的先验标准差,即Δyi～N(0,σ2),Δyi/σ～N(0,1)。
已知正常值点是滑动窗口内满足|Δyi/σ|<CH的点,同时对应的Δyi/σ服从标准正态分布,因此正常值点服从截断正态分布[26],即Δyi/σ～N(0,1;-CH,CH),此截断正态分布的数学期望和方差分别记为
集合Mn内数据点个数记为Nn。并且式(2)中,样本方差替换为方差仍可认为成立。综上,正常值点满足如下关系
(9)
将式(9)代入式(8),可写为如下形式
(10)
无论是正常值或异常值点都满足Δyi/σ～N(0,1),数据点数量的比例可以认为近似等于分布概率,记P1为随机变量Δyi/σ分布在区间[-CH,CH]的概率,P2为分布在区间[-∞,-CH]∪[CH,+∞]的概率,则(Nn-1)/(n-1)和NH/(n-1)可以分别利用P1和P2表示,标准正态分布的概率分布函数记为Φ(x),具体计算方式如下
(11)
联立式(10)、式(11),求出对应于不同CH的β。
表1 CH及其对应β值
Table 1 CH and its corresponding β
CH1.21.31.41.51.61.7β0.514 90.567 70.617 90.665 00.708 70.748 9
特别地,当CH→+∞,P1→1,此时β→1,影响函数ψ(x)=x,式(6)将退化为式(2),式(6)可认为是样本方差的统一形式,式(2)视为式(6)的特例。
野值处理算法流程如下:
1) 当前时刻接收外引导数据,计算五点外推值,残差Δyk。
2) 由当前时刻前n点所构成的滑动窗口内的残差序列{Δyi},统计异常值点数目NH。
3) 由式(6)计算样本标准差
取
作为动态门限。
4) 依据野值判别准则,比较|Δyk|与
进行处理。
实际试验任务中,当残差绝对值过小,不进行野值判别,当连续的外引导数据,例如40点,都判断为野值点,且为相同值,可判定为经纬仪的定点引导数据,此时清空数据变量,重新开始检择判别。
2 自适应插值处理算法
某型靶场经纬仪伺服系统的控制信号为100 Hz,而中心站的外引导数据只有20 Hz。插值算法每接收一个外引导数据点,应当插值得到五点数据。作为经纬仪伺服系统直接使用的数据,插值之后的外引导数据应当平滑连贯,当前经纬仪方位或俯仰沿某一方向转动时,插值数据的增减性不能出现剧烈变化,否则会严重损害经纬仪的伺服系统。针对以上问题,提出自适应插值处理算法。
2.1 常见的插值处理算法
2.1.1 线性最小二乘法
假设当前时刻为k,当前时刻接收的20 Hz外引导数据为yk,选取当前时刻及之前的外引导数据,例如选取10点yk-9yk,…,yk,构造最小二乘意义下的线性方程,得到 k-0.8, k-0.6,…,k时刻的五点插值数据,作为100 Hz的实际引导数据。
2.1.2 牛顿插值法
当外引导为固定频率数据的等距结点,此时可进一步简化牛顿插值法,这里以前向插值公式[27]为例。
(12)
其中,Δfi=fi+1-fi,Δkfi=Δk-1fi+1-Δk-1fi
对于靶场外引导数据,二次曲线即可表征曲线形态,因此n取为2,x0取为当前yk,h取为-1,将t=0.8,0.6,…,0代入式(12),得到k-0.8,k-0.6,…,k时刻的插值数据。
2.2 外引导的卡顿现象
外场中心联调时,会遇到中心站发送的外引导数据连续多帧为相同数据,称为“卡顿”数据,如图1(a)所示为经纬仪接收的方位角外引导数据。形成此现象的原因往往是外引导的探测源采样率较低,还可能是中心站切换数据源[28],导致发送的外引导数据无法及时更新,保持在与之前时刻相同的值。
图1 卡顿点及其插值数据
Fig.1 Stuck point and interpolation data
卡顿情况下,采用线性最小二乘法或牛顿插值法的插值数据分别如图1(b)、图1(c)所示。图中经纬仪当前方位角度为递增趋势,插值数据应当保持此趋势,而2种方法产生的插值数据明显前后不连贯、剧烈波动。图中得到的插值数据,存在小于前一点的插值数据点,不符合当前的递增趋势,若直接作为伺服系统的控制信号,使得经纬仪跟踪过程中在相反的转动方向上急速切换、频繁启停,在实际试验中,这会引起经纬仪机架抖动,甚至会损害伺服系统。
对于线性最小二乘法,虽然利用线性方程能够较好保留参与插值的样本点整体的趋势,但是当卡顿点出现时,不同插值时刻得到的五点数据之间不连贯。对于牛顿插值法,虽然能够构造二次曲线或更高次曲线,但是牛顿插值法严格利用每一个新接收的外引导点构造差商,插值多项式会严格经过插值节点,这就产生了曲线上具有不同凹凸性的弧段,增减性的变化同样会使得经纬仪抖动剧烈。因此针对2种方法的不足,本文提出基于自适应插值的处理算法。
2.3 基于自适应插值的处理算法
算法的目的是利用20 Hz的接收数据插值得到100 Hz的插值数据。当前时刻接收的引导数据记为yk,最近接收的十点数据记为yk-9,yk,…,yk,前一接收时刻得到的五点插值为zk-1.8,zk-1.6,…,zk-1,当前所求的插值数据记为zk-0.8,zk-0.6,…,zk。定义有效点为与前一时刻值相异的引导数据点,而卡顿点与前一时刻引导值相同,并且根据卡顿点连续出现的数目L将卡顿点分为2类:轻微卡顿点与严重卡顿点,L可取为经验值。轻微卡顿点是指当前卡顿点是已连续出现的数目小于等于L的卡顿点,而严重卡顿点已连续出现的数目大于L。若yk为有效点,则更新标志位flag,标记此时方位角或俯仰角递增或递减的走向,当此有效点的角度值大于接收的前一外引导值,即引导角度值递增时,flag记为1;反之,flag记为-1。卡顿点时,flag保持上一时刻原值。
自适应插值使用线性最小二乘法由十点外引导值计算得到LS[0],…,LS[4],在此基础上引入2次连贯性判断。
第1次是判断线性最小二乘法得到的当前五点插值数据与上一次插值的五点数据趋势是否连贯。例如flag>1,当前外引导呈递增趋势,上一次得到插值数据不应大于此次的插值结果,具体来说是判断flag×(LS[0]-zk-1)的正负,若为负值,说明LS[0]相对于zk-1不连贯。则LS[0],…,LS[4]不能直接作为最后插值数据,应当保证此次插值的角度继续增加。
第2次是判断新接收的外引导数据yk相对于上一次插值的五点数据是否连贯,例如flag>1,上一次得到插值数据不应大于当前接收的外引导数据,具体是判断flag×(yk-zk-1)的正负,若为负值,说明上一次插值时刻所引导的角度位置已经超过了当前有效点所指示的位置,yk相对于zk-1不连贯。同时为了保证经纬仪不会反方向回转,所以只能允许当前插值的五点只增加微小的增量,由increment来约束。
本文提出的自适应插值处理算法将线性最小二乘法的输出作为中间结果进行连贯性判断,根据外引导数据点的分类,算法具体由以下流程构成:
若yk为有效点,算法流程如下:
1) 更新flag。
2) 根据线性最小二乘法,由yk-9,yk,…,yk计算得出LS[0],…,LS[4]。
3) 判断flag×(LS[0]-zk-1)<0,若成立,继续执行步骤(4);否则,LS[0],…,LS[4]即可作为zk-0.8,zk-0.6,…,zk,结束流程。
4) 判断flag×(yk-zk-1)<0的正负,若成立,zk-i=zk-1+flag×increment×(1-i),否则,按照yk与LS[0]2点间距选取插值数据,即zk-i=zk-1+flag×|LS[0]-yk|×(1-i),其中i=0.8,0.6,…,0。
对于轻微卡顿点,通过第1次判断来保证不同接收时刻的插值数据各段连贯。由于外引导此时卡顿,zk-1会逐渐超过yk,因此不进行第2次判断,而是保证卡顿点的插值数据相对于yk不会出现大幅度的偏离,不要超过设定阈值threshold,否则可能导致经纬仪捕获不到实际目标。
若yk为轻微卡顿点,算法流程如下:
1) 根据线性最小二乘法,由yk-9,yk,…,yk计算得出LS[0],…,LS[4]。
2) 判断flag×(LS[0]-zk-1)<0,若成立,继续执行步骤(3);否则,LS[0],…,LS[4]即可作为zk-0.8,zk-0.6,…,zk,结束流程。
3) 判断|yk-zk-1|>threshold,若成立,zk-i=zk-1+flag×|LS[0]-yk|×(1-i);否则zk-i=zk-1+flag×increment×(1-i),其中i=0.8,0.6,…,0。
对于严重卡顿点,因为有效点能反映方位俯仰的基本走向,因此选取最近邻的3个有效点作为外引导数据的特征点,外加3个卡顿点,此6点共同构造线性最小二乘五点插值数据,使得插值数据反映曲线趋势。严重卡顿时的插值点,不应偏离接收的外引导(此时仍为卡顿点)过大,故同样判断是否超过阈值threshold。其余步骤与前面所述相同,不再阐述。
若yk为严重卡顿点,算法流程如下:
1) 选取离当前接收外引导点最近的3个有效点,外加最近的3个卡顿点yk-2,yk-1,yk来构造线性最小二乘五点插值数据,计算结果仍然记为LS[0],…,LS[4]。
2) 计算LS[0],…,LS[4]所在直线的斜率,记为slope。
3) 判断flag×(LS[0]-zk-1)<0,若成立,继续执行步骤(4);否则,LS[0],…,LS[4]即可作为zk-0.8,zk-0.6,…,zk,结束流程。
4) 判断|yk-zk-1|>threshold,若成立,沿斜率为slope的直线选取插值数据,即zk-i=zk-1+slope×(1-i);否则zk-i=zk-1+flag×increment×(1-i),其中i=0.8,0.6,…,0。
自适应插值处理算法的数学原理与线性最小二乘法相同,但后者不考虑2次插值之间、插值数据与接收数据之间的关联,自适应插值处理算法使得相邻2次插值数据严格保持着一致的连贯性,与接收的外引导数据整体趋势一致。
3 实验结果与分析
3.1 野值处理算法
3.1.1 实验设置
野值处理算法的实验包含仿真实验与实际外场试验,所用数据是经坐标转换后的角度引导数据。
仿真实验选取一段未出现野值的实际外场试验数据,添加若干野值,分别使用动态门限、固定门限、无影响函数的野值处理方法,固定门限方法取自适应门限计算中先验标准差σ的3倍,无影响函数方法的判别门限取式(2)样本标准差的3倍,本文方法取CH=1.7,滑动窗口长度n=50,3种方法除判别门限不同外,其余条件完全相同。
实际外场试验中,算法编译、集成于主控软件,记录接收和实时处理后的外引导数据,分析算法实际效果。主控软件属于经纬仪的机下操控软件[29],其通过高速局域网或串口与机上多路复合跟踪器进行数据通讯,通过以太网与远端中心机进行数据通讯。主控软件作为系统的直接操控软件,实现对整个设备的监视、设置、检测及调试等功能。
3.1.2 仿真实验
实验添加50处的孤立型野值点,5处长度为随机5～10的连续性野值点,添加野值后的引导数据与3种方法分别处理的结果如图2所示,计算3种野值处理方法的系统误差[30],结果如表2所示。
图2 3种方法的野值处理结果
Fig.2 The outlier processing results of three methods
表2 系统误差对比
Table 2 Comparison of the system error
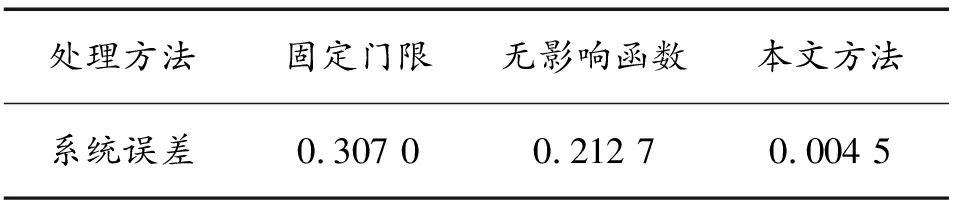
处理方法固定门限无影响函数本文方法系统误差0.307 00.212 70.004 5
连续仿真20次,野值设置条件不变。定义判别检测率=剔除数目中的野值数目/添加的野值点总数;虚警率=(总剔除数目-剔除数目中的野值数目)/总剔除数目,3种方法的检测率、虚警率与系统误差对比如图3所示。
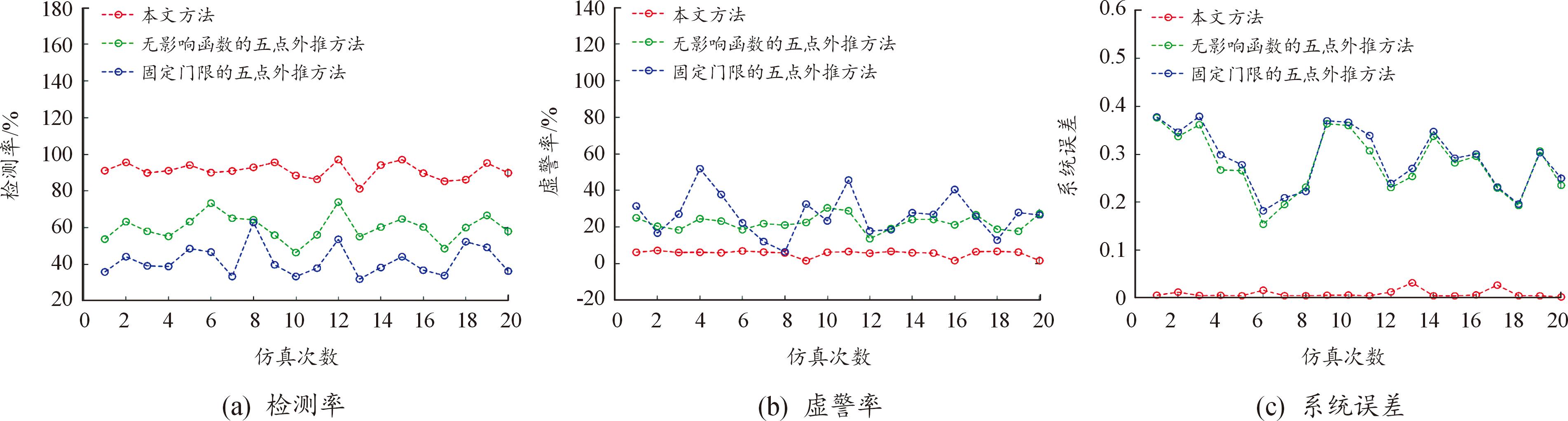
图3 仿真实验的处理结果
Fig.3 Processing results of simulations
3.1.3 外场实验
针对某次外场试验的记录数据进行处理,如图4所示。
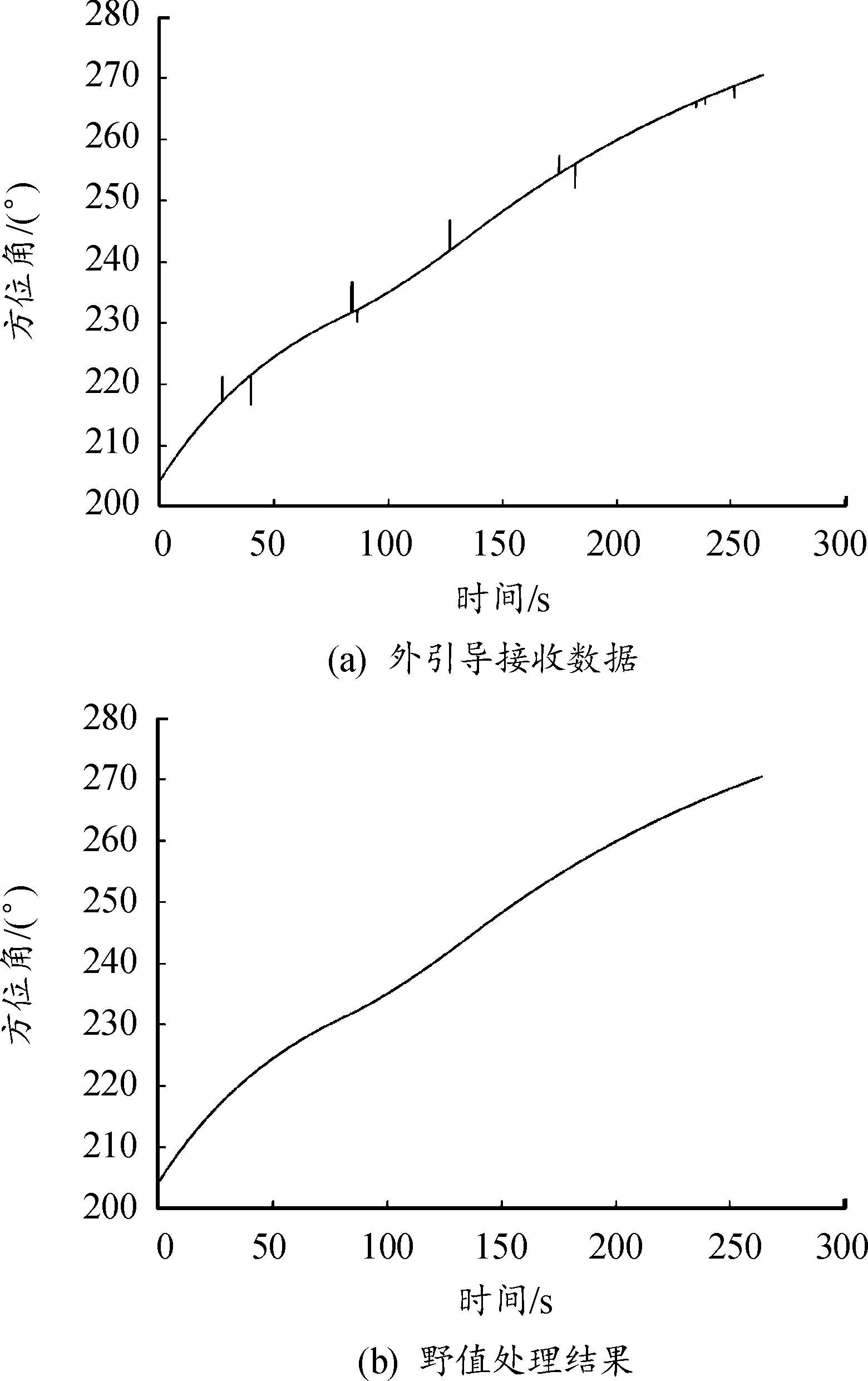
图4 外场试验的野值处理结果
Fig.4 Outfield test task outfield processing results
实验结果表明,基于动态门限的野值剔除方法能同时判别孤立型野值和斑点型野值,检测率最高,能达到80%以上,同时虚警率最低。3种方法中,固定门限的野值判别方法检测率最低,灵活性最差,检测效果完全依赖于人为设定的先验标准差。无影响函数的野值判别由于采用式(2)计算样本标准差,其不加分辨地依赖每一个样本点,当滑动窗口内有连续多个异常值,估计得到样本标准差大大偏离正常点的实际方差,漏检较多野值点。虚警率的对比中,由于对正常值和异常值进行区分,即便多个点被划分为异常点,本文中方法仍可利用正常点估计样本方差,门限及时得到动态调整,固定门限的方法和无影响函数的方法的估计结果不能根据数据特点实现动态调整,导致容易存在虚警和误判现象。
3.2 插值处理算法
实验基于海军某靶场观测站的实际外场试验任务,主控软件接收来自中心机的20 Hz引导数据,进行坐标转换,实时插值将100 Hz数据发送给机上跟踪器。取L=4,设定阈值threshold=0.2,设定常量increment=0.000 5。
对于出现轻微卡顿点的某次试验记录数据,以方位角为例,外引导接收数据与实时插值数据如图5所示。
图5 轻微卡顿点的插值平滑结果
Fig.5 The results of azimuth angle interpolation for slightly stuck points
图中红色点为本文中方法得到的插值数据,黑色点为原外引导接收值,插值数据能够很好的体现数据的整体趋势,依然保持平滑连贯。无卡顿或者轻微卡顿情况下,此时算法判断2次插值间可以保持连贯,因此直接采用线性最小二乘法的输出作为当前次插值的结果。
某次外引导出现严重卡顿的试验任务,分别运用本文中的方法、线性最小二乘法与牛顿插值法进行处理,以方位角为例,严重卡顿处的处理结果对比如图6所示。
图6 插值处理结果对比
Fig.6 Comparison of interpolation for stuckpoints
图6中(b)、(c)蓝色点分别为线性最小二乘法与牛顿插值法的计算结果,红色点为本文中方法插值结果。由于算法自适应判断插值点是否连贯,即便经纬仪按照插值结果运动缓慢,每一个插值点也能在上一插值点的基础上按照趋势继续增加或减少,不会引起光电经纬仪反向转动、频繁启停,每一次产生的五点插值数据都与前面的插值数据平稳衔接。
进一步分析插值数据点处的角速度,角速度变化情况,当插值数据各点所在处的斜率过渡越平缓,则角速度变化量越接近0,角速度、角速度变化量的绝对值分别记为Ki、ΔKi
(16)
ΔKi=|Ki-Ki-1|
(17)
此次试验任务中3种方法的方位角插值数据点ΔKi之和,如表3所示。
表3 插值数据的ΔKi之和对比
Table 3 Comparison of the sum of ΔKi of interpolated data points
插值方法线性最小二乘牛顿插值本文方法ΔKi和79.040 041.440 022.829 1
可以看出,本文中的方法插值数据点的角速度变化量明显更小,变化最为平缓,更有利于保护伺服系统。
4 结论
研究了靶场光电经纬仪外引导数据的实时平滑算法,算法包括野值处理与插值处理。
1) 基于动态门限的野值处理算法,利用影响函数得到样本方差的计算公式,实现了更准确的野值判别,解决了常规野值判别方法判别门限设置不准、虚警率高的问题,检测率平均在80%以上,优于传统方法。
2) 基于自适应插值的处理算法,自适应地判断数据连贯性,根据卡顿程度采用不同策略,能够同时适应不同卡顿程度的情况,得到的插值引导数据无抖动与不连续现象,获得了较好的平滑效果。
以上算法已成功应用于海军某靶场测控平台,满足靶场光电设备对于弹道测量数据处理的实时性、准确性、平滑性的要求。
[1] BINGHUA H,HENG W,HONGLI H.A new method of trajectory accurate measurement by single photoelectric theodolite[C]//2020 Chinese Automation Congress (CAC).IEEE,2020:4939-4943.
[2] REN Y,ZOU Y,NAN X.Application of large shipborne theodolite in space target measurement[C]//17th International Conference on Optical Communications and Networks (ICOCN2018).SPIE,2019,11048:495-498.
[3] CHEN Y,ZHANG Z,ZHOU X,et al.Design and implementation of real-time intersection simulation for optoelectronic equipment[C]//2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC).IEEE,2019:1465-1469.
[4] 张增继,李俊. 低空监视系统中雷达引导光学跟踪仪的数据融合设计与实现[J].信息通信,2014(11):50-52.ZHANG Zengji,LI Jun.Design and implementation of the radar guiding opto-electronic tracker data fusion in the low-altitude surveillance systems[J].Information &Communications,2014(11):50-52.
[5] HU C,LIU Q,Li Z,et al.Research on multi-parameter tracking effect evaluation system based on photoelectric theodolite[C]//2022 5th International Conference on Data Science and Information Technology (DSIT).IEEE,2022:1-5.
[6] RONGZHEN Z,HAIBO Z,ZHAOHUI W,et al.Research status of video image interpretation technology for photoelectric measurement[C]//2020 IEEE International Conference on Information Technology,Big Data and Artificial Intelligence (ICIBA).IEEE,2020:752-756.
[7] 李霁,李桂芝.多源光测信息融合跟踪方法及应用[J].电光与控制,2023,30(1):82-86.LI Ji,LI Guizhi.Application and measurement of multi-source optical information fusion tracking[J].Electronics Optics &Control,2023,30(1):82-86.
[8] HU C,LIU Q,LI Z,et al.Research on multi-parameter tracking effect evaluation system based on photoelectric theodolite[C]//2022 5th International Conference on Data Science and Information Technology (DSIT).IEEE,2022:1-5.
[9] LIU C,LEI H,ZHANG H,et al.Design and implementation of practical simulation training system for photoelectric theodolite[C]//2022 2nd International Conference on Algorithms,High Performance Computing and Artificial Intelligence (AHPCAI).IEEE,2022:403-407.
[10] 战杰.一种外弹道测量数据的斑点型野值剔除方法[J].航天控制,2016,34(1):75-77,83.ZHAN Jie.A new method of the spotted outliers elimination for exterior ballistic measurement data[J].Aerospace Control,2016,34(1):75-77,83.
[11] 唐自力,周媛媛,周铁军,等.光电经纬仪多数据源融合控制策略[J].电光与控制,2018,25(10):43-46.TANG Zili,ZHOU Yuanyuan,ZHOU Tiejun,et a1.Multi-source data fusion control strategy for photoelectric theodolite[J].Electronics Optics&Control,2018,25(10):43-46.
[12] 李红军,吕绍杰,张永华,等.基于模板滑窗处理测量数据中野值的方法[J].弹箭与制导学报,2020,199(4):135-137,141.LI Hongjun,LYU Shaojie,ZHANG Yonghua, et al.A method of processing outliers in measurement data based on template sliding window[J].Journal of Projectiles,Rockets,Missiles and Guidance,2020,199(4):135-137,141.
[13] 王正明,易东云.测量数据建模与参数估计[M].长沙:国防科技大学出版社,1996.WANG Zhengming,YI Dongyun.Measurement data modeling and parameter estimation[M].Changsha:NUDT Press,1996.
[14] 秦晓珊,张峰,万华,等.雷达探测数据野值剔除方法[J].兵工自动化,2022,41(1):25-29.QIN Xiaoshan,ZHANG feng,WAN Hua,et al.Method for removing outliers from radar detection data[J].Ordnance Industry Automation,2022,41(1):25-29.
[15] 韩先平.基于M估计的外弹道数据小波阈值去噪方法[J].电子测量技术,2019,42(15):18-23.HAN Xianping.Wavelet threshold de-nosing method based on M-estimationfor the external ballistic data[J].Electronic Measurement Technology,2019,42(15):18-23.
[16] 杨军,张东.弹道数据野值灰色自适应检测与修正[J].舰船电子工程,2019,39(10):196-199.YANG Jun,ZHANG Dong.Grey adaptive detection and correction of outliers in ballistic data[J].Ship Electronic Engineering,2019,39(10):196-199.
[17] YANG H,GAO H.Study on time registration method for photoelectric theodolite data fusion[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation.IEEE,2012:3137-3139.
[18] 张兴国,韩涛,李靖.舰载环境下光电经纬仪的引导与实现[J].光电工程,2017,44(5):511-515.ZHANG Xingguo,HAN Tao,LI Jing.Guidance and implementation of photoelectric theodolite in shipborne environment[J].Opto-Electronic Engineering,2017,44(5):511-515.
[19] XU Y,LONG Z,PAN W,et al.Low-cost sensor outlier detection framework for on-line monitoring of particle pollutants in multiple scenarios[J].Environmental Science and Pollution Research,2021:1-18.
[20] LI H,MEDINA D,VILA-VALLS J,et al.Robust variational-based Kalman filter for outlier rejection with correlated measurements[J].IEEE Transactions on Signal Processing,2020(99):1-1.
[21] J
NTSCHI L.A test detecting the outliers for continuous distributions based on the cumulative distribution function of the data being tested[J].Symmetry,2019,11(6):835.
[22] 朱红运,苗岩松,庞建国.基于卡尔曼滤波的遥测数据野值剔除方法[J].航天返回与遥感,2021,42(4):137-143.ZHU Hongyun,MIAO Yansong.PANG Jianguo.An outliers elimination method of telemetry data based on Kalman filter[J].Spacecraft Recovery &Remote Sensing,2021,42(4):137-143.
[23] DAI X W,ZHAO S Y,WU Z J.Odd-even extraction method of the continuous outliers elimination of trajectory data[C]//2019 6th International Conference on Systems and Informatics (ICSAI).2019.
[24] YANG D,DU P,ZHONG M,et al.A Real-time fusion method of external trajectory measurement data based on variable difference method[C]//2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC).IEEE,2020,9:574-577.
[25] MEYER G P.An alternative probabilistic interpretation of the huber loss[C]//Proceedings of the ieee/cvf conference on computer vision and pattern recognition.2021:5261-5269.
[26] OGASAWARA H.A non-recursive formula for various moments of the multivariate normal distribution with sectional truncation[J].Journal of Multivariate Analysis,2021,183:104729.
[27] 黄博深,肖云.重力卫星轨道数据插值方法适应性研究[J].甘肃科学学报,2022,34(3):1-7.HUANG Boshen,XIAO Yun.Study on the adaptability of gravity satellite orbit data interpolation method[J]Journal of Gansu Sciences,2022,34(3):1-7.
[28] YANG D,DU P,ZHONG M,et al.A real-time fusion method of external trajectory measurement data based on variable difference method[C]//2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC).IEEE,2020,9:574-577.
[29] 谢勇.光电经纬仪主控软件的研制[D].成都:电子科技大学,2012.XIE Yong.Development of main control software for photoelectric theodolite[D].Chengdu:University of Electronic Science and Technology of China,2012.
[30] 米阳,刘华军,张鹏.光电经纬仪靶场精度检测数据误差分析[J].光机电信息,2010,27(10):50-54.MI Yang,LIU Huajun,ZHANG Peng.Data error analysis for precision detection of opto-electronic theodolites in shooting range[J].OME Information,2010,27(10):50-54.