0 引言
齿轮作为机械设备中的关键零件被广泛应用于各种传动系统,其健康状况往往是影响大型设备安全工作的重要因素,然而,在齿轮的工作过程中,往往会受到极端环境的影响发生磨损裂纹等故障,在继续啮合过程中导致齿轮失效,进而引发安全和经济事故。为了时刻监测齿轮的运行状态是否正常,以及更精确的提取出代表该故障下的特征信息并调查失效机理,对于减小机械设备重大损失至关重要。
一般而言,齿轮工作在噪声环境中,这给故障信息提取带来很大挑战。由于振动信号中会包含着各种运行状态丰富的信息,因此,利用振动信号来诊断齿轮故障一直是故障诊断领域研究的主要方向[1-2]。经验模态分解(EMD)是一种常见的自适应信号处理和特征提取方法,它弥补了傅里叶变换不能分析时变信号的缺陷,被广泛运用到故障诊断的研究中。刘剑生等[3]采用EMD方法提取时域信号IMF分量,以该分量下能量特征参数输入BP神经网络,结果上训练误差和迭代次数方面有明显的改善。在此基础上,CEEMDAN通过将自适应噪声模态分量添加到EMD分解的每阶段,并且对每阶段的模态分量进行平均,有效地解决了模态混叠和传统分解方法无法有效分解非平稳非线性振动信号的问题。蔡超志等[4]使用CEEMDAN将自适应小波做分解和重组处理之后,提取一维卷积神经网络的基本数字特征对齿轮箱进行故障诊断,可以在高噪声的环境下依然取得较高训练精度。目前,用于齿轮故障诊断的人工智能算法主要有卷积神经网络、支持向量机(SVM)等。金江涛等[5]将变分模态分解与能量熵结合,在此基础上构建多模态特征矩阵,借助灰狼算法优化支持向量机参数,最后采用轴承实验数据验证该模型的有效性。以上在深度学习的研究对故障诊断领域的发展起到一定的作用,但仍然存在一些不足,例如,对先验知识的依赖性大,复杂工况下准确率低。自适应神经模糊推理系统是将神经网络的学习方式和模糊系统的语言推理能力充分结合,这样汲取两者的长处后,在补偿双方局限性的同时,学习能力更强,收敛速度更快、诊断精度更高。近年来被广泛应用于预测研究模式识别等领域。Mohsen Motahari-Nezhad等[6]分别使用PCA和FDA计算出45个频域特征的主成分,用ANFIS对2种方法下的主成分对健康和缺陷分类,在测功机高速球轴承的故障诊断上获得很高的准确性。
使用离散小波变换将心音信号分解为几个子带,并通过香农熵对其进行量化。最后,利用ANFIS对心音信号进行分类,完成对心脏瓣膜疾病的检测。
受上述文献启发,本研究中结合CEEMDAN、核主成分分析和能量熵,将ANFIS模型应用于齿轮的故障诊断中。通过自适应噪声完备经验模式分解振动信号获取各尺度下IMF分量,提取各分量时频域指标能量熵与传统时域信号统计指标作为补充特征来提高深度学习模型的泛化能力,将其经过降维处理后作为特征向量输入到ANFIS模型中,进行故障的分类识别和诊断,并验证了该方法的有效性。
1 基于CEEMDAN的能量熵提取
1.1 CEEMDAN
为了解决传统分解方法对非平稳非线性信号处理的局限性,自适应噪声完备经验模式分解(CEEMDAN)[8] 在EMD的基础之上,在振动信号中添加有限次数正负序列的高斯白噪声,多次叠加求平均值可以抵消噪声来辅助分解。有效解决了EMD中模态混叠及EEMD法由于参数选择出现过多虚假分量的问题。CEEMDAN算法步骤如下:
步骤1：对原始振动信号x(n)加入噪声可得x(n)+e0ωi(n),进行一次EMD分解后,取其平均值IMF1为
(1)
其中,ωi(i=1,2,…,i)是满足标准正态分布的高斯白噪声。
步骤2：计算出第1个残余分量
r1(n)=x(n)-IMF1(n)
(2)
步骤3：第1个残余分量加入白噪声,此时信号为 r1(n)+e1E1(ωi(n)),其中,e1为每个阶段的信噪比,且e1=ω1std(r(1))。对此时的信号继续做EMD分解可得IMF2(n)
(3)
步骤4：计算当k=2,3,…,k时的残余分量rk(n)
rk(n)=rk-1(n)-IMFk(n)
(4)
步骤5：计算rk(n)+ekEk(ωi(n)),i=1,2,…,i,做EMD分解后可得到第k+1个模态分量
(5)
步骤6：重复上述步骤4—步骤6,直到残余分量单调,即极值点个数小于3时结束分解,最后得到残余分量
(6)
步骤7：此时原始信号x(n)可表示为
(7)
1.2 CEEMDAN能量熵
在描述一个系统时,经常会借助熵的概念来表征该系统的平均不确定程度。由于齿轮在正常运行或者出现故障时,会导致该状态下振动信号所包含的频率成分有区别,相对应地,它频率成分所对应的能量分布也会随之改变。故能量熵适用于非线性数据的特征提取。由于CEEMDAN所分解出的IMF包含从高频到低频分布的唯一频带,因此想要定量的展现齿轮振动信号能量分布与故障状态的变化关系,本文中提出基于CEEMDAN能量熵的方法来表述信号能量大小。具体原理如下:
1) 对预处理后的重构信号做CEEMDAN分解,可得n个IMF,IMF1,IMF2,…,IMFn;
2) 计算n阶IMF分量的能量值,E1,E2,…,En;
(8)
(9)
其中:Ei表示第i个元素的能量;xik表示各阶IMF;E表示总能量。
3) 相应地,CEEMDAN能量熵可定义为
(10)
式(10)中:pi表示第i各IMF分量的能量占整个能量信号的比重;pi=Ei/E(i=1,2,…,n)。
2 自适应神经模糊推理故障诊断方法
2.1 ANFIS
ANFIS[9]是一种将模糊逻辑和神经元网络有机结合的新型模糊推理系统结构,可实现对不精准模型的推理并且在不确定系统中获得结论。与传统的BP神经网络相比较,该模型的自学习能力、鲁棒性和自适应性更强,可以以任意精度逼近非线性函数[10],共分2步过程:首先基于模糊if-then规则的形式以及规定的输入-输出数据对来构建输入-输出映射;其次ANFIS分别使用反向传播梯度下降和最小二乘法来调节隶属函数和其他相关参数,以此调整整个系统的准确度。通过两者的结合使得该系统同时具有模糊推理系统的可解释性以及自适应网络的学习能力,减少了人类经验的依赖,让结果更加客观。充分发挥各自优点的同时也弥补了对方缺点。其中模糊神经网络原理[11]如图1所示。
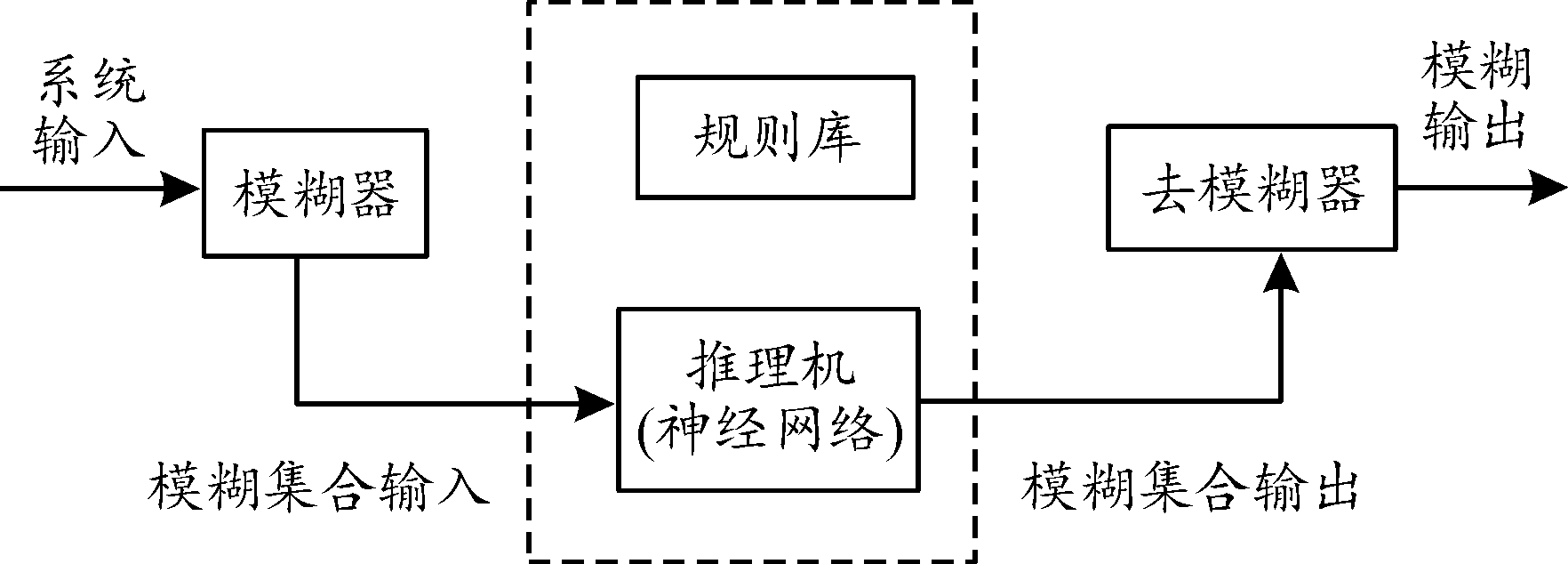
图1 模糊神经网络原理框图
Fig.1 Schematic diagram of fuzzy neural network
所采用的ANFIS系统是以Takagi-Sugeno型模糊规则为基础,是由x和y两个输入,一个输出f所组成的5层网络结构,包含以下2条规则:
规则1:if x=A1y=B1, then f1=p1x+q1y+r1
规则2:if x=A2y=B2, then f2=p2x+q2y+r2
其中:Ai、Bi是规则i所确定的模糊集(语言标签);p1、q1、r1是规则1的结论参数,p2、q2、r2是规则2的结论参数; fi为规则i对应的输出结果。采用
来表示第i层第j个节点的输出,那么一阶T-S模糊推理系统的ANFIS网络结构如图2所示。
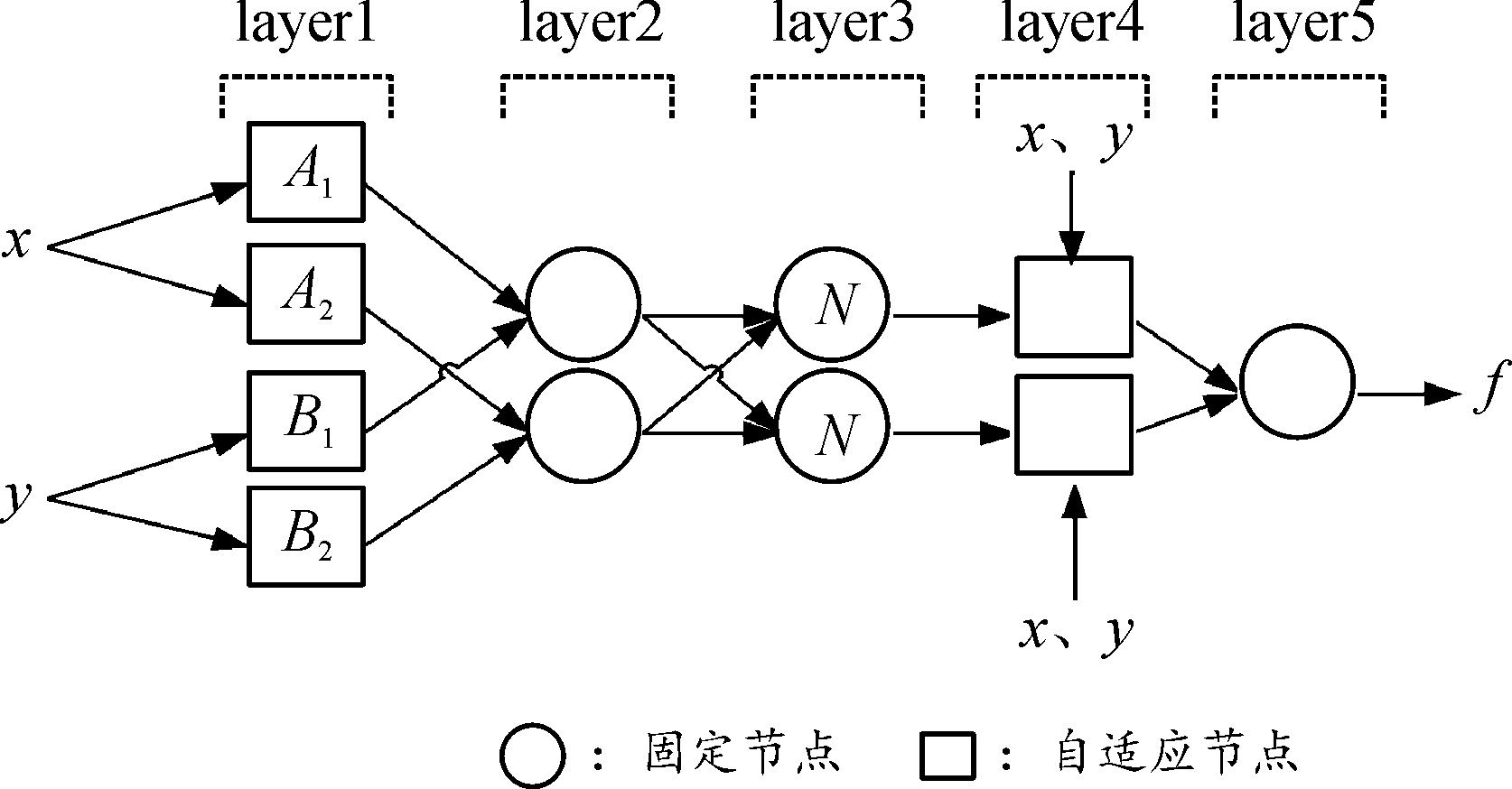
图2 ANFIS结构框图
Fig.2 ANFIS structure diagram
图2中,方形节点表示有参数的自适应节点;圆形节点表示无参数的固定节点。
Layer1:输入层。由i个具有节点函数的方形节点组成,它对输入参数做模糊处理,使之转换成在不同模糊集下[0,1]内的隶属度,通常用mu表示。该值越大则称被满足的程度越大。
(11)
(12)
其中:i表示节点;x、y表示节点i的输入变量;
表示第1层i节点对应的隶属度值; μAi(x)、 μBi(y)分别表示x、y的隶属函数,一般来说,高斯隶属度和钟形隶属度具有光滑性和简洁性的特点,并被广泛应用于模糊集。钟形隶属度对于非线性系统来说非常重要,并且比高斯隶属度更好。因此在研究中一般为钟形函数
(13)
其中,ai、bi、ci是if-then规则前提部分中隶属函数的参数集,进而改变隶属函数的形状,被称为前提参数或非线性参数。
Layer2:模糊集的运算。每个节点代表一个规则,计算每个规则的适合度,它是由不同模糊集的隶属度相乘来获得的。
(14)
Layer3:触发强度归一化。计算出该规则在整个规则库中使用到第i个规则的程度
(15)
Layer4:计算每条规则的输出
(16)
其中:
是从上一层传过来的触发强度;pi、qi、ri是结论参数或结果参数。
Layer5:输出层。该层主要是一个去模糊化的过程,这是每条规则的加权平均,得到ANFIS单变量确切输出。
(17)
在上述ANFIS结构中,是由第1层和第4层2个自适应层以及第2、3、5层3个固定层组成,模型的参数是需要不断调整的。对于前提参数来说,使用的是反向传播算法训练,而对于结论参数来说则采用线性最小二乘估计算法来调整[12]。在训练的每一次迭代过程中,首先固定前提参数不变,将输入信号沿网络正向传递第4层,采用最小二乘估计算法调节结论参数;然后,信号继续沿网络正向传递直到输出层。此后,将获得的误差信号沿网络反向传播,从而可反向调节前提参数。通过该训练过程重复调整网络参数,直到输出符合收敛条件,这大大提高了训练效率与准确率。
2.2 基于CEEMDAN能量熵和ANFIS的故障诊断模型
本研究中结合CEEMDAN对信号分解的优势以及能量熵在不同状态下的差异,提出了一种基于ANFIS模型的齿轮故障诊断方法。首先将预处理后的振动信号做CEEMDAN分解,得到若干IMF分量,得到该信号的时频域特征,再计算出该齿轮信号的平均值等11个时域指标,经过核主元分析(KPCA)降维得到齿轮信号的时域特征,把降维后的所有特征构成故障特征矩阵,作为ANFIS模型的输入,进而实现故障的分类识别。其故障诊断流程图如图3所示,具体步骤如下:
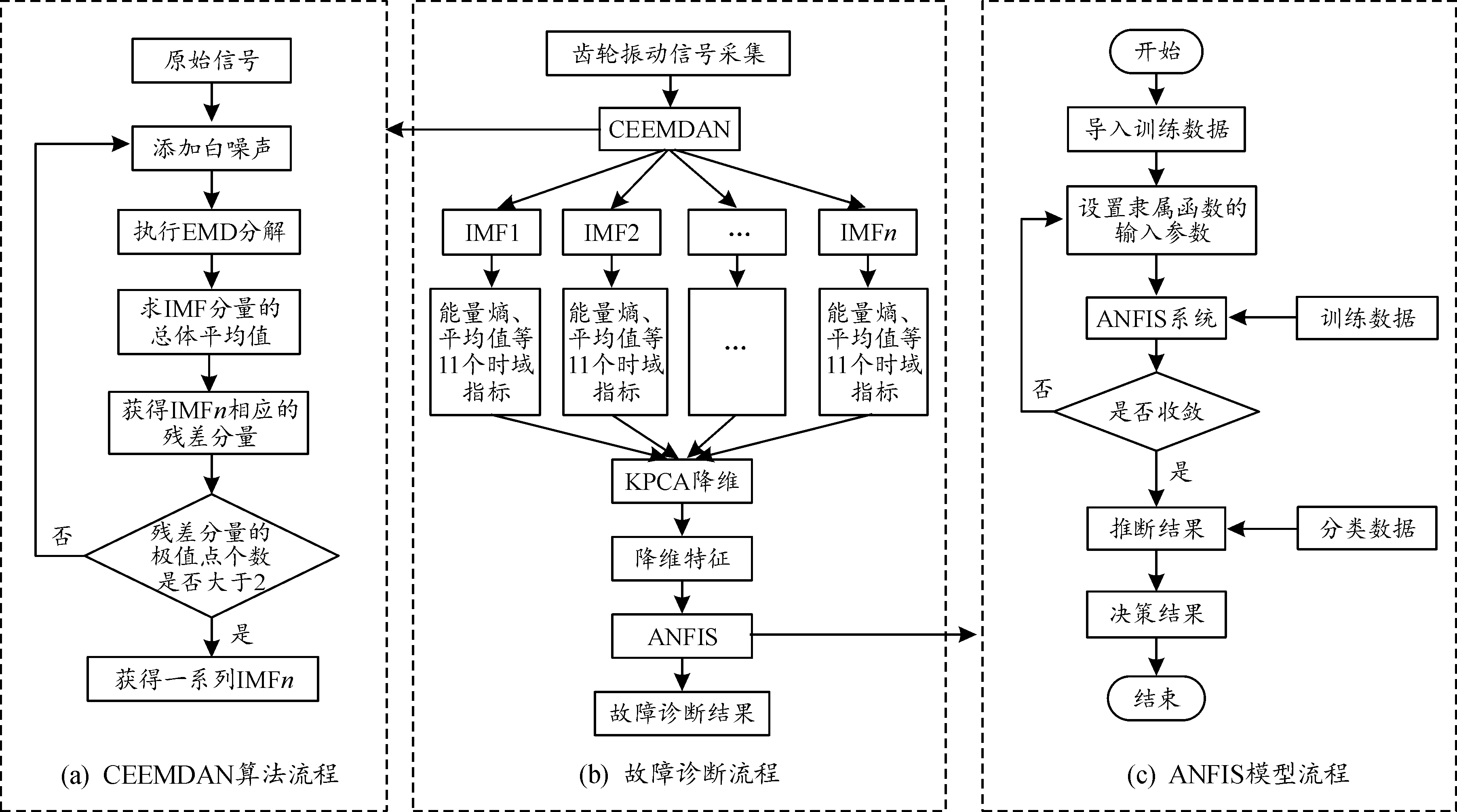
图3 故障诊断整体流程框图
Fig.3 Overall flowchart of fault diagnosis
步骤1：振动信号的采集,以20 kHz的采样频率分别采样齿轮在正常状态、缺齿、断齿、均匀磨损以及裂纹故障状态下的振动信号,以此获得各状态下的振动数据样本,经过去噪处理后选取不同状态的部分数据作为样本训练集;
步骤2：数据预处理,使用CEEMDAN算法对样本进行分解,得到5种状态下的若干本征模态分量;
步骤3：故障特征提取,计算各模态分量的能量熵作为齿轮信号的时频域特征;计算齿轮信号的11个统计时域指标,经过KPCA降维得到该样本的时域特征;
步骤4：将步骤3所提取的信号时频域特征、时域特征共同构成齿轮信号的分类特征矩阵向量;
步骤5：将步骤4所构建的特征向量作为ANFIS模型的输入,从而识别齿轮的工作状态和故障类型。
3 实验结果与分析
3.1 实验设备和数据采集
实验分别采集正常、故障齿轮振动数据来验证该模型的有效性,设置采样频率为20 kHz,充分考虑到齿轮的复杂工作环境,以转速2 800 r/min模拟了齿轮在正常、缺齿、断齿、磨损、裂纹5种状态下,无负载的工作情况。如图4所示,用xxx型数字采集设备在X、Y、Z 3个方向上分别采集振动信号,将其分成500组信号样本,每组520个数据样本点。按8:2的比例划分成400个样本作为训练集,100个样本作为测试集。其中,实验台故障齿轮如图5所示。
图4 实验装置平台
Fig.4 Experimental device platform
图5 故障齿轮
Fig.5 Faulty gear
3.2 自适应模糊推理系统故障诊断
每种故障数据取20组作为训练样本,共100组。对这些样本数据分别求取11个时域特征指标:平均值、标准差、偏度、峭度、最大值、最小值、峰峰值、均方根、振幅因数、波形因数、冲击因数。以及做CEEMDAN分解后求得每组数据的时频域指标能量熵,则每种故障下共有20×12个特征值。以断齿故障为例,该故障状态下获得的部分特征值如表1所示。
表1 断齿故障部分特征值
Table 1 Partial characteristic values of broken teeth fault
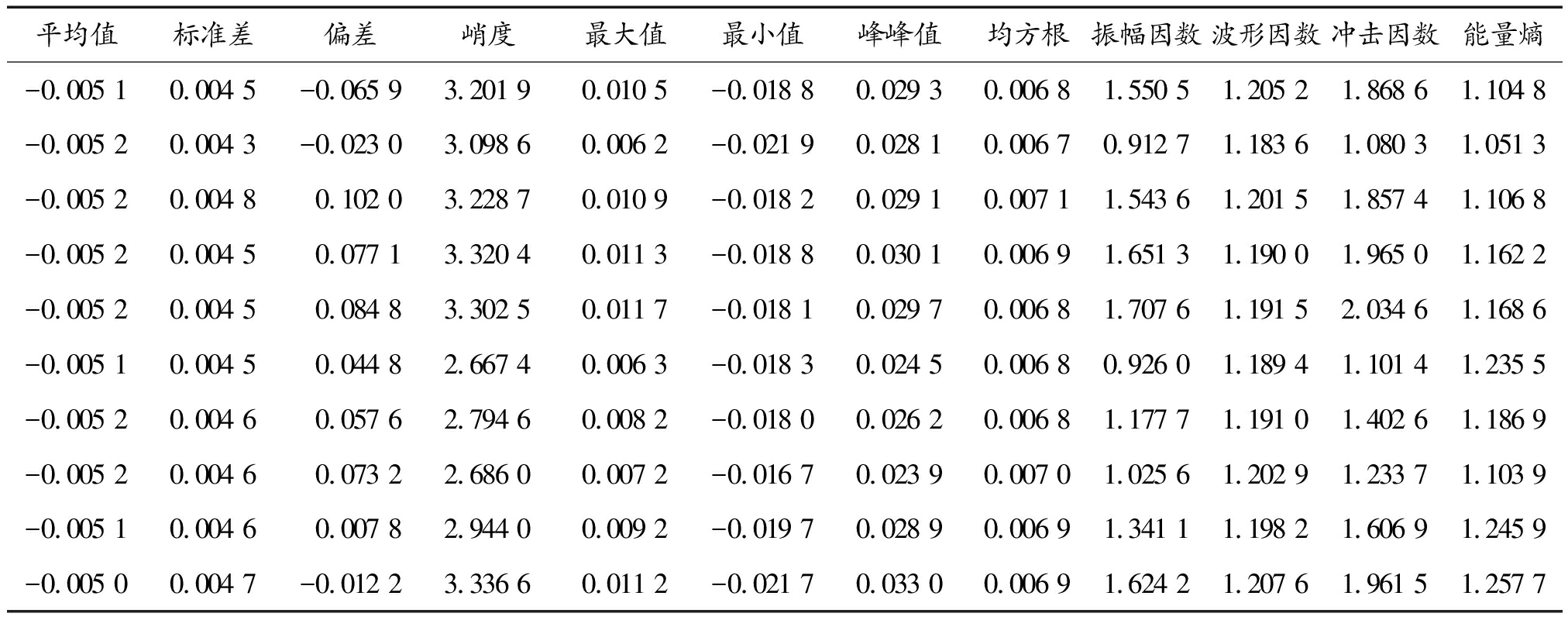
平均值标准差偏差峭度最大值最小值峰峰值均方根振幅因数波形因数冲击因数能量熵-0.005 10.004 5-0.065 93.201 90.010 5-0.018 80.029 30.006 81.550 51.205 21.868 61.104 8-0.005 20.004 3-0.023 03.098 60.006 2-0.021 90.028 10.006 70.912 71.183 61.080 31.051 3-0.005 20.004 80.102 03.228 70.010 9-0.018 20.029 10.007 11.543 61.201 51.857 41.106 8-0.005 20.004 50.077 13.320 40.011 3-0.018 80.030 10.006 91.651 31.190 01.965 01.162 2-0.005 20.004 50.084 83.302 50.011 7-0.018 10.029 70.006 81.707 61.191 52.034 61.168 6-0.005 10.004 50.044 82.667 40.006 3-0.018 30.024 50.006 80.926 01.189 41.101 41.235 5-0.005 20.004 60.057 62.794 60.008 2-0.018 00.026 20.006 81.177 71.191 01.402 61.186 9-0.005 20.004 60.073 22.686 00.007 2-0.016 70.023 90.007 01.025 61.202 91.233 71.103 9-0.005 10.004 60.007 82.944 00.009 2-0.019 70.028 90.006 91.341 11.198 21.606 91.245 9-0.005 00.004 7-0.012 23.336 60.011 2-0.021 70.033 00.006 91.624 21.207 61.961 51.257 7
从表1可以看到,仅一种故障的10组数据的特征信息量很大,高维的特征向量会使这些时域指标存在信息冗余,增加计算的复杂性,诊断时间变长。因此,为了提高运行效率,本研究中采用核主成分分析实现数据的非线性降维,它减少了数据的维数,同时将数据集中贡献最大的特征保留下来,结果如图6所示。
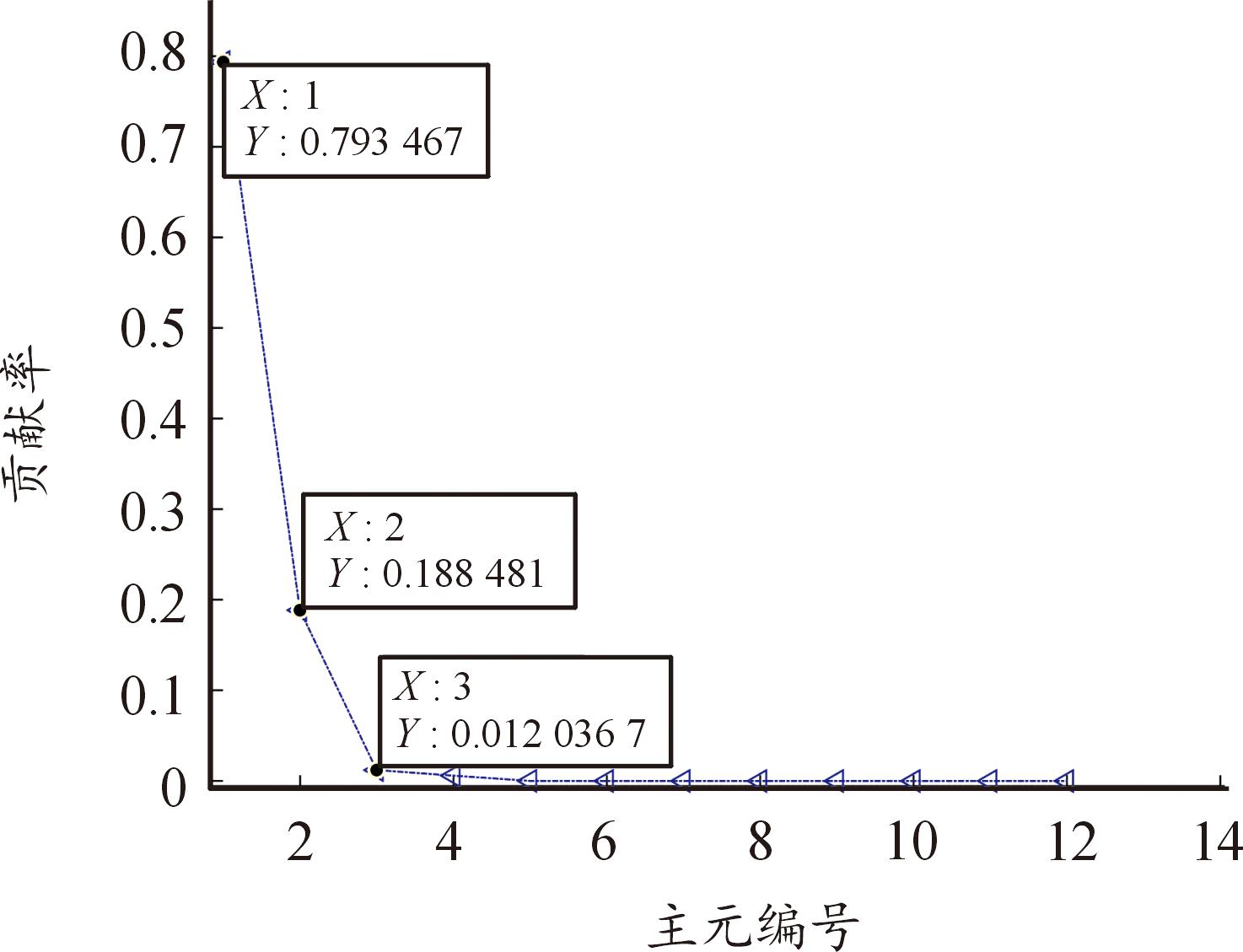
图6 特征主元贡献率
Fig.6 Contribution rate of feature principal components
由图6可知,前3个主元的累计贡献率可达99.4%,因此选前3个主元作为最终特征。缩减后的特征向量组成了故障诊断系统的数据库。将这3个主元特征排列,可以得到100×3个特征值,每个样本3个特征值组成可代表该状态的特征向量,即5种状态下共有100个特征向量。把这100个特征向量作为模型输入,输入到ANFIS进行训练进一步识别和诊断齿轮状态。输出标签分别标识为:正常状态输出1,断齿故障输出2,磨损故障输出3,裂纹故障输出4,缺齿故障输出5。
网络参数训练如下:输入节点为3个,模糊集的个数为4个,规则节点数量为8,步长0.1,训练次数为100次。当上述测试样本用作输入时,训练样本自适应地调整ANFIS模型参数和隶属函数后使得ANFIS模型的输出,如果结果在区间[0.5,1.5]内,则应为正常状态;如果输出在区间[1.5,2.5]内,则应为断齿故障;如果输出在区间[2.5,3.5]内,则应为磨损故障;如果输出在区间[3.5,4.5]内,则应为齿根有裂纹的齿轮。如果输出超过[0.5,5.5]的范围,则无法确定该齿轮的状态。
训练后的ANFIS模型在各种故障状态下的测试结果如图7显示。其中,“*”代表实际输出结果,“—”代表模型预测标准输出结果。在该模型下测试结果的绝对误差较小,每种状态都可以得到近乎100%的识别率,表明ANFIS模型在训练后的性能具有更好的性能。图8显示了在该训练过程中RMSE的变化,可以看到在训练到约25步时已经收敛,训练误差收敛为0.000 772 29。
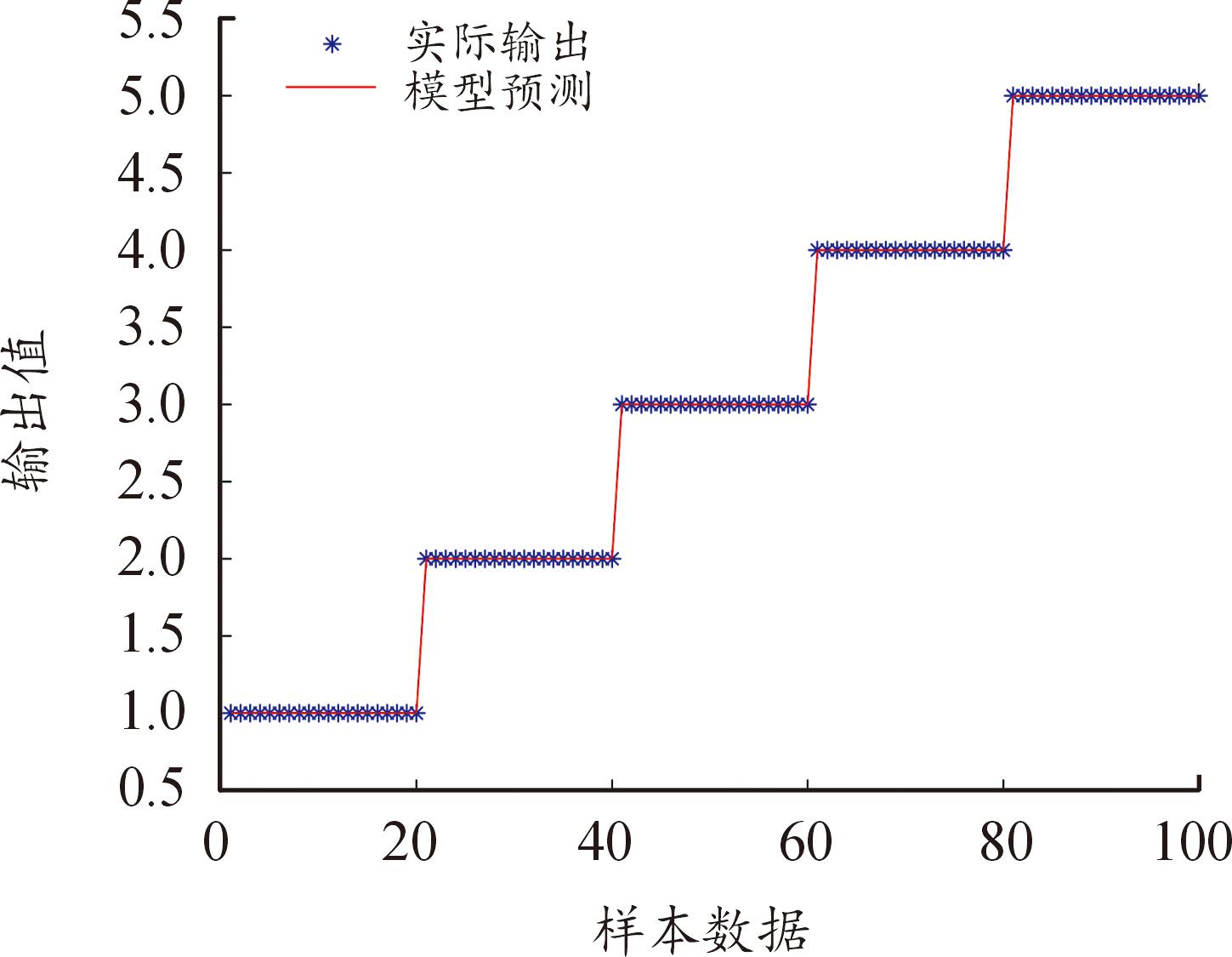
图7 ANFIS样本测试结果
Fig.7 ANFIS sample test results
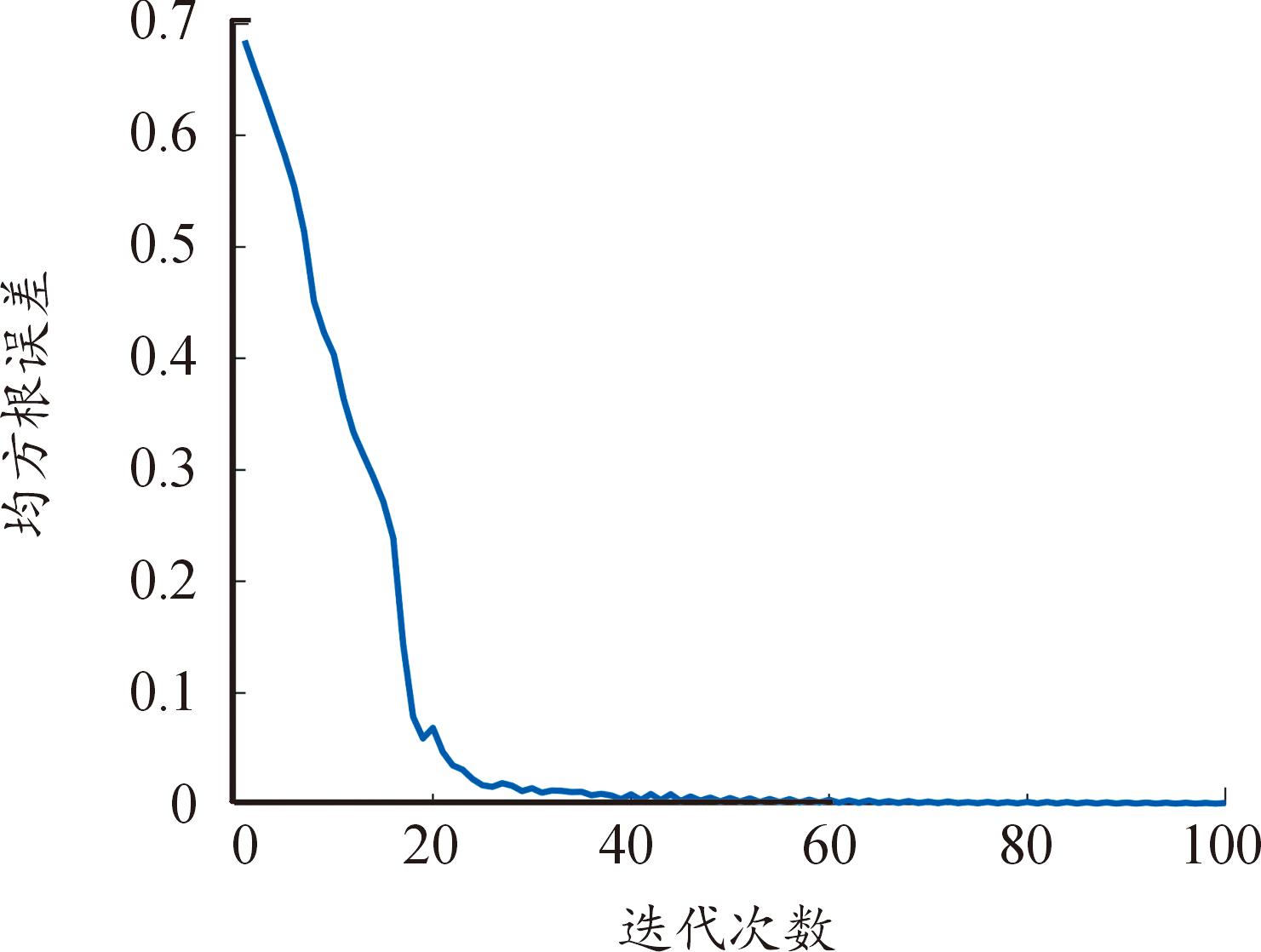
图8 RMSE曲线
Fig.8 RMSE curve
为了更好地展现ANFIS在故障诊断中的良好识别效果,选择使用BP神经网络进行对比分析,其参数设置如下:BP神经网络网络结构中输入层神经元个数为5个,隐含层神经元个数为11个,输出层神经元个数为10个。2种方法的诊断运行结果对比如表2所示。
表2 2种故障诊断法比较结果
Table 2 Comparison of two fault diagnosis methods
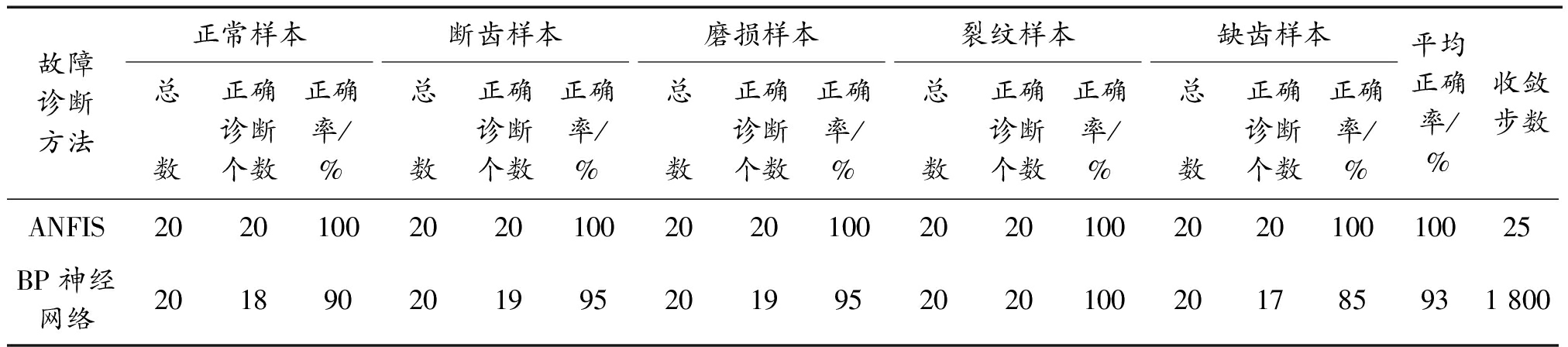
故障诊断方法正常样本总数正确诊断个数正确率/%断齿样本总数正确诊断个数正确率/%磨损样本总数正确诊断个数正确率/%裂纹样本总数正确诊断个数正确率/%缺齿样本总数正确诊断个数正确率/%平均正确率/%收敛步数ANFIS2020100202010020201002020100202010010025BP神经网络2018902019952019952020100201785931 800
从表2中可以看出,本文中的自适应神经模糊推理系统故障诊断方法,吸取模糊理论和神经网络两者的优点,使获得诊断结果的收敛速度很快。在故障齿轮的识别检测中,与使用BP神经网络故障诊断方法相比,诊断精度和收敛速度上有很大的优势。
4 结论
针对齿轮断齿、磨损、裂纹、缺齿故障出现噪声污染严重,故障特征信息提取困难问题,提出了基于能量熵和ANFIS相融合的齿轮故障诊断识别方法。并从数据获取、提取故障特征信息和故障分类诊断3个方面进行了研讨,最后采用实验对比验证了该模型的有效性和准确性。主要结论如下:
1) 由于齿轮工作在高噪声环境下,特征提取较为困难,因此采用提取能量熵的方法,更精准地反映了不同故障状态下的故障信息,更好地避免的噪声对特征的干扰。
2) 采用CEEMDAN方法应用于故障诊断,大大降低了模态混叠问题。获取时频指标能量熵,同时提取11个时域指标作为信息补充,经过核主成分分析降维后作为特征输入,可以在不丢失太多信息的情况下降低维数生成新的指标,大大减轻计算机的工作量。
3) 采用ANFIS模型准确地诊断出各故障类型,将模糊逻辑与神经元有效结合,与BP神经网络相比,诊断精度更高可达100%,收敛速度也极具优势,更加适用于故障齿轮的诊断。
[1] SALAMEH J P,CAUET S,ETIEN E,et al.Gearbox condition monitoring in wind turbines[J].Mechanical Systems and Signal Processing,2018,111(5):251-264.
[2] LUO Y C,CUI L L,ZHANG J Y,et al.Vibration mechanism and improved phenomenological model of planetary gearbox with broken sun gear fault[J].Measurement,2021,178(3):178:193.
[3] 刘剑生,王细洋.基于EMD与BP神经网络的齿轮故障诊断[J].失效分析与预防,2020,15(6):370:392.LIU Jiansheng,WANG Xiyang.Gear fault diagnosis based on emd and bp neural network[J].Failure Analysis and Prevention,2020,15(6):370:392.
[4] 蔡超志,白金鑫,池耀磊,等.基于CEEMDAN自适应小波降噪与卷积神经网络的齿轮箱故障诊断研究[J].机床与液压,2022,50(24):171-180.CAI Chaozhi,BAI Jinxin,CHI Yaolei,et al.Research on gearbox fault diagnosis based on ceemdan adaptive wavelet denoising and convolutional neural network[J].Machine tools and hydraulics,2022,50(24):171-180.
[5] 金江涛,许子非,李春,等.基于VMD能量熵与优化支持向量机的轴承故障诊断[J].计量学报,2021,42(7):898-905.JIN Jiangtao,XU Zifei,LI Chun,et al.Bearing fault diagnosis based on vmd energy entropy and optimized support vector machine[J].Journal of Metrology,2021,42(7):898-905.
[6] NEZHAD M M,JAFARI S M.ANFIS system for prognosis of dynamometer high-speed ball bearing based on frequency domain acoustic emission signals[J].Measurement,Volume,2020,166(6):108-154.
[7]
H.Adaptive neuro-fuzzy inference system for diagnosis of the heart valve diseases using wavelet transform with entropy[J].Neural Computing and Applications,2012,1617-1628.
[8] TORRES M E,CLOLMINAS M A,SCHLOTTHAUER G,et al.A complete ensemble empirical mode decomposition with adaptive noise[C]//Acoustics:2011 IEE International Conference on Acoustic Speech and Signal Processing(ICASSP).[S.l.]:[s.n.],2011:4144-4147.
[9] JANG,J S R.ANFIS:Adaptive network based fuzzy inference system[J].IEEE Transactions on Systems,2 1993(23):1094-1097.
[10] 王生昌,赵永杰,许青杰.基于自适应模糊神经网络的故障诊断方法[J].汽车工程,2006(4):398-409.WANG Shengchang,ZHAO Yongjie,XU Qingjie.A fault diagnosis method based on adaptive fuzzy neural network[J].automotive engineering,2006(4):398-409.
[11] 王志伟,胡瑜,李银伟.基于小波和自适应模糊神经的旋转设备故障诊断[J].华东交通大学学报,2010,27(1):72-77.WANG Zhiwei,HU Yu,LI Yinwei.Fault diagnosis of rotating equipment based on wavelet and adaptive fuzzy neural networks[J].Journal of East China Jiaotong University,2010,27(1):72-77.
[12] 张小娟.自适应神经模糊推理系统(ANFIS)及其仿真[J].电子设计工程,2012,20(5):11-13.ZHANG Xiaojuan.Adaptive neural fuzzy inference system (anfis) and its simulation.[J].Electronic Design Engineering,2012,20(5):11-13.