0 引言
弹丸在外弹道飞行时要受到空气阻力对其作用,常规弹丸在超音速飞行时受到阻力主要由波阻、底阻和摩阻3部分组成,其中前2部分所占比重最大(80%以上),空心弹丸理论上可以消除(或大大减小)波阻和底阻,因而其飞行阻力小,气动特性得以明显改善[1-2]。空心弹丸主要分为内锥形、外锥型和内外锥混合型,只有内锥型空心弹丸能够完全消除波阻和底阻,存速能力强,能够给予目标最大程度地动能打击,而且成本低,易于实现密集火力打击,因而极具研究价值。
目前在空心弹气动特性研究方面,主要以风洞试验和借助CFD数值模拟方法为主。其中风洞试验在传统的气动外形设计方法中较为常见,通常是对不同的设计方案进行一系列风洞试验,并对一系列试验结果进行综合分析,此方法具有较长的设计周期和较低的成本效益[3]。随着计算流体力学不断发展和数值模拟技术的成熟,借助CFD技术进行气动设计已经成为国内外学者研究空心弹的重要手段。陈杨等[4]以12.7 mm口径实心弹和空心弹进行模拟仿真,得出空心弹丸的阻力系数比实心弹丸小很多,并且在外弹道过程中,空心弹丸能够更好的保持飞行速度。杜宏宝等[5]通过对喉道与入口截面积比为0.6的模型仿真研究,得到了内锥型空心弹阻塞现象与入口锥角的关系。赵强等[6]利用Kriging近似模型和NSGA-Ⅱ优化算法等对30 mm空心弹气动外形进行优化,得到了相应的优化外形。张浩等[7]应用Fluent软件仿真空心弹典型设计方案简化模型的空气动力流场,得到了其阻力系数与马赫数的关系。黄振贵等[8]基于雷诺平均方程以及二阶AUSM格式,对不同空心弹气动外形的二维流场以及气动力进行了数值计算,得到了不同外形条件下空心弹的内外流场特性。钱吉胜等[9]通过数值模拟了空心弹表面穿孔与无穿孔条件下的流场参数分布,得出穿孔会使弹丸表面流场分布变得更加复杂,增加新的斜激波与膨胀波系。全鑫等[10]为了研究内锥型空心弹喉径面积之比与阻塞现象发生的关系,利用穷举法对入口锥角12°的空心弹丸计算,得到了不同马赫数下临界喉径面积比不同。罗驭川等[11]对不同马赫数条件下空心弹弹体和弹托的分离过程进行了仿真,得到了弹体阻力整体上呈先减后增,最终达到稳定。此外一些国外学者也对空心弹进行了数值计算[12-14],得到了较为准确的阻力系数及波系结构。
以上对空心弹研究主要集中在外锥型和内外锥混合型,在内锥型空心弹研究方面相对较少,目前学者主要研究单一参数对阻塞现象影响规律,如基于锲角不变,分析阻塞与喉径比关系,确定临界喉径比;或是基于喉径比不变,分析阻塞与锲角关系,确定临界锲角等。而锲角和喉径比在不同马赫数条件下,都是影响空心弹丸阻力特性关键因素需同时考虑。锲角、喉径比和马赫数三者间关系对内锥型空心弹阻力特性影响规律目前暂未见相关公开报道。本文借助计算流体动力学软件Fluent软件对内锥型空心弹模型在不同锲角、不同喉径比和不同马赫数条件下进行仿真分析,结合压力等值线分布云图和数据汇总分析,得出关键参数对阻力特性影响规律,本文的研究可为内锥型空心弹的科学研究和工程应用提供理论参考。
1 数值模型建立
内锥型空心弹丸,主要关注外形参数为锲角和喉径比,为探明锲角和喉径比在不同马赫数条件下与阻力特性之间的关系,通过分别改变锲角θ与喉径比HJB取值的方式进行研究,所述内锥型空心弹模型的基本形状如图1所示。
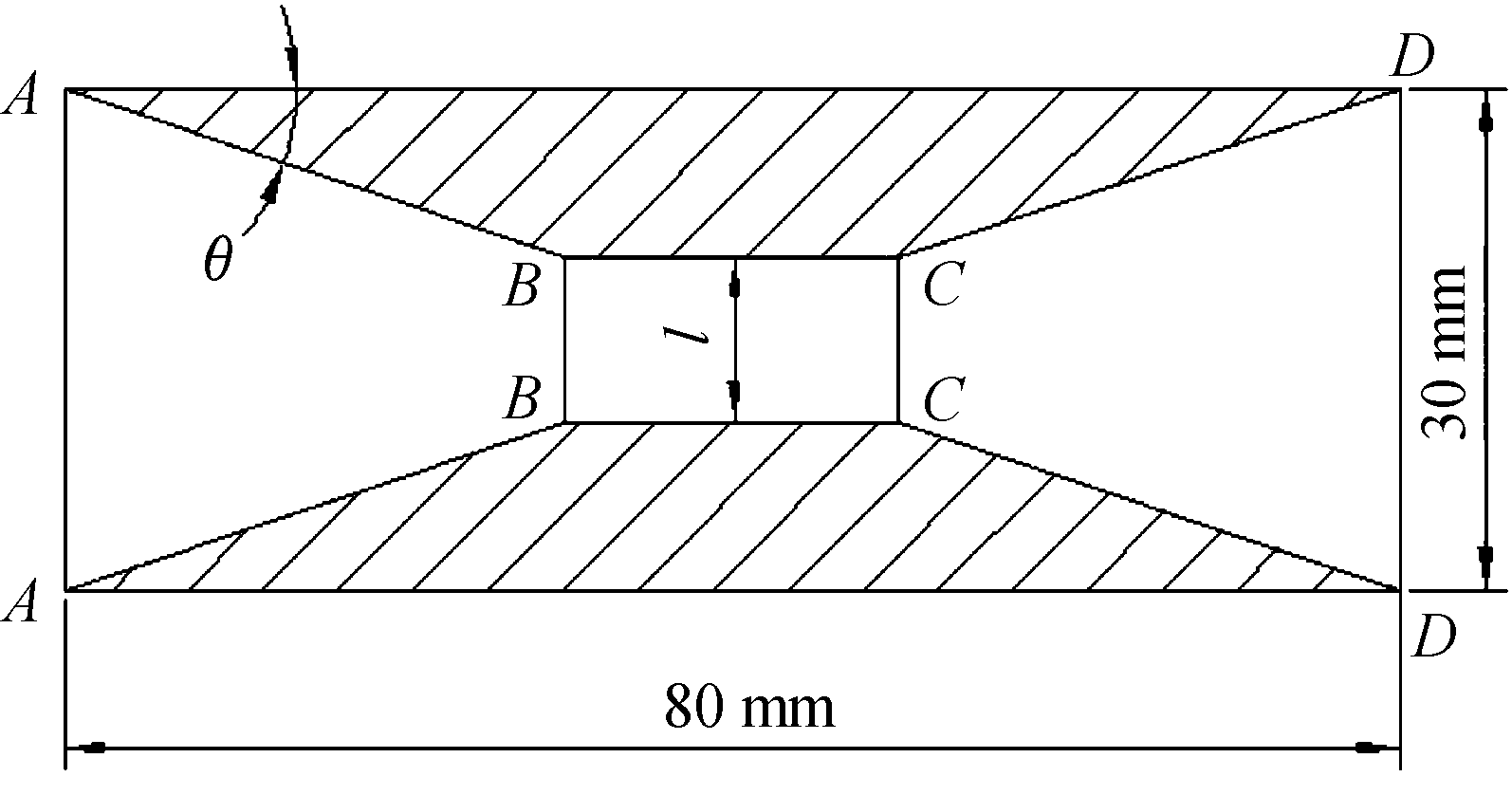
图1 内锥型空心弹模型
Fig.1 Inner cone hollow bullet model
图1中弹丸长度取80 mm,弹丸口径取30 mm,喉道口径取值为l,l通过喉径比HJB取值变化而改变,弹丸前顶点命名为A,喉道前顶点命名为B,喉道后顶点命名为C,弹丸后顶点命名为D。针对此模型,仿真时,使用有限体积法进行求解,其中前处理器对计算域尺寸设置为:长为12.5倍弹长,宽为20倍弹径,采用四边形单元进行网格划分,求解器选用基于密度基的耦合显示算法,湍流模型选择Spalart-Allmaras单方程模型,粘性项采用二阶中心差分格式,对来流采用压力远场(pressure far field)边界条件。由于空气弹相比实心弹在超音速流场甚至是高超音速流场具有良好气动特性,本文仿真流场均为超音速流场,为更好捕捉超音速流场中激波,采用网格自适应加密技术,采用AUSM格式进行激波捕捉[15]。
2 数值计算结果与分析
2.1 流场数值模拟结果与分析
采用穷举法依次对锲角θ分别取20°、30°、40°、50°,喉径比HJB分别取0.2、0.3、0.4、0.5、0.6、0.7、0.8,马赫数取值分别为2.0、2.4、2.8、3.2、3.6进行仿真计算,累计工况达140组,由于工况较多,这里以锲角θ在20°时为例,对空心弹在不同喉径比、不同马赫数工况条件下仿真结果进行分析,压力云图仿真计算结果如图2—图8所示。

图2 θ=20°,HJB=0.2时不同马赫数下压力等值线分布
Fig.2 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.2
从图2中结果可知,在θ=20°,HJB=0.2时,由于喉径比过小,即使随着马赫数增加,弹体在进气道出现阻塞现象并未消除,同时在弹体前出现脱体激波,来流在经过激波面后减速增压,最大压力区基本出现在进气道附近;从图3中可看出在喉径比增加至0.3后,随着马赫数不断增加,在3.6Ma时弹体前方脱体激波突然消失,进气道启动,阻塞现象完全消除;随着喉径比不断增加,消除阻塞现象马赫数不断减小,在图4中为3.2Ma,图5和图6为2.8Ma,图7和图8低至2.4Ma,其中,图7在2.4Ma时由于马赫数偏低,入口处两侧斜激波超出激波正常相交条件,形成上下2个λ形激波,相交处的激波类似于正激波,随后激波在喉道腔体内反射交汇,最终在喉道尾端形成膨胀波。图8在2.4Ma时,相比图7在2.4Ma时喉径比增加, 2个斜激波能够正常相交,形成λ形激波。而在2.0Ma时,空心弹已达到消除阻塞现象临界状态,由于马赫数过低,形成的正激波波段较长。综合图2—图8,从压力等值线云图中看出,喉径比和马赫数均是造成阻塞现象的关键因素,当空心弹发生阻塞后,高速来流经激波减速增压形成高压区,极大消耗弹体动能,严重影响存速能力;而阻塞现象消除后,高压区主要集中在腔体内侧,弹体存速能力较强。

图3 θ=20°,HJB=0.3时不同马赫数下压力等值线分布
Fig.3 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.3

图4 θ=20°,HJB=0.4时不同马赫数下压力等值线分布
Fig.4 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.4

图5 θ=20°,HJB=0.5时不同马赫数下压力等值线分布
Fig.5 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.5

图6 θ=20°,HJB=0.6时不同马赫数下压力等值线分布
Fig.6 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.6

图7 θ=20°,HJB=0.7时不同马赫数下压力等值线分布
Fig.7 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.7

图8 θ=20°,HJB=0.8时不同马赫数下压力等值线分布
Fig.8 Pressure contour distribution at different Mach numbers at θ=20°,HJB=0.8
2.2 关键参数对阻力系数影响分析
图9为内锥型空心弹模型分别在锲角取值为20°、30°、40°、50°时,弹丸在不同来流马赫数条件下阻力系数随HJB变化关系图。

图9 不同θ取值时阻力系数随HJB关系变化
Fig.9 the resistance coefficient varies with HJB at different θ values
从图9(a)中可知,在锲角θ=20°,喉径比HJB=0.2时,阻力系数数值在0.35~0.45之间,对常规实心弹而言,阻力系数数值不大,而对于空心弹而言阻力系数数值明显偏大,造成这一现象的直接原因是空心弹进气道气流发生阻塞现象导致进气道未能正常打开,表明喉径比过小,即使马赫数增加,虽能一定程度上降低阻力系数,但没有完全改变进气道气流阻塞现象;在HJB达到0.3时,空心弹仅在3.6Ma工况下阻力系数值骤降至0.05,在0.2~0.3之间出现气流阻塞临界点。随着喉径比不断增加,消除阻塞现象马赫数逐渐减小,最后在HJB达到0.8时,阻力系数均达到最小值0.05。从图3(b)、图3(c)、图3(d)中可以看出,随锲角不断增加,即使HJB不断增大,阻力系数并未呈现出图3(a)中由于进气道阻塞现象消失阻力系数值骤降情况,而是逐渐减小。综合图3,可以得出:在相同锲角和喉径比条件下,增加马赫数能够降低阻力系数;在同一锲角和马赫数条件下,当进气道未打开时,随着HJB增加阻力系数逐渐减小,变化明显,尤其在阻塞临界点附近,阻力系数数值会出现骤降,而在进气道打开阻塞现象消失后,随着HJB增加阻力系数变化并不明显;在HJB和马赫数相同条件下,随着锲角增加,不利于进气道阻塞现象消除,且阻力系数数值会增加。
3 结论
1) 当锲角为20°时,通过改变空心弹喉径比参数,在不同马赫数下仿真,结果表明,在喉径比过小为0.2时,空心弹会发生阻塞现象,增加马赫数不能消除阻塞。消除阻塞前,在同一马赫数条件下,随着喉径比不断增加,阻力系数数值逐渐减小,尤其在阻塞临界点附近,阻力系数数值会出现骤降;消除阻塞后,随着喉径比不断增加,阻力系数数值变化不明显。消除阻塞现象所需马赫数随喉径比增加逐渐减小,喉径比越大越易于消除阻塞问题。
2) 随着锲角的不断增大,当锲角值取30°、40°、50°时,因不能消除阻塞问题,阻力系数数值随喉径比增大逐渐减小,说明锲角的大小对阻力特性影响较大,锲角越大,越易于造成阻塞现象;在喉径比和马赫数相同条件下,锲角越大阻力系数数值越大。
3) 在锲角和喉径比相同时,马赫数越大阻力系数值反而越小。
4) 在空心弹及类似弹丸设计时,需同时兼顾锲角、喉径比和马赫数对气动特性的影响。
[1] 李惠昌,杨金耀,祁荣长.空心弹丸的研究[J].兵工学报,1980,1(2):32-41.LI Huichang,YANG Jinyao,QI Rongchang.Hollow projectile study[J].Acta Armamentarii,1980,1(2):32-41.
[2] 王雨时.西方国家的空心弹技术[J].弹箭技术,1996,9(3):1-10.WANG Yushi.Studying progress on hollow projectile technique in the western countries[J].Projectile &RocketTechnology,1996,9(3):1-10.
[3] 李艳玲,陈志华.口径30 mm空心弹真实条件下的气动特性研究[J].航空计算技术,2011,41(5):76-80.LI Yanling,CHEN Zhihua.Aerodynamic characteristics of hollow projectile with a diameter of 30 mm under real conditions[J].Computing Technique,2011,41(5):76-80.
[4] 陈扬,廖振强,王涛,等.12.7 mm口径空心弹丸空气动力学特性分析[J].系统仿真学报,2010,22 (2):337-339.CHEN Yang,LIAO Zhenqiang,WANG Tao,et al.Aerodynamic characteristics of hollow projectile with a diameter of 12.7mm[J].Journal of System Simulation,2010,22(2):337-339.
[5] 杜宏宝,蒋锋,黄振贵,等.内锥型空心弹阻塞临界入口锥角仿真研究[J].南京理工大学学报,2018,42(6):642-646.DU Hongbao,JIANG Feng,HUANG Zhengui,et al.Simulation of critical inlet angle of inner conical hollow projectile under choke flow[J].Journal of Nanjing University of Science and Technology,2018,42(6):642-646.
[6] 赵强,陈志华.基于近似模型的空心弹气动外形数值优化[J].空气动力学学报,2017,35(3):408-414.ZHAO Qiang,CHEN Zhihua.Numerical optimization of aerodynamic configuration of a hollow projEctile based on the approximation model[J].Acta Aerodynamica Sinica,2017,35(3):408-414.
[7] 张浩,闻泉,王雨时,等.空心弹空气阻力特性计算与数值仿真[J].兵器装备工程学报,2016,37(7):5-11.ZHANG Hao,WEN Quan,WANG Yushi,et al.Theoretical calculations and numerical simulation on air resistance characteristics of hollow projectile[J].Journal of Ordnance Equipment Engineering,2016,37(7):5-11.
[8] 黄振贵,李艳玲,陈志华,等.空心弹的阻力特性与气动外形数值分析[J].兵工学报,2013,34(5):535-540.HUANG Zhengui,LI Yanling,CHEN Zhihua,et al.Numerical investigations on the drag and aero-dynamic characteristics of a hollow projectile[J].Acta Armamentarri,2013,34(5):535-540.
[9] 钱吉胜,李艳玲,陈志华.穿孔对空心弹流场波系结构的影响与分析[J].兵器装备工程学报,2011,32(11):60-62.QIAN Jisheng,LI Yanling,CHEN Zhihua.Impact and analysis on perforation for flow fieldwave system structure of hollowed bullet[J].Journal of Ordnance Equipment Engineering,2011,32(11):60-62.
[10] 全鑫,张红艳,马铁华,等.内锥型空心弹阻塞喉径面积比的仿真研究[J].兵器装备工程学报,2021,42(4):97-101.QUAN Xin,ZHANG Hongyan,MA Tiehua,et al.Simulation research on critical area ratio of throat to entrance of inner conical hollow projectile under choke flow[J].Journal of Ordnance Equipment Engineering,2021,42(4):97-101.
[11] 罗驭川,黄振贵,杜宏宝,等.空心弹结构设计及弹托分离过程仿真[J].兵器装备工程学报,2020,41(5):5-8,31.LUO Yuchuan,HUANG Zhengui,DU Hongbao,et al.Design of hollow projectile structure and simulation of separation process of sabot[J].Journal of Ordnance Engineering,2020,41(5):5-8,31.
[12] EVANS J,WARDLAW A B.Prediction of tubular projectile aerodynamics using the zeus euler code[J].Journal of Spacecraft &Rockets,1989,26(5):314-321.
[13] BRY W A,NUNN R H.Drag of a tubular projectile with internal blockage[J].Journal of Spacecraft &Rockets,1984,21(2):216-217.
[14] NIETUBICZ C J.Navier-Stokes computations for-conventional and hollow projectile shapes at transonicvelocities[C]//14th Fluid and Plasma Dynamics Conference.Palo Alto,CA,USA:AIAA, 1981:23-25.
[15] 李艳玲.低阻空心弹的数值设计研究[D].南京:南京理工大学,2012.LI Yanling.Research on numerical design of low Resistance hollow projectile[D].Nanjing:Nanjing University of Technology,2012.