0 引言
随着红外探测技术的发展,红外探测器在战斗部中的应用也越来越广泛,远程末制导导弹采用红外制导技术后,可以大大提高导弹的抗干扰能力和命中精度[1-6]。同时,作为被攻击目标的水面舰艇及其舰载机,红外干扰弹是其对抗红外制导导弹的主要手段之一,可有效降低目标被击中的概率。导弹攻击和目标防御过程中的关键技术之一就是精确测量目标的红外光谱辐射特性,而使用辐射计对目标进行测量时,辐射计输出的是电压信号[7-9],为了把这些输出信号变成待测的辐射量信号,就必须知道辐射计的响应度[10-15],因此光谱辐射计在采集数据前必须进行标定,否则就不能对采集的数据给出合理的解释,就不能得到辐射强度、辐射亮度的绝对值[16-18]。辐射标定就是建立测量系统入瞳处辐射度量和输出电压信号之间的定量关系,将目标源的辐射特性和光谱仪探测到的特性一一对应起来,从而确定目标的辐射度量的绝对值[19-21]。
光谱分析技术具有快速/准确和绿色检测的特点,在科研、信息、安防等领域有着广泛而且重要的应用,郑麒麟[22]介绍了近年来基于散斑检测的微型计算光谱仪研究进展。高光谱分辨力是未来成像光谱发展的必然趋势,葛明锋等[23]通过不同带宽的定标光源对仪器进行光谱定标提出了通过反积计算法和多像元合并法进行修正,提高了光谱分辨力精度。范纪红[24]针对成像光谱仪建立了一套绝对辐射定标系统,实验验证成像光谱仪绝对辐射定标的不确定度优于5%。
本文中采用的仪器为加拿大LR公司的多功能光谱辐射计,介绍了光谱辐射计的几种定标原理,并验证了其精确度。
1 两点线性定标
1.1 两点线性定标原理
标定时所用的已知辐射源称为校准源,校准源应采用理想的黑体辐射源。为了降低校准的不确定度,本试验采用一级标准黑体作为校准源。将一个一级标准黑体近距离直接对准光谱辐射计进行校准,黑体校准源对辐射计的张角一般应大于辐射计视场的5倍。
理想的辐射计是一个线性系统,即探测器的输出信号与进入探测器的光谱辐射功率成正比,辐射计响应曲线如图1所示。
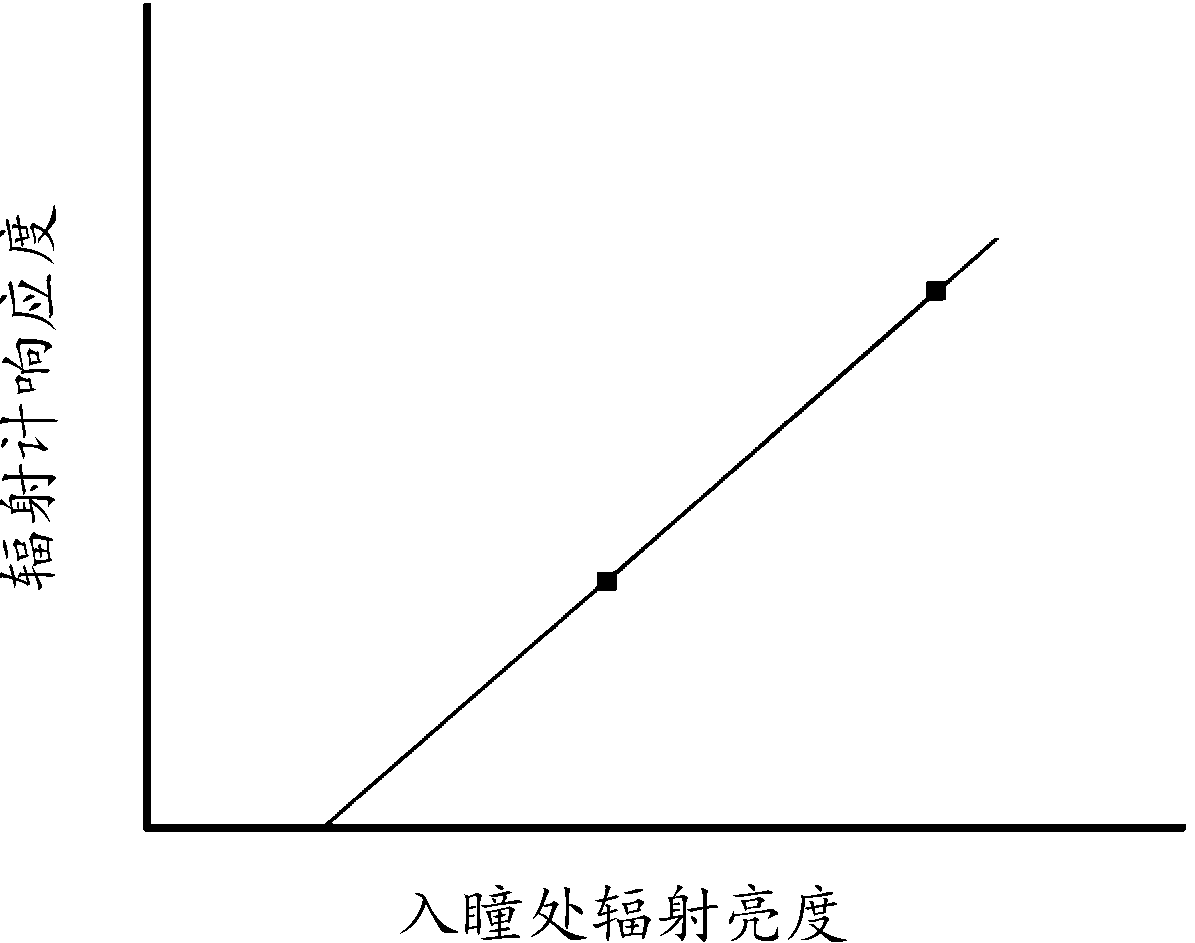
图1 两点线性拟合
Fig.1 Two point linear fitting
因此辐射计的响应度表达式为
R=GL+O
(1)
式(1)中:R为辐射计的光谱响应度;L为辐射计视场的光谱辐射亮度(W/sr/m2/μm);G为辐射计的光谱响应系数;O为辐射计的偏置系数。
采用高/低不同温度的黑体校准源对辐射计进行校准,即可得到两组光谱响应度的数据RC和RH。
Rc=GLC+O
(2)
RH=GLH+O
(3)
其中:LC为低温黑体校准源入瞳处的光谱辐射亮度(W/sr/m2/μm);LH为高温黑体校准源入瞳处的光谱辐射亮度(W/sr/m2/μm);高/低温黑体的辐射亮度LC、LH可以通过lombert余弦定律(4)及Plank辐射定律(5)计算得到。
L=M/π
(4)
![]()
(5)
其中:M为高/低温黑体的光谱辐射出射度(W/m2/μm);T为高/低温黑体辐射源的绝对温度(K);φ为高/低温黑体辐射源的发射率。
根据式(2)和式(3)可以解算出辐射计的光谱响应系数G和偏置系数O。
![]()
(6)
O=RC-GLC
(7)
只要确定了辐射计的光谱响应系数G和偏置系数O,此辐射计就可以测量目标辐射亮量、辐射强度的绝对值。
将测量目标时的系统响应度R代入式(1),即可反算出目标的光谱辐射亮度。
![]()
(8)
式(8)中:L′为反算得到的目标入瞳处的光谱辐射亮度(W/sr/m2/μm);R为测试目标时辐射计的光谱响应度。
1.2 目标测试与误差分析
首先采用50 ℃和300 ℃的高/低温黑体作为校准辐射源对光谱辐射计进行标定,然后用标定后辐射计分别测量80、180、280 ℃黑体的光谱辐射亮度,并将测量值与黑体的理论计算辐射亮度进行对比,试验结果如表1所示。
表1 两点线性标定误差分析
Table 1 Error analysis of two point linear calibration
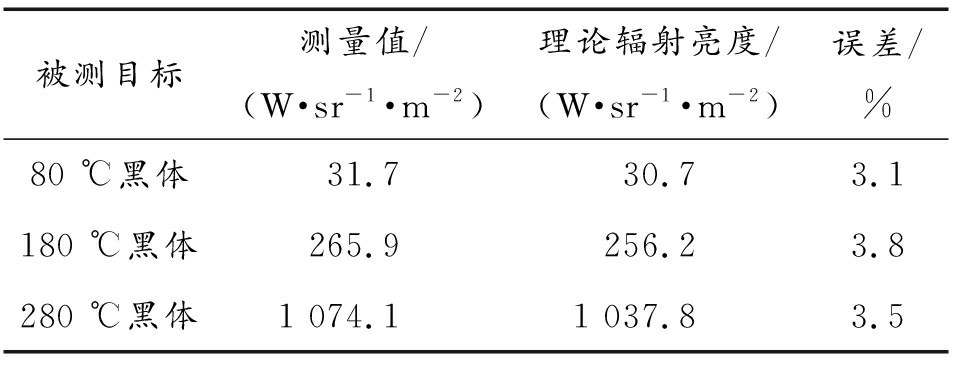
被测目标测量值/(W·sr-1·m-2)理论辐射亮度/(W·sr-1·m-2)误差/%80 ℃黑体31.730.73.1180 ℃黑体265.9256.23.8280 ℃黑体1 074.11 037.83.5
由表1可以看出,被测目标温度变化范围较小时两点线性拟合定标的误差大于3%。
提高高温黑体与低温黑体之间的差值,采用50 ℃和600 ℃ 的高/低温黑体作为校准辐射源对光谱辐射计进行标定,然后用标定后辐射计分别测量150、350、550 ℃黑体的光谱辐射亮度,并将测量值与黑体的理论计算辐射亮度进行对比,试验结果如表2所示。
表2 两点线性标定误差分析
Table 2 Error analysis of two point linear calibration

被测目标测量值/(W·sr-1·m-2)理论辐射亮度/(W·sr-1·m-2)误差/%150 ℃黑体156.8149.54.91350 ℃黑体2 253.22 149.44.83550 ℃黑体9 443.09 027.74.60
由表2可以看出,当被测目标温度变化范围增大时,探测器的非线性响应也越明显,此时采用线性定标测量误差也越大,两点线性拟合定标的误差大于4%。
2 多点线性拟合定标
2.1 多点线性拟合定标原理
为了提高校准谱线的准确性,定标程序可以由2个参考点拓展到多个参考点,多点定标可以减少噪声引起的随机误差和非线性响应引起的系统误差。
多点线性定标可以减少噪声引起的随机误差对校准谱线的影响。对不同温度的黑体校准源进行一系列测量时,就可以产生一系列辐亮度—响应度的校准谱线,多点线性拟合曲线使用所有校准点线性回归得到的,可以更准确地表征测试系统。多点线性拟合示意图见图2所示。

图2 多点线性拟合
Fig.2 Multiple point linear relationship
采用不同温度的黑体校准源对辐射计进行校准,即可得到n组光谱响应度的数据R1、R2、…、Rn。
R1=G(L1+O)
(9)
R2=G(L2+O)
(10)
Rn=G(Ln+O)
(11)
对式(9)—式(11)进行线性拟合后,即可解算出辐射计的光谱响应系数G和偏置系数O。
![]()
(12)
![]()
(13)
确定了辐射计的光谱响应系数G和偏置系数O,将测量目标时的系统响应度R代入式(8),即可反算出目标的光谱辐射亮度。
2.2 目标测试与误差分析
首先采用50、100、150、200、250、300 ℃的黑体作为校准辐射源对光谱辐射计进行标定,然后用标定后的辐射计分别测量80、180、280 ℃黑体的光谱辐射亮度,并将测量值与黑体的理论计算辐射亮度进行对比,试验结果如表3和图3所示。
表3 多点线性拟合定标误差分析
Table 3 Error analysis of multiple points linear calibration

被测目标测量值/(W·sr-1·m-2)理论辐射亮度/(W·sr-1·m-2)误差/%80 ℃黑体31.530.72.7180 ℃黑体262.3256.22.4280 ℃黑体1 064.81 037.82.6

图3 目标黑体的光谱辐射亮度
Fig.3 Spectral radiance of the target blackbody
由表3和图3可以看出,多点线性拟合定标可以降低噪声引起的随机误差带来的影响,误差均低于3%,其准确度明显高于两点定标。
3 非线性多项式拟合定标
3.1 非线性多项式拟合定标原理
多点非线性多项式拟合定标可以减少探测器非线性响应引起的系统误差,多点非线性拟合示意图见图4所示。

图4 多点非线性拟合
Fig.4 Multiple points non linear relationship
非线性拟合中最常用的是用二次函数代替线性函数来模拟系统的非线性响应,辐射计的响应度可以用二次函数表示为
R=Q(L+O)2+G(L+O)
(14)
式(14)中:R为辐射计的光谱响应度;L为辐射计视场的光谱辐射亮度(W/sr/m2/μm);Q为辐射计的非线性响应二次项系数;G为辐射计的非线性响应一次项系数;O为辐射计的偏置系数。
采用3个不同温度的黑体校准源对辐射计进行校准,即可得到3组光谱响应度的数据R1、R2、R3。
R1=Q(L1+O)2+G(L1+O)
(15)
R2=Q(L2+O)2+G(L2+O)
(16)
R3=Q(L3+O)2+G(L3+O)
(17)
根据式(15)—式(17)可以解算出辐射计的光谱非线性响应二次拟合函数的3个参数Q、G和O,然后将测量目标时的系统响应度R代入式(14),即可反算出目标的光谱辐射亮度
![]()
(18)
式(18)中:L′为反算得到的目标入瞳处的光谱辐射亮度(W/sr/m2/μm);R为测试目标时辐射计的光谱响应度。
多点非线性定标程序可以由3个参考点拓展到多个参考点,利用统计回归分析拓展到多项式拟合,多项式拟合的方法与线性拟合的方法基本相同。
3.2 目标测试与误差分析
首先采用100、200、300、400、500、600 ℃的黑体作为校准辐射源对光谱辐射计进行标定,然后用不同标定后辐射计分别测量150、250、350 ℃黑体的光谱辐射亮度,并将测量值与黑体的理论计算辐射亮度进行对比,试验结果如表4和图5所示。
表4 非线性多项式拟合定标误差分析
Table 4 Error analysis of two point linear calibration

被测目标测量值/(W·sr-1·m-2)理论辐射亮度/(W·sr-1·m-2)误差/%150 ℃黑体153.4149.52.58350 ℃黑体2 210.92 149.42.86550 ℃黑体9 246.29 027.72.42
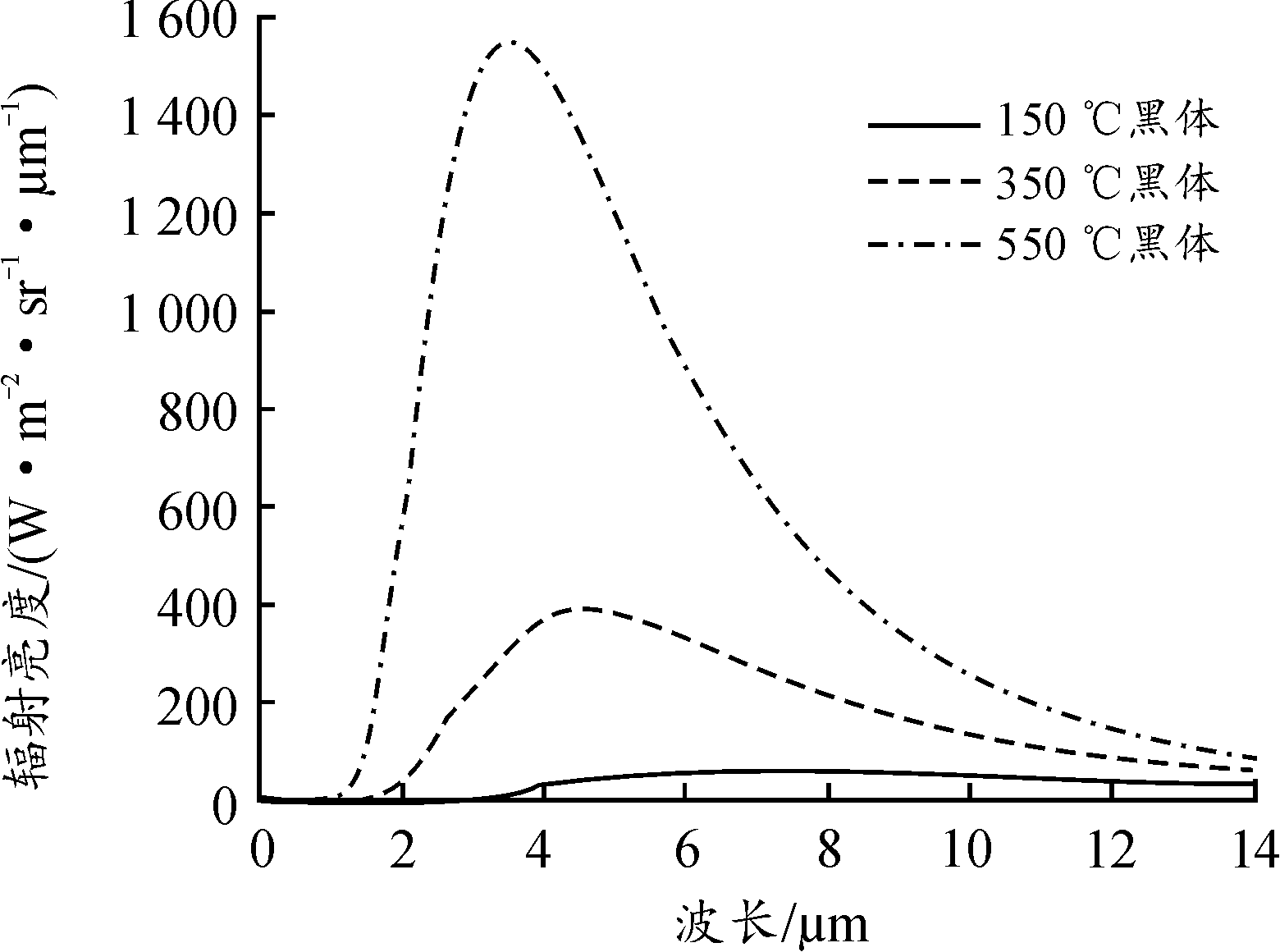
图5 目标黑体的光谱辐射亮度
Fig.5 Spectral radiance of the target blackbody
由表4和图5可以看出,当被测目标温度变化范围增大时,探测器的非线性响应也越明显,此时采用线性定标测量误差也越大。多点非线性定标虽不能消除系统的非线性响应,但是可以明显降低系统非线性响应引起的系统误差,误差均低于3%,其准确度明显高于两点定标。
4 远距离小面源定标
4.1 小面源定标原理
被测目标的温度较高时,就需要较高温度的黑体校准源进行标定,当温度升高时,黑体的辐射量急剧升高,导致辐射计输入信号过大,系统的响应出现饱和现象。为了解决高温定标时辐射计饱和的现象,可采用远距离小面源法标定,即将黑体校准源与辐射计镜头之间隔开一定距离,这种情况下黑体校准源只占辐射计视场的一部分(如图6和图7所示),此时进入辐射计镜头的光谱辐射亮度应为式(19)所示。

图6 黑体在辐射计视场中的示意图
Fig.6 Cut out view of the field of view of a radio meter

图7 极坐标下辐射计视场的视场
Fig.7 Spherical polar coordinates
![]()
(19)
式(19)中:L为辐射计入瞳处的光谱辐射亮度(W/sr/m2/μm);LA为校准辐射源光谱辐射亮度(W/sr/m2/μm);ΩA为黑体所占的立体角(sr);ΩR为辐射计视场的立体角(sr)。
![]()
(20)
式(20)中:EB为背景在入瞳处的光谱辐射照度(W/m2/μm);LB为背景的光谱辐射亮度(W/sr/m2/μm)。
假设背景的辐射亮度不随角度变化,那么式(19)可以修改为
![]()
(21)
式(21)中:ΩB为背景所占的立体角(°)。
ΩB、ΩR和ΩA的关系为式(22)所示。
ΩB=ΩR-ΩA
(22)
黑体校准源所占的立体角由式(23)计算:
![]()
(23)
式(23)中:A为黑体校准源的辐射面积(m2);R为黑体校准源与辐射计之间的距离(m)。
采用高/低不同温度的黑体校准源对辐射计进行校准,即可得到2组光谱响应度的数据RC和RH。
![]()
(24)
![]()
(25)
其中:LAC为低温黑体入瞳处的辐射亮度(W/sr/m2/μm);LAH为高温黑体入瞳处的辐射亮度(W/sr/m2/μm)。
根据式(24)和式(25)可以解算出辐射计的光谱响应系数G和偏置系数O。
![]()
(26)
![]()
(27)
同样只要确定了辐射计的光谱响应系数G和偏置系数O,此辐射计就可以测量目标辐射亮量、辐射强度的绝对值。
将测量目标时的系统响应度R代入式(8),即可反算出目标的光谱辐射亮度。
4.2 目标测试与误差分析
首先采用500 ℃和800 ℃的高/低温黑体作为校准辐射源对光谱辐射计进行标定,然后用标定后辐射计分别测量600 ℃和700 ℃黑体的光谱辐射亮度,并将测量值与黑体的理论计算辐射亮度进行对比,试验结果如表5和图8所示。
表5 高温黑体目标的辐射亮度与理论计算值误差分析
Table 5 Comparison between measured and theoretical radiance of high temperature blackbody

测试对象8~14 μm/%3~5 μm/%1~3 μm/%600 ℃黑体1.71.21.8700 ℃黑体1.81.11.9
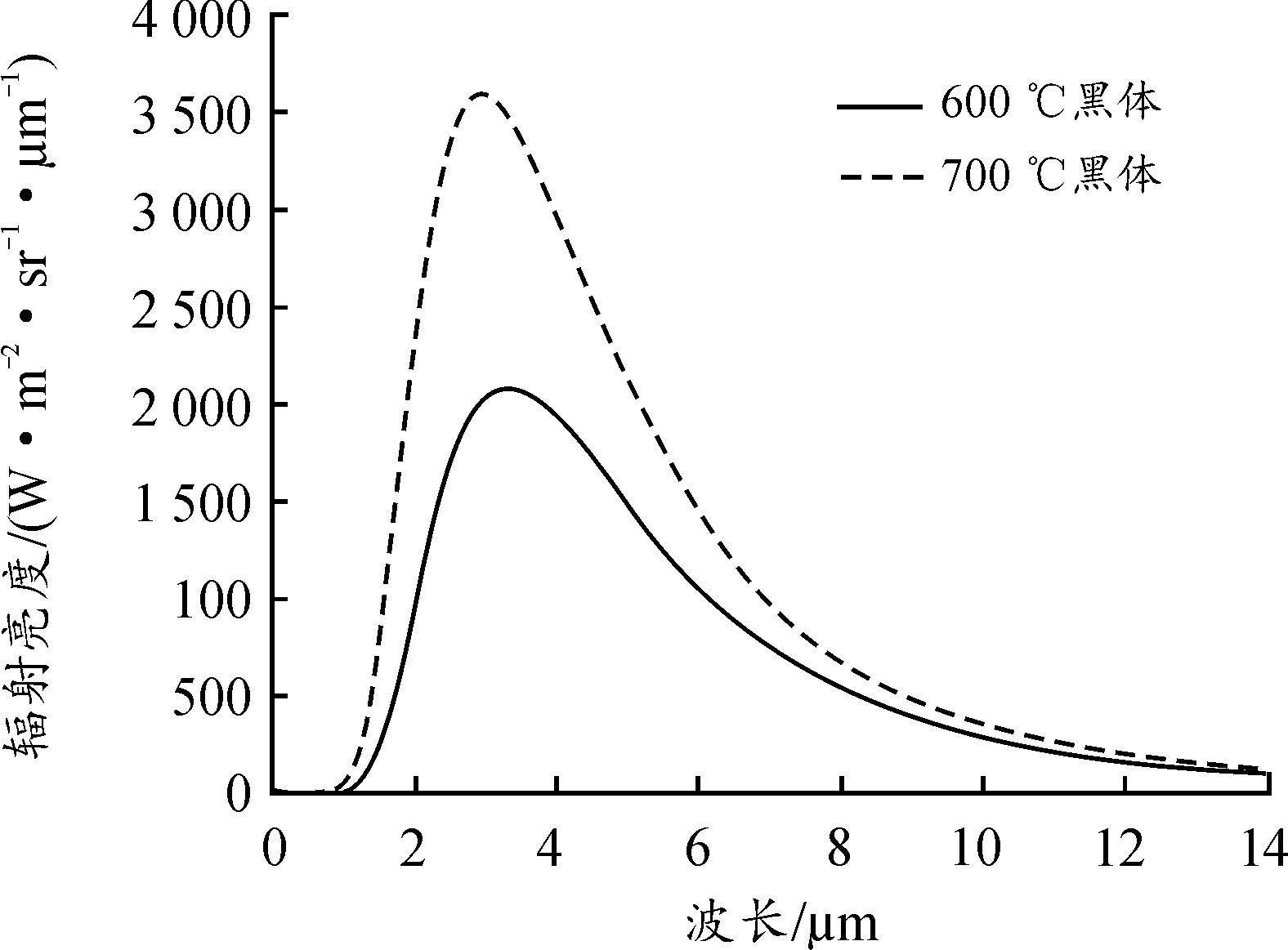
图8 目标黑体的光谱辐射亮度
Fig.8 Spectral radiance of the target blackbody
通过表5和图8可以看出,当被测目标温度较高时,光谱辐射计入瞳处辐射亮度较大,为防止测试系统的响应出现饱和现象,宜采用远距离小面源法标定,此标定方法的测试误差低于2%。
5 结论
通过多种定标方式对比可以得出如下结论:
1) 被测目标温度变化范围越大,采用两点线性标定误差越大;
2) 多点定标可减小噪声引起的随机误差和非线性响应引起的系统误差,当被测目标温度较低时,应根据被测目标温度变化范围选择多点线性拟合定标或多点非线性拟合定标;
3) 被测目标温度变化范围较小时,宜采用多点线性拟合定标,以减少噪声引起的随机误差带来的影响;
4) 被测目标温度变化范围较大时,宜采用多点非线性拟合定标,以减少非线性响应引起的系统误差带来的影响;
5) 当被测目标温度较高时,光谱辐射计入瞳处信号较大,宜采用远距离小面源法标定,测量误差低于2%。
[1] 贾曜峰,王玉鹏,沈宏海.太阳辐射计直射通道定标方法研究[J].激光与红外,2023,53(5):63-67.JIA Yaofeng,WANG Yupeng,SHEN Honghai.Research on the calibration method of direct radiation channel for solar radiometers[J].Journal of Laser and Infrared,2023,53(5):63-67.
[2] 王怡,王浩,卫子毓.基于光谱辐射计的航空发动机红外辐射特性测试方法[J].红外技术,2023,45(3):21-25.WANG Yi,WANG Hao,WEI Ziyu.Test method for infrared radiation characteristics of aircraft engines based on spectral radiometer[J].Journal of Infrared technology.2023,45(3):21-25.
[3] 张允祥,李新,黄冬红.外通道式野外辐射计的光机设计及性能测试[J].红外与激光工程,2022,51(12):31-34.ZHANG Yunxiang,LI Xin,HUANG Donghong.Optical and mechanical design and performance testing of external channel field radiometer[J].Journal of Infrared and Laser Engineering,2022,51(12):31-34.
[4] 袁林光,范纪红,周晓光.近紫外到近红外光谱辐射计及定标方法研究[J].应用光学,2019,40(3):16-20.YUAN Linguang,FAN Jihong,ZHOU Xiaoguang.Research on the calibration method of near-ultraviolet to near-infrared spectroradiometers[J].Journal of Applied Optics,2019,40(3):16-20.
[5] 贾瑞栋,夏志伟,王玉鹏.太阳光谱辐照度绝对测量及其定标单色仪[J].发光学报,2017,38(8):15-20.JIA Ruidong,XIA Zhiwei,WANG Yupeng.Absolute measurement of solar spectral irradiance and its calibration monochromator[J].Chinese Journal of Luminescence,2017,38(8):15-20.
[6] 衣小龙,方伟,李叶飞.太阳辐照度绝对辐射计的定标新方法[J].红外与激光工程,2016,45(9):13-16.YI Xiaolong,FANG Wei,LI Yefei.A new calibration method for solar irradiance absolute radiometer[J].Journal of Infrared and Laser Engineering,2016,45(9):13-16.
[7] GRAY G J, AOUF N, RICHARDSON M A,et al.An intelligent tracking algorithm for an imaging infrared anti-ship missile [J].Proc.of SPIE,2012,8543.
[8] GRAY G J, AOUF N, RICHARDSON M A,et al.Feature-based recognition approaches for infrared anti-ship missile seekers[J].The Imaging Journal,2012,60.
[9] DIAO Xiaofei,TAN Jiubin,HU Pengcheng,et al.Frequency stabilization of an internal mirror He-Nelaser with a high frequency reproducibility [J].Applied optics,2013,52(3):456-460.
[10] LIU Jian,JI Honghu.Experimental investigationon infrared signaturesof axisymmetric vectoring exhaust nozzle with film cooling and low-emissivity coating[J].Journal of Engineering for Gas Turbines and Power,2018,140(9):091203.
[11] QIAN J,LIU Z,SHI C,et al.Frequency stabilization of internal-mirror He-Ne lasers by air cooling[J].Applied Optics,2012,51(25):6084-6088.
[12] EOM T B,CHOI H S,LEE S K.Frequency stabilization of an internal mirror He-Ne laser by digital control[J].Review of scientific instruments,2002,73(1):221-224.
[13] L.Dejiao,D.Gaoliang,Y.Chunyong,et al.Frequencystabilization of transverse Zeeman He-Ne laser bymeans of model predictive control[J].Rev.Sci.Instrum.,2006,77,123301.
[14] NIEBAUER T M, FALLER J E, GODWIN H M,et al.Frequency stability measurements on polarization stabilized He-Ne lasers[J].Appl.Opt.,1988,27:1285-1289.
[15] ROWLEY W R C.The performance of a longitudinal Zeeman stabilized He-Ne laser (633 nm) with thermal modulation andcontrol[J].Meas.Sci.Technol.1990,1:348-351.
[16] ZEMANEK P, LAZAR J.Use of the beat frequency betweentwo modes for frequency stabilization of internal-mirrorlasers[J].Appl.Opt.,1994,33:6333-6339.
[17] CIDDOR P E, DUFFY R M.Two-mode frequency-stabilised He-Ne (633 nm) lasers:studies of short- and long-term stability[J].J.Phys.E,1983,16:1223-1227.
[18] UMEDA N, TSUKIJI M, TAKASAKI H.Stabilized 3He-20Ne transverse Zeeman laser[J].Appl.Opt.,1980,19:442-450.
[19] ZUMBERGE M A.Frequency stability of a Zeeman-stabilizedlaser[J].Appl.Opt.,1985,24:1902-1904.
[20] SASAGAWA G S, ZUMBERGE M A.Five-year frequency stabilityof a Zeeman stabilized laser[J].Appl.Opt.,1989,28:824-825.
[10] BAER T, KOWALSKI F V, HALL J L.Frequency stabilizationof a 0.633 micron He-Ne longitudinal Zeeman laser[J].Appl.Opt.,1980,19:3173-3177.
[21] HU P C, TAN J B,YAN L,et al.Preheating methodfor frequency stabilized Zeman He-Ne laser based on temperaturetrajectory control[J].Opt.Precis.Eng.,2008,16:1009-1017.
[22] 郑麒麟,文龙,陈沁.基于散斑检测的微型计算光谱仪研究进展[J].光电工程,2021,48(3):200183.ZHENG Qilin,WEN Long,CHEN Qin.Research progress of computational microspectrometer based on speckle inspection[J].Journal of Applied Optics,2021,48(3):200183.
[23] 葛明锋,亓洪兴,王雨曦,等.高分辨力成像光谱仪光谱定标研究[J].光电工程,2015,42(12):14-19.GE Mingfeng,QI Hongxing,WANG Yuxi.Spectral calibration for the high spectral resolution imager [J].Journal of Applied Optics,2015,42(12):14-19.
[24] 范纪红,赵生禄,占春连.成像光谱仪绝对辐射定标技术研究[J].应用光学,2013,34(4):629-632.FAN Jihong,ZHAO Shenglu,ZHAN Chunlian.Research on absolute radiation calibration technology of imaging spectrometer[J].Journal of Applied Optics,2013,34(4):629-632.