0 引言
爆炸物在引爆之后,变成高温、高压气体,该气体被周围的水包围形成气泡。气泡内部的高压将驱使周围的流体以小于声速的速度向外扩散运动,在此阶段,将水看成不可压缩的介质。由于惯性作用,气泡将过度膨胀,同时其内部压力减小,直至仅占外部流体静水压很小一部分,气泡表面的负压差使气泡的膨胀运动停止,并使气泡产生收缩运动,收缩过程由流场中周围流体静压力驱动,该过程将会继续直至不断增加的内部气泡压力将该过程瞬间逆转过来。气体和水的弹性特性为气泡振荡提供条件,该过程被称为气泡脉动,脉动过程直至气泡破裂为止。气泡排开一部分密度比内部气体大的流体,排开的流体质量远远超过了气泡内部气体的质量,这就提供了浮力。浮力使气泡向上移动,由浮力及重力作用产生的气泡运动及其向上迁移过程如图1所示。爆炸气泡在外力的作用下,发生径向的膨胀-收缩运动,同时还会发生垂直向上的运动。当气泡体积第1次收缩到最小时垂向运动的位移,也就是气泡首次收缩到最小时的上浮量(后简称气泡上浮量),是水下爆炸计算中相当重要的一个量,因为这一因素决定着气泡脉动压力源的位置。关于气泡上浮量的计算,国内外学者开展了大量的研究[1-8]。Cole假设上浮量和周期以泰勒的无因次单位表示,则气泡上升量Δh′正比于振动周期(精度在10%以内),得到理想状态下,气泡上浮量的计算公式
揭示了理想自由状态下,上浮量Δh与药量W成正比,与相对布深Z0成反比。英国学者EH.Kennard在《水下爆炸研究》第2卷给出另一种计算公式Δh= 22W1/2/Z0。2种计算公式在一定范围内比较吻合。中国船舶科学研究中心对已有数据进行分析拟合,得到了简单、实用、精度良好的计算公式,上浮量Δh=2.2W1/3e(-H/(3.85W(1/3)+31.15))公式需满足水深H大于20 m,当量小于1 000 kg当量条件。从计算公式来看,影响上浮量的主要因素为装药量与静压,而静压的影响因素为爆源布深。国内学者采用高速摄影技术对气泡运动过程进行了研究[9-15],其试验方法、试验数据、数据处理过程、气泡运动特征规律等,为开展上浮量研究奠定基础。
图1 自由场爆炸气泡脉动及载荷特性
Fig.1 Characteristics of bubble pulsation and load in free situation
文中首先基于气泡测量周期对水下爆炸气泡上浮量进行计算,并与理论计算结果进行比较;其次基于上浮量与冲击波峰压值对应距离,计算气泡脉动峰压值,并与测量值进行比对;再次考虑边界条件的影响,对上浮量进行计算,并与测量上浮量进行比对分析。
1 气泡上浮量计算模型
气泡上浮量的计算包括2种,一是根据上浮量与脉动周期之间的对应关系,由测量周期计算上浮量。二是根据冲击波峰压对应的距离、气泡峰压对应的距离、上浮量三者之间的相对位置关系,计算气泡上浮量。
1.1 上浮量、周期之间的对应关系
假设重力是作用于水上唯一的力,而水的惯性所产生的阻力是流体运动唯一的阻力。若现象的线性比尺是变化的,则保持2种运动相似的时间比尺的相应变化,应当是重力(流体静压力)的影响在任何系统内部相同。若此条件得到遵守,则因次为长度/时间2的重力加速度g这一常量要求:时间比尺增加为长度比例系数的平方根。关系式用特征长度L来表示[1]:
(1)
(2)
式(1)、式(2)中:Y为冲击波过后气泡内残留的能量(J); ρ0为周围水介质的密度(kg/m3)。
对于TNT装药而言,
药量(kg)。
气泡到达第一次最小体积时的位移是相当重要的因素,因为这一因素决定这气泡脉动源的位置。以泰勒的无因次单位表示,气泡上浮量Δh′=1.05T′正比于振动周期(精度在10%以内),这个关系式可以写成:
Δh′=1.05T′
(3)
代入长度、时间无量纲化表达式,则有:
(4)
Δh=
6.34×W1/8×T
(5)
式(5)中:Δh为气泡上浮量(m);T为气泡脉动周期(s)。
根据长度、时间的无量纲化表征可得到式(5),由式(5)可知,自由场的情况下,气泡上浮量与脉动周期、装药量有关,通过脉动周期测量值可计算得到上浮量。
1.2 无限水域气泡上浮量计算
理想状态下,气泡上浮量的计算公式[1]为
(6)
式(6)中,Z0为相对布放深度(m)。
1.3 考虑边界条件影响的上浮量计算
边界主要考虑自由表面和刚性底对气泡上浮的影响。刚性表面和自由表面的存在影响气泡脉动时的中心位移。定性地看来,边界的影响与流场惯性的变化有关。刚性表面的存在破坏了气泡附近水的径向流动。开始时,气泡内部压力大于静水压力,气泡表面朝障碍物方向的水较难发生位移,气泡遂离开障碍物。但是,气泡内部压力大于静水压力的时间占整个脉动周期的比例较小,且这个时间段内气泡较小,所以这种效应相当微小。当气泡内部压力小于静水压力时,朝向气泡表面的流的加速度,在靠近障碍物的一侧不容易发生,因此,流使气泡向障碍物靠近。这种现象比气泡内部压力大于静水压力时的排斥明显得多,以致气泡的主要运动是受到吸引。
自由表面对气泡的位移起相反的影响,因为这时表面附近的水可以自由移动,但是流体压力等于大气压。当气泡开始膨胀时,气泡上面的水惯性更小,比气泡下面的水更快地被替代,则气泡向上运动。当气泡内部压力小于静水压力时,由于自由表面的水特别容易得到朝向气泡的加速度,所以产生向下的水流,气泡从自由表面向下运动。
考虑边界的影响,其测量上浮量(或者修正上浮量)计算公式如下:
(7)
式(7)中:Δh为无限水域气泡上浮量(m);Δh*为自由水面和刚性水底联合作用下的气泡上浮量(m); η为修正系数;am为无限水域气泡最大半径(m);d为药包距自由表面距离(m);b为药包距水底距离(m)。
对试验测量结果进行拟合,得到TNT修正系数,η取2.77。表1、表2为部分实验数据。
表1 基于测量周期的水下爆炸气泡上浮量计算
Table 1 Calculation of bubble up-float distance based on measurement period
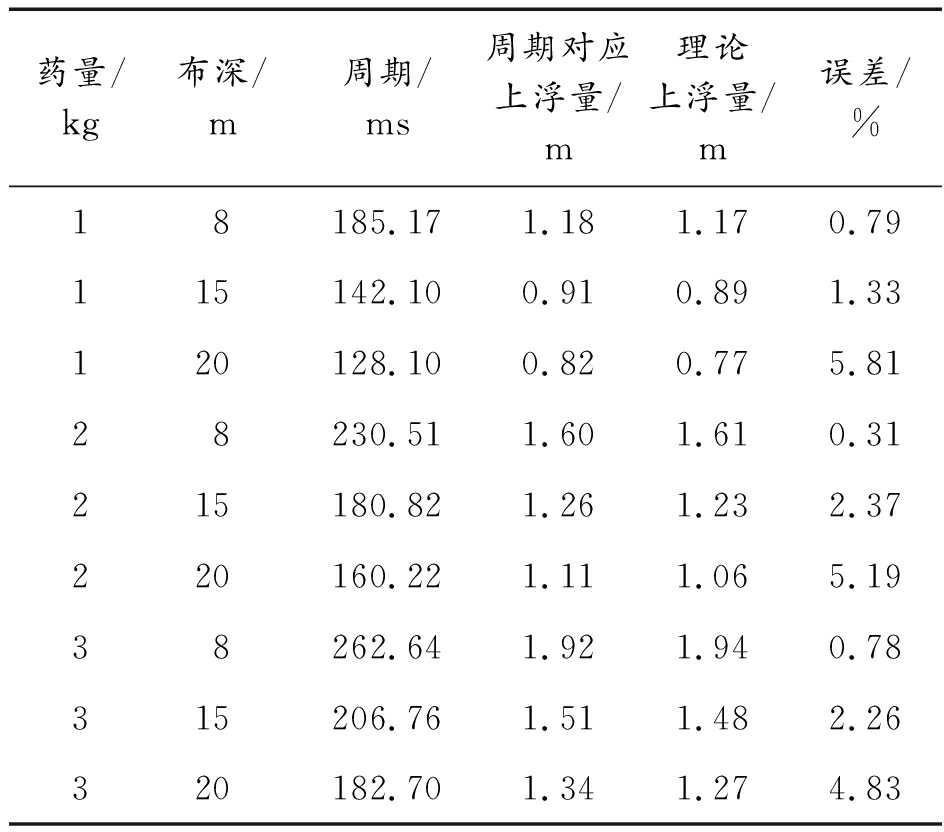
药量/kg布深/m周期/ms周期对应上浮量/m理论上浮量/m误差/%18185.171.181.170.79115142.100.910.891.33120128.100.820.775.8128230.511.601.610.31215180.821.261.232.37220160.221.111.065.1938262.641.921.940.78315206.761.511.482.26320182.701.341.274.83
表2 气泡脉动峰压值比较
Table 2 Comparison of bubble pulsation pressure maximum
药量/kg布深/m冲击波峰压/MPa冲击波峰压对应距离/m测量气泡峰压/MPa周期/ms计算上浮量/m气泡距离/m计算气泡峰压/MPa气泡峰值比值18125.60.465.70185.171.181.273.470.61115131.40.447.27142.100.911.013.990.55120125.60.467.34128.100.820.944.170.5728125.70.584.72230.511.601.713.330.71215124.70.586.04180.821.261.393.780.63220126.80.585.81160.221.111.254.020.6938126.20.664.21262.641.922.033.250.77315126.70.666.92206.761.511.653.690.53320127.40.665.44182.701.341.493.930.72
2 基于测量周期的上浮量计算分析
在水深28 m的开阔露天水池中,药包布深分别位于水下8、15、20 m,采用1、2、3 kg TNT炸药,进行爆炸试验,对冲击波及气泡压力进行测量,测点距药包水平距离分别为0.5、0.63、0.72 m,得到气泡脉动周期参数。结合试验数据,基于测量周期,采用式(5)对上浮量进行计算,结果如表1所示。
由表1可知,通过气泡脉动周期计算得到的气泡上浮量与理论上浮量误差不大,两者比较吻合。随着布放深度的增加,误差值偏大。产生此种情况的主要原因是边界条件的影响。一方面边界条件对周期的影响特点为:自由面的影响使气泡脉动周期减小,底部的作用使气泡脉动周期增加,存在一个最佳布深,使得两者的作用相互抵消;另一方面,边界条件对上浮量的影响为:自由面对上浮量起到排斥作用,底部对上浮量起到吸引作用,两者都会使上浮量变小。在靠近自由面的区域,底部的作用可以忽略,主要为自由面对气泡的作用,一方面使周期变小,另一方面使上浮量变小,两者变化趋势一致,因此计算误差偏小。在靠近底部的区域,自由面的影响可以忽略,主要为底部对气泡的作用,一方面底部的存在使气泡周期变大,另一方面底部吸引作用使上浮量变小,两者变化趋势不一致,因此导致偏差变大,计算误差变大。
3 基于上浮量计算气泡脉动峰压比值
当测点与爆源位于同一水平位置时,在一个脉动周期内,气泡垂直上浮量Δh、冲击波对应距离Rs、气泡脉动对应距离Rb构成直角三角形关系,如图2所示。
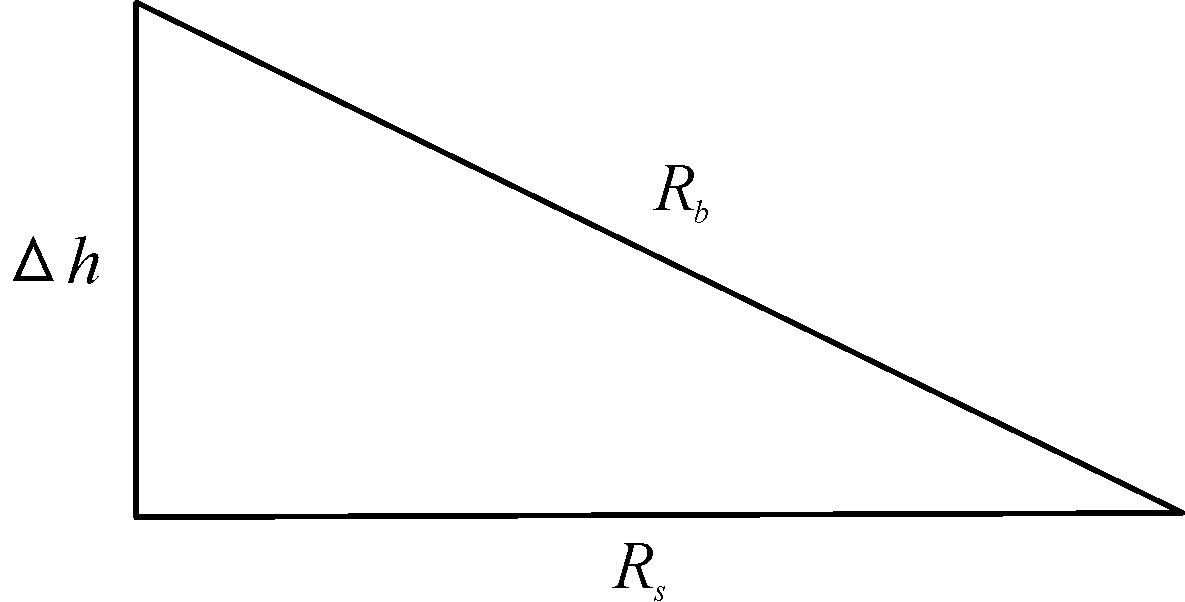
图2 上浮量计算示意图
Fig.2 The diagram of up-float calculation
根据气泡上浮量、冲击波峰值对应距离可计算出气泡峰压对应的距离,如式(8)所示:
(8)
式(8)中:Rb气泡峰压对应的距离(m);Rs冲击波峰值对应距离(m)。
由Rb及相关参数可计算气泡脉动峰压值Pbmc,如式(9)所示:
Pbmc=Kb(W1/3/Rb)β
(9)
式(9)中:Pbmc为气泡脉动峰压值(MPa);对于TNT而言,Kb取4.01, β取0.61。
计算得到的气泡脉动峰压值可与测量得到的峰压值进行比对,结果如表2所示。
由表2可知,两者比值介于0.53～0.77之间。在计算过程中,气泡脉动压力峰值的测量值由于包含了空化因素的影响,测量值偏大,在计算距离时,需要乘以系数进行修正。Pbmax=μPbmc,Pbmc为气泡峰压测量值,TNT系数μ一般取0.53～0.77,平均值为0.62。气泡脉动峰值压力测量值拟合如图3所示。
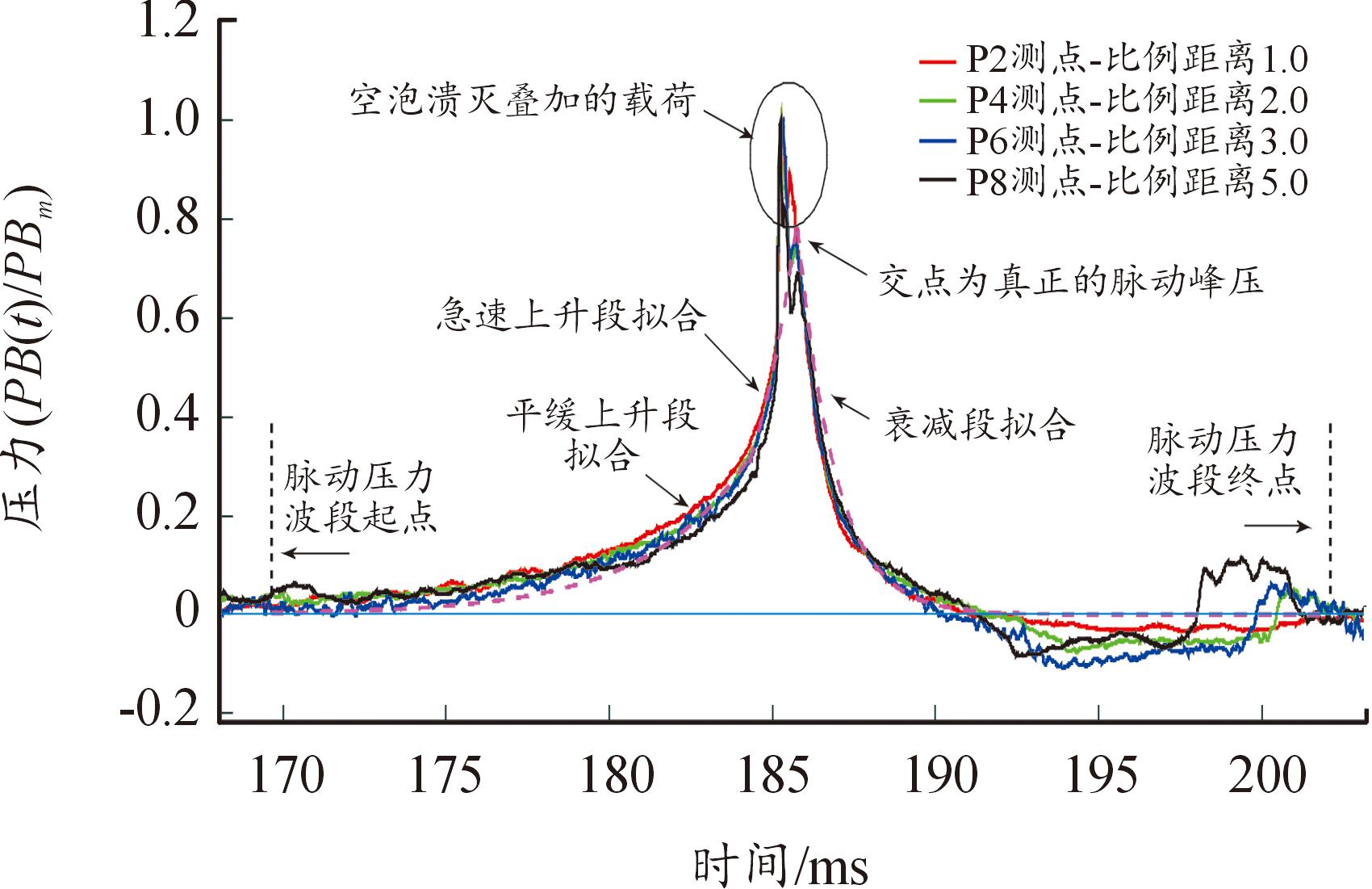
图3 1 kg TNT水深8 m时气泡脉动压力波拟合结果
Fig.3 The fitting results of bubble pulsation pressure(1 kgTNT 8 m depth)
试验测量的气泡脉动压力波实际上受水面及水底影响,已经与理想自由场情形存在一定差异,尤其是波头部分“畸变”更加明显。根据现有的气泡脉动压力波时程模型对试验进行了拟合,得到了更接近自由场的各装药气泡脉动压力波时程修正模型。拟合过程中认为其压力波上升段及衰减段是“正常”的,因此在拟合时的原则就是不追求波头的一致性,而是上升段及衰减段的吻合性。将气泡脉动压力波分为缓慢上升段、急速上升段及衰减段3个部分,如图3所示。并且气泡脉动峰压测量结果一般偏大。
气泡脉动压力波头是存在一定畸变的,并不是“理想”的符合理论模型的双指数波头,引起畸变的原因可能是水表面空化溃灭载荷叠加,也可能是受水面或水底等边界影响,气泡收缩膨胀转换时压力波的释放有所改变。
4 冲击波峰压、气泡峰压计算上浮量
4.1 上浮量计算方法
由于气泡脉动源一直在向上运动,压力辐射源是一移动源,当爆炸点距自由面比较近,到气泡第1次压缩到最小时已经上浮相当的距离,必须以气泡压缩至最小的位置作为脉动压力的源点。当测点与爆源位于同一水平位置时,在一个脉动周期内,气泡垂直上浮量、冲击波对应的距离、气泡脉动对应的距离构成直角三角形关系。
电测试验获取冲击波压力峰值以及气泡压力峰值,假定爆炸初始时刻传感器测点与爆源在同一布深,2个对应距离和上浮量构成直角三角形关系,因此开展上浮量计算。
冲击波峰压Psmax为
Psmax=Ks(W1/3/Rs)α
(10)
冲击波峰压对应距离Rs为
Rs=W1/3(Psmax/Ks)-1/α
(11)
式(11)中: Psmax为冲击波峰压(MPa);Rs为冲击波峰压对应距离(m);Ks =52.7;α=1.13。
冲击波峰值对应距离Rs值和测点距离近似相等,也可用测点距离R直接替代。
气泡峰压为
Pbmax=Kb(W1/3/Rb)β
(12)
气泡峰压对应距离为
Rb=W1/3(Pbmax/Kb)-1/β
(13)
式(13)中: Pbmax为气泡峰压(MPa);Rb为气泡峰压对应距离,(m);Kb =4.01; β=0.61。
上浮量为
(14)
理论上来讲,气泡的上浮速度为数十米每秒,声波在式中的传播速度为1 500 m/s左右,相对而言上浮速度为小量,冲击波与气泡脉动时间差导致的距离误差可以忽略。在一般情况下,上浮量相对于爆距而言是小量,因此爆距大小对上浮量计算精度影响很大,在保证传感器安全的情况下,爆距越小,计算精度越高。
如果测点位于爆源的正上方或者最下方,则上浮量数值为冲击波峰值与气泡峰值对应距离的差值。
Δh=|Rb-Rs|
(15)
4.2 计算结果比较
对气泡脉动峰值进行修正,采用式(14)对上浮量进行计算,结果如表3所示。
表3 水下爆炸气泡上浮量计算结果
Table 3 Calculation results of bubble up-float distance
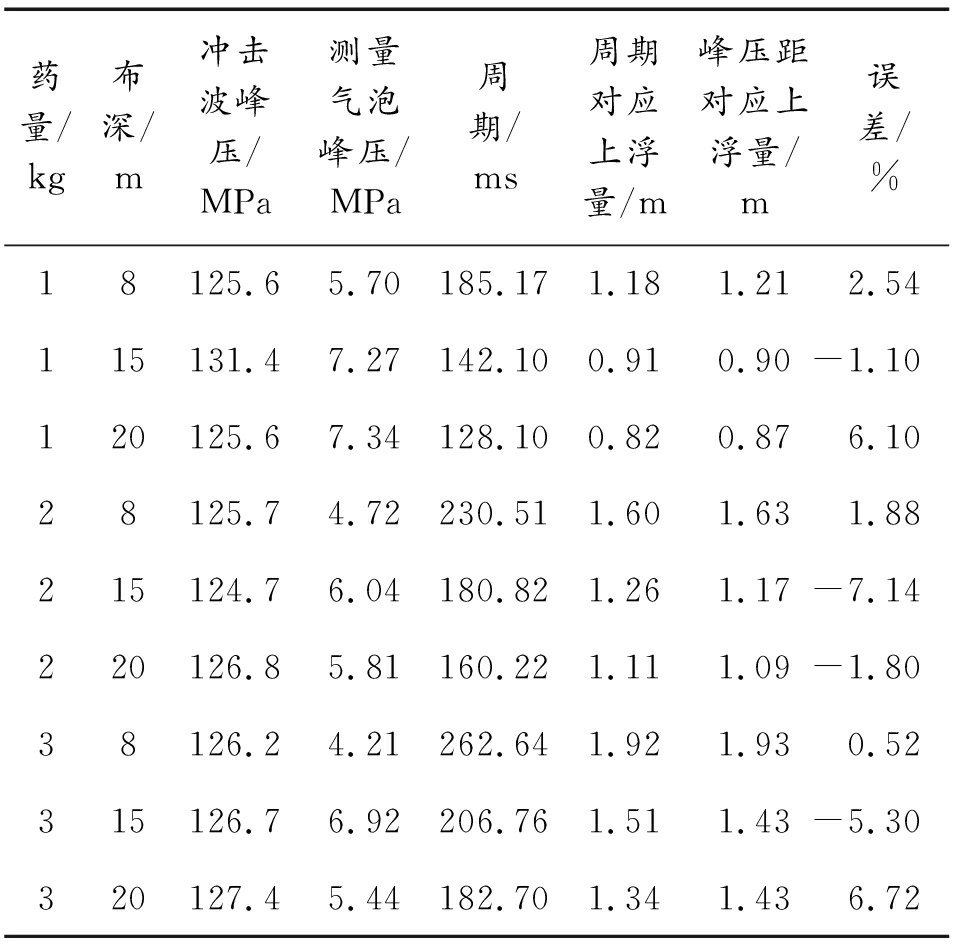
药量/kg布深/m冲击波峰压/MPa测量气泡峰压/MPa周期/ms周期对应上浮量/m峰压距对应上浮量/m误差/%18125.65.70185.171.181.212.54115131.47.27142.100.910.90-1.10120125.67.34128.100.820.876.1028125.74.72230.511.601.631.88215124.76.04180.821.261.17-7.14220126.85.81160.221.111.09-1.8038126.24.21262.641.921.930.52315126.76.92206.761.511.43-5.30320127.45.44182.701.341.436.72
由表3可知,通过气泡脉动峰压值修正得到的上浮量与基于气泡脉动周期计算得到的气泡上浮量相比,两者差别不大,平均误差为3.68%,满足工程实践要求。由于公斤级爆源产生的气泡尺寸较大,难以用高速摄影拍摄,所以上浮量计算以压力测量数据进行分析。
4.3 峰值计算距离特点
通过研究,发现冲击波峰值、气泡脉动峰值计算距离时存在一定的差异,总结特点如下:
1) 冲击波峰值计算距离
通过冲击波峰值计算得到的距离与初始爆距值比较接近,初始阶段流场受影响比较小,同时由于冲击波峰值脉宽窄、峰值突变明显等特点,测量值与计算值比较接近。
2) 气泡脉动峰值计算爆距
气泡脉动峰值发生在冲击波作用后一个脉动周期时刻,流场发生一定的变化,产生一定的空化效应,测量的结果通常大于气泡脉动的实际结果,需要对其进行修正。同时气泡脉动峰值脉宽相对较宽、很多情况下变化还不规则,需要进行拟合处理。用气泡脉动峰值直接测量结果进行上浮量计算得到的结果偏差比较大,用气泡脉动峰值修正结果进行计算,得到的结果与理论值比较接近。因此在计算时,需要对测量结果进行修正,对于TNT而言,修正系数一般可选择0.6～0.7。
5 试验结果分析比对
药量越小,气泡尺寸越小,受边界影响越小;同时药量小,气泡尺寸小,可借助高速摄影对气泡运动情况进行拍摄。借助小药量试验数据,将压力传感器测量得到的上浮量同高速摄像拍摄得到的上浮量进行比较,验证计算方法的正确性。
5.1 小当量炸药测量结果
试验在爆炸水池中进行,水深5 m,20 g爆源布深为3.0～3.2 m,采用高速相机获取气泡运动过程,全程摄像且图像采集速率1 000帧/s。采用图像处理软件对装药水中爆炸高速摄像结果进行了处理,得到了气泡脉动周期、最大气泡半径、气泡中心上浮轨迹、气泡半径变化曲线等参数,典型工况测量结果如图4所示。红色曲线为上浮量随时间变化曲线,蓝色曲线为气泡半径随时间变化曲线。由图4可知,在此工况下,最大气泡半径为395.0 mm,气泡二次脉动时刻为69.0 ms,对应最小气泡半径为65.3 mm;气泡上浮量在气泡溃灭最小半径附近开始增加。
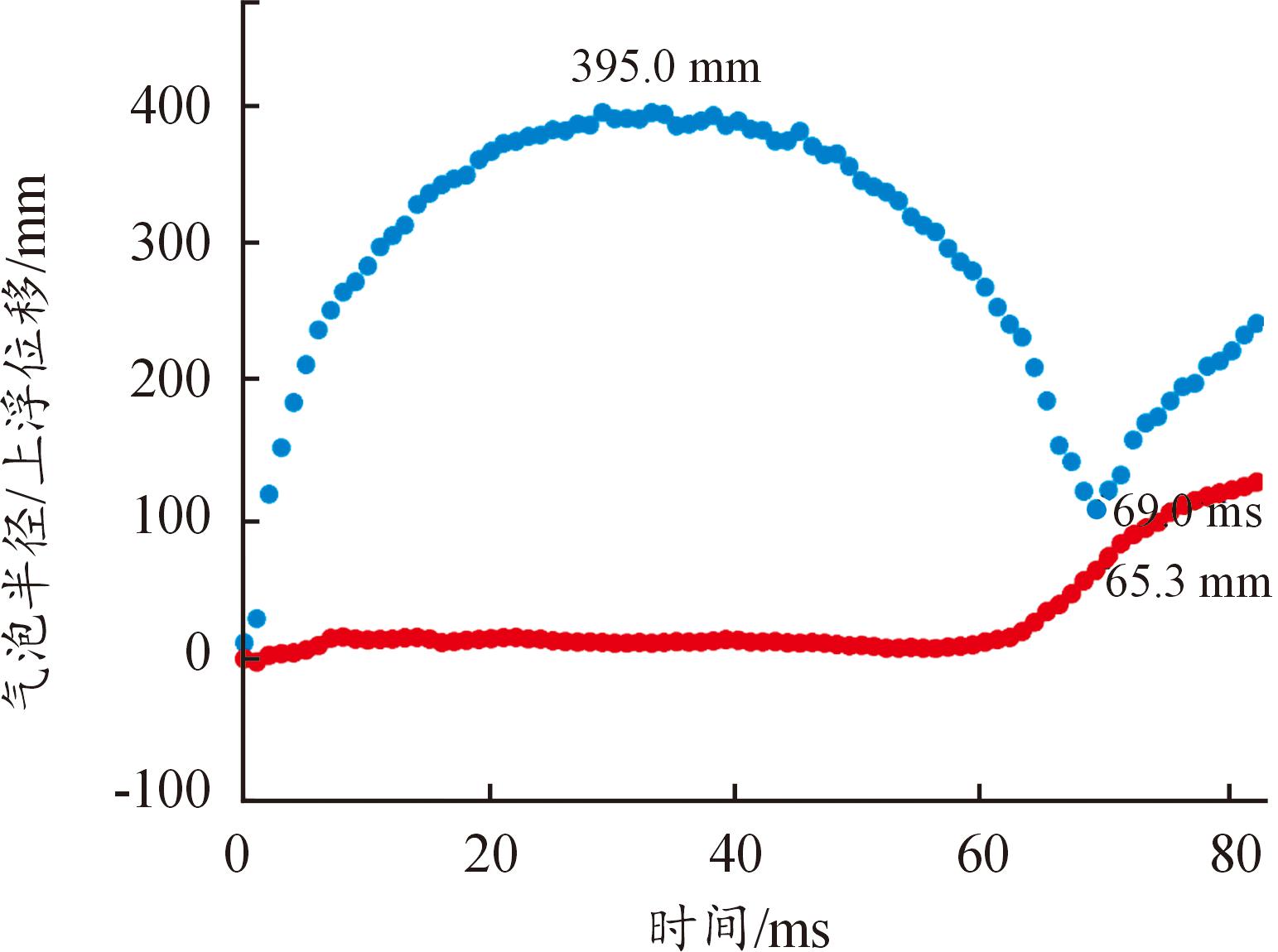
图4 气泡半径和上浮量时程曲线
Fig.4 Curves of bubble radius and up-float
5.2 考虑边界影响的上浮量比对
试验测量结果,参考药量20 g,爆源布深分别位于水下3.2 m、3.0 m的试验工况;气泡峰压对应距离的计算过程中,峰值修正系数取0.62,计算结果如表4所示。
表4 考虑边界条件的上浮量计算
Table 4 Calculation of bubble up-float distance considering boundary condition
药量/g定深/m测点距离/m冲击波峰压/MPa冲击波距离/m气泡峰压/MPa气泡距离/m上浮量(计算)/m上浮量(测量)/m上浮量差值/m213.210.135 121.86 0.131 9.54 0.150 0.066 0.065 0.001 203.210.135 123.35 0.127 9.27 0.150 0.075 0.065 0.010 213.010.135 122.57 0.130 9.27 0.145 0.062 0.055 0.007 193.010.135 121.96 0.127 9.27 0.146 0.053 0.055 0.002
由表4可知,上浮量差值最大值为0.01 m,误差为13%,所有计算结果的平均误差约为7%。
由表4可知,随着布放深度的增加,上浮量变化不明显;布放深度对上浮量的影响作用不大,产生此种情况的原因一是由于布深量值变化不大,只有0.2 m,与静压相当深度10.3 m比较为小量,在本试验条件下布深变化量较小,布深对上浮量变化基本可忽略。考虑边界条件的影响,主要是底部吸引作用,计算上浮量与测量上浮量最大差值为0.01 m,此种工况下计算结果误差为8.3%。
6 结论
通过研究,得到以下结论:
1) 根据无限水域无量纲上浮量和周期之间对应的正比例关系,推导得到气泡脉动上浮量和测量周期之间对应关系,得到基于测量周期的上浮量计算公式。
2) 自由场情况(无限水域)下,由气泡脉动周期测量值计算得到水下爆炸气泡上浮量,并同理论值进行比较。结果表明,两者量值差别不大。越靠近底部,误差越大,主要原因是由于底部的存在,使气泡上浮量变小,使气泡脉动周期变大,两者变化趋势不一致。
3) 根据气泡上浮量计算结果、冲击波峰值压力对应测量距离,求得第1次气泡脉动峰压值对应的距离,进而求解得到气泡脉动峰值;然后同气泡峰压测量值进行比对,得到气泡脉动峰压值的比例系数,对于TNT装药而言,修正系数平均值为0.62。
4) 气泡脉动峰值测量结果偏大的主要原因是由于空化导致,一方面,冲击波负压导致流场发生一定的变化,空化更容易形成;另一方面,水表面空化溃灭载荷叠加,也可能是受水面或水底等边界影响,气泡收缩膨胀转换时压力波的释放有所改变。
5) 对气泡脉动压力峰值进行修正,结合冲击波峰值压力对应距离,计算得到上浮量,并同理论值进行比较;平均误差为3.68%,误差值在允许范围内。
6) 提出了气泡上浮量修正模型,考虑边界条件对上浮量的影响,对自由场情况下的计算模型进行修正,并将计算结果与小药量测量结果进行比较分析。计算上浮量与测量上浮量最大差值为0.01 m,与最大气泡半径比为小量。
[1] COLE R H.Underwater explosion[M].Princeton: Princeton University Press,1948:260-360.
[2] 张阿漫.水下爆炸气泡三维动态特性研究[D]. 哈尔滨:哈尔滨工程大学,2007.ZHANG Aman.Reseach on three-dimension dynamics of underwater explosion bubbles[D]. Harbin :Harbin Engineering University,2007.
[3] 姚熊亮,汪玉,张阿漫.水中爆炸气泡动力学[M]. 哈尔滨:哈尔滨工程大学出版社,2012:22-76.YAO Xiongliang,WANG Yu,ZHANG Aman.Shuixia baozha qipaodonglixue[M].Harbin:Harbin Engineering University Press,2012:22-76.
[4] CRISTOV E B.Cavitation and bubble dynamics [M].Zhenjiang:Jiangsu University Press,2013:33-64.
[5] 张弩,宗智.水下爆炸气泡载荷对舰船的总体毁伤研究 [J].中国造船,2012,53(3):28-39.ZHANG Nu,ZONG Zhi.Global damage of ship hull subjected to underwater explosion bubble loading [J].Shipbuilding of China,2012,53(3):28-39.
[6] 秦健,艾东民,吴成,等.几种炸药水下爆炸能量损失特性分析研究[J].兵工学报,2015,36(2):38-42.QIN Jian,AI Dongmin,WU Cheng, et al.Research on energy dissipation characteristics of explosion[J].Acta Armamentarii,2015,36(2):38-42.
[7] 张永坤. 水下爆炸气泡运动稳定性分析研究[J].舰船电子工程,2022,42(6):171-176.ZHANG Yongkun.Research on stability analysis of the underwater explosion bubble[J].Ship Electronic Engineering,2022,42(6):171-176.
[8] 黄毅,张弩.水下爆炸气泡脉动载荷影响因素分析[J].中国舰船研究,2013,8(6):33-39.HUANG Yi,ZHANG Nu.Analysis of the impact parameters of the bubble pulsation load in underwater explosion[J].Chinese Journal of Ship Research,2013,8(6):33-39.
[9] 任松涛,郭炜.炸药水中爆炸气泡脉动冲量试验研究[J].科学技术与工程,2017,17(13):173-176.REN Songtao,GUO Wei.Experimental study of bubble impulsion induced by underwater explosion [J].Science Technology and Engineering,2017,17(13):173-176.
[10] 汪斌,王彦平,张远平.有限水域气泡脉动试验方法研究[J].火炸药学报,2008,31(3):32-35.WANG Bin,WANG Yanping,ZHANG Yuanping.A method of studying bubble pulses in a confined water area[J].Chinese Journal of Explosion and Propellants,2008,31(3):32-35.
[11] 汪斌,张远平,王彦平.一种水中爆炸气泡脉动试验研究[J].高压物理学报,2009,23(5):332-337.WANG Bin,ZHANG Yuanping,WANG Yanping.An experimental method of studying underwater explosion bubble[J].Chinese Journal of High Pressure PhysicsResearch,2009,23(5):332-337.
[12] 朱锡,牟金磊,洪江波,等.水下爆炸气泡脉动特性的试验研究[J].哈尔滨工程大学学报,2007,28(4):365-368.ZHU Xi,MOU Jinlei,HONG Jiangbo,et al.Experimental study of characters of bubble impulsion induced by underwater explosions[J].Journal of Harbin Engineering University,2007,28(4):365-368.
[13] 张颖,赵生伟,王占江,等.水下爆炸气泡脉动测量及分析[J].试验力学,2011,26(1):67-72.ZHANG Ying,ZHAO Shengwei,WANG Zhanjiang,et al.Mearemet and analysis of characters of bubble impulsion induced by underwater explosions[J]. Journal of Experimental Mechanics,2011,26(1):67-72.
[14] 盛振新,刘建湖,张显丕,等.水下爆炸气泡射流载荷阵列测量技术探索[J].爆炸与冲击,2021,41(3):55-62.SHENG Zhenxin,LIU Jianhu,ZHANG Xianpi,et al.On an array-sensor technology for measuring bubble jet load generated by underwater explosion[J].Explosion and Shock Waves,2021,41(3):55-62.
[15] 王振雄,顾文彬,陈江海,等.浅水中爆炸水底介质对水中冲击波峰值压力影响的试验研究[J].振动与冲击,2017,36(4):243-248.WANG Zhenxiong,GU Wenbin,CHEN Jianghai,et al.Experimental study on the influence of thebottom medium on the peak pressure of explosion shock waves in shallow water[J].Journal of Vibration and Shock,2017,36(4):243-248.