0 引言
在众多领域中,系统的可靠性评估一直是一个备受关注的课题。在系统生命周期内,系统通常包含多种不同的操作任务,每个任务都具有独特的要求、目标和环境,这使得系统的可靠性评估变得非常困难。任务剖面是一种常用于描述系统的工作任务和操作的重要工具,可以对系统寿命周期内所有相关的运行条件进行描述[1-3]。通常一个复杂系统可以划分为多个任务剖面,为了更准确地评估复杂系统的可靠性,必须综合考虑这些任务剖面。
过去以多任务剖面为核心的系统可靠性研究取得了显著的进展,这些研究从不同领域出发,在多任务建模方法[4-7],任务之间的依赖性[8-10],时段延续性[11-12],多任务阶段组件失效[13-14]等方面建立了系统可靠性模型,并对各自的复杂系统进行可靠性评估。比如:刘震宇等[15]针对作战飞机故障数据的特点,分析了作战飞机不同飞行剖面对任务可靠性的影响,结合飞行剖面折合系数、建立了作战飞机任务可靠性模型。周思醒等[16]针对传统舰船总体任务可靠性建模方法难以全面反映舰船的实际任务的问题,提出舰船单元任务的概念,通过拆分单元任务,以多任务剖面的方式计算舰船总体的可靠性。吕建伟等[17]对海军舰艇分多个任务阶段,分析了各阶段任务之间的关系以及装备故障的严重性及其影响,提出处理方法并计算出舰船综合任务可靠性;闫华等[18]介绍了基于Markov进行分阶段建模方法,总结了基于Markov的任务可靠性模型求解方法;Wang等[19]针对无人机群多层任务之间的依赖性建立无人机群的多层网络模型,并在此模型基础上提出一种脆弱性和连接性的评估方法用于无人机群任务可靠性建模与评估;王刚[20]将一个分任务阶段的TTC 系统分为多个任务剖面,运用二元决策图(BDD)描述多任务阶段存在的动态性和依赖性,完成了系统可靠性分析;谢红卫等对于多阶段系统中出现的一种不能分阶段单独处理的问题,引出时段延续相关性理论,提出了有效的解决方法并建立了相应的数学模型。这些研究为复杂系统的多任务剖面建模和可靠性评估提供了有价值的参考和方法。
虽然上述国内外学者从多个领域,多个角度对复杂系统进行可靠性建模与评估,并取得了较多的研究成果,但遗憾的是目前尚未有学者考虑以下几个方面:① 对于系统进行可靠性研究时未考虑组件的连接方式,或者仅考虑串并联结构,而大型设备的组件数量多,或包含表决及冗余结构,因此从含有表决模型的混联系统层面上出发,研究设备多任务剖面下的评估更具有意义。② 任务剖面转换时,任务要求不同导致故障判据也不同,多任务系统可靠性逻辑结构也会发生改变,组件数量随之发生改变,系统中所包含的组件并不是在任意剖面下均参加工作,待工作组件在环境的影响下也会发生故障[19],此故障虽然不会对该任务剖面产生影响,但是对于下一次有该组件参加工作的任务剖面会造成无法预知的影响,因此有必要考虑待工作组件的故障对综合系统造成的影响。③ 待工作组件故障会有多种状态,考虑待工作组件的故障状态可以有效地评估和提高系统的可靠性,避免造成误差。
鉴于此,针对任务剖面转换时,系统逻辑结构发生改变和任务剖面间待工作组件故障的相关性带来的问题,本研究中以复杂系统中常见的表决混联系统作为研究对象,建立含有表决模型的多任务剖面可靠性模型,分析在多任务剖面条件下待工作故障相关性对整体系统可靠性的影响,通过动态贝叶斯网络对待工作故障时变运行状态进行建模,利用蒙特卡洛估计法评估系统的可变参数对动态系统可靠性的影响。最后通过算例分析,验证了所提方法的合理性。
1 多任务剖面下混联系统可靠性建模
首先建立系统在一个任务剖面下的可靠性模型,以常见的表决模型形式为例,假设该剖面中含有m个A组件,一个A组件连接若干个B组件,为方便计算,本例中统一连接δ个B组件,可靠性框图如图1所示。
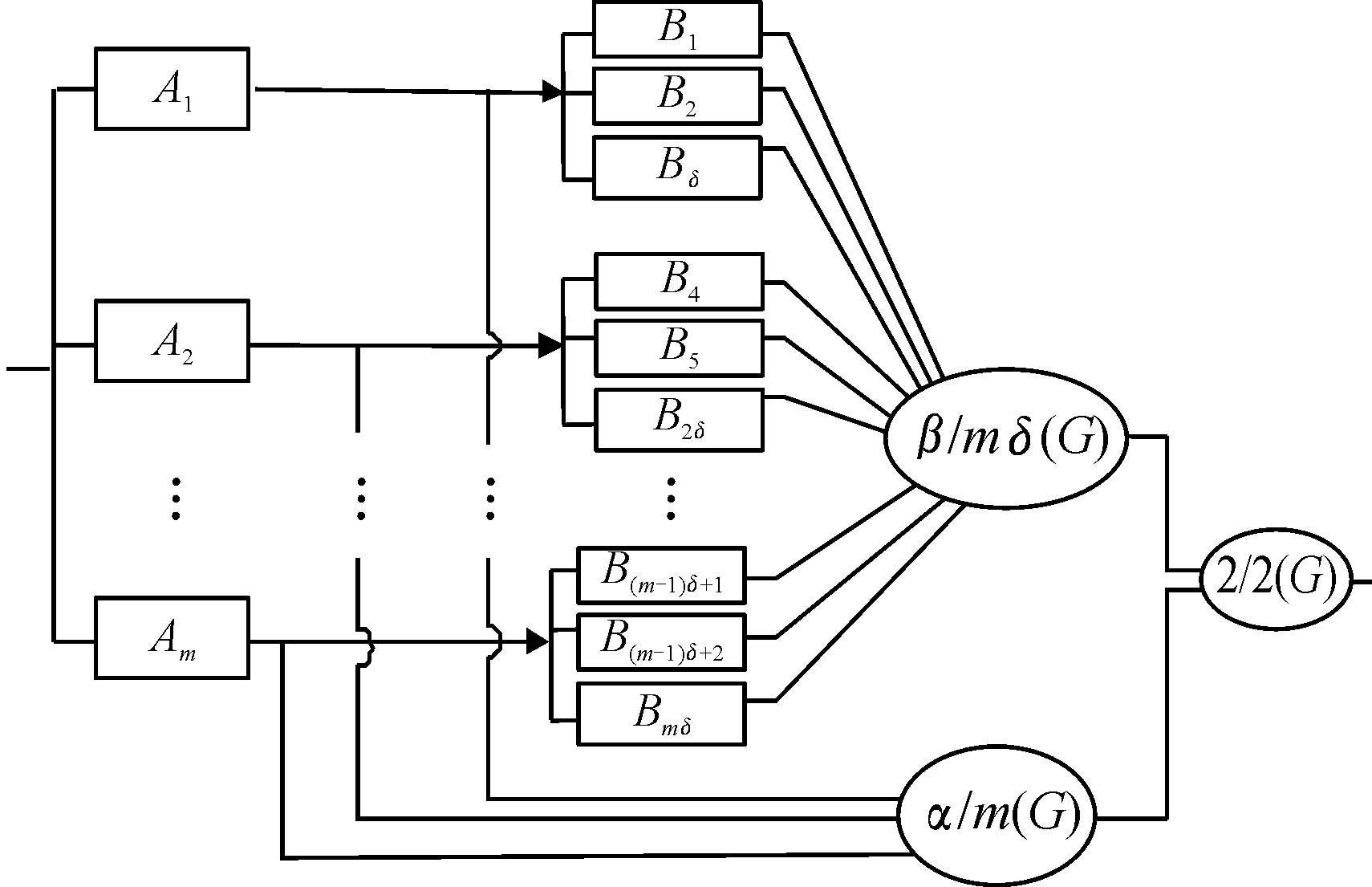
图1 某任务剖面下的可靠性框图
Fig.1 Reliability diagram under a task profile
由图1可知,A组件集合形成了决策模型α/m(G),α为该模型正常工作时的最小表决数, A组件通过与B组件连接后,又形成了决策模型β/δm(G), β为该决策模型正常工作时的最小表决数。
针对多任务系统,仅单个任务剖面无法提供系统的全面时序描述。这是由于不同的任务剖面涉及不同的组件工作以及组件工作数的多样性。因此,考虑采用多任务剖面对系统进行可靠性建模,如图2所示。

图2 多任务剖面条件下的系统可靠性框图
Fig.2 Reliability diagram of a system under multiple task profile conditions
图2中,任务剖面1决策模型为α1/m(G)和β1/δm(G);假设任务剖面2有任务剖面1中组件A和组件同样的连接方式,但是有n组A组件连接δn组B组件(其中n=m+q),决策模型为α2/n(G)和β2/δn(G),对于第k个任务剖面,组件A的个数为pk,组件B的个数为qk,组件之间的连接方式用(pk,qk)表示,则初始状态的可靠性模型为

(1)
式(1)中:R1为任务剖面1下的可靠度;R2为任务剖面2下的可靠度;Rk为任务剖面k下的可靠度;k为系统的任务数。
由于每个任务剖面涉及的工作组件数量各异,这给系统的可靠性评估带来了挑战。工作组件可能会因载荷应力、环境变化而发生故障,对可靠性产生显著影响。同时,待工作组件也可能会受到外部环境的影响而出现故障。因此,为了提高可靠性评估结果的准确性,有必要同时考虑任务剖面之间的相关性以及其对系统可靠性的影响。
2 考虑待工作组件故障的可靠性建模
2.1 基于动态贝叶斯网络的故障多状态分析
动态贝叶斯网络可以将贝叶斯网络结构与时间序列结合[20],采用动态贝叶斯网络对待工作组件故障在含有表决模型的多任务剖面间的建模工作进行分析。将设备中的待工作组件视为根节点,将待工作组件的故障状态进行分级,即为正常状态(Z),故障衰减状态(S),严重故障状态(Y),则根节点存在以上3种状态。当处于故障衰减状态时,该组件并不会影响系统的运行,但是存在一定的安全隐患;处于严重故障状态时,该组件会对下一任务剖面造成严重的影响,甚至会导致系统无法运行。根节点之间存在转换关系,当组件发生严重故障状态时,考虑更换该组件,使系统恢复正常状态。在动态贝叶斯网络中根节点的状态转移过程如图3所示,状态转移关系如表1所示,其中λ为状态转移过程中的失效率,μ为维修率。
表1 节点状态转移关系
Table 1 Node status transition relationship

节点状态t时刻t+Δt时刻转移概率ZSλ1(λ1+λ3)-1(1-e-(λ1+λ3)Δt)ZYλ3(λ1+λ3)-1(1-e-(λ1+λ3)Δt)SY1-e-λ2ΔtYZ1

图3 根节点状态转换图
Fig.3 Root node state transition diagram
根据待工作故障随时间变化而导致的故障状态转移关系,建立各故障状态转移下的可靠性模型。假设任务剖面之间的待工作组件有A组件和B组件,记A组件和B组件的可靠度为RA和RB,可知当组件由正常状态转为故障衰减状态时:
![]()
(2)
组件由正常状态转为严重故障状态时:
![]()
(3)
组件由故障衰减状态转为严重故障状态时:
![]()
(4)
式(2)中:RA(t)为待工作组件A的可靠度; RB(t) 为待工作组件B的可靠度。
观测待工作组件的状态转移,当组件发生严重故障时,对损坏的组件进行更换,可使该部分组件的可靠度可恢复至正常状态。进而为后续考虑待工作组件多状态下的可靠性建模提供输入。
2.2 考虑待工作组件故障多状态下的多任务剖面可靠性建模
由于不同任务剖面的工作时间和工作组件存在差异,任务剖面间的待工作组件受到电磁、温度、湿度、振动等外部环境的影响而发生一定程度的故障。这些故障不仅会对当前任务剖面的执行造成影响,而且还会对后续任务剖面的执行产生延续影响。针对这种故障的延续影响,可以依次分析每个任务剖面之间的待工作组件故障情况。
首先不考虑待工作组件故障对于系统可靠性的影响,建立系统最初的可靠性框图和仿真评估流程,然后在此基础上再进行考虑待工作组件故障对于系统可靠性影响的分析。如图4所示,剖面1到剖面2之间有(n-m)A+(δn-δm)B个组件在剖面1下属于待工作状态。剖面1从t=0时刻开始,到t=t1时刻结束;剖面2从t=t1时刻开始,到t=t2时刻结束。当t=0时,系统可靠性仿真流程还是原始状态;当0<t<t1时,对工作的m个A组件和δm个B组件进行工作故障影响下的分析,对(n-m)A+(δn-δm)B个还未工作但将要在下一个任务剖面中工作的组件进行可靠性影响分析。初始的可靠性评估流程并未考虑待工作组件发生了故障,认为组件性能完好,如果此时待工作组件发生故障,则初始评估流程就会存在误差,为了解决这种误差,建立考虑待工作组件故障后的可靠性评估模型,即:
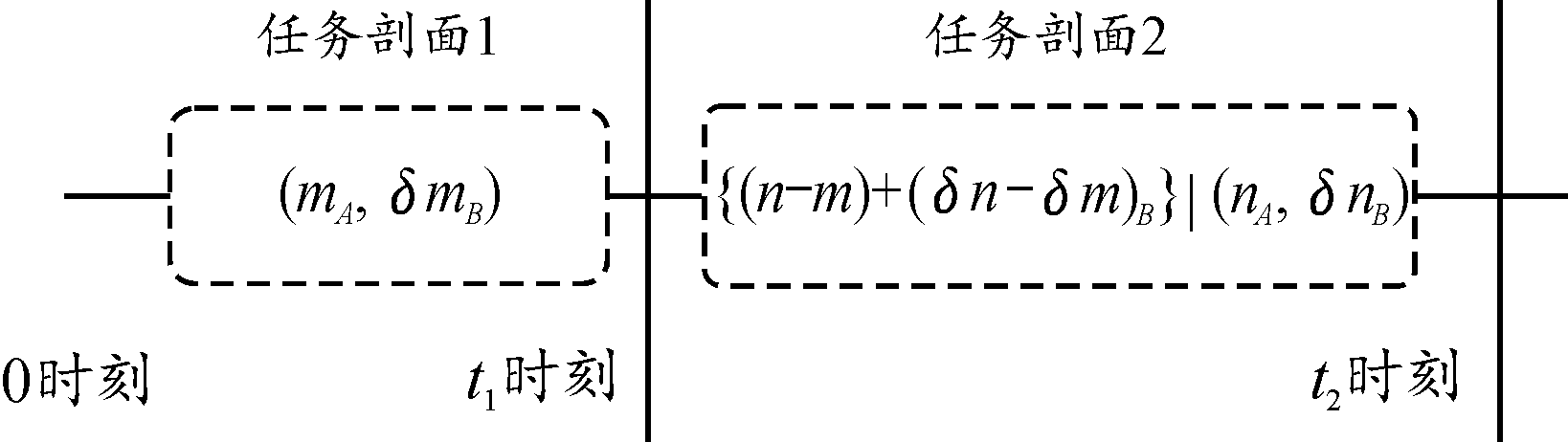
图4 任务剖面间待工作故障延续性分析示例
Fig.4 Example of non working fault continuity analysis between task profiles
![]()
(5)
式(5)中:R1为任务剖面1下的可靠度;R2为任务剖面2下的可靠度;R(1)A为任务剖面1与任务剖面2间待工作组件A的可靠度;R(1)B为任务剖面1与任务剖面2间待工作组件B的可靠度。
因此,对于有k个任务剖面的电子系统,建立考虑任务剖面间的待工作组件多状态下的可靠性评估模型为

(6)
式(6)中:R(k-1)A为任务剖面k-1与任务剖面k间待工作组件A的可靠度;R(k-1)B为任务剖面k-1与任务剖面k间待工作组件B的可靠度;Rk-1为任务剖面k-1下的可靠度;Rk为任务剖面k下的可靠度;k为系统的任务数。
3 多任务混联系统的可靠性综合评估
以图2所示的多任务剖面下的可靠性模型为例,对系统可靠性评估工作进行分析。在该表决模型中决策模型2/2(G)在效果上等效为串联模型。在不考虑A组件与B组件之间的相互影响时,决策模型α1/m(G)和决策模型 β1/δm(G)的可靠度分别为

(7)
任务剖面1的可靠度为
![]()
(8)
通常情况下,A组件故障也会导致对应干路上的δ 个B组件失效,考虑到A组件和B组件之间的影响关系,则任务剖面1的可靠度为

(9)
式(7)中:α1为决策模型α1/m(G)正常工作的最小组件数,m为组件总数; β1为决策模型β1/δm(G)中正常工作的最小组件数,δm 为组件总数, RGAB_1为任务剖面1的可靠度。
同理,任务剖面2的可靠度为

(10)
式(10)中:α2为决策模型α2/m(G)正常工作的最小组件数,n为组件总数;β2为决策模型β2/δn(G)中正常工作的最小组件数,δn为组件总数, RGAB_2为任务剖面2的可靠度。
式(10)中RGAB_2未考虑待工作故障延续性,此时对n-m个非工作状态的组件进行评估。待工作的故障模式与工作状态的故障模式不同,待工作时的A组件和B组件的可靠度为RA*和RB*。在任务剖面1中,系统满足α1/m(G),β1/δm(G)和2/2(G)的判决条件,在任务剖面2中,系统满足α2/n(G),β2/δn(G)和2/2(G)的判决条件,为了确保任务剖面1下的待工作组件不会影响到任务剖面2的正常工作流程。则任务剖面1的系统待工作模块需满足:α2-α1/n-m(G), β2-β1/δn-δm(G)。
已知,A组件和B组件在待工作组件衰减状态时的失效率为λA1*,λB1*,结合待工作组件在多种状态转移概率下的可靠性模型,可知A、B组件由正常状态到故障衰减状态的可靠度为
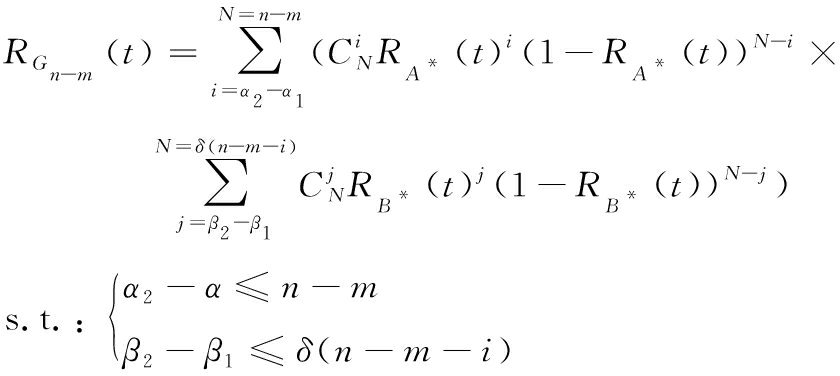
(11)
A、B组件由正常状态到严重故障状态的可靠度为
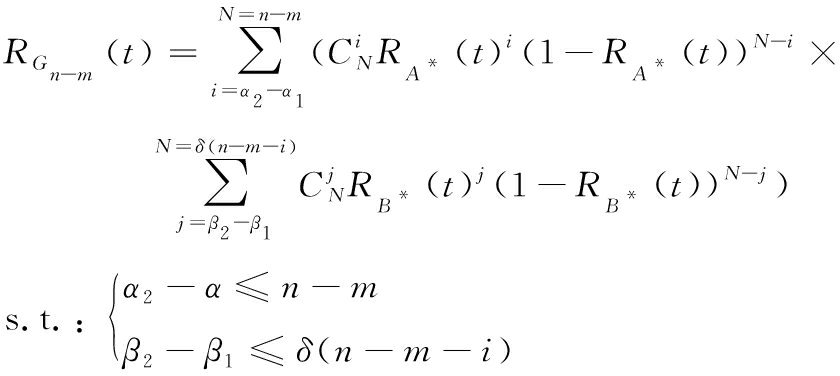
(12)
A、B组件由故障衰减状态到严重故障状态的可靠度为

(13)
同理任务剖面k下的可靠性评估需要首先根据系统的任务判据对组件进行可靠性建模,然后进行可靠度计算。系统会根据任务顺序依次进行工作,完成第一个任务剖面下的任务后,设备才会进入下一个任务剖面进行工作,在每个任务剖面下对系统可靠性进行评估,已知可靠度R(t)随着时间的增加具有递减趋势,因此系统综合可靠度为
R综=min{RP1,RP2,…,RPk}
(14)
式(14)中:RP1为第1个任务剖面结束时的可靠度;RP2为第2个任务剖面结束时的可靠度;RPk为第k个任务剖面结束时的可靠度。
该方法对于含有表决模型的多任务剖面下的可靠性评估工作具有一定的通用性,这主要体现在建模方法与分析方法上,针对含有表决模型的多任务系统,该方法可以辅助完成多任务剖面的可靠性建模,并获得系统综合可靠性结果;在实际工程中,对于含有表决模型的可靠性评估,可以根据工程情况设置对应的δ、α、β的数值;基于动态贝叶斯网络对多任务剖面条件下考虑待工作组件故障延续性的可靠性建模与评估分析,有助于更准确地获取系统的可靠度。
4 案例分析
以某雷达天线系统为例进行混联系统可靠性建模与评估。已知雷达天线系统具有3个任务,雷达天线中含有定时模块,DBF模块,频综组件,电源组件与TR组件,组件数量如表2所示。
表2 雷达天线模块(组件)名称及数量
Table 2 Name and quantity of radar antenna module (assembly)

名称数量/个名称数量/个定时模块1频综组件1DBF模块1电源组件16TR组件256
系统分为串联区域与表决区域,两区域之间串联。串联区域连接方式如图5所示。
图5 雷达天线系统串联区域可靠性框图
Fig.5 Reliability diagram of series region of radar antenna system
表决区域中一个电源组件连接16个TR组件,即δ=16,其中16个TR组件之间并联,电源组件之间并联。该电子系统可靠性框图如图6所示。
图6 雷达天线系统任务剖面可靠性框图
Fig.6 Reliability diagram of radar antenna system task profile
系统的3个任务剖面之间的工作组件差异主要表现在表决区域,各任务剖面的工作组件数和待工作组件数如表3所示。
表3 任务剖面工作组件数与待工作组件数量
Table 3 Number of working components and number of components to be worked in the task profile

任务剖面α/m(G)β/3m(G)待工作组件111/13(G)176/208(G)-1-2--1(电源)+16(TR)212/14(G)192/224(G)-2-3--2(电源)+32(TR)312/16(G)192/256(G)-
根据系统的任务判据分别建立任务剖面下的可靠性框图。由表可知,3个任务剖面中工作的组件数并不相同,因此对雷达天线系统进行可靠性评估不仅要考虑工作组件故障影响,同时也要考虑待工作组件故障在任务剖面之间的延续性,提高天线系统综合可靠性评估精度。
同一个任务剖面下,不同组件故障模式也存在一定的差异。根据故障机理竞争原则,已知各个模块受到影响最大的故障模式,以及它们所对应的故障机理模型,如表4所示。
表4 各模块(组件)的主要故障模式以及故障机理模型
Table 4 The primary fault modes and fault mechanism models of each module (component)

模块名称主要故障模式故障机理模型定时模块电性能失效电迁移模型MTTF=WdTmCjnexpEakT DBF模块电性能失效电迁移模型MTTF=WdTmCjnexpEakT 频综组件短路Eyring模型Tf=Ke-(0.13)RHe35 700RT电源组件电性能失效修正Coffin-Manson模型Δεp2=εf(2Np)cNcr=CΔγcr1Nf=1Np+1NcrTR组件氧化层缺陷Wu模型TTFE=Aexp(γE)expEa1kT
已知各模块(组件)中的参数并不全是确定的数值,比如电迁移模型中的电流密度J(A/m2)和Eα(eV),Eyring模型中的相对湿度函数RH,Coffin-Manson模型中的温度变化幅值ΔT(K),Wu模型中加在栅氧化层上的电场强度E(V/m)等,假设以上参数服从正态分布,这里的数值为工程中各模块(组件)常使用的均值与方差数值,用以验证本文方法的正确性。
针对故障机理模型中存在不确定参数造成评估工作困难的问题,采用蒙特卡洛法对不确定参数进行抽样,计算出每个组件的故障前时间。具体步骤如下:
步骤1:对系统和仿真进行初始化处理,获取模型中所有的参数数据信息,设置仿真次数N;
步骤2:根据不确定参数的分布,计算出每个模块的故障前时间,组件的故障前时间是对组件影响最大,使组件无故障运行时间最短的故障所决定,记为TM;
步骤3:通过抽样仿真获取组件的故障前时间,即组件的寿命分布,判断是否达到规定的仿真次数,若否,则回到步骤2;
步骤4:设置可靠性指标要求,对该组件的寿命进一步的分析,统计出达到可靠性指标要求的可靠次数Nr;
步骤5:在t时刻,组件的可靠度为![]() 不可靠度为
不可靠度为![]()
利用蒙特卡洛抽样法得到定时模块,DBF模块,频综组件,电源组件,TR组件的寿命分布直方图,如图7—图11所示。
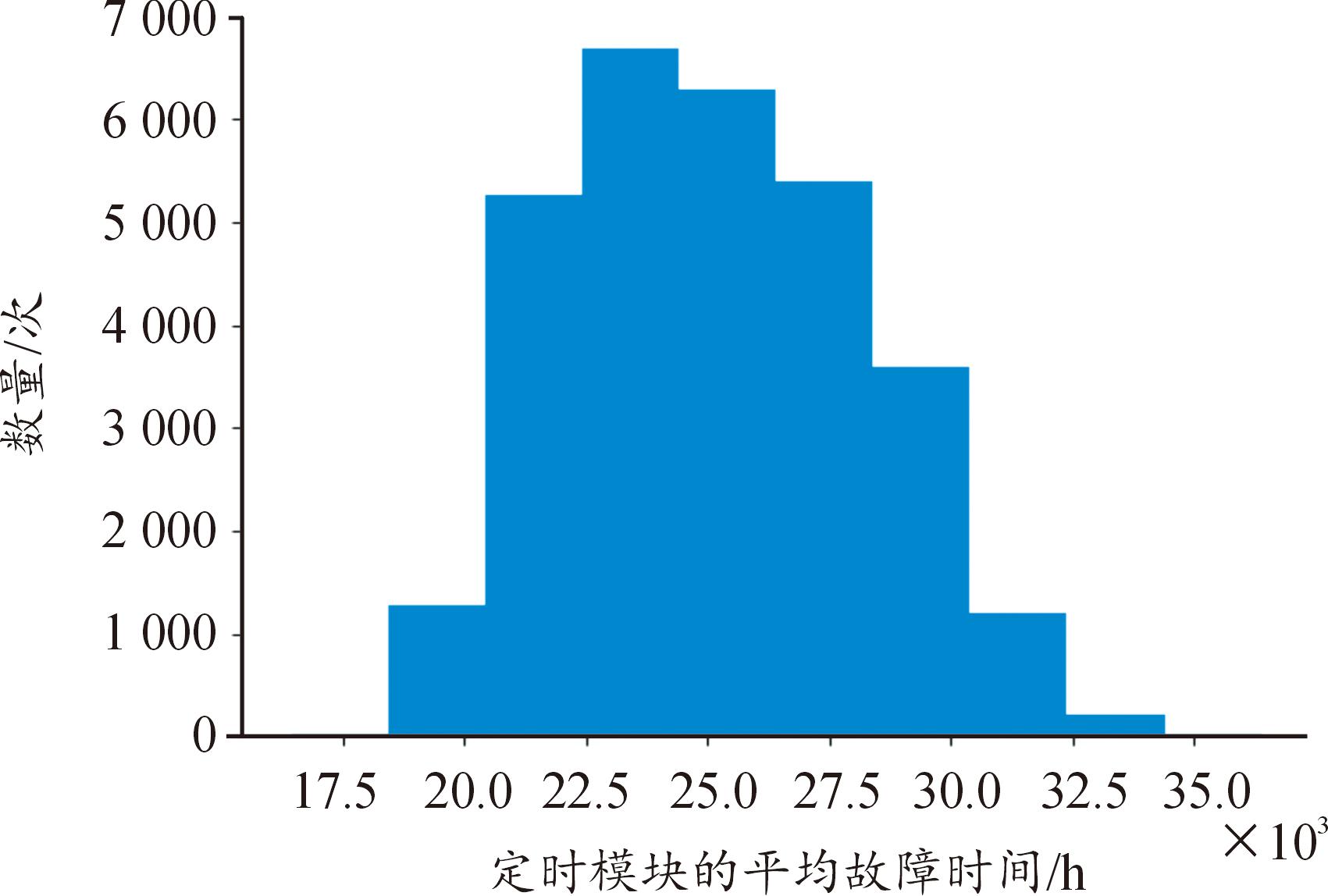
图7 定时模块寿命分布直方图
Fig.7 Lifetime distribution histogram of timing module
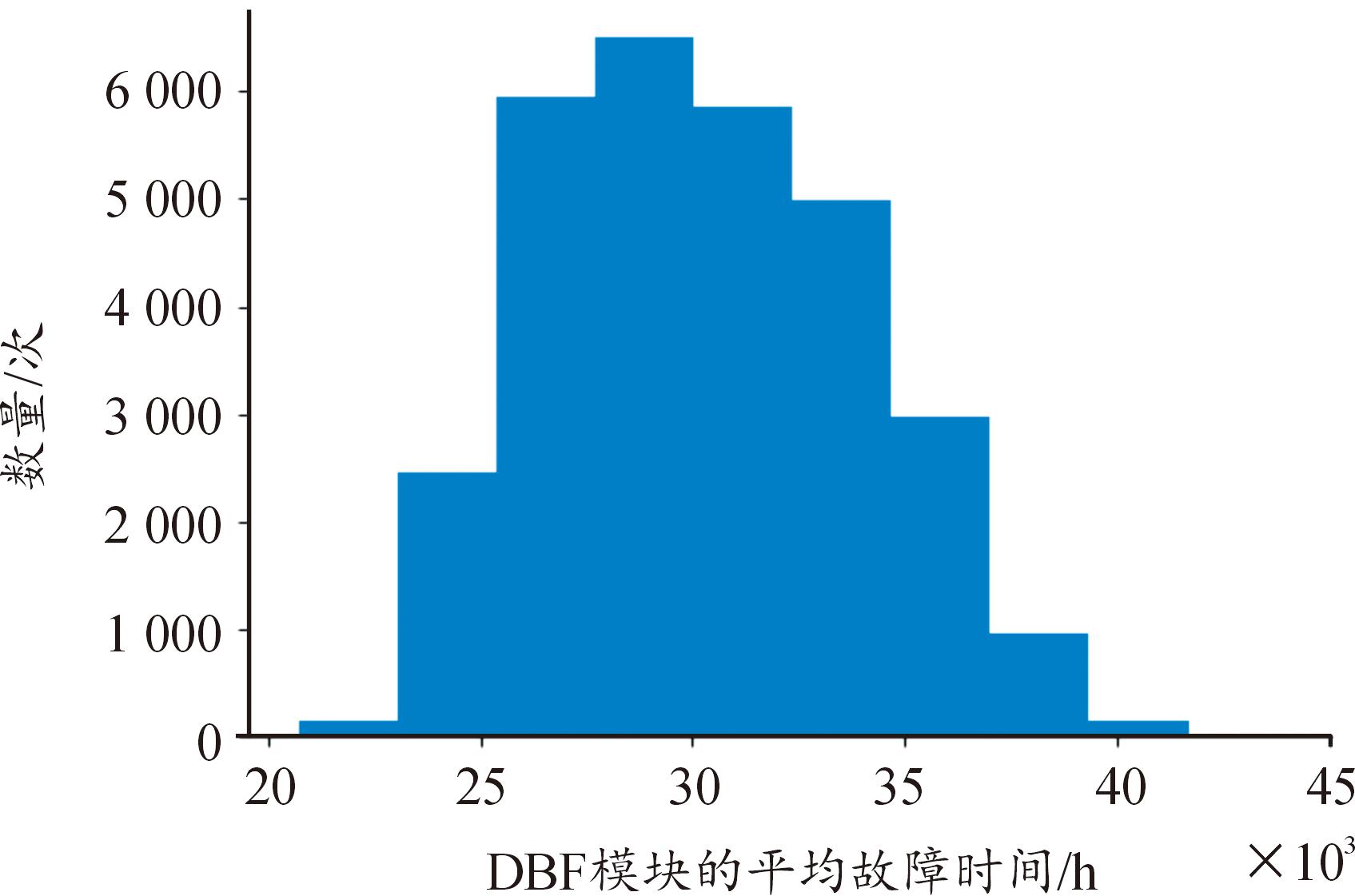
图8 DBF模块寿命分布直方图
Fig.8 Life distribution histogram of DBF module
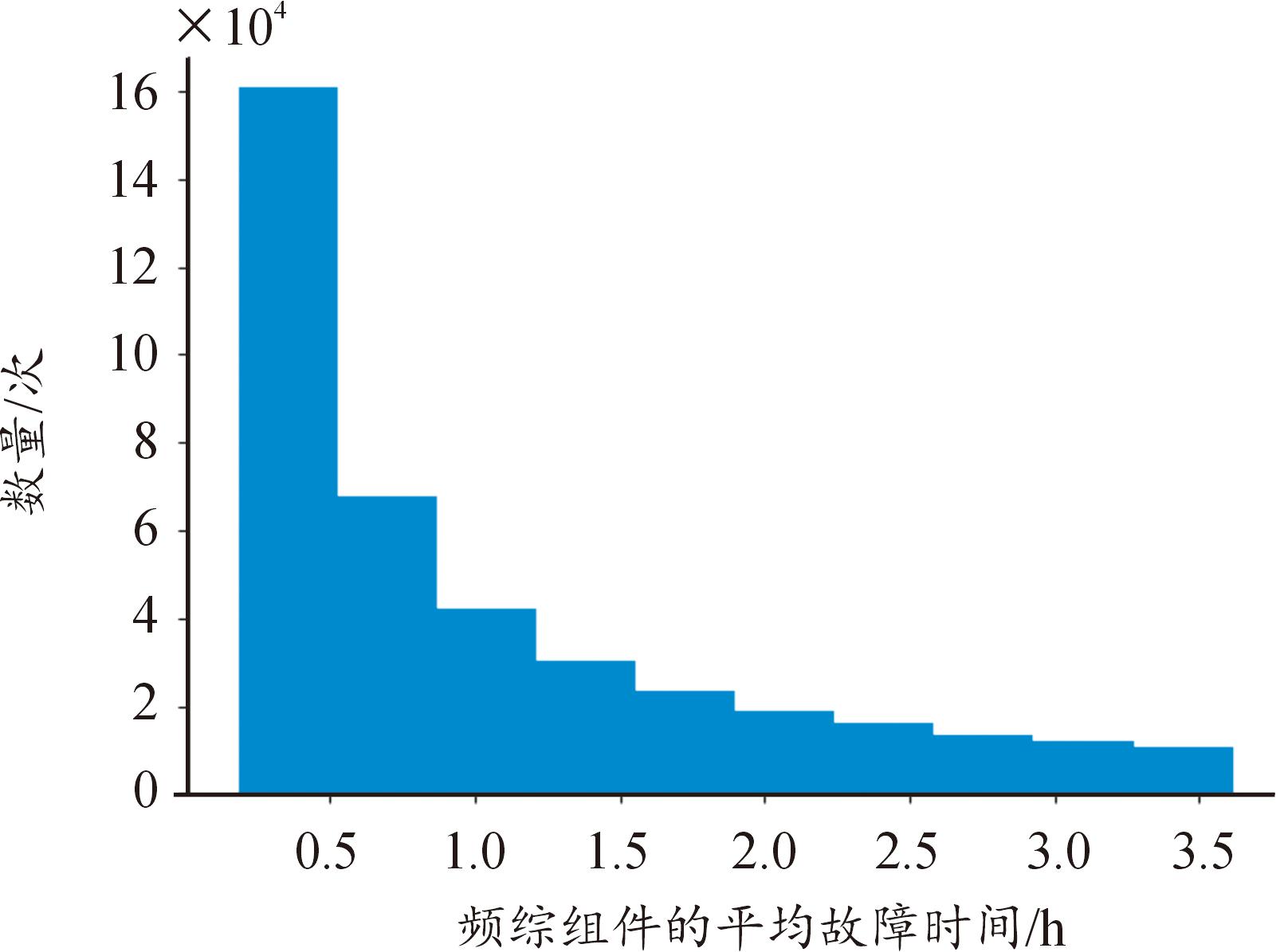
图9 频综组件寿命分布直方图
Fig.9 Life distribution histogram of frequency synthesizer assembly
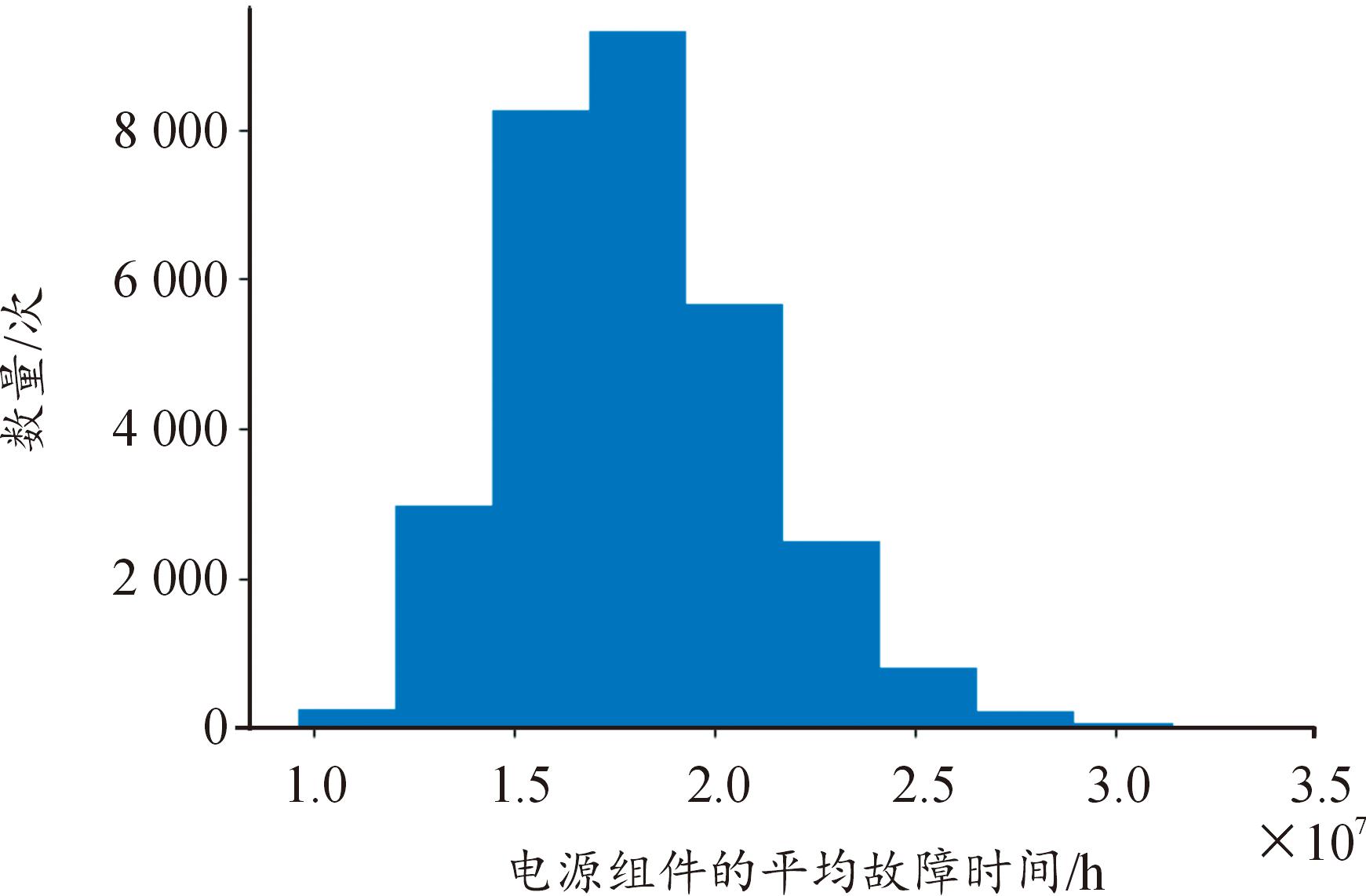
图10 电源组件寿命分布直方图
Fig.10 Power supply component life distribution histogram
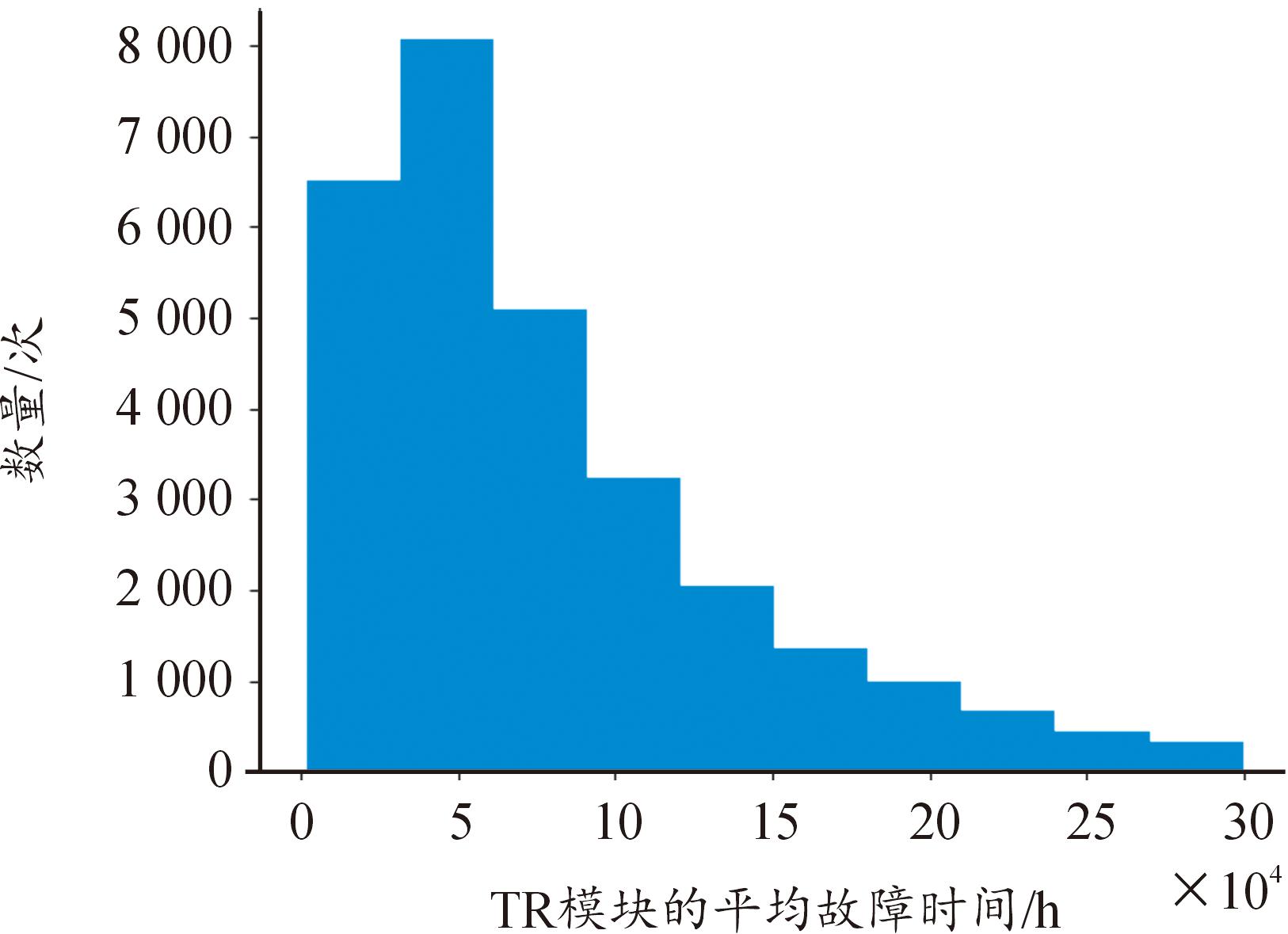
图11 TR模块寿命分布直方图
Fig.11 TR module life distribution histogram
假设在此工作环境下进入下一任务剖面时,组件受影响最大的故障模式保持不变。已知在各任务剖面下的组件数量,根据不同任务剖面下可靠度的求解公式得到多任务剖面条件下只分析工作故障影响的可靠度变化趋势,如图12所示。

图12 多任务剖面条件下工作故障影响的可靠度变化趋势
Fig.12 Variation trend of reliability affected by operation failure under multi task profile
在该雷达系统中,当待工作组件处于正常状态时,对下一任务剖面并不会造成影响;当待工作组件接近故障状态时,考虑及时更换故障组件,避免系统发生故障带来更大的影响;因此本研究中只考虑待工作组件由正常状态到故障衰减状态,已知电源组件在受到电磁干扰时的故障衰减状态下故障率为1.535×10-6 fit,TR组件在受到电磁干扰时的故障衰减状态下的故障率为2.328×10-6 fit,根据考虑待工作组件故障部分的可靠度公式可以得到在任务剖面1中,待工作组件受到故障影响下的可靠度变化趋势,如图13所示。
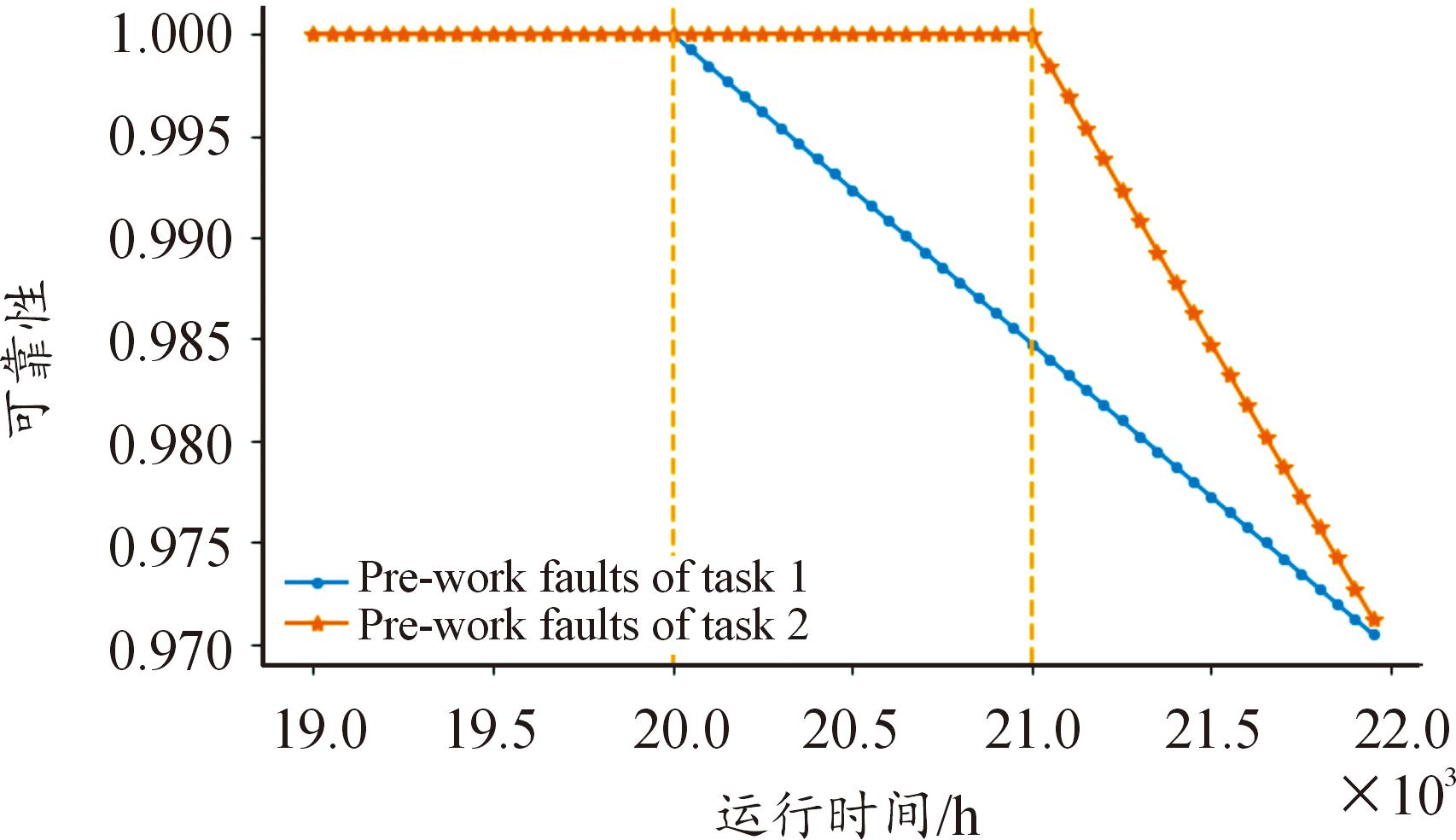
图13 待工作组件故障的可靠度变化趋势
Fig.13 Trends in reliability of pending component failures
由图13可知,待工作组件在任务剖面1开始的一段时间是一直处于正常状态,随着工作环境中各种载荷、应力的影响,待工作组件也发生了相应的故障,导致这些待工作组件还未开始工作就出现了可靠性下滑的趋势,考虑待工作组件故障影响对于可靠性评估更具有实际意义。
此时对雷达装备系统进行综合可靠性评估。在任务剖面1中,部分电源组件和TR组件会受到工作故障的影响,随着工作时间的推移,观察此时系统可靠度变化趋势,此时剩余部分的电源组件和TR组件受外部环境的影响,也发生了待工作故障,但目前这些组件即使发生了故障,对系统的可靠性也没有影响。进入任务剖面2时,之前的待工作组件开始进入工作状态,如果之前的待工作组件因为故障受损,此时组件的运行情况就会对系统的可靠性评估结果造成一定的影响。此时,不仅要考虑这些组件受到了待工作故障的影响,还要考虑组件处于不同的运行状态时系统可靠性的变化情况,故对系统进行综合可靠性评估时考虑了参数不确定及待工作故障影响等各种动态因素后的可靠度变化情况如图14所示。
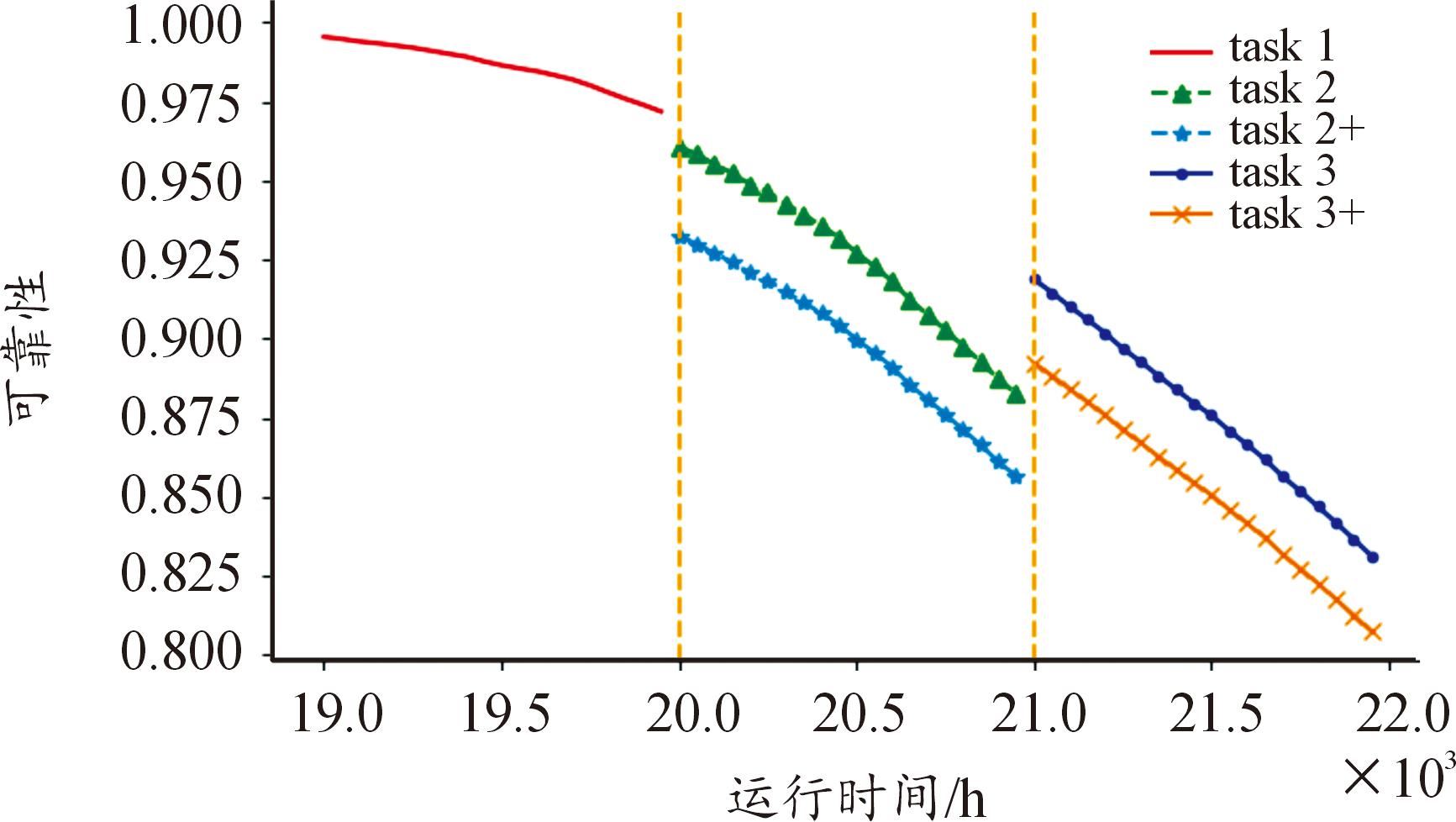
图14 多任务剖面条件下考虑待工作组件故障的可靠度变化趋势及对比
Fig.14 Trend and comparison of reliability changes considering component failures under multitask profile conditions
通过以上故障影响分析过程,得知待工作组件在待工作环境影响下的系统可靠度的变化趋势。任务剖面1中的待工作组件发生故障后,剖面1的可靠度并不会发生变化,但是由于组件已发生一定的损坏,进入任务剖面2时,可靠性就会出现相对于不考虑待工作故障可靠性降低的情况。
在多任务剖面条件下,不仅要考虑工作组件的故障影响,也要考虑待工作组件的影响,待工作组件处于不同的状态对系统可靠性的影响也不同:待工作组件处于正常状态时,系统可靠度不受影响;待工作组件由正常状态转为故障衰减状态时,待工作组件故障会对系统可靠性造成影响,观察系统可靠性指标变化趋势,更加准确地得到该故障对系统可靠性的影响程度,从而提高了多任务剖面条件下系统可靠性评估的精度;待工作组件由正常状态转为严重故障时,在进入下一任务剖面前将故障组件进行更换,以免对设备造成更加严峻的影响。然后分别得到系统在不同任务剖面下的可靠性指标,继而完成雷达设备电子系统的综合可靠性评估。
5 结论
针对复杂系统组件数量众多、组件连接关系复杂等特点,以含有表决模型的混联系统为研究对象,考虑到混联系统多任务剖面转换时可靠性逻辑结构发生改变,建立了多任务剖面的系统可靠性模型。该模型针对逻辑结构发生改变带来的工作组件数量不一致、待工作组件发生故障、故障多状态以及故障延续性等问题,提出了基于动态贝叶斯网络的可靠性建模与评估方法,并得出以下结论:
1) 该方法适用于含有表决模型的混联系统进行多任务剖面下的可靠性建模,对于逻辑结构变化导致组件数量不同的可靠性评估模型,可以根据工程实际分配表决模型中δ、α、β的数值;并获得系统综合可靠性评估结果。
2) 通过动态贝叶斯网络对组件故障状态的描述和分析,在多任务剖面条件下考虑待工作组件的不同故障状态对系统可靠性的影响,可以更详细地反映设备在多任务剖面条件下的综合可靠性评估情况,从而更具有实际意义。这种方法提高了混联系统可靠性计算的精度,也可以用于提前预知故障影响程度,及时更换故障组件,进而进一步提高电子系统的可靠性。
[1] THURLBECK A P,CAO Yue.A mission profile-based reliability modeling framework for fault-tolerant electric propulsion[J].IEEE Transactions on Industry Applications,2022,58(2):2312-2323.
[2] LU Yiping,XIANG Enyao,ZHU Lin,et al.Mission profile-based lifetime estimation and its system-controlled improvement method of IGBT modules for electric vehicle converters[J].CPSS Transactions on Power Electronics and Applications,2023.
[3] 史俊斌,于永利,韩雪魁,等.基于PMS的装备作战单元复杂任务可靠性研究[J].兵工自动化,2007(8):9-10.SHI Junbin,YU Yongli,HAN Xuekui,et al.Research on mission reliability of combat unit complex task based on PMS[J].Ordnance Industry Automation,2007(8):9-10.
[4] TAERIM RYU,UI-MIN CHOI,IONUT VERNICA,et al.Effect of thermal loading definitions on the mission profile-based reliability evaluation of power devices in PV inverters[J].Microelectronics Reliability,2022,138.
[5] LIN Kunsong,CHEN Yunxia.Two new multi-phase reliability growth models from the perspective of time between failures and their applications[J].Chinese Journal of Aeronautics,2021,34(5):341-349.
[6] 卞瑞兵,张扬,潘正强,等.基于二元决策图的护航编队多阶段任务体系可靠性分析[J].兵工学报,2020,41(5):1016-1024.BIAN Ruibing,ZHANG Yang,PAN Zhengqiang,et al.Reliability analysis of multi-phase mission system of escort formation based on binary decision diagram[J].Journal of Military Engineering,2020,41(5):1016-1024.
[7] MO Yuchang,XING Liudong,AMARI SUPRASAD V.A multiple-valued decision diagram based method for efficient eliability analysis of non-repairable phased-mission systems[J].IEEE Transactions on Reliability,2014,63(1):320-330.
[8] 杜海东,曹军海,刘福胜.基于Bayes网络的装备多阶段任务系统可靠性建模与评估研究[J].兵器装备工程学报,2021,42(6):170-174.DU Haidong,CAO Junhai,LIU Fusheng.Research on reliability modeling and evaluation of equipment multi phase mission system based on Bayes network[J].Journal of Ordnance Equipment Engineering,2021,42(6):170-174.
[9] CAI Baoping,LIUYonghong,ZHANG Yunwei,et al.Dynamic Bayesian networks based performance evaluation of subsea blowout preventers in presence of imperfect repair[J].Expert Systems with Applications,2013,40(18):7544-7554.
[10] WANG Chuan,LIU Yupeng,HOU Wen,et al.Reliability and availability modeling of subsea autonomous high integrity pressure protection system with partial stroke test by dynamic bayesian[J].Proceedings of the Institution of Mechanical Engineers,Part O:Journal of Risk and Reliability,2021,235(2):268-281.
[11] 谢红卫,宫二玲,贺勇军.时变结构多阶段任务系统的可靠度研究[J].国防科技大学学报,1999(5):44-48.XIE Hongwei,GONG Erling,HE Yongjun.Reliability study of time varying multi phase task system[J].Journal of National University of Defense Technology,1999(5):44-48.
[12] 范文亮,张永进.基于加权BDD的飞行器多阶段任务系统可靠性分析[J].机械研究与应用,2015,28(5):64-68.FAN Wenliang,ZHANG Yongjin.Reliability analysis of aircraft multi-stage mission systems based on weighted BDD[J].Mechanical Research &Application,2015,28(5):64-68.
[13] BENANZER TODD W.System design of undersea vehicles with multiple sources of uncertainty[D].USA:Wright State University,2008.
[14] 古莹奎,张全新,梁玲强,等.基于BDD考虑共因失效的多阶段任务系统可靠性分析方法[J].机械设计与研究,2017,33(2):1-5.GU Yingkui,ZHANG Quanxin,LIANG Lingqiang,et al.Reliability analysis method of phased-mission systems with common cause failure based on BDD[J].Machine Design &Research,2017,33(2):1-5.
[15] 刘震宇,马小兵,洪东跑,等.基于飞行剖面的作战飞机任务可靠性评估方法[J].北京航空航天大学学报,2012,38(1):59-63.LIU Zhenyu,MA Xiaobing,HONG Dongpao,et al.Operational aircraft mission reliability assessment method based on flight profile[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38 (1):59-63.
[16] 周思醒,杨建军,胡涛.舰船总体任务可靠性建模新方法[J].中国舰船研究,2010,5(1):52-55.ZHOU Sixing,YANG Jianjun,HU Tao.A new method to establish reliability model for overall mission of ships[J].chinese journal of ship research,2010,5 (1):52-55.
[17] 吕建伟,余鹏,刘中华,等.舰船总体任务可靠性的多阶段工程分析法[J].中国造船,2011,52(3):182-189.LYU Jianwei,YU Peng,LIU Zhonghua,et al.Phased engineering analysis approach of whole ship’s mission reliability[J].Shipbuilding of China,2011,52(3):182-189.
[18] 闫华,王魁,刘子林,等.基于Markov方法的多阶段任务系统可靠性分析综述[J].兵器装备工程学报,2016,37(6):92-96.YAN Hua,WANG Kui,LIU Zilin,et al.Overview of reliability analysis of multi-stage mission system based on Markov method[J].Journal of Ordnance Equipment Engineering,2016,37(6):92-96.
[19] WANG Lizhi,ZHAO Xuejiao,ZHANG Yuan,et al.Unmanned aerial vehicle swarm mission reliability modeling and evaluation method oriented to systematic and networked mission[J].Chinese Journal of Aeronautics,2021,34(2):466-478.
[20] 王刚,武小悦,卢立常.基于BDD的航天测控系统任务可靠性分析[J].飞行器测控学报,2011,30(2):20-24.WANG Gang,WU Xiaoyue,LU Lichang.BDD-based analysis of the mission reliability of TT&C systems[J].Journal of Spacecraft TT&C Technology,2011,30(2):20-24.