0 引言
欠驱动系统是指系统控制的输入数目小于系统自由度的一类非线性系统,由于欠驱动系统具有非线性、参数摄动、易受干扰、多目标等特点,又广泛应用于国防军事、航空航天、地质勘测等领域,至今仍是国内外控制领域学者关注的重点[1-4]。常见的欠驱动系统有:倒立摆系统[5]、球杆系统[6]等。对于欠驱动不稳定系统的控制方法主要有:线性二次型(LQR)最优控制[7]、比例积分微分(PID)控制[8]、自抗扰控制方法(ADRC)[9]等。
自抗扰控制(ADRC)是我国韩京清[10]提出的一种不依赖于被控过程模型的一种非线性控制方法,众多学者在自抗扰控制的研究中做了大量工作,实践证明了这是一种具备工程应用潜力的控制技术。广大学者针对自抗扰控制在欠驱动系统中的应用进行了改进,如:文献[11]中应用双ESO的形式对欠驱动倒立摆系统的小车位置和摆杆角度的扰动分别进行实时观测补偿,实现了对欠驱动倒立摆系统的较好控制,然而该方法可调参数较多,调参步骤较为繁琐;文献[12]中通过分析和实验证明了自抗扰控制对倒立摆系统控制的优势;文献[13]中正对自抗扰控制器参数难以整定的问题,提出一种带宽参数化的线性自抗扰控制方法,进行控制器参数寻优。然而基于传统fal函数设计ESO观测效果较差,控制精度不够高。
本研究中提出了一种欠驱动变结构自抗扰控制方法。首先,针对传统非线性函数在原点处的光滑度不够问题,设计了一种新型非线性qal函数,基于该非线性函数设计了改进型扩张状态观测器(ESO),用于观测倒立摆系统的摆杆角度的扰动误差。设计了2个线性跟踪微分器分别对小车的实时位移和速度及其控制量进行观测分析,改变了传统ADRC控制策略中只采用一个跟踪微分器(TD)的方式,突破了传统ADRC只适用于单输入单输出的问题。同时用线性控制率替换非线性状态误差反馈控制率,用以实现对摆杆偏角和小车位移的实时控制。最后,将驱动变结构自抗扰控制方法与传统自抗扰控制进行了系统对比和实验研究。
1 欠驱动直线一级倒立摆数学模型
对欠驱动直线一级倒立摆系统作如下假设:① 小车和摆杆均为刚体;② 忽略空气流动阻力和摆杆与小车轴承之间的摩擦力。因此可将一级直线倒立摆系统定义成一个由匀质杆和小车组成的欠驱动系统,图1为模型示意图。
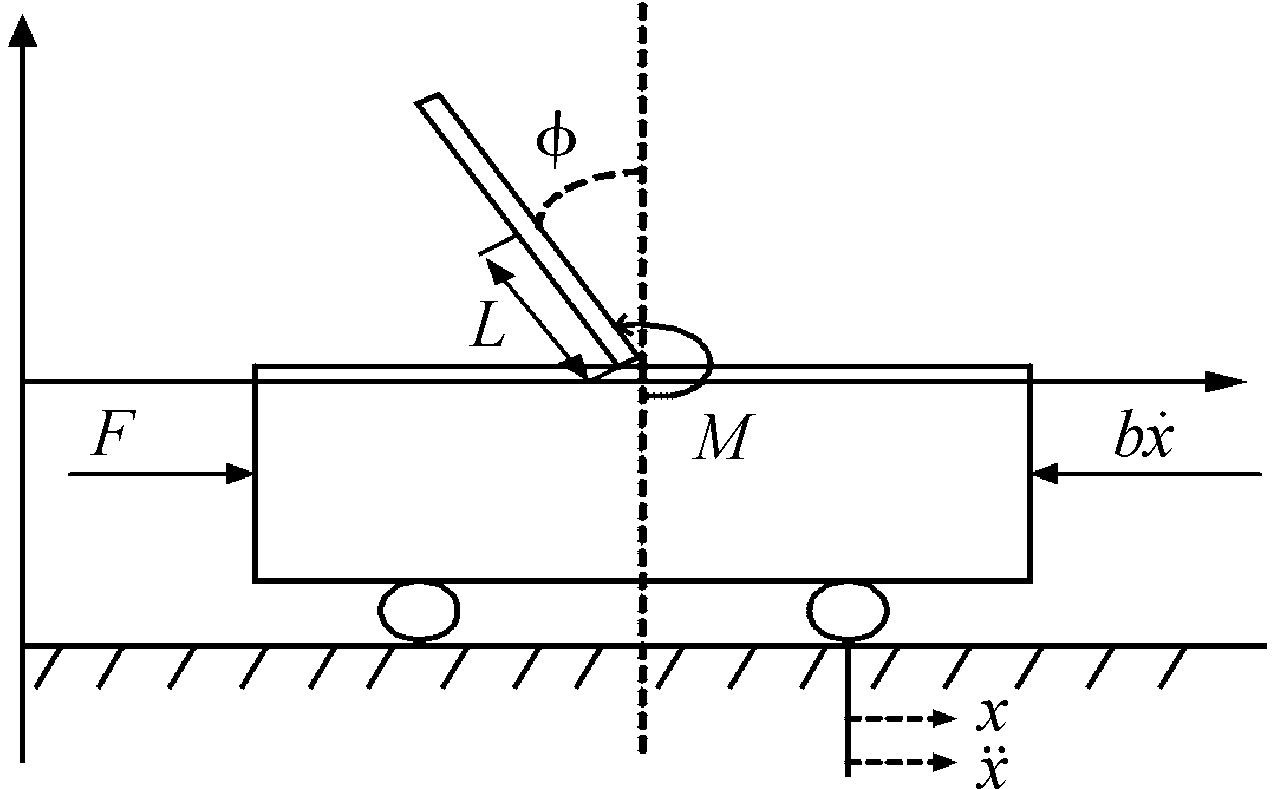
图1 欠驱动直线一级倒立摆数学模型
Fig.1 Mathematical model of an underactuated linear inverted pendulum
图1中,M为小车的质量,F为小车水平方向的受力, x为小车的移动距离,φ 为摆杆和垂直向上方向的夹角,![]() 为小车水平移动速度, b为小车速度的阻尼系数。
为小车水平移动速度, b为小车速度的阻尼系数。
分别在小车水平方向,摆杆的水平及竖直方向运用牛顿第二定律进行直线一级倒立摆的数学模型进行受力分析,用u来代表被控对象的输入F,线性化后最终得到下面2个运动方程:
![]()
(1)
在式(1)中对![]() 和
和![]() 进行求解代数方程,可得到如下解:
进行求解代数方程,可得到如下解:
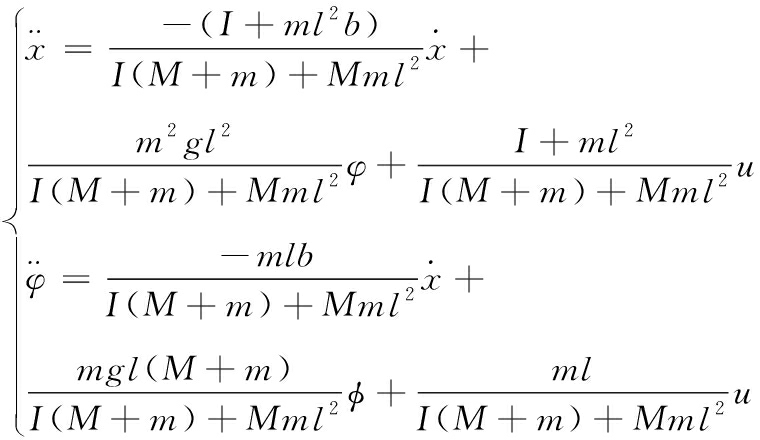
(2)
为了进一步得到系统的状态空间方程,选取小车的位移x,小车的速度![]() 摆杆的偏角φ,摆杆的角速度
摆杆的偏角φ,摆杆的角速度![]() 作为状态变量,整理得到状态空间方程为
作为状态变量,整理得到状态空间方程为
![]()
(3)

(4)
式(4)中:M为摆杆质量;g为重力加速度;l为一端到质心的长度;I为摆杆的转动惯量。
2 欠驱动系统自抗扰控制器设计
欠驱动一级直线倒立摆系统为单输入双输出系统,而传统的自抗扰控制仅适用于单输入单输出的系统,因此增加了一个跟踪微分器(TD),由2个TD来同时获取给定的位移和速度以及小车实时的位移和速度信号。控制率设计以摆杆偏角为主,用以实现小车位移和摆杆角度实时稳定控制的目的。设计的基于ADRC控制的欠驱动一级直线倒立摆控制系统结构如图2所示。图2中,v0为小车的位移,V0是输入给定的参考位移。
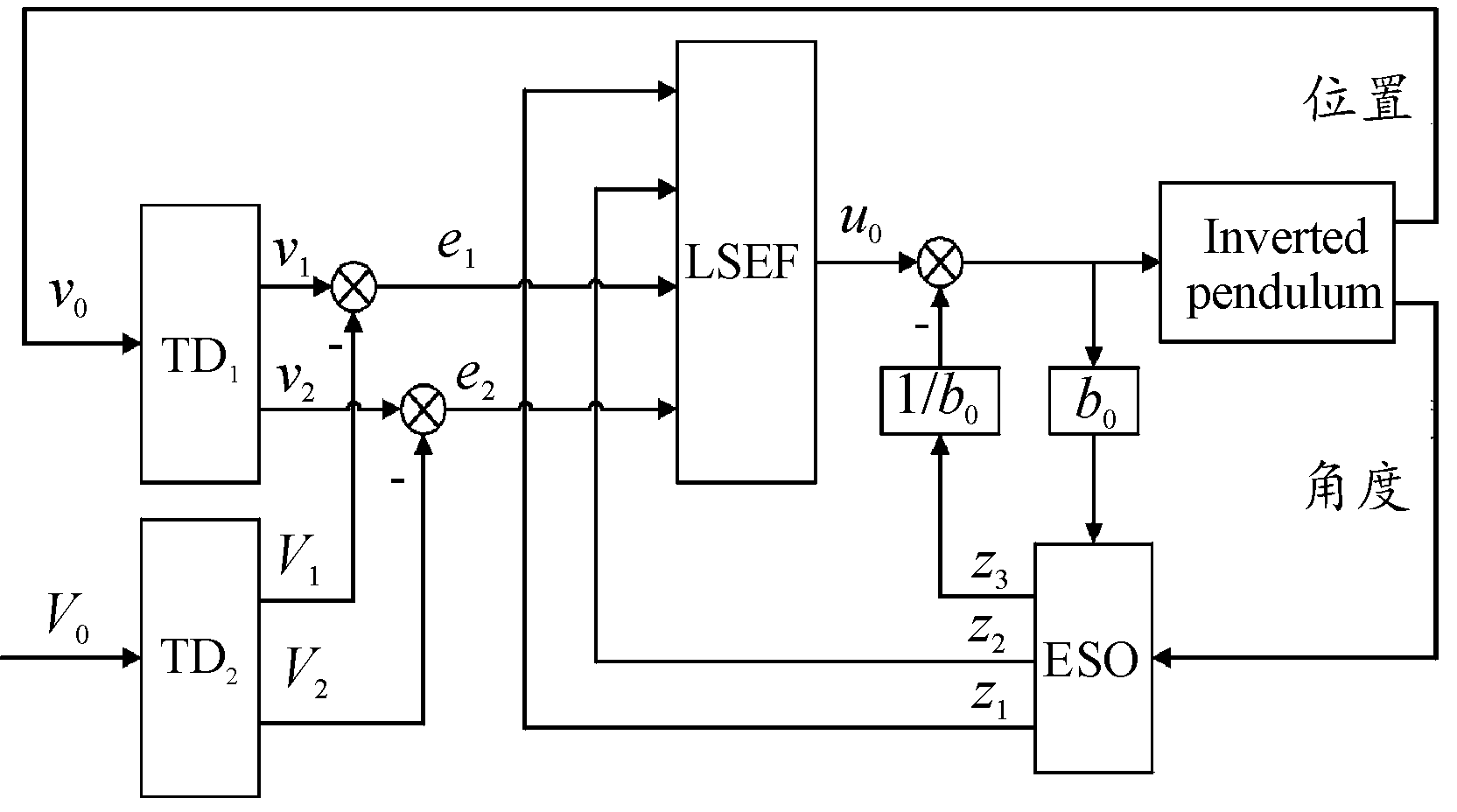
图2 欠驱动系统自抗扰控制器控制框图
Fig.2 Control block diagram of the active disturbance rejection controller of the underdrive system
2.1 改进型非线性函数的设计
非线性函数的选取直接关系到整个控制器的观测性能,通常非线性函数选取的原则为:函数关于原点对称且处处可导,其曲线有良好的连续性、收敛性、平滑性,待整定参数尽可能少,且需要遵循“小误差、大增益,大误差,小增益”的原则[14]。传统的非线性函数为
![]()
(5)
传统的非线性函数连续性平滑性效果不佳,并且在原点领域容易产生抖振,针对上述问题,设计一个连续光滑的非线性函数qal函数,从而提高控制器的性能。
当δ<|e|≤γ时,qal函数可表示为
qal(e,α,δ,γ)=![]() sign(e)
sign(e)
(6)
当|e|≤δ时,qal函数为三角函数与多项式拟合的形式,可表示为
qal(e,α,δ,γ)=l1e+l2sin2e+l3arctane
(7)
选用三角函数与多项式拟合而非纯指数函数多项式拟合一个重要原因是arctane比指数函数在原点附近的平滑性更好,并且这样的插值拟合方式保证了函数在原点处连续且可导的条件。在拟合过程需要满足2个条件:① 分段函数在定义域内连续;② 在分段点处可导,则成立式(8)
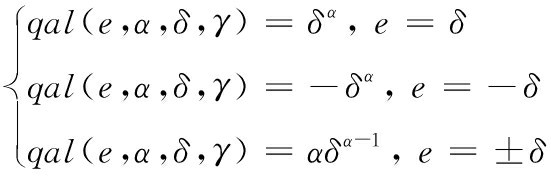
(8)
求解可得
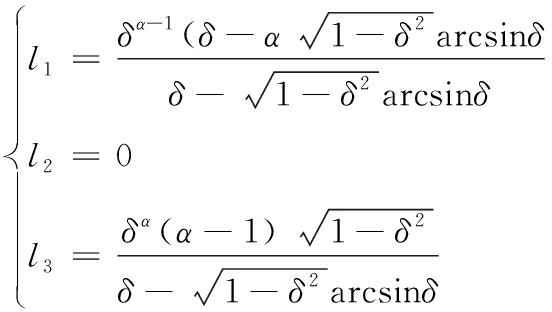
(9)
当|e|>γ时,误差较大,为了进一步提升系统的抗干扰能力,更好地遵循“大误差小增益,小误差大增益”的原则, 则qal函数的表达式为
qal(e,α,δ,γ)=γαsign(e)
(10)
最终得到完整的qal函数式为
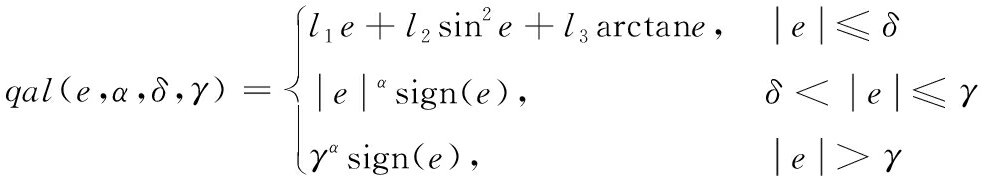
(11)
在Matlab仿真软件中取α=0.2、δ=0.25、γ=0.1,将非线性qal函数与传统非线性fal函数的输出曲线进行对比。qal函数与fal函数的特性曲线如图3所示,误差反馈增益对比如图4所示。

图3 函数仿真曲线对比
Fig.3 Comparison of function simulation curves
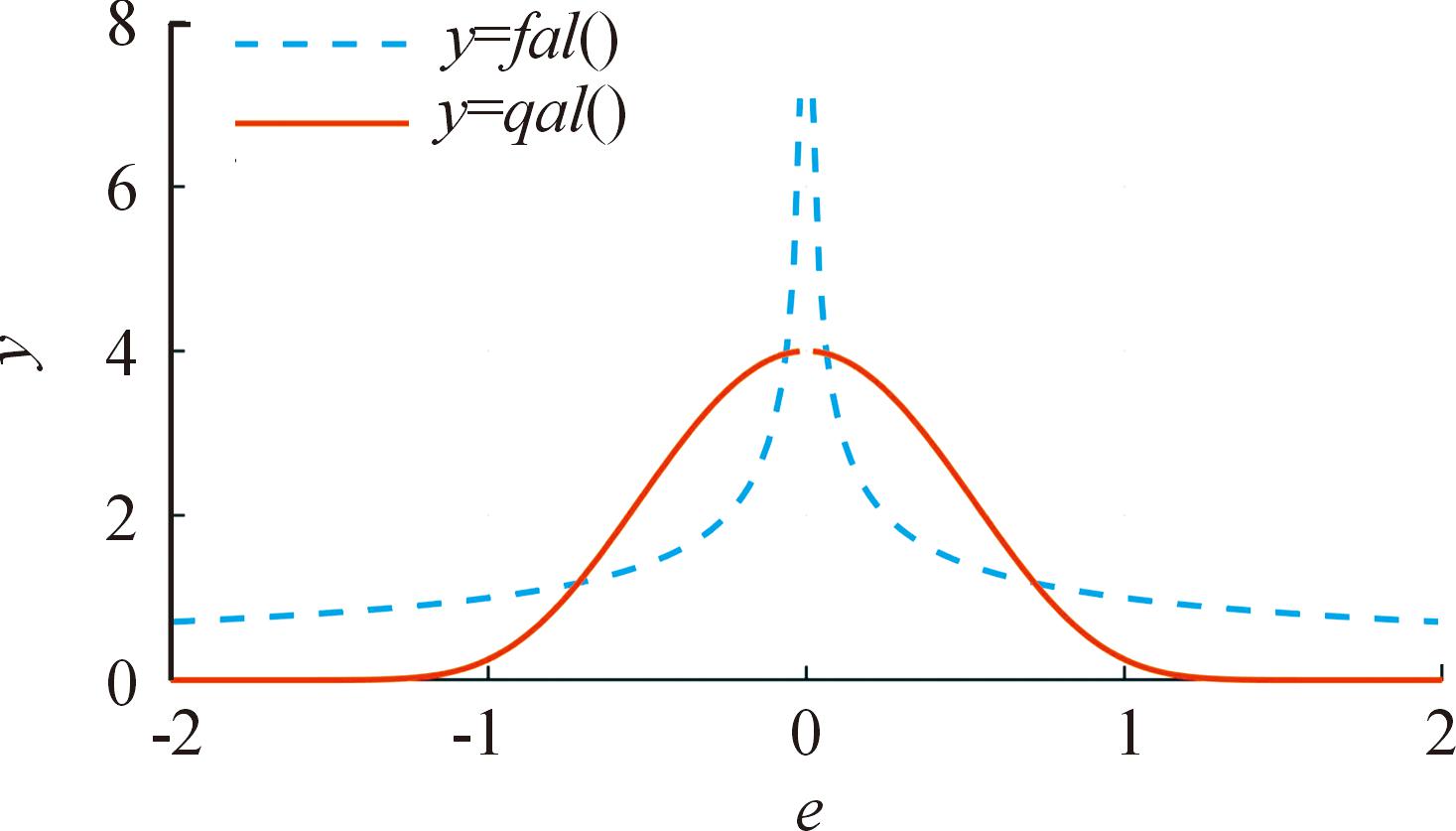
图4 函数误差增益对比曲线
Fig.4 Function error gain comparison diagram
由图3可以看出在误差大于1的时候,qal函数的输出量明显小于fal函数的输出值,并且在原点附近具有更好的收敛性和平滑性,克服了传统非线性函数在原点附近存在拐点的问题。
从图4可以看出,输入误差越小时qal函数和fal函数的误差增益均增大,输入误差较大时,2个函数误差增益均减小,2个函数都体现了选取非线性函数的“小误差大增益,大误差小增益”的必要原则。在图3中可以明显看到在原点处qal函数的曲线平滑性比fal的更好,因此qal函数输出增益在误差较小时不易引起系统振荡,使基于qal函数设计的改进型ESO具备更好的观测能力,并且能够更好地缩小跟踪系统状态时产生的偏移量,从而提高了系统的控制精度和抗干扰能力。
2.2 跟踪微分器设计
为了得到小车的实际位移的跟踪值和微分值,同时可以对其有一定的滤波功能,将传统的非线性TD改为线性TD形式,一方面减少了采用非线性函数的计算量,另一方面更利于现实控制的实现,为此设计TD1,形式为
![]()
(12)
式(12)中:v0为小车的实际位移;v1为v0的安排过渡过程即小车位移的跟踪值;v2为近似v1的微分即小车速度估计值;r1为可调参数。为了得到小车参考位移的跟踪值V1和微分值V2,再设计一个与TD1形式相同的跟踪微分器TD2,可调参数记为r2。
线性跟踪微分器能够避免非线性组合幂次函数fal中的符号函数带来的高频抖振现象和引入噪声放大的问题。跟踪微分器的输出曲线如图5和图6所示。
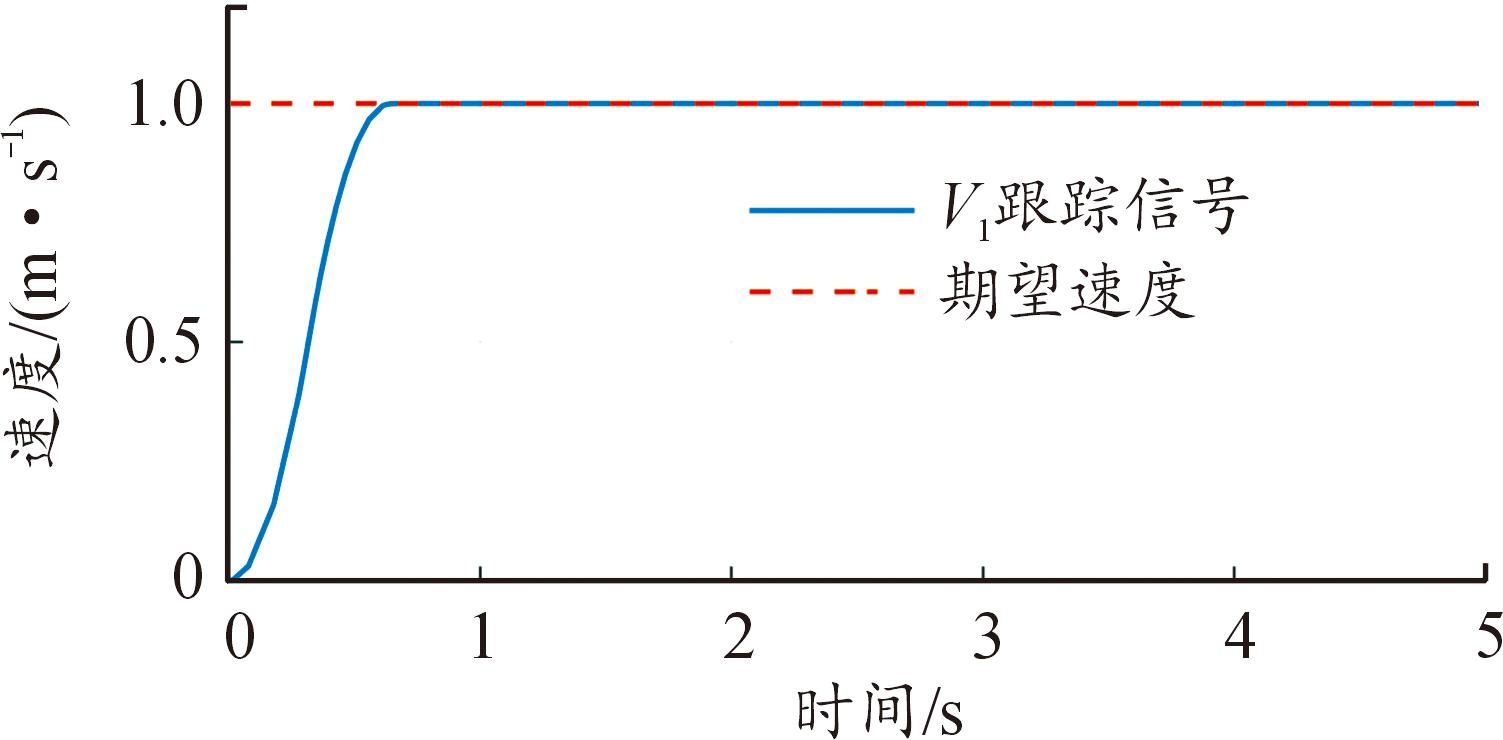
图5 跟踪微分器V1输出响应曲线
Fig.5 Trace differentiator V1 output response curve

图6 跟踪微分器V2输出响应曲线
Fig.6 Trace differentiator V2 output response curve
从图5和图6中可以看出设计的线性跟踪微分器具有良好的响应速度和滤波功能,并且微分信号无噪声。
2.3 扩张状态观测器设计
ESO是自抗扰控制器中的核心与关键所在,结合所设计的光滑性更好的改进型qal非线性函数,能够更好地得到摆杆偏角的跟踪值z1,摆杆偏角的微分值z2,以及综合扰动z3,其对摆杆偏角设计的改进型ESO形式为
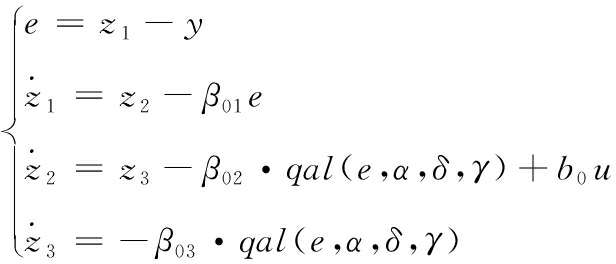
(13)
式(13)中:e为观测误差;b0为补偿因子;u为控制输出; β01、β02、β03为改进型ESO的增益;σ1、σ2为非线性因子。将式(13)中的β01、β02、β03采用文献[15]中的带宽法使其配置成![]() 形式,可将式(13)改写为
形式,可将式(13)改写为
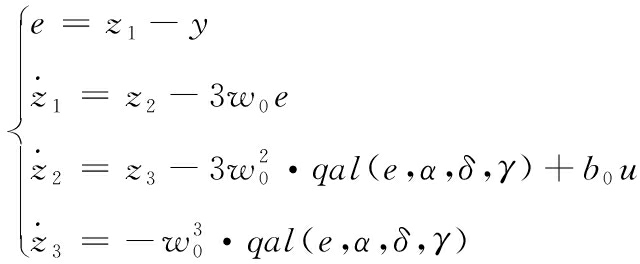
(14)
令e1=z1-x1、e2=z2-x2、e3=z3-x3,则整个系统的误差方程可以重构为
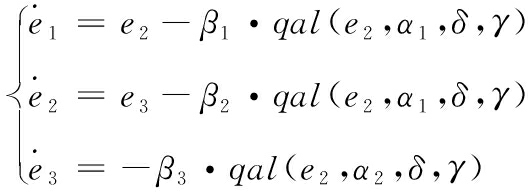
(15)
式(15)可以写成
![]()
(16)
其中:

(17)
根据引理:若存在矩阵
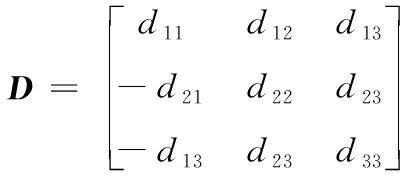
(18)
并且矩阵的主对角元素都是正数,使得D·A(e)满足正定矩阵,则误差方程的零解是渐进稳定的。根据式(14)的研究结论可得出:β1β2-β3>0 时,存在矩阵D,使得DA(e)是正定矩阵,误差方程的零解渐近稳定。
2.4 线性误差反馈控制率设计
控制率部分采用的是线性化方法,将传统的非线性控制率由2个非线性函数乘以各自的增益累加之后输出的形式,改成采用2个PD控制组合的形式如式(19)所示,因此需要调节的参数只有k1、k2、k3、k4 4个。
![]()
(19)
式(19)中,k1、k2、k3、k4为控制器的增益,符号以构成负反馈为准[16]。
3 仿真与实验分析
3.1 欠驱动直线一级倒立摆仿真实验对比
在Matlab/Simulink中对欠驱动直线一级倒立摆进行仿真实验,倒立摆所采取的实际参数如表1所示。
表1 欠驱动倒立摆实际参数
Table 1 Actual parameters of underactuated inverted pendulum

变量名实际参数名实际参数值M/kg小车质量1.095m/kg摆杆质量0.105b/(N·s·sec-1)小车速度阻尼系数0.1l/m摆杆转动轴到摆杆中心的长度0.3I/(kg·m2)摆杆转动惯量0.003 15G/(m·s-2)重力加速度9.8L/m电机导轨长度0.5
自抗扰控制器采取r1=40,r2=15,b0=-1.8,w0=60,k1=750,k2=220,k3=3,k4=140各参数值,采样周期取0.005 s,根据系统的响应快慢需求预先可以调试到r1和r2的值来决定系统跟踪目标的速度;b0为系统控制输入的放大系数。
为了验证变结构自抗扰控制的控制性能,将变结构自抗扰控制方法与传统ADRC和文献[13]中基于差分进化算法的自抗扰控制方法(以下简称差分算法ADRC)进行摆杆角度控制仿真对比,结果如图7所示。
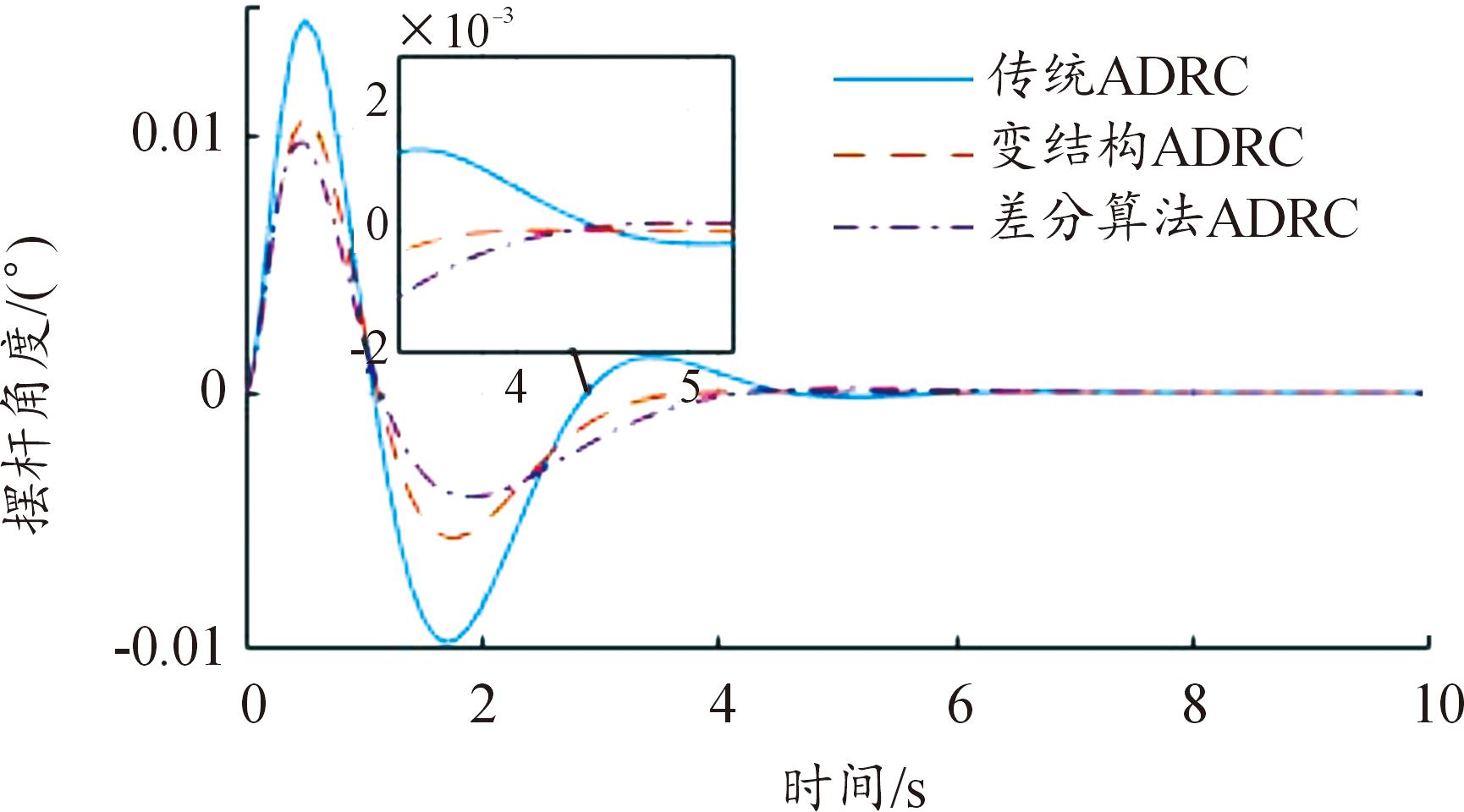
图7 摆杆角度控制曲线
Fig.7 Swing rod angle control curve
进一步将摆杆的偏角仿真结果绘制成图表进行实验分析,通过峰值数据和响应时间能够更加直观地得出对比结论,见表2所示。
表2 摆杆偏角控制对比
Table 2 Comparison of swing angle control
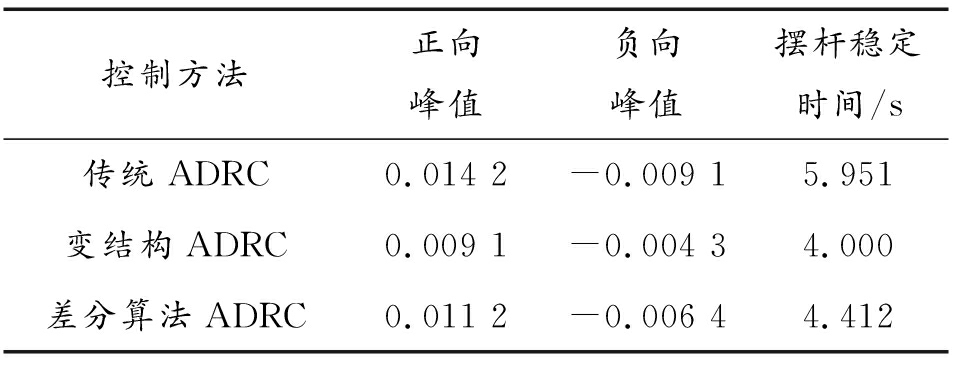
控制方法正向峰值负向峰值摆杆稳定时间/s传统ADRC0.014 2-0.009 15.951变结构ADRC0.009 1-0.004 34.000差分算法ADRC0.011 2-0.006 44.412
表2可以看出,起摆时变结构ADRC的正向峰值为0.009 1,差分算法ADRC和传统ADRC的正向峰值分别为0.011 2和0.014 2;变结构ADRC的负向峰值为-0.004 3,差分算法ADRC和传统ADRC的负向峰值分别为-0.006 4和-0.009 1。因此变机构ADRC的正负向峰值为三者中最小,起摆更稳定。从摆杆稳定时间来看,变结构ADRC在4.000 s时候摆杆达到稳定,差分算法ADRC和传统ADRC摆杆稳定时间分别为4.412 s和5.951 s,变结构ADRC最先达到稳定。通过仿真验证了变结构ADRC控制方法在摆杆偏角控制的速度和稳定性上的优势。
3.2 欠驱动系统驱动电机的实验比较
为了进一步分析基于欠驱动倒立摆改进型ADRC的控制性能。以倒立摆驱动电机为实验对象,设计了3个实验进行验证分析,系统采用的驱动电机参数如表3所示。
表3 驱动电机实际参数
Table 3 Actual parameters of the drive motor

序号参数名称数值1额定转速/(r·min-1)3 0002额定功率/W4003额定电流/A2.54额定转矩/(N·m)1.275额定电压/V2006最高转速/(r·min-1)6 000
实验1:变结构自抗扰控制方法中,较传统ADRC控制方法采用了2处改进:① 采用双TD分别对实际位移和参考位移实时跟踪;② 将传统非线性函数进行改进引入到ESO中。为了分别验证2种改进方法分别对系统性能的影响,以倒立摆驱动电机的位置控制为实验对象,采用3组实验进行验证,得出电机位置控制曲线如图8—图10所示。
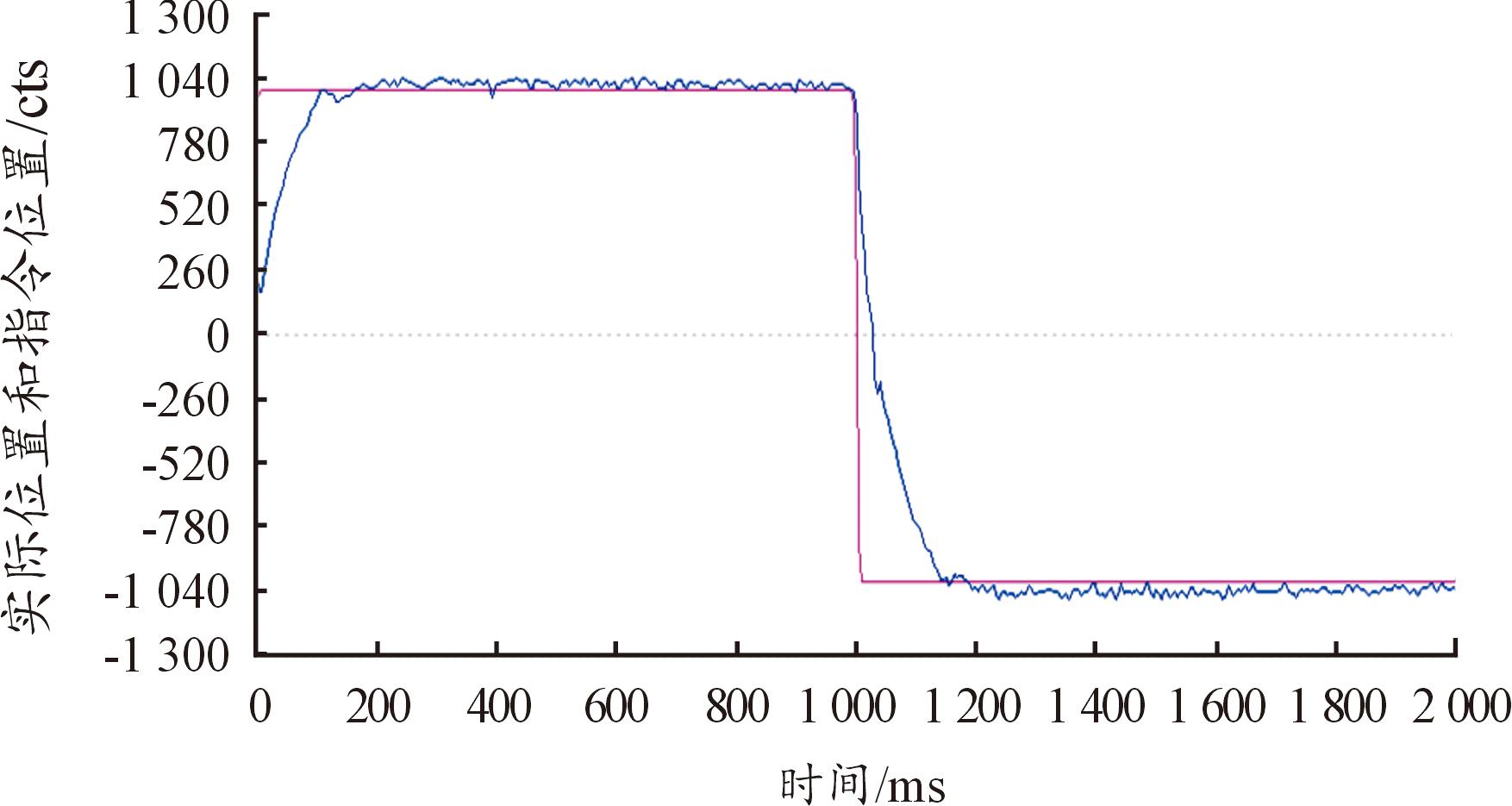
图8 仅采用双TD的ADRC
Fig.8 ADRC with only two TDS
图8为采用TD1和TD2分别对电机位置实时信号和参考信号进行的跟踪,同时ADRC控制器采用传统非线性函数的ESO,得到的位置控制曲线;图9为采用一个TD仅对电机的实时位置信号进行跟踪,同时采用改进型qal函数设计的ESO,对电机的实时位置信号进行观测,得到的位置控制曲线;图10为采用TD1和TD2分别对电机位置实时信号和参考信号进行跟踪,同时也采用改进型qal函数设计的ESO对实时位置信号观测,得到的电机位置曲线。
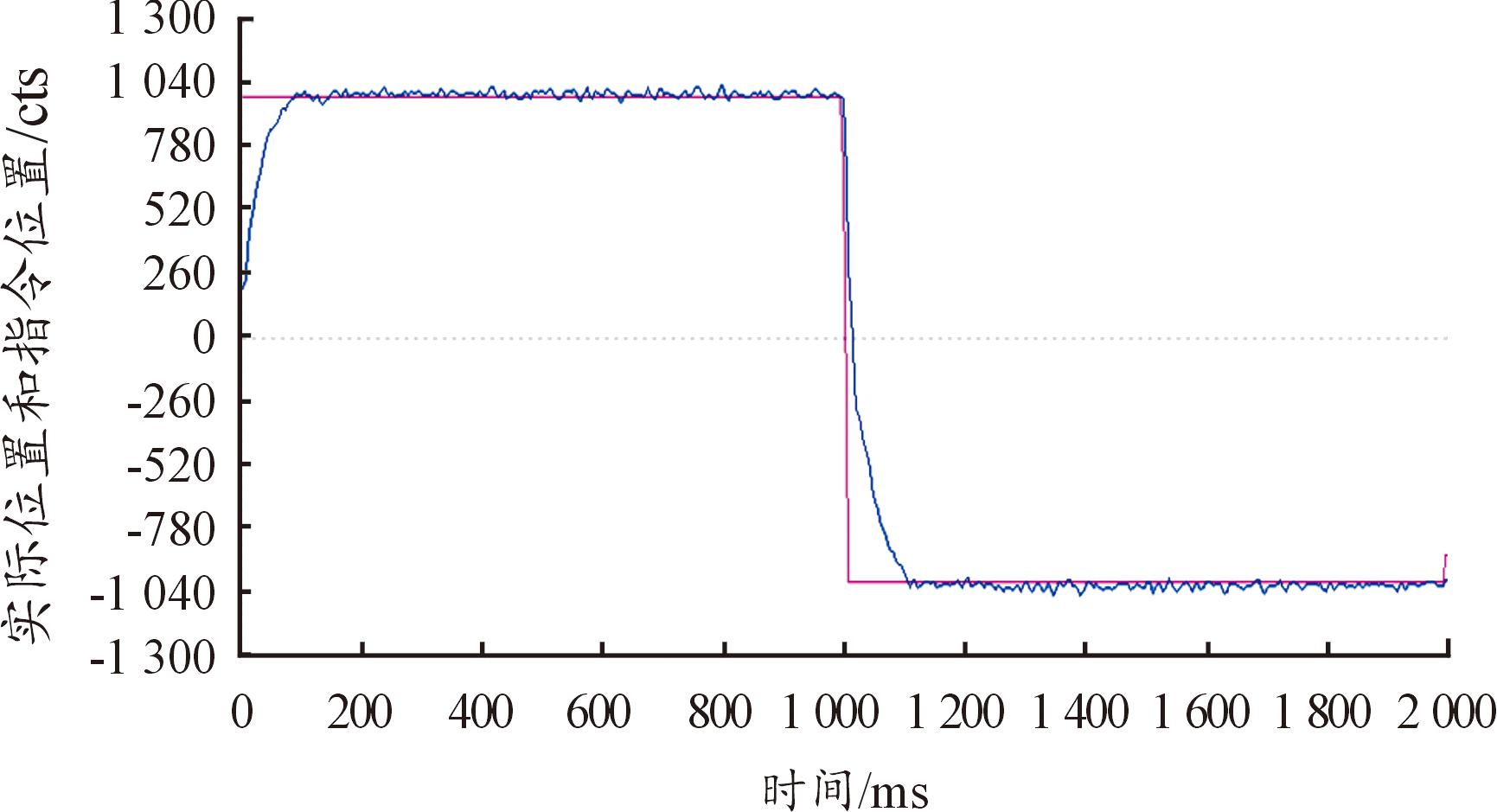
图9 仅采用改进型ESO
Fig.9 ADRC with only the modified ESO
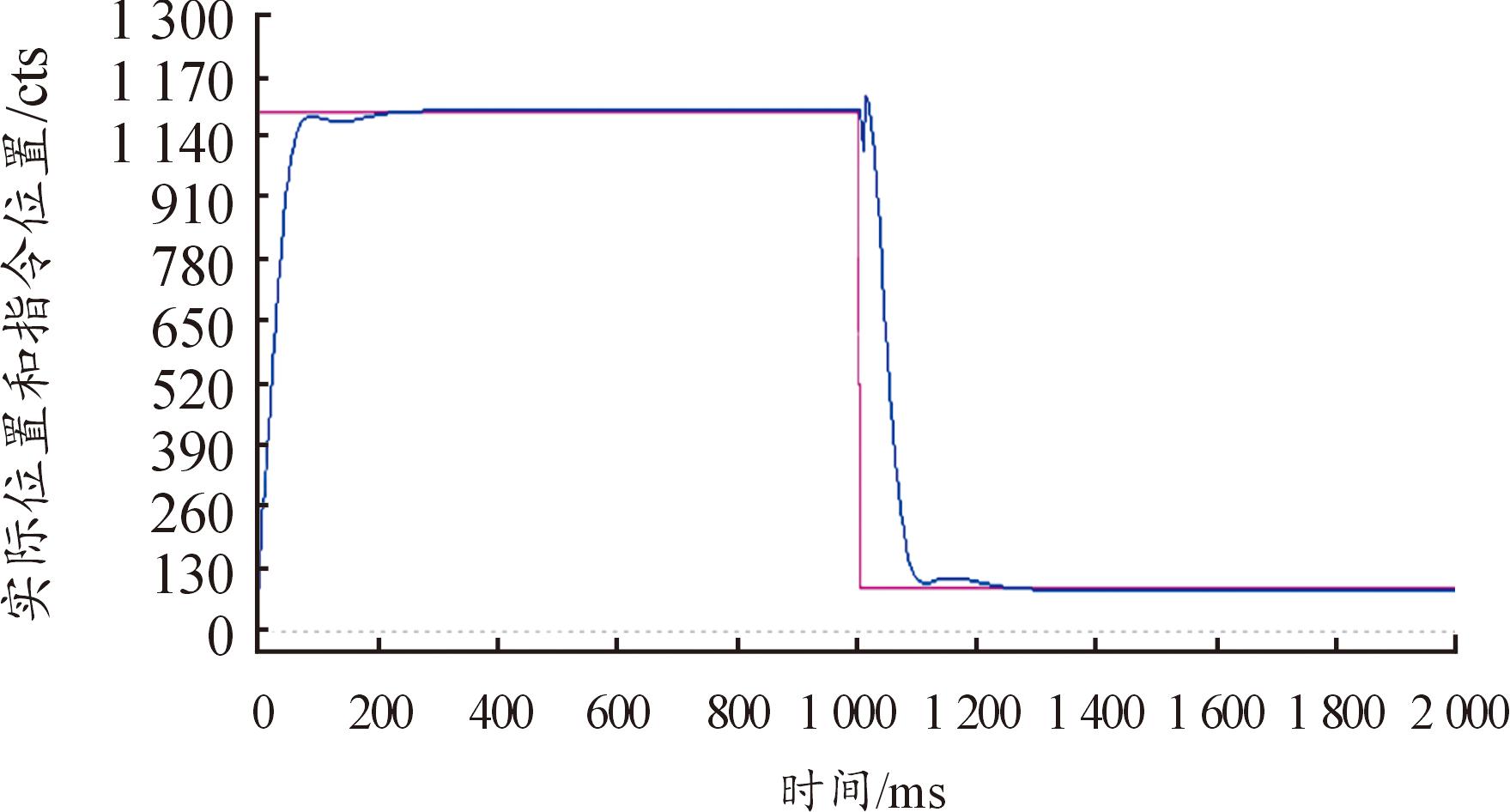
图10 同时使用双TD和改进型ESO的ADRC
Fig.10 ADRC using both dual TDS and an improved ESO
通过3个实验的电机位置控制对比图可以看出,同时采用2种改进方法的变结构ADRC的位置跟踪曲线稳定跟踪后更为平稳,切跟踪速度较快,跟踪精度更高。进一步证明了双TD对参考位置信号和实际位置信号跟踪的有效性,同时验证了改进型ESO对系统信号的观测和安排过渡对系统的控制性能的有效提升。
实验2:为了验证设计的2个跟踪微分器对信号的跟踪作用同时有效,同样以倒立摆驱动电机的位置控制为实验对象,进行了3组实验:① 仅采用TD1跟踪实际位置;② 仅采用TD2跟踪参考位置;③ 同时采用TD1和TD2分别对实际位置和参考位置进行跟踪。以正弦信号作为参考信号,得出3组实验的电机位置跟踪曲线分别如图11—图13所示。
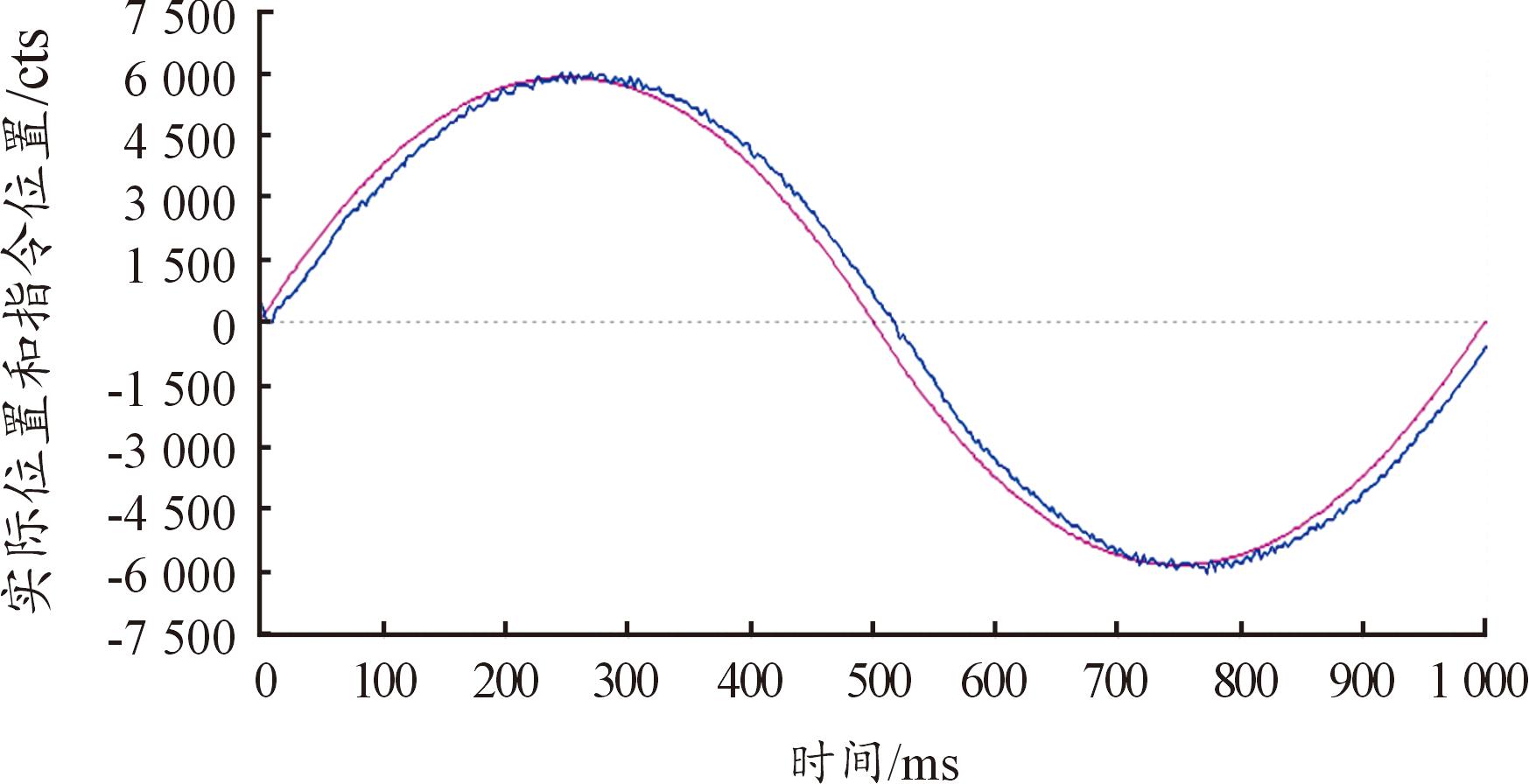
图11 仅采用TD1的电机位置跟踪曲线
Fig.11 Motor position tracking curve using only TD1
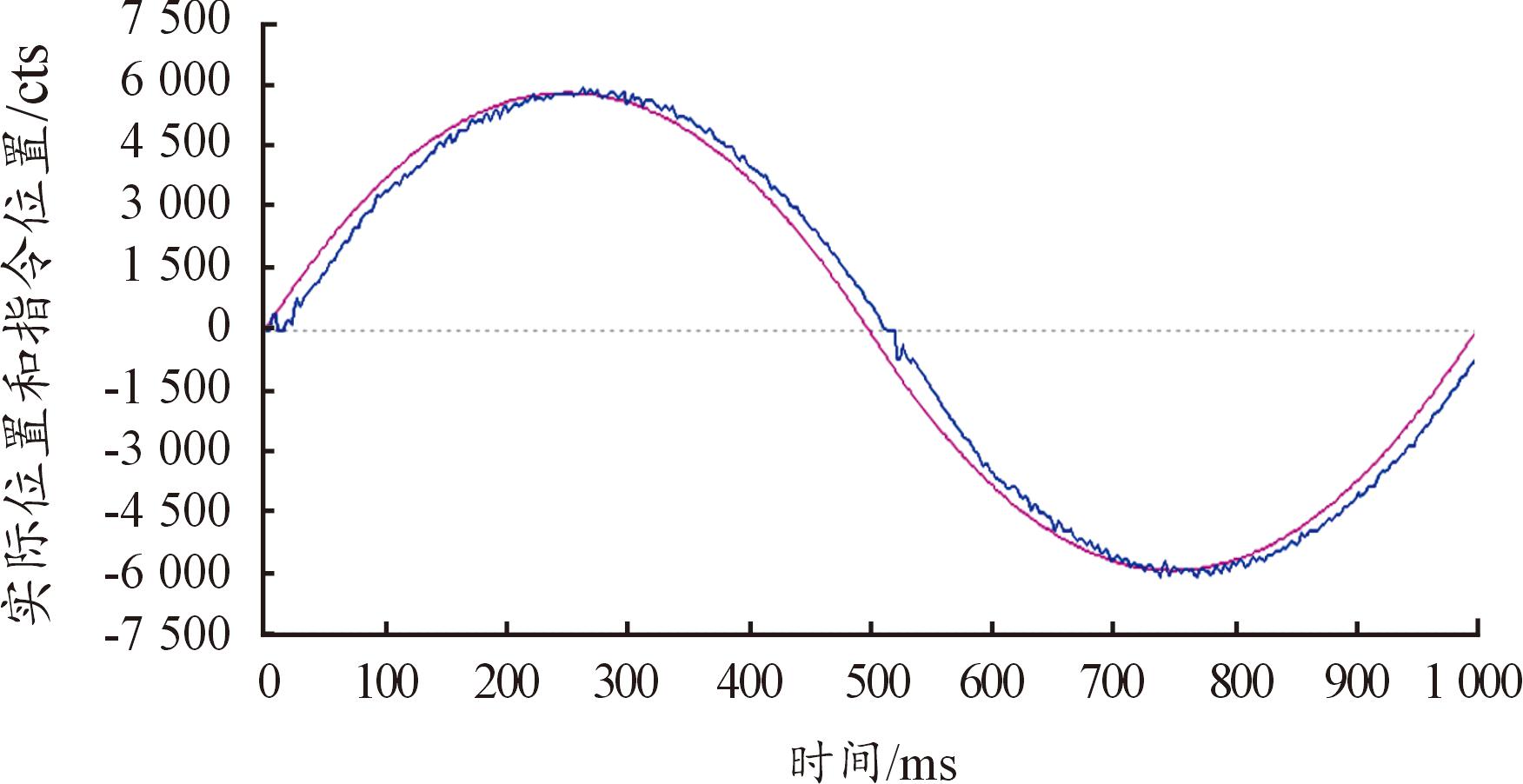
图12 仅采用TD2的电机位置跟踪曲线
Fig.12 Motor position tracking curve using only TD2
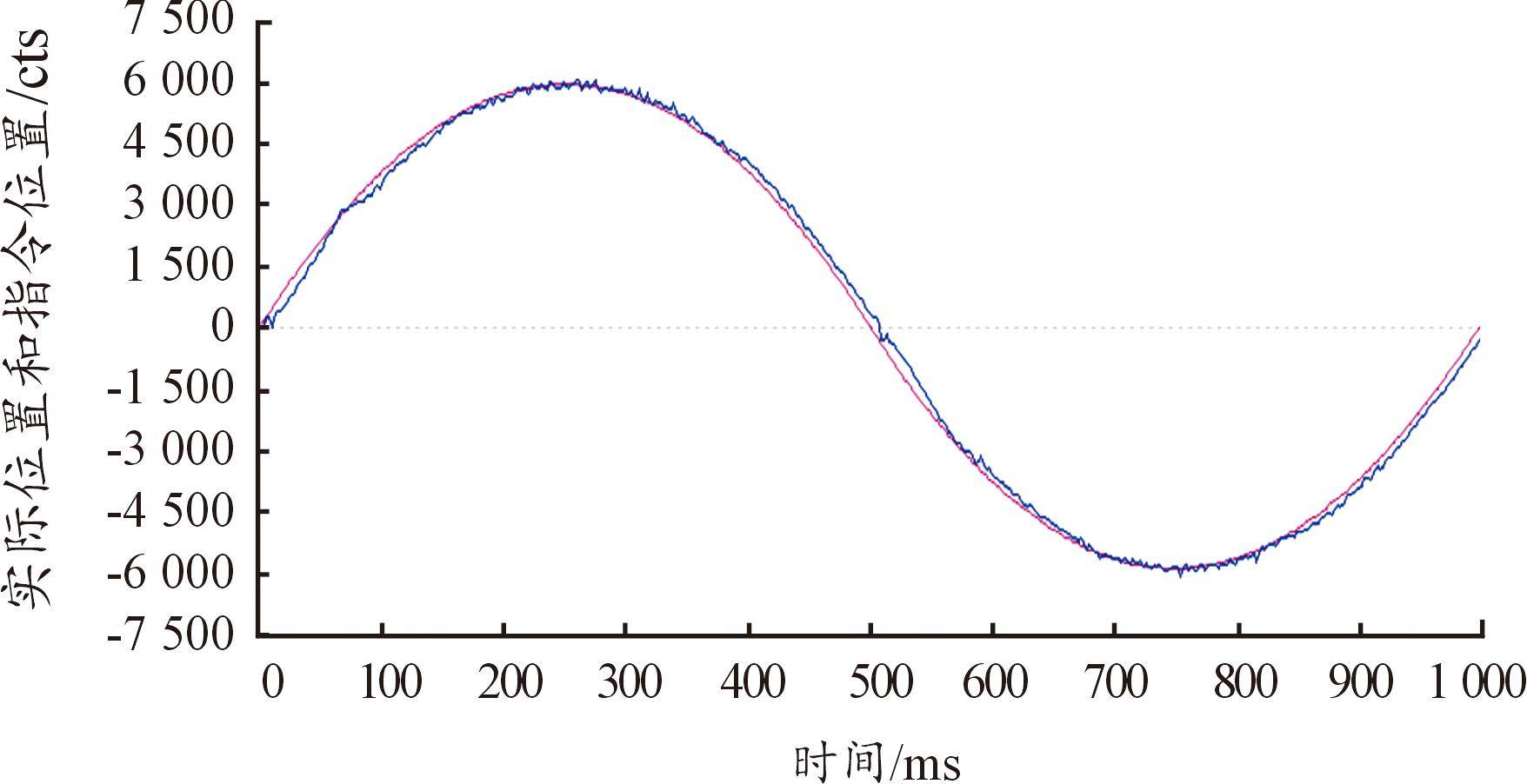
图13 同时采用TD1和TD2的电机位置跟踪曲线
Fig.13 Motor position tracking curve using both TD1 and TD2
从3个实验的对比图可以明显看出同时采用TD1和TD2的电机位置跟踪曲线跟踪效果较好,控制精度更高,从而验证了TD1对实际位置信号的跟踪和TD2对参考位置信号的跟踪同时对倒立摆控制系统的控制性能提升上起到了较好的作用。
为了验证改进型ADRC的抗干扰能力,同样以倒立摆驱动电机的位置控制作为实验对象,输入阶跃信号运行5 s后加入40 rad脉冲信号,比较抗干扰性能的程度。如图14所示。

图14 抗干扰响应曲线
Fig.14 Anti-interference response curve
从图14可以看出,对于直线一级倒立摆的驱动电机位置控制,变结构ADRC相对于传统的ADRC及差分算法ADRC具备更小的超调量、更快的跟踪速度和更低干扰脉冲的优势。结果表明,改进后的自抗扰控制器具有较好的响应速度和鲁棒性。
3.3 欠驱动直线一级倒立摆平台实验
在验证了设计的自抗扰控制器对欠驱动直线一级倒立摆系统具有良好的理论控制之后,进一步在欠驱动直线一级倒立摆平台上验证改进型自抗扰控制方法的可行性,实验平台如图15所示,实验参数选取表1中的参数。

图15 欠驱动直线一级倒立摆实验平台
Fig.15 Underactuated linear one-stage inverted pendulum experiment platform
根据系统模型设计了变结构自抗扰控制算法,并进行了仿真验证。然后在Matlab/Simulink上构建控制算法,硬件接口采用C2000DSP模块。在实验平台上将改进型ADRC控制和传统ADRC控制进行对比。图16为摆杆稳定后的摆杆角度曲线,图17摆杆角度稳定后电机控制量对比曲线。

图16 摆杆角度控制曲线
Fig.16 Swing rod angle control curve
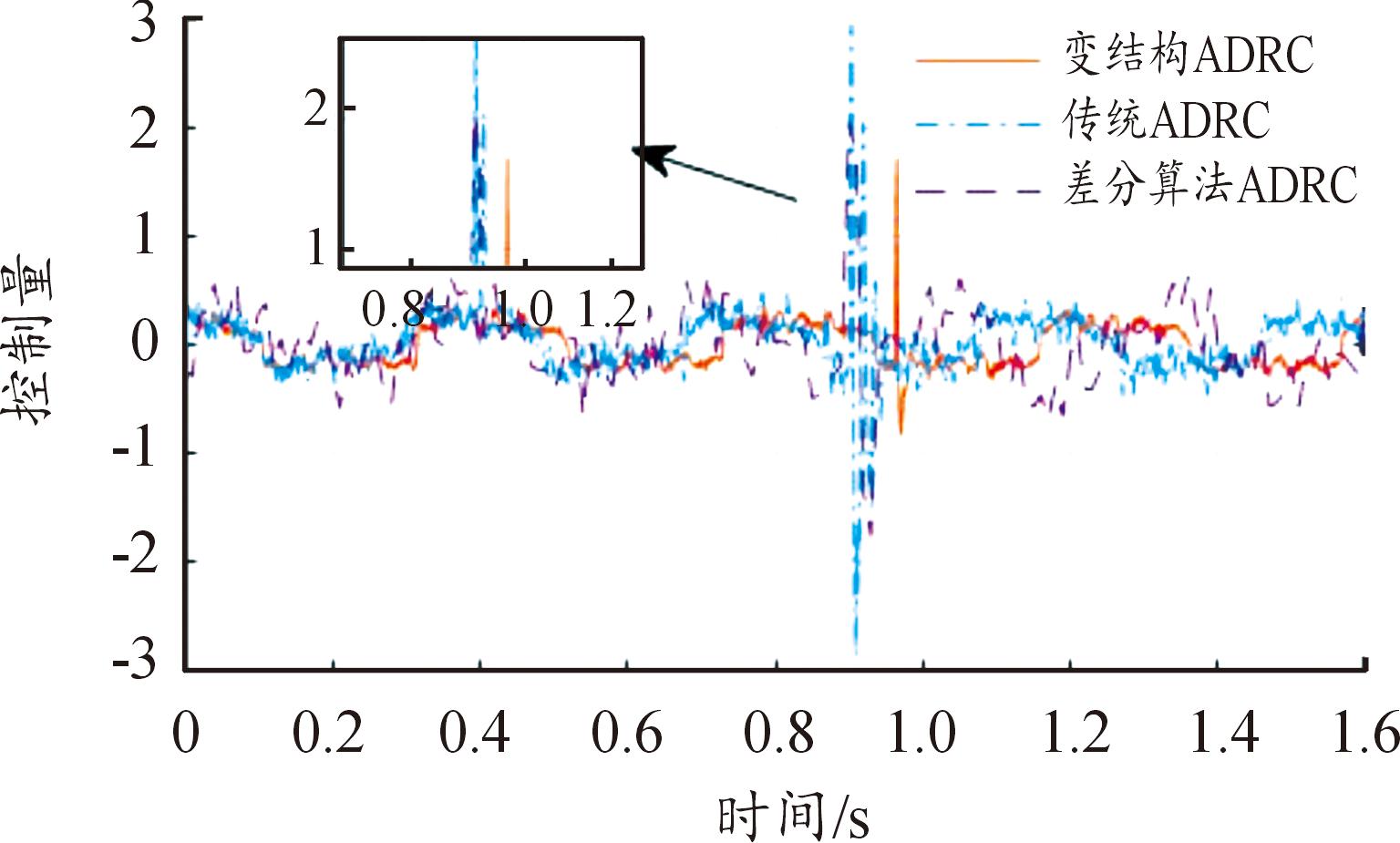
图17 控制量响应曲线
Fig.17 Response curve of control quantity
从图16可以看到变结构ADRC相比于传统ADRC和差分算法ADRC,可实现对摆杆角度的稳定控制,响应时间更短,响应幅度更小。从图17中可以看出改进型自抗扰控制策略的控制量相比于传统ADRC和差分算法ADRC更小。变结构自抗扰控制方法中采用2个TD同时对实际和参考信号同时跟踪,同时采用观测性更好的改进型ESO对系统控制量观测和补偿,提升了系统的控制性能。
4 结论
1) 设计的qal函数比传统fal函数在原点处平滑性更好,且更好地满足了 “小误差、大增益,大误差,小增益”的原则。应用qal函数的ESO比传统ESO具备更好的观测能力。
2) 通过Matlab仿真和实验将变结构ADRC与传统ADRC和差分算法ADRC对比,证明了变结构自抗扰控制方法较传统自抗扰控制具备较好的控制精度和抗扰动能力。
3) 所设计的改进型自抗扰控制器在很大程度上解决了对于欠驱动倒立摆这类系统难以实现单输入多输出同时有效控制的问题,具有一定的研究意义。
[1] 王杰,强宝民,何祯鑫,等.欠驱动双摆吊车滑模控制研究[J].兵器装备工程学报,2019,40(12):193-198,220.WANG Jie,QIANG Baomin,HE Zhenxin,et al.Research on sliding mode control of underactuated double pendulum crane system[J].Journal of Ordnance Equipment Engineering,2019,40(12):193-198,220.
[2] BROGLIATO B.Modeling analysis and control of robot-object nonsmooth underactuated Lagrangian systems:A tutorial overview and perspectives[J].Annual Reviews in Control,2023,55:297-337.
[3] JIANGAND J J,ASTOLFI A.Stabilization of a class of underactuated nonlinear systems via underactuated back-stepping[J].IEEE Transactions on Automatic Control,2021,66(11):5429-5435.
[4] 王丽琴.基于半实物仿真平台的倒立摆系统PID控制研究[J].船电技术,2022,42(5):22-24,28.WANG Liqin.Research on PID control of inverted pendulum system based on hardware in loop simulation platform[J].Marine Electric &Electronic Engineering,2022,42(5):22-24,28.
[5] 李俊芳,毕旺琪,李毅,等.ADRC-GPC算法在旋转倒立摆系统中的应用[J].传感器与微系统,2023,42(9):165-168.LI Junfang,BI Wangqi,LI Yi,et al.Applocation of ADRC-GPC algorithm for rotary inverted pendulum system[J].Transducer and Microsystem Technologies,2023,42(9):165-168.
[6] 马智慧,苏晓明,李桂君,等.改进的HDP算法研究及其在非线性系统中的应用[J].控制工程,2021,28(9):1893-1901.MA Zhihui,SU Xiaoming,LI Guijun,et al.Research on improved HDP algorithms and its application in nonlinear systems[J].Control Engineering of China,2021,28(9):1893-1901.
[7] 王洪亮,周洁,罗灵琳.基于LQR控制器的直线倒立摆研究及设计[J].机械与电子,2018,36(4):3-6.WANG Hongliang,ZHOU Jie,LUO Linglin.Study and design of linear inverted pendulum based on LQR controller[J].Machinery &Electronics,2018,36(4):3-6.
[8] 程前,李赫然,聂卓赟,等.基于微分平坦的旋转倒立摆双闭环抗扰PID控制[J].仪器仪表学报,2022,43(9):284-291.CHENG Qian,LI Heran,NIE Zhuoyun,et al.Design and analysis of disturbance rejection PID control for the rotary inverted pendulum system based on differential flatness theory[J].Chinese Journal of Scientific Instrument,2022,43(9):284-291.
[9] 陈增强,程赟,孙明玮,等.线性自抗扰控制理论及工程应用的若干进展[J].信息与控制,2017,46(3):257-266.CHEN Zengqiang,CHENG Yun,SUN Mingwei,et al.Surveys on theory and engineering applications for linear active disturbance rejection control[J].Information and Control,2017,46(3):257-266.
[10] 马永凌.基于ADRC方法的旋转倒立摆控制[J].自动化应用,2020(11):161-164.MA Yongling.Control of rotating inverted pendulum based on ADRC method[J].Automation Application,2020(11):161-164.
[11] 高强,陈莎莎,李毅.线性自抗扰控制在倒立摆系统的实现[J].电气传动,2014,44(10):49-53.GAO Qiang,CHEN Shasha,LI Yi.Application of ladrc on inverted pendulum system[J].Electric Drive,2014,44(10):49-53.
[12] 吴敏,肖志坚,尚猛.基于改进鲨鱼优化算法的倒立摆自抗扰控制研究[J].微电机,2019,52(9):92-97.WU Min,XIAO Zhijian,SHANG Meng.Research on adrc of inverted pendulum based on improved shark smell optimization algorithm[J].Micromotors,2019,52(9):92-97.
[13] 史乐珍,王华,洪荣晶.基于差分进化算法的旋转倒立摆线性自抗扰控制[J].南京工业大学学报(自然科学版),2019,41(1):89-95,111.SHI Lezhen,WANG Hua,HONG Rongjing.Differential evolution based linear auto disturbance rejection control of rotary inverted pendulum[J].Journal of Nanjing Tech University(Natural Science Edition),2019,41(1):89-95,111.
[14] 杨文奇,卢建华,姜旭,等.基于改进ESO的四旋翼姿态自抗扰控制器设计[J/OL].系统工程与电子技术,2022,44(12):3792-3799.YANG Wenqi,LU Jianhua,JIANG Xu,et al Design of quadrotor attitude active disturbance rejection controller based on improved ESO[J].Systems Engineering and Electronics,,2022,44(12):3792-3799.
[15] GAO Z Q.Scaling and bandwidth-parameterization based on control tuning[C]//Proceedings of the American Control Conference.Denver,Colorado:IEEE,2003:4989-499.
[16] 武利强,韩京清.直线型倒立摆的自抗扰控制设计方案[J].控制理论与应用,2004(5):665-669,688.WU Liqiang,HAN Jingqing.Active disturbance rejection controller scheme for the linear inverted pendulum[J].Control Theory &Applications,2004(5):665-669,688.