0 引言
结构物入水冲击现象在工程领域中十分常见,如舰船穿浪砰击、武器高速入水以及飞行器迫降于水面等。当结构物与水面接触时,流体动力学表现出显著的非线性特征,流体与结构物之间的相对运动会在极短的时间内引发剧烈的相互作用力,这种作用力产生的巨大冲击载荷会迅速转化为强烈的压力波和加速度,从而对结构物的运动稳定性、仪器的灵敏度以及整体的结构安全性带来重要影响。
求解结构物入水冲击载荷时,考虑自由液面的翻卷、流体与结构的耦合运动等强非线性因素的数值模拟,一直是研究的重难点,边界元法由于其在处理非线性边界条件以及计算性能方面的优势越来越受到关注。Mackie[1]采用了自由液面线性化的办法处理边界条件,而Wu[2][3]假设射流薄层上的速度势是线性函数来处理薄层射流。Dobrovol’skaya[4]忽略重力效应并假设了入水恒速,取自相似解做初始解,通过把入水问题转化为求解f(t)的积分方程,给出了第一个完整解;Zhao和Faltinsen[5]在Dobrovol’skaya[4]的基础上采用边界元法在时域内求解了问题,并提升了计算精度,但是对薄层射流做了切断处理并用线性单元连接,这样做可能引起局部数值波动。Mackie[6]在研究入水问题时不考虑流体重力,此时自相似解存在。当考虑流体重力时,自相似解不再存在因而必须在时域下求解,Sun等[7]基于边界元法研究了考虑流体重力因素时冲击压力情况,得出了入水时间较短时影响较小,但随着时间的增长,其影响变得明显。Wu[8]基于高阶边界元法研究了变速入水问题,保证了自由液面射流上的速度势和速度的连续性。Lu[9]采用边界元法和有限元法求解了流体和结构物的耦合方程,假设了水面是平静的且速度势为零,这中处理办法在自由入水中或其他有射流的流固耦合情形中可能存在问题。Semenov[10]用积分曲线法对求解了非对称楔形体垂直进入静水面问题,Xu等[11]基于边界元法分析了二维非对称楔形体匀速斜入水的水动力问题,以上研究基于自相似解只考虑了恒定入水速度的情形。Xu[12]在柱坐标系中求解锥体自由落水问题,流体微分方程转化为研物面轴向积分,但对数值计算的处理又提出了挑战,需要进一步解决耦合条件下网格划分与数值传递的难题。Dong[13]基于边界元法和落体试验法,在考虑重力和自由液面非线性变形的前提下研究了刚性和弹性楔形体的入水问题。对于入水问题中的壁面效应,于鹏垚[14]和Li[15]分别采用边界元法和有限体积法开展了相关研究,研究得到有限流域下壁面效应对冲击载荷的变化也存在一定影响。
以上研究中,考虑自相似解研究恒速入水问题较多,对于时域下的运动耦合性研究有限。考虑自由面的卷曲飞溅,计算时在网格划分与重构、数值稳定与传递方面存在一定困难,并且在射流根部存在数值振荡,因而通常对其作线性化处理,这样做并不能真实反映自由液面对载荷的影响。另外,当入水过程中随着时间的递进,流体重力因素的影响和壁面效应的影响也不应简单忽略。因此,本文中考虑了自由液面变形的非线性因素,建立满足全非线性边界条件的数学模型,按时间步进考虑了重力因素和自由液面飞溅等,借鉴Wu[2]提出的拓展坐标系的方法,对自由液面边界条件进行网格更新。通过开展自由落体试验验证数值方法的可靠性,进一步讨论了流体重力、底升角和壁面效应对冲击载荷的影响。
1 全非线性边界元法基本理论与数值算法
1.1 控制方程和边界条件
针对二维楔形体结构的入水问题,建立图1所示的数学模型。在笛卡尔坐标系中,坐标原点O建立在水平面上与楔形体轴线的交点。二维对称楔形体以实时运动速度V垂直向下入水,定义入水深度s为楔形体尖点到原始水平面的距离,底升角为θ,Ω为流体域,SF为自由液面,SC为底部边界和侧向边界。
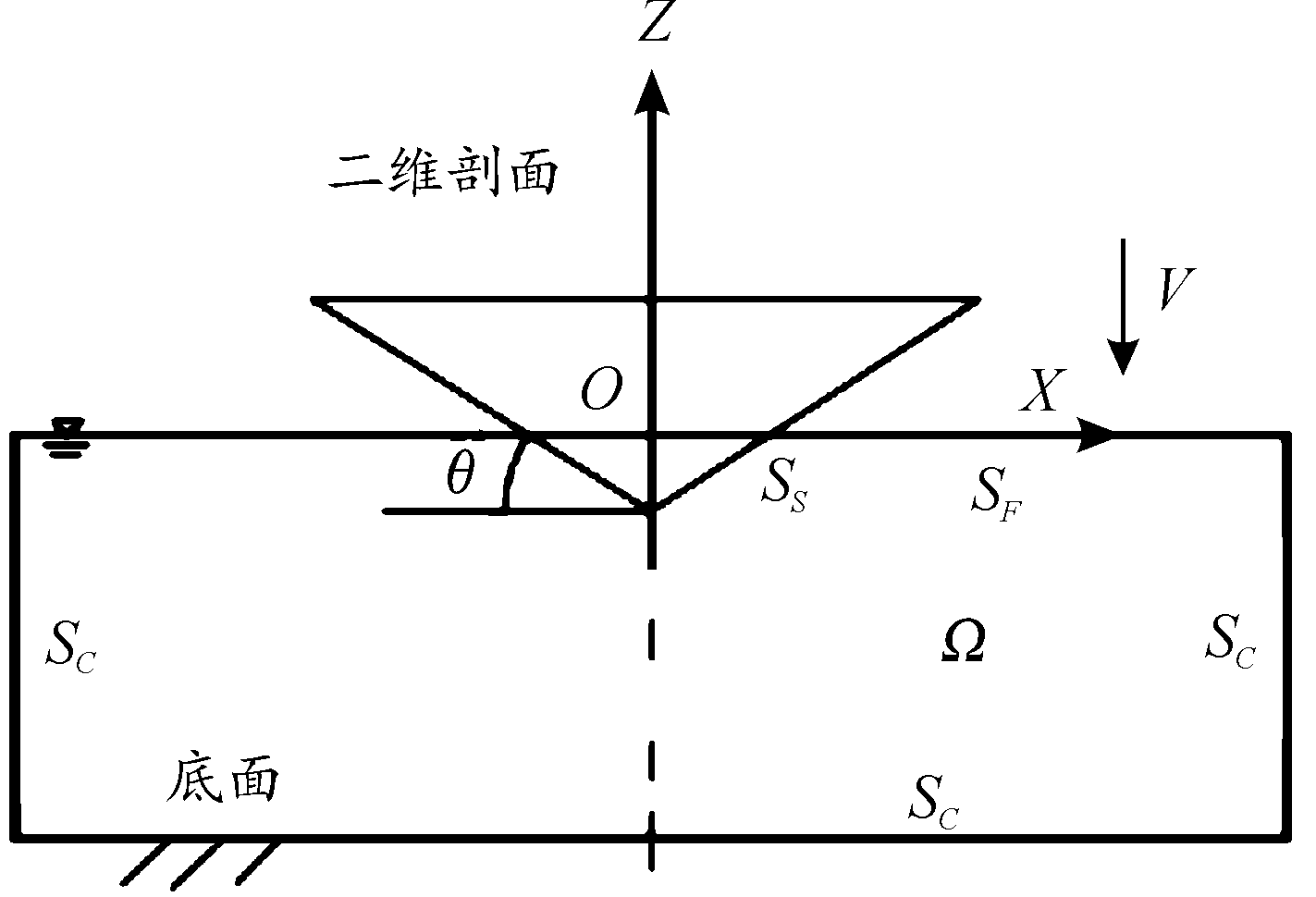
图1 楔形体入水数学模型
Fig.1 Mathematical model of wedge water entry
结构物的入水问题通常为高雷诺数水动力学问题,冲击作用时间短暂,流体粘性和压缩性对流场的影响较小,因此通常忽略流体的粘性和压缩性[16,21],因此势流理论可以较好地模拟该作用过程。基于势流理论,假设流体无粘、无旋、不可压缩,根据质量守恒定律,存在速度势φ满足Laplace方程:
▽2φ=0
(1)
物面不可穿透边界条件为
![]()
(2)
式(1)中,n=(nx,nz)物面法向量,指向流体外部为正。在自由液面SF上,欧拉运动学和动力学边界条件为
![]()
(3)
![]()
(4)
其中:ζ=ζ(x,t)为自由液面方程;g表示重力加速度,在自由液面上z=ζ(x,t)。
势流理论框架下的Laplace方程是线性的,而自由液面是非线性的,在时域步进分析之前自由液面与流动特性未知,本文中的非线性即是物面与自由液面的非线性,与自由面运动相关的线性(一阶)、二阶、三阶问题相对应。
在远离结构的流域处SC,认为流体是未被扰动的,因此有:
![]()
(5)
1.2 自由面边界条件的处理
在物理坐标系下,自由面的动网格数量迅速增加并出现网格异化,导致数值计算十分不稳定。借鉴Wu等[2]的方法,引入无量纲因子α、 β,网格的大小随α、 β变化,定义拓展坐标系:
x0=sα, z0=sβ, φ(x0,z0,t)=sV·φ(α,β,t)
(6)
其中,s=![]() V(τ)dτ表示楔形结构入水的垂向距离。
V(τ)dτ表示楔形结构入水的垂向距离。
拓展坐标系下的无量纲速度势仍然满足拉普拉斯方程。楔形体物面边界条件写为
![]()
(7)
无量纲自由面边界条件写为
![]()
(8)
![]()
(9)
式(8)中,![]() 是拓展坐标系下的自由液面方程。在控制域表面的远处,有:
是拓展坐标系下的自由液面方程。在控制域表面的远处,有:
![]()
(10)
1.3 控制方程离散
根据格林公式,将流域中无量纲拉普拉斯方程转化为整体边界的积分方程:
![]()
(11)
式(11)中:A(p)为p点处的立体角;rpq是指从p到q的距离,积分在流域封闭边界上进行,以及将其离散为一系列线性单元,在这些单元中的变量被假定为不同的线性程度,因而有:
![]()
(12)
![]()
(13)
其中:r为方位向量;u为局部内坐标,在每一个单元处其从节点k=1的0值到节点k=2的1值变化;hk(u)是满足 h1(u)=1-u和h2(u)=u的形函数。将式(12)和式(13)代入式(11)中,得:
![]()
(14)
Ne是整体边界的单元总数,lj是单元j的差长度,将方程式(14)进一步表示成矩阵形式:
![]()
(15)
式(15)中,Nd是在整个边界上的全部节点数。从边界条件可得知结构表面速度势∂φ/∂n的法向导数和在每一时间步中自由表面的速度势φ。将已知项移到式(15)的右端,得到:
![]()
(16)
式(16)中:下标f 指自由表面;b指的是包含远方边界在内的结构表面。
1.4 局部坐标系下的自由面边界条件
在楔形体入水过程中,自由面形状发生飞溅、卷曲或破碎,自由面上节点的![]() 可能趋向于无限大。因此为解决这一难题,引入局部坐标系
可能趋向于无限大。因此为解决这一难题,引入局部坐标系![]() 其中
其中![]() 切向于自由面,
切向于自由面,![]() 指向自由面外法向,并且将局部坐标系应用在整个自由面上(注:下文中带^的参数均指代在局部坐标系下的变量)。局部坐标系和笛卡尔坐标系的关系为
指向自由面外法向,并且将局部坐标系应用在整个自由面上(注:下文中带^的参数均指代在局部坐标系下的变量)。局部坐标系和笛卡尔坐标系的关系为
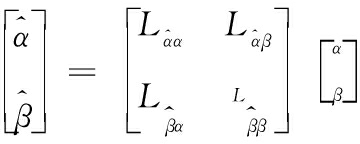
(17)
该坐标系下,自由表面运动学条件写为
![]()
(18)
式(18)中,![]() 说明节点在物理坐标系下速度为0,但在拓展坐标下
说明节点在物理坐标系下速度为0,但在拓展坐标下![]() 因此可以在拓展坐标系下限制在
因此可以在拓展坐标系下限制在![]() 方向上的位移。当
方向上的位移。当![]() 时得到:
时得到:
![]()
(19)
式(18)和式(19)用来计算自由液面,前者用于计算远处的自由表面,后者用于计算楔形体物面附近处的自由液面。因此,则求得速度势为
![]()
(20)
1.5 运动方程的解耦
楔形体的即时速度和位移由未知的加速度决定,加速度由作用于楔形体表面的水动力决定,因而需要进一步对运动方程解耦。由伯努利方程计算压力为
![]()
(21)
Wu[2]给出了一种间接求解方法,通过把![]() 看作一个调和函数,仍然满足:
看作一个调和函数,仍然满足:
▽2φt=0
(22)
结构的加速度由流体水动力决定,流体水动力通过对结构表面压力积分得到:
![]()
(23)
![]()
(24)
其中: G为楔形体的重力,F为流体力,p为压力。压力p与速度V和加速度![]() 有关,为了求解式(21)、式(23)、式(24),构造辅助函数
有关,为了求解式(21)、式(23)、式(24),构造辅助函数![]() 定义:
定义:
![]()
(25)
仍然满足:
![]()
(26)
结构表面边界条件可以写成如下形式:
![]()
(27)
在自由表面,满足:
![]()
(28)
在拓展坐标系中求解域的边界节点的无量纲辅助函数![]() 和一阶导数
和一阶导数![]() 后,则流体作用力F即可求得:
后,则流体作用力F即可求得:
![]()
(29)
式(29)中,![]() 是附加质量项。
是附加质量项。
2 楔形体入水冲击试验
2.1 试验装置及工况
试验装置采用底升角θ=45°的钢制楔形体模型,尺寸为1.5 m×0.9 m×0.75 m,总质量为550 kg。为确保模型具有足够刚度防止变形,试件外板厚度为10 mm。为保证二维冲击效应,试件两侧设置挡板,并在斜底板中间对称布置了压力传感器。楔形体试件模型见图2,试验根据入水初速度来设计工况,通过改变自由落体的高度获得对应的入水初速度。落体试验各工况详情见表1。
表1 楔形体模型工况设计
Table 1 Working condition design of wedge model
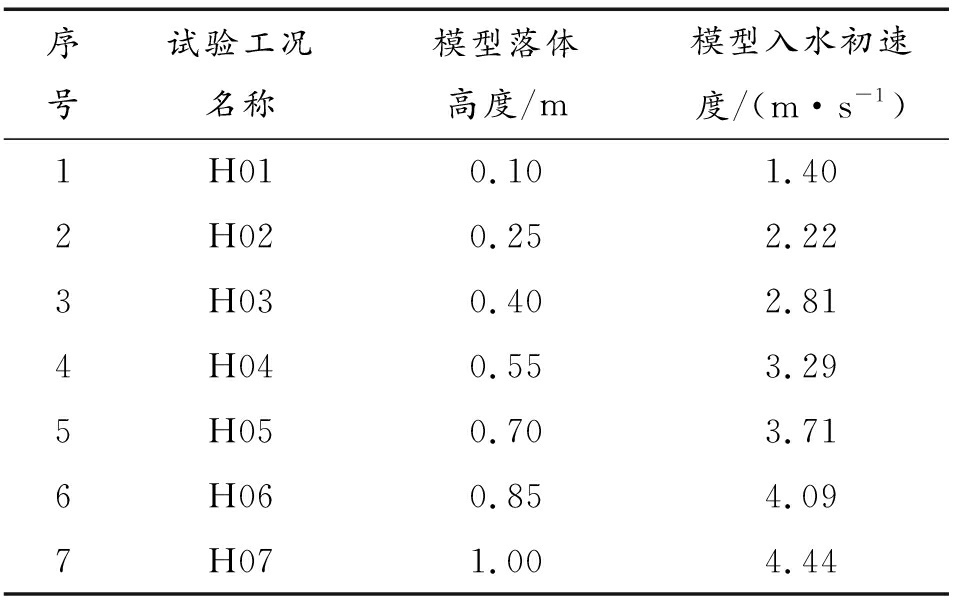
序号试验工况名称模型落体高度/m模型入水初速度/(m·s-1)1H010.101.402H020.252.223H030.402.814H040.553.295H050.703.716H060.854.097H071.004.44

图2 楔形体试件
Fig.2 Wedge specimen
2.2 试验结果分析
为了检验试验的稳定性与可重复性,选取相同工况重复3次。试验监测了楔形体入水的物理量压力和位移时历变化,消除数据中的高频数据做低通滤波处理,取滤波频率为250 Hz。图3(a)展示了在落体高度H=0.55m下P3测点的3次重复试验数据对比,结果表明测量系统的稳定性良好。将测量的冲击压力峰值作无因次化处理,设FP为冲击压力峰值,定义楔形体冲击压力系数:
![]()
(30)

图3 试验稳定性校验
Fig.3 Test stability verification
式(30)中:ρ为流体的密度;VP为冲击压力达到峰值时楔形体的速度。图3(b)根据试验结果计算了P1—P5测点在不同工况下的冲击压力系数。
由图3(b)得到,每个测点的冲击压力系数相对稳定,受初速度大小的影响较小;对于P1、P2、P3、P4、P5个测点从下而上分布,在入水初过程中随着入水深度的增加,湿表面与自由液面不断扩展,流体的水动压力和射流的影响逐步有所影响,因而冲击压力系数出现微弱的变化,但整体相差不大。以数据最稳定的P4测点为例,计算得到的冲击压力系数k为1.80,与Von Karman理论中![]() (β≥10°时)的计算结果(k=1.57)相近,经验公式的近似计算结果偏小,是因为基于自由面线性化处理的假设。
(β≥10°时)的计算结果(k=1.57)相近,经验公式的近似计算结果偏小,是因为基于自由面线性化处理的假设。
2.3 数值计算验证
以H04工况为例,图4将P3、P5测点的试验结果与数值模拟结果进行对比验证。
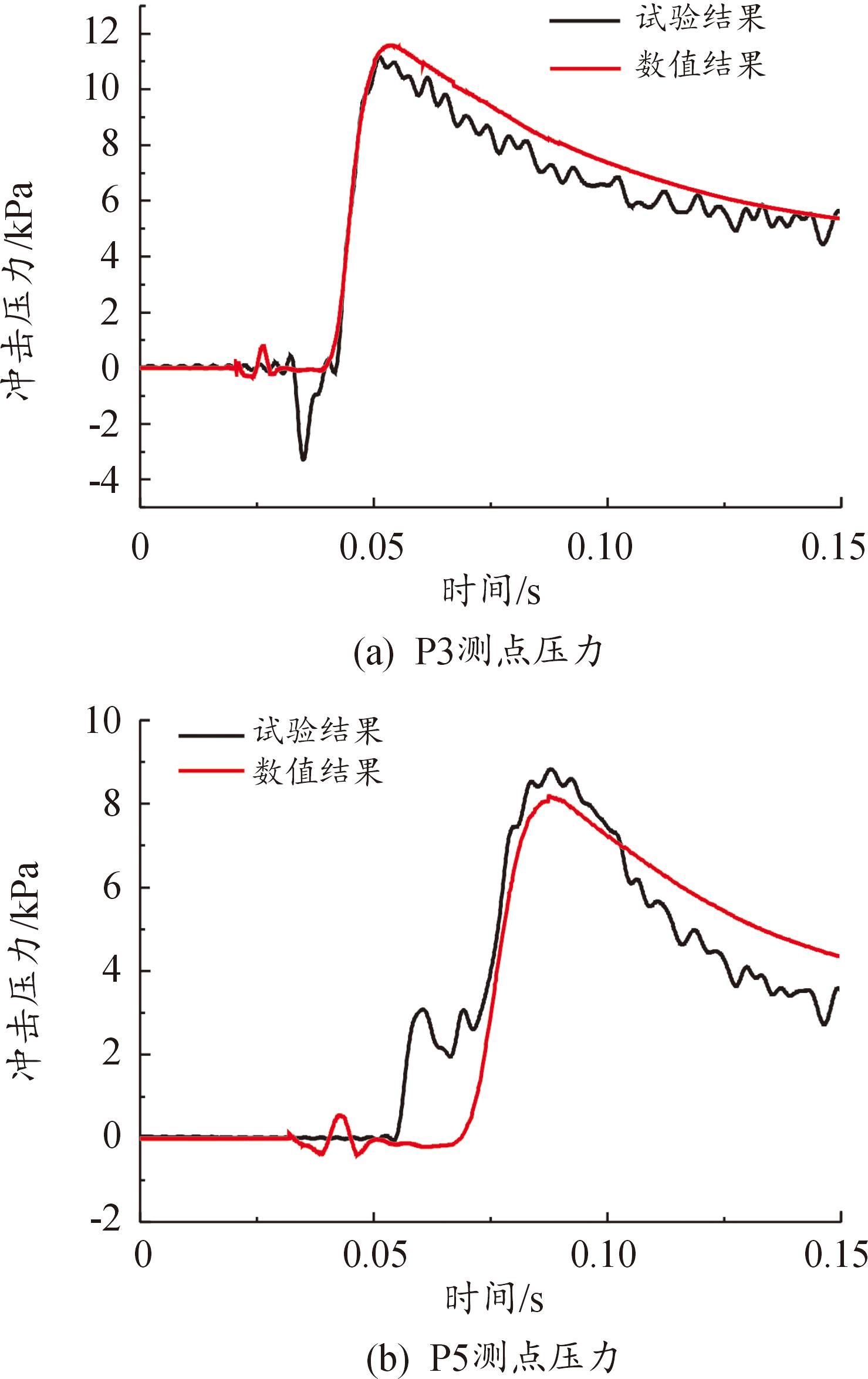
图4 试验结果与数值结果对比
Fig.4 Comparison of experimental results with numerical results
图4表明:数值模拟和试验方法有较好的一致性,冲击压力峰值非常接近。试验值比数值计算结果略低,原因是数值模型假设为“理想刚性”的,试验试件并非理想刚性而表现出一定“弹性效应”;P5点在达到压力峰值后,压力降比数值计算的结果更明显,这是因为试验试件尺度有限而存在“尺度效应”,在楔形体入水过程的后期阶段,流体流经该测点后马上发生流动分离,相比尺度无限大的数值计算模型(不考虑流动分离),其压力明显降低。
总体来看,落体试验结果验证了本数值计算方法的可靠性和有效性。
3 冲击载荷特性研究
3.1 流体重力的影响
图5计算了楔形体在H07工况即入水初速度为4.44 m/s时,考虑流体重力和不考虑流体重力时楔形体物面的载荷分布。在楔形体半宽上定义无量纲距离α=x/s,无量纲冲击压力CP=FP/(0.5*ρV2),x为楔形体物面上计算点的水平坐标。
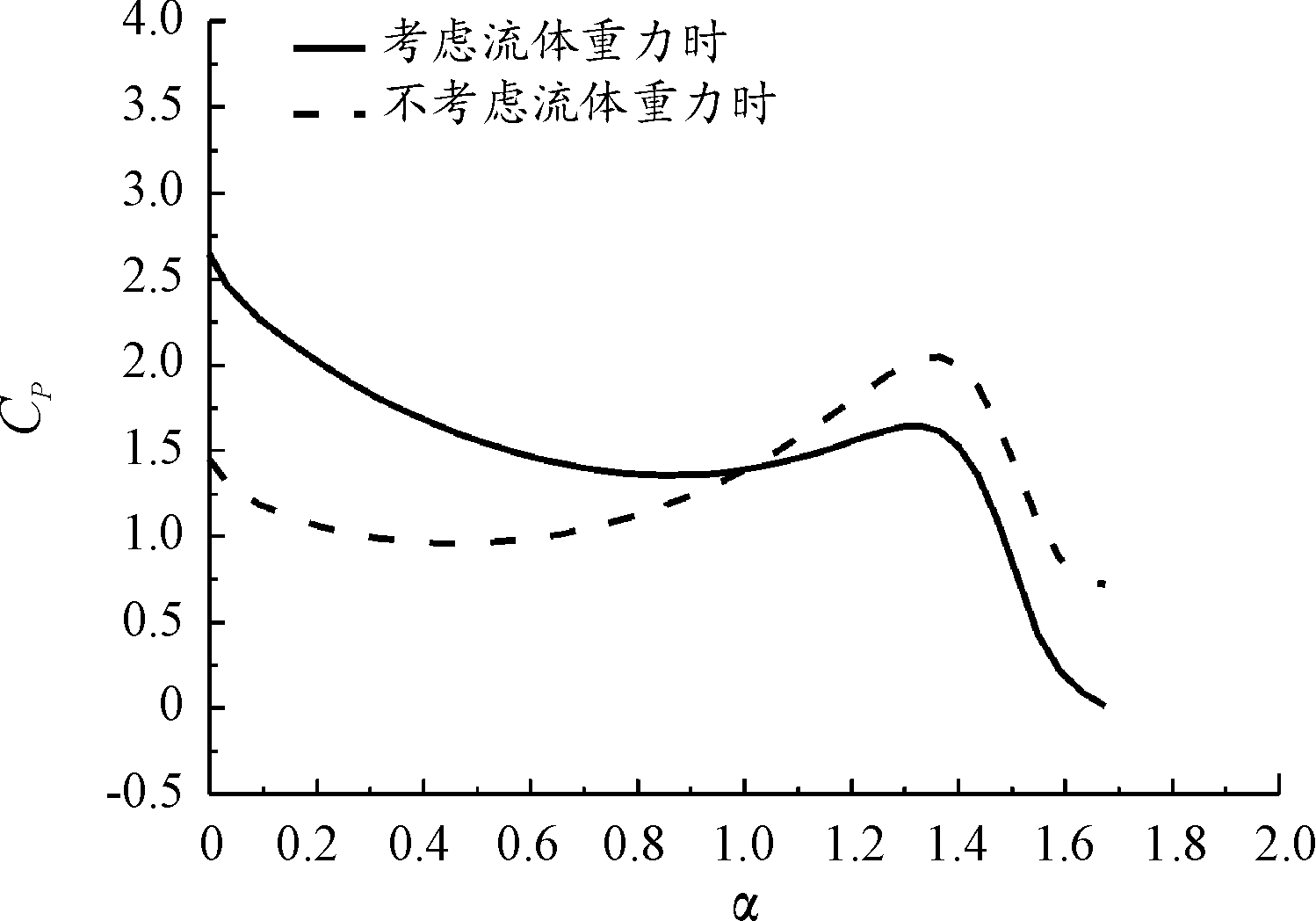
图5 流体重力对冲击载荷的影响
Fig.5 Influence of fluid gravity on impact load
由图5得知,不论是否考虑流体重力因素,在尖点到射流根部之间的区域保持较高的压力,经过射流根部时,此时α=1.3,冲击压力都出现了二次峰值,最后冲击压力快速降至零。区别在于:考虑流体重力因素时,冲击压力最大值出现在楔形体尖点;不考虑流体重力时,冲击压力最大值出现在射流根部。随着射流的发展,冲击压力迅速下降,在α=1.6的位置处降为零,说明到达该位置后射流开始与楔形体物面分离。另外,考虑流体重力因素时,楔形体上的冲击压力有明显差异,当α≤1时,即水平面以下的物面位置,考虑流体重力时的冲击压力明显高于不考虑流体重力时的冲击压力,这部分差值正是考虑自由液面抬升的静水压力;当α>1时,不考虑重力时的冲击压力高于考虑流体重力时的冲击压力,这是因为流体重力导致了飞溅的射流根部的冲击压力下降。
3.2 底升角的影响
入水冲击压力与楔形体底升角θ有着密切关系。选取15°、25°、30°、35°、45°五种底升角的楔形体进行进一步分析。在保证模型质量和尺寸不变的情况下,设定入水初速度为4.44 m/s。用弧度制底升角![]() 表示角度,以P3点为算例,计算结果如图6所示。
表示角度,以P3点为算例,计算结果如图6所示。

图6 底升角的影响
Fig.6 The influence of deadrise angle on impact pressure
从图6(a)和图6(b)得到,当底升角从45°减至15°时,冲击压力峰值显著增加,由18.52 kPa增大至271.24 kPa,增幅超过13倍;同时,加速度由-4.24 m/s2激增至-321.24 m/s2,增长幅度接近80倍,较小底升角的结构在入水冲击中时更早达到峰值压力。这些变化表明,冲击压力和加速度对底升角十分敏感,较小底升角的结构在发生入水冲击时遭受的冲击现象更为剧烈。通过多项式曲线优化拟合,得到无量纲冲击压力与底升角的关系方程:
![]()
(31)
式(31)揭示了冲击压力峰值对底升角的高度敏感性,且冲击压力峰值与底升角大小之间存在非线性关系。随着![]() 值的减小,
值的减小,![]() 峰值的增长速率加快,表明钝型楔形体(具有较小底升角)的冲击压力迅速增加;而随着
峰值的增长速率加快,表明钝型楔形体(具有较小底升角)的冲击压力迅速增加;而随着![]() 值的增大,则
值的增大,则![]() 峰值的增长速率减缓,表明在相同速度下,尖锐型楔形体在冲击入水时所承受的冲击载荷相对较小且变化并不明显。可用该方程可以绘制相关图表,定量分析不同底升角的结构物入水时所受的冲击压力。
峰值的增长速率减缓,表明在相同速度下,尖锐型楔形体在冲击入水时所承受的冲击载荷相对较小且变化并不明显。可用该方程可以绘制相关图表,定量分析不同底升角的结构物入水时所受的冲击压力。
3.3 水域深度的影响
本节内容主要探讨由底面反射给自由表面的扰动,对楔形体入水冲击载荷的影响,即所谓的壁面效应[14-15]。本部分着重分析了楔形体入水初速度和底升角在不同水深下的壁面效应,选取初速度为V =1、2、4 m/s 3种工况,考虑了15°、30°和45°3种底升角模型,其他参数保持与前述研究一致。用无因次量纲深度![]() 表示楔形体入水深度S0与水域深度的比值,分别计算了水深为20、8、4、2、1、0.8 m时的无量纲冲击压力峰值,计算结果如图7所示。
表示楔形体入水深度S0与水域深度的比值,分别计算了水深为20、8、4、2、1、0.8 m时的无量纲冲击压力峰值,计算结果如图7所示。
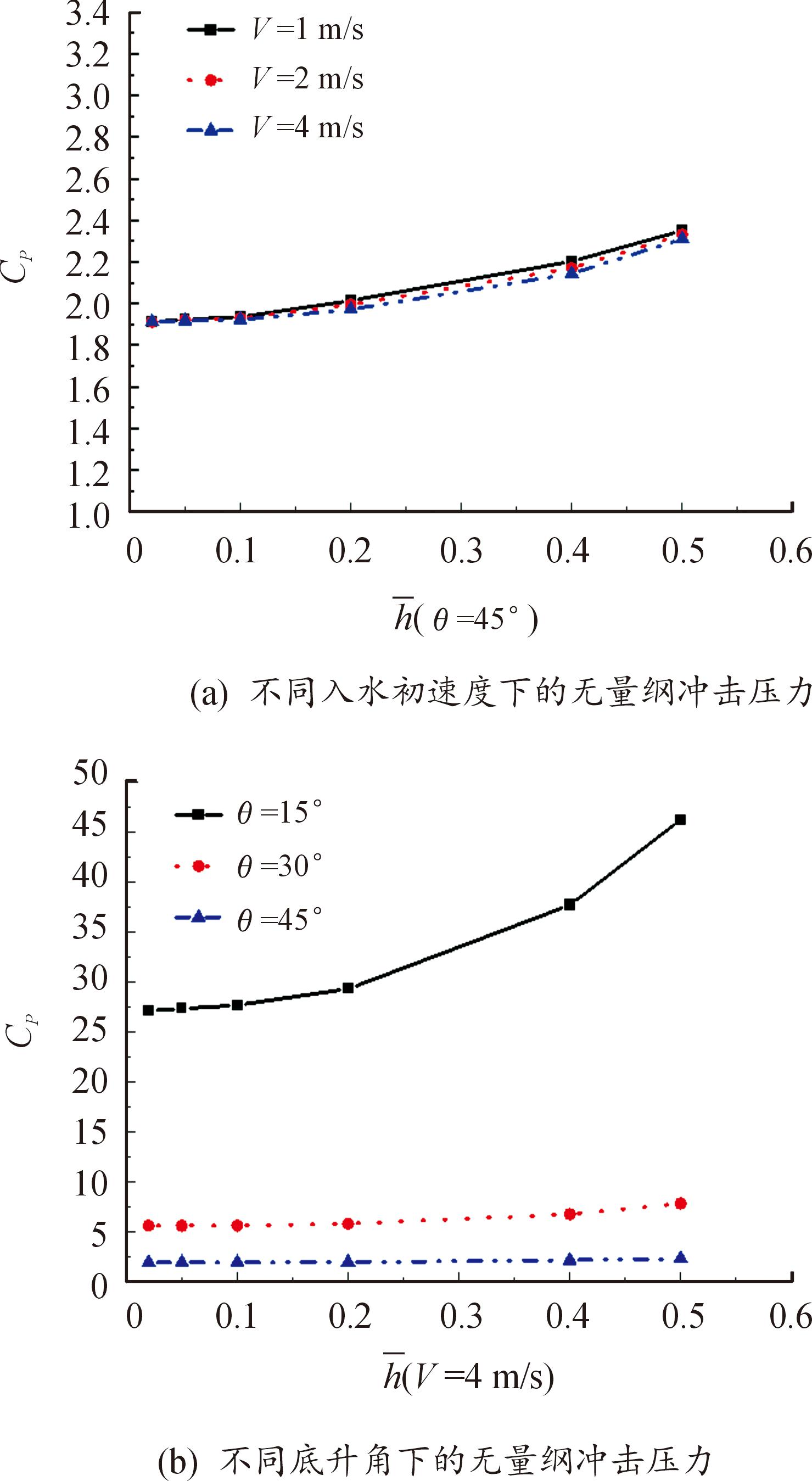
图7 壁面效应对冲击载荷的影响
Fig.7 The influence of wall effect on impact load
从图7(a)中看到,在底升角为45°时,楔形体以不同初速度入水时无量纲冲击压力随无量纲深度的变化。结果表明,在1 m/s与4 m/s的入水速度下,在最小水深条件下冲击压力峰值的差异为5.45%,从而可以推断壁面效应与入水初速度基本无关。当入水初速度为4 m/s时,在![]() 的情况下,最大冲击压力变化了3.03%;当
的情况下,最大冲击压力变化了3.03%;当![]() 时,变化了10.68%;当
时,变化了10.68%;当![]() 时,变化了21.89%。因此得到,当水深超过楔形体入水深度的5倍时,壁面效应不明显;当水深在楔形体入水深度的3.33倍到5倍之间时,壁面效应开始显现;而当水深小于3.33倍时,壁面效应尤其明显。
时,变化了21.89%。因此得到,当水深超过楔形体入水深度的5倍时,壁面效应不明显;当水深在楔形体入水深度的3.33倍到5倍之间时,壁面效应开始显现;而当水深小于3.33倍时,壁面效应尤其明显。
在图7(b)中,入水初速度为4 m/s时,不同底升角楔形体入水时无量纲冲击压力随无量纲深度的变化。在无因次量纲深度![]() 时(即水深是楔形体入水深度的2倍),15°、30°、45°底升角的楔形体遭受的冲击压力峰值变化率分别为41.3%、28.16%、21.89%,从曲线走势上(即拟合曲线的导数或斜率)也可以直观发现,小角度的无量纲压力峰值爬升的更快,这表明较小的底升角在水深方向上的壁面效应更为显著;同时这些结果也支持了在不同水深区间(h≥5S0、1.33S0≤h<5S0、h<1.33S0)壁面效应逐渐增强的结论。
时(即水深是楔形体入水深度的2倍),15°、30°、45°底升角的楔形体遭受的冲击压力峰值变化率分别为41.3%、28.16%、21.89%,从曲线走势上(即拟合曲线的导数或斜率)也可以直观发现,小角度的无量纲压力峰值爬升的更快,这表明较小的底升角在水深方向上的壁面效应更为显著;同时这些结果也支持了在不同水深区间(h≥5S0、1.33S0≤h<5S0、h<1.33S0)壁面效应逐渐增强的结论。
4 结论
1) 基于边界元方法考虑了自由面的非线性因素,通过引入拓展坐标系有效地解决了数值计算的稳定性和传递性问题;借助辅助函数法解耦了时域中运动方程,获得了楔形体物面上的压力分布。通过与实验结果的对比验证,论证了全非线性边界元法能够满足求解问题的可靠性要求。
2) 流体重力对楔形体表面冲击压力产生了明显的影响。45°底升角楔形体的入水冲击压力主要分布在1.6倍入水深度的半宽区域内,超过该区域后因射流分离而逐步降为零。除了楔形体尖端处出现压力峰值外,射流根部也观察到了压力极值点。另外,定量分析并验证了楔形体入水冲击压力受到底升角的非线性影响的事实。
3)壁面效应与入水初速度无关,但与楔形体底升角有一定关系,较小的底升角会导致更为明显的壁面效应。对于45°底升角的楔形体,当水深大于入水深度的5倍时,壁面效应不明显;当水深大于入水深度的3.33倍而小于5倍时,壁面效应开始显现;当水深小于入水深度的3.33倍时,壁面效应变得非常显著,此时,结构物入水时的壁面效应应当受到充分关注。
[1]MACKIE A G.A linearized theory of the water entry problem[J].Quarterly Journal of Mechanics and Applied Mathematics,1962,15(2):137-151.
[2]WU G X,SUN H,HE Y S.Numerical simulation and experimental study of water entry of a wedge in free fall motion[J].Journal of Fluids and Structures,2004,19(3):277-289.
[3]SUN S L,WU G X.Fully Nonlinear simulation for fluid/structure impact:a review[J].Journal of Marine Science and Application,2014(13):237-244.
[4]DOBROVOL' SKAYA Z N.On some problems of similarity flow of fluid with a free surface[J].Journal of Fluid Mechanics,1969,36 (4);805-829.
[5]ZHAO R,FALTINSENO.Water entry of two-dimensional bodies[J].Journal of Fluid Mechanics,1993,246:593-612.
[6]MACKIE A G.Gravity effects in the water entry problem[J].Journal of the Australian Mathematical Society,1964,5(4); 427-433.
[7]SUN S Y,SUN S L,WU G X.Oblique water entry of a wedge into waves with gravity effect[J].Journal of Fluids and Structures,2015,52:49-64.
[8]WUGX.Numerical simulation for water entry of a wedge at varying speed by a high order boundary element method[J].Journal of Marine Science and Application,2012,36 (2):143-149.
[9]LU C H,HE Y S,WU G X.Coupled analysis of nonlinear interaction between fluid and structure during impact[J].Journal of Fluids and Structures,2000,14(1);127-146.
[10]SEMENOV Y A,IAFRATI A.On the nonlinear water entry problem of asymmetric wedges[J].Journal of Fluid Mechanics,2006,547:231-256.
[11]XU G D,DUAN W Y,WU G X.Numerical simulation of oblique water entry of an asymmetrical wedge[J].Ocean Engineering,2008,35(16):1597-1603.
[12]XU G D,DUAN W Y,WU G X.Numerical simulation of water entry of a cone in free fall motion[J].Quarterly Journal of Mechanics and Applied Mathematics,2011a,64(3); 265-285.
[13]DONG C R,SUN S L,SONG H X.et al.Numerical and experimental study on the impact between a free falling wedge and water[J].International Journal of Naval Architecture and Ocean Engineering,2019(11):233-243.
[14]于鹏垚,张博然,赵勇,等.楔形体入水冲击中的壁面效应分析[J].华中科技大学学报(自然科学版),2019,47(6):73-78.YU Pengyao,ZHANG Boran,ZHAO Yong,et al.Analysis on wall effect during water entry of wedge[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2019,47(6):73-78.
[15]LI Y J,SUN S Y.Simulation of water entry into shallow water based on boundary element method[J].Ocean Engineering,2022,263;1-11.
[16]孙士丽,许国冬,倪宝玉.流体与结构砰击水动力学[M].哈尔滨:哈尔滨工程大学出版社,2014.SUN Shili,XU Guodong,NI Baoyu.Hydrodynamics of fluid/structure impact[M].Harbin Engineering University Press,2014.
[17]SUN H,FALTINSENOM.The influence of gravity on the performance of planning vessels in calm water[J].Journal of Engineering Mathematics,2007.58:91-107.
[18]孙辉,卢炽华,何友生.二维楔形体冲击入水时的流固耦合响应的实验研究[J].水动力学研究与进展,2003,18(1):104-109.SUN Hui,LU Chihua,HE Yousheng.Experimental research on the fluid-structure interaction in water entry of 2D elastic wedge[J].Chinese Journal of Hydrodynamics,2003,18(1):104-109.
[19]WU G X.Hydrodynamic force on a rigid body during impact with liquid[J].Journal of Fluids and Structures,1998(12):549-559.
[20]WAGNER V H.Phenomena associated with landing and sliding on liquid surfaces[J].National Advisory Committee for Aeronautics,1932,321:145-162.
[21]BATCHELOR G K.An introduction to fluid dynamics[M].London:Cambridge University Press,1967.