0 引言
装药水中爆炸产生冲击波、气泡运动和二次压力波,水中爆炸压力信号为瞬时突变非平稳信号,其频率成分复杂,不同当量装药在水中不同条件下爆炸,压力信号呈现不同的特征,并会导致舰艇等目标产生不同的冲击响应,水中爆炸压力作为舰艇抗冲击试验中的输入载荷,其信号特征分析是舰船结构和设备分析的前提。科研人员对水中爆炸信号特征开展了相关研究,李国华在“气泡运动与舰船设备冲击振动关系的试验验证”一文中通过研究认为,在浮动冲击平台水下爆炸试验中发现水下爆炸气泡膨胀产生的滞后流是使安装频率为数十赫兹的舰船设备产生冲击振动的主要能量[1];谢耀国对0.5 kg TNT药包在水池中自由场爆炸条件下爆炸产生的自由场压力信号进行了分析,得到的结论是冲击波时段在8 kHz以下频段集中了超过90%的能量,分析结果对舰船结构及设备的抗冲击防护具有借鉴意义[2]。
装药沉底爆炸时受到装药当量变化和海底边界条件影响,水中爆炸压力信号呈现出与自由场条件下爆炸所不同的特征[3-12],装药当量不同对压力信号时频特征会产生影响,压力信号时频特征和能量分布会发生明显变化。采用小波分析方法,对实际测量的压力信号进行多层时频分解和信号重构,分析不同频段下和不同时段下的信号特征、计算不同频段和时段下的信号能量分布,得到大当量装药沉底爆炸条件下压力信号的时频特征信息,明确舰艇结构和设备抗冲击响应分析中应重点关注的频段和时段。
1 沉底爆炸试验
爆炸试验在海上实施,爆源为1 000 kg TNT装药沉底布放,距爆源一定距离的水中悬浮布放压力传感器,采集仪布设于抗冲击载体,传感器连接低噪声测量电缆接入采集仪,爆炸时刻实时采集记录压力时程数据。
装药水中爆炸一般包括3个时段:第1时段为水中爆炸冲击波时段;第2时段为爆轰产物形成气泡,当其膨胀速度小于水中声速、气泡不断膨胀从而推动水质点做径向运动而形成滞后流时段;第3时段为气泡脉动收缩而形成的二次压力波时段。
从试验测量得到的压力时程数据可以看到,数据包括了冲击波、滞后流和气泡收缩的二次压力波3个时段,气泡脉动周期约800 ms,略大于理论计算公式;从时程曲线可以看到沉底爆炸所形成的二次压力波峰值很小,说明沉底爆炸时海底边界对气泡存在吸附作用。对压力时程数据的分析包括了冲击波、滞后流和二次压力波3个时段。图1为沉底爆炸压力时程曲线。
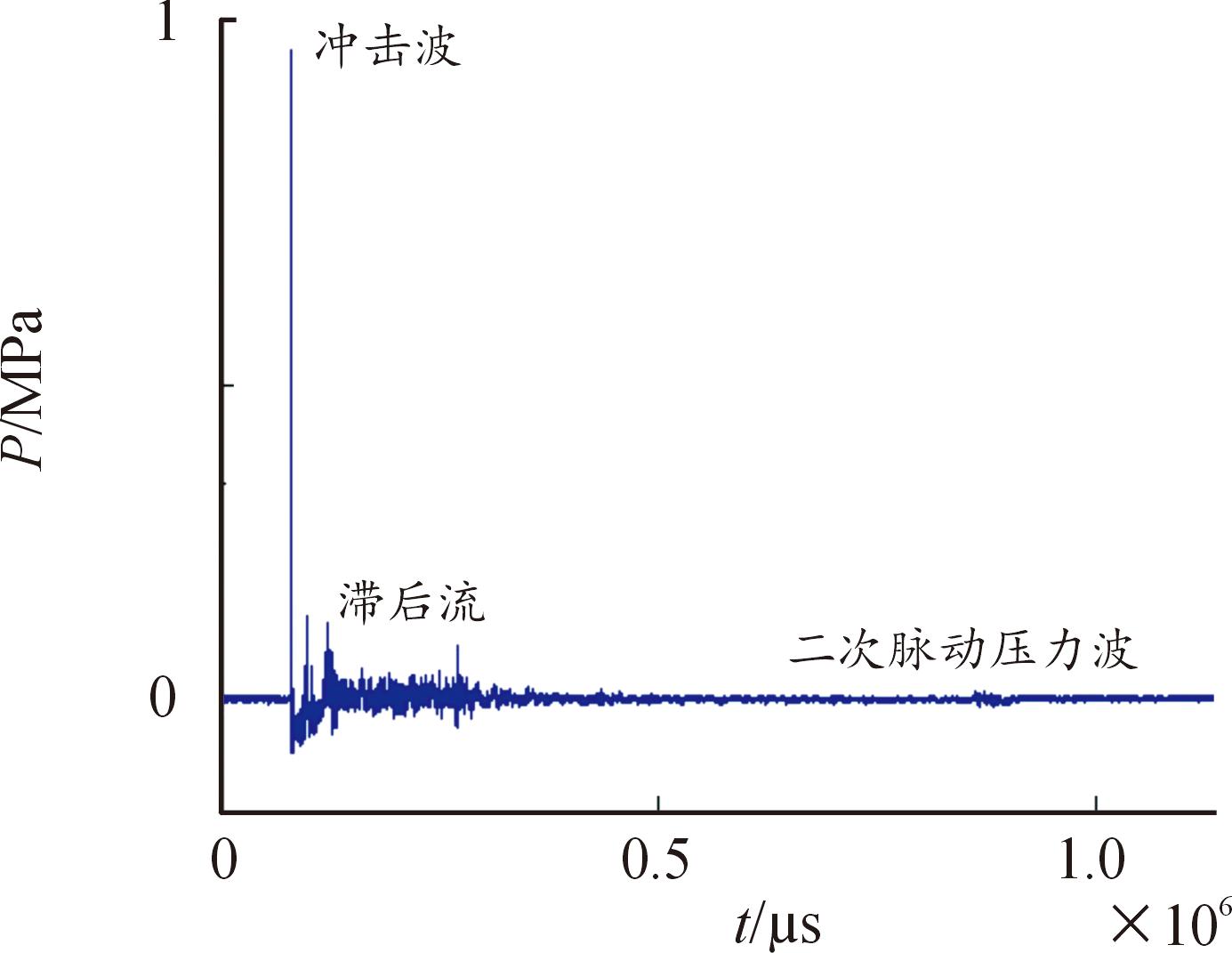
图1 沉底爆炸压力时程曲线
Fig.1 Pressure curves of underwater bottom explosive
2 小波分析
小波分析可用于分析瞬时时变信号[13-15],能从信号中提取时间和频率信息,通过伸缩和平移等运算功能对信号进行多尺度细化分析。小波变换使用一个有限长小波基取代傅里叶变换中的无限长三角函数,是中间振荡、双边衰减的波形,可以进行缩放拉伸,使小波变换具有了很高的时间上的频率分辨力,信号分解分段重构后不会丢失时间信息,适用于水中爆炸的复杂时变信号分析。
原始爆炸信号经小波分解后,可得到由高到低各分析频段内的小波系数,如果将信号进行n层分解,即得到n+1个小波系数,对应n+1个频段,图2为小波分解结构框图。

图2 小波分解结构框图
Fig.2 Wavelet decomposition structure
通过对小波分解后各频段的小波系数重构可得到对应分解频段的压力时程信号,得到信号各频段特征,信号重构后可以分别求出各频段对应的能量,能量计算公式为
![]()
(1)
![]()
(2)
式(1)中:Ei为小波分解后第i频段信号对应的能量;pi(t)为第i频段的小波分解信号;pij为第i频段信号pi(t)的离散点幅值;式(2)中:E为被分析爆炸信号分解重构后的总能量。
小波分解后各频段能量在分析信号总能量中的占比为
![]()
(3)
3 沉底爆炸压力载荷时频特征分析
3.1 信号小波分解与重构
小波基选择:对信号进行小波分解时需要选择合适的小波基,小波基的选取一般考虑以下几个因素:支撑长度、对称性、消失矩、正则性、相似性。dbN小波具有较好的正则性,频域的局部化能力强,频带的划分效果好;通过对几个小波基的分解结果对比显示,db8分解重构后的信号和原始信号相比误差最小。
试验中所使用的压力采集仪采样频率为1 MHz,根据奈奎斯特频率采样定理,信号分析最大频率为0.5 MHz。以实测的沉底爆炸压力信号为分析对象,采用db8小波基对信号进行小波分解,若进行n层分解,则各层频段范围计算公式为
![]()
(4)
式(4)中:Fs为实测的原始压力信号采样频率; fmax为信号分析最大频率。对原始压力信号进行11层小波分解,分解后得到由高频到低频的12个小波系数,分别为d1~d11、a11。压力信号分解后的小波系数和对应频段如表1所示。
表1 小波分解系数和对应频段
Table 1 Corresponding frequency band of wavelet decomposition
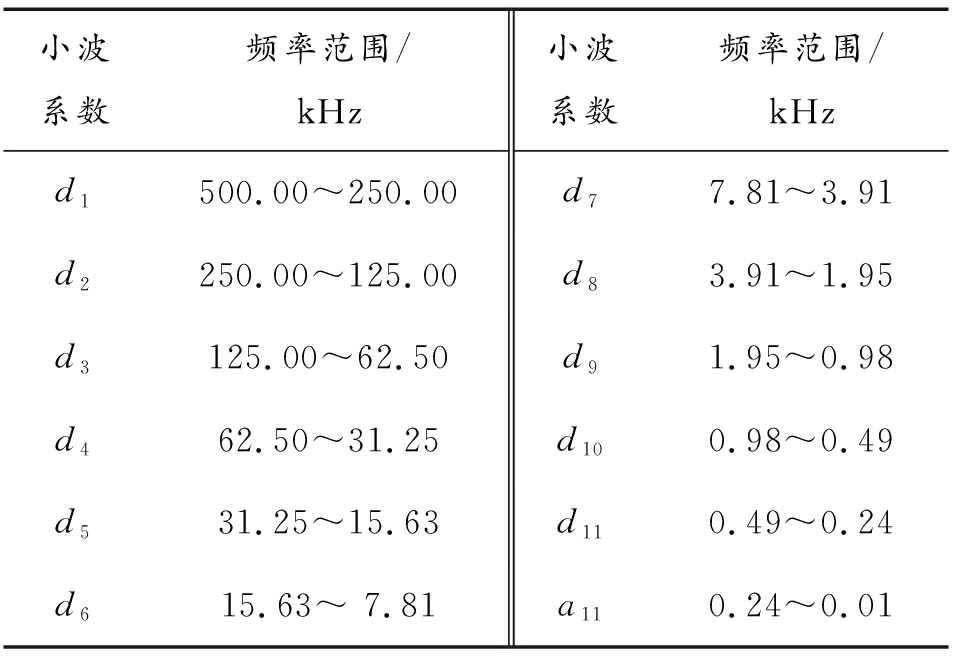
小波系数频率范围/kHz小波系数频率范围/kHzd1500.00~250.00d77.81~3.91d2250.00~125.00d83.91~1.95d3125.00~62.50d91.95~0.98d462.50~31.25d100.98~0.49d531.25~15.63d110.49~0.24d615.63~ 7.81a110.24~0.01
为验证小波分解产生的误差,对分解后的信号进行重构,将重构信号与分解前的原始信号进行对比,最大幅值误差在冲击波压力峰值处,为10-12 MPa量级;同时利用式(2)计算分解重构后的总能量,和原始信号能量比较,二者误差为0 J,说明小波分解不会导致信号失真和能量损失,选择的小波基是合适的。由于二次压力波很小,因此只取冲击波时段和滞后流时段数据绘制误差和小波分解重构图,重构信号与原始信号误差如图3所示,各频段重构压力信号如图4所示,分别对应于表1中12个频段。

图3 重构信号与原始信号误差
Fig.3 Error between reconstructed signal and original signal

图4 各频段重构压力信号
Fig.4 Reconstructed pressure signals in each frenquency band
3.2 数据处理
为分析沉底爆炸压力信号在不同频段的能量分布和压力分布,根据小波系数对各频段进行信号重构,得到12个频段压力重构信号,利用式(1)—式(3)计算各频段压力信号能量Ei和相对于总能量占比ki,以及重构后各频段压力相对于冲击波峰值压力占比kpi。压力占比分析时,由于各频段压力峰值对应的采样点位置与分解前的压力峰值采样点不完全对应,而是随着频率降低压力峰值点逐渐滞后于原信号峰值点位置,因此小波分解后取的压力值取对应于分解前压力峰值所对应的采样点压力值。表2为不同频段的能量和压力占比计算结果,图5为各频段能量和压力占比。
表2 不同频段的能量和压力占比计算结果
Table 2 Energy and pressure ratio in each frequency band

小波系数频率范围/kHzkikpid1500.00~250.000.950.08d2250.00~125.000.091.07d3125.00~62.500.1414.32d462.50~31.250.2113.06d531.25~15.630.3011.18d615.63~ 7.810.355.44
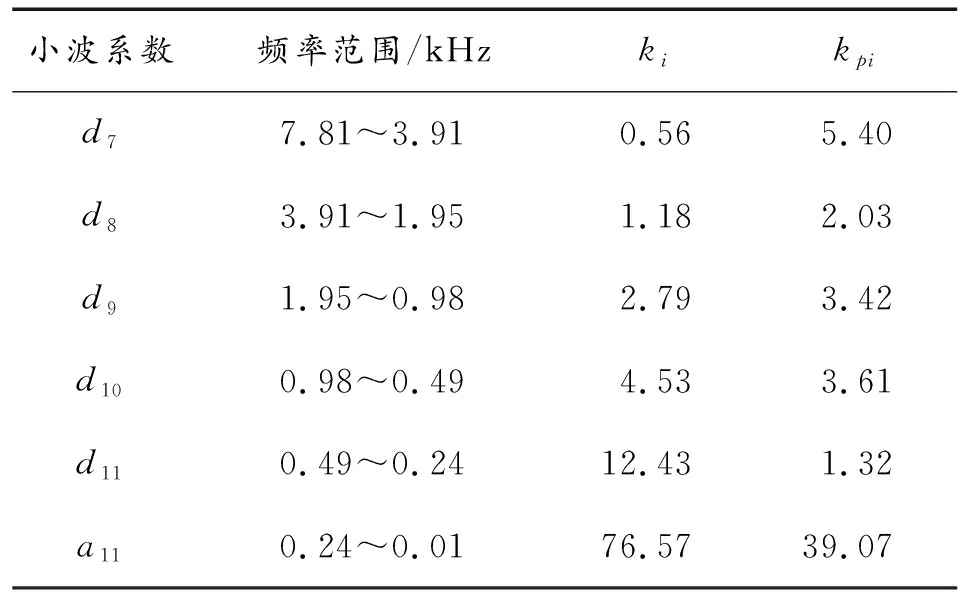
小波系数频率范围/kHzkikpid77.81~3.910.565.40d83.91~1.951.182.03d91.95~0.982.793.42d100.98~0.494.533.61d110.49~0.2412.431.32a110.24~0.0176.5739.07
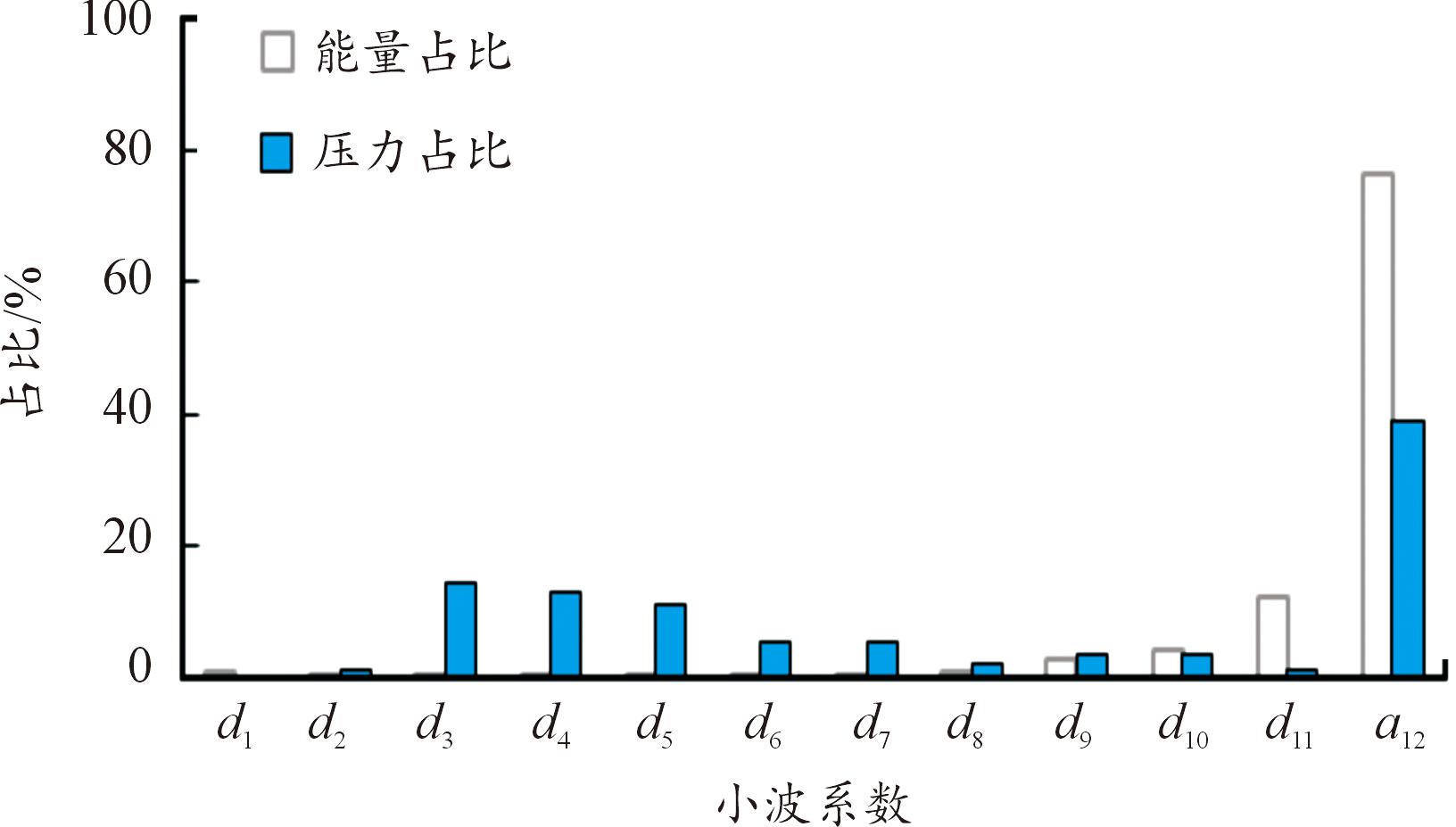
图5 各频段能量和压力占比图
Fig.5 Energy and pressure ratio in each frequency stage
再分别对冲击波时段、滞后流时段、气泡收缩后的二次压力波时段采用db8小波进行11层分解重构,计算每个时段中分解后的各频段能量占比,分别为ksi、kai、kbi。表3为各时段各频段能量占比计算结果,图6为各时段各频段能量占比。
表3 各时段各频段能量占比计算结果
Table 3 Results of energy ratio in each time period and frequency band
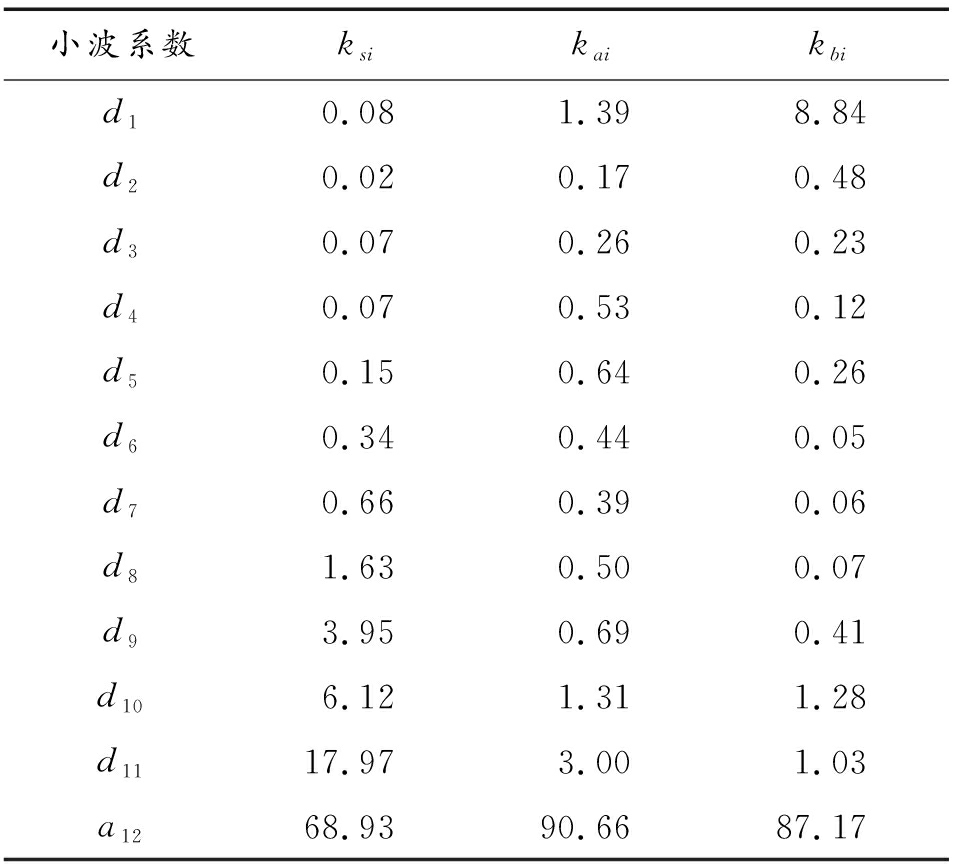
小波系数ksikaikbid10.081.398.84d20.020.170.48d30.070.260.23d40.070.530.12d50.150.640.26d60.340.440.05d70.660.390.06d81.630.500.07d93.950.690.41d106.121.311.28d1117.973.001.03a1268.9390.6687.17
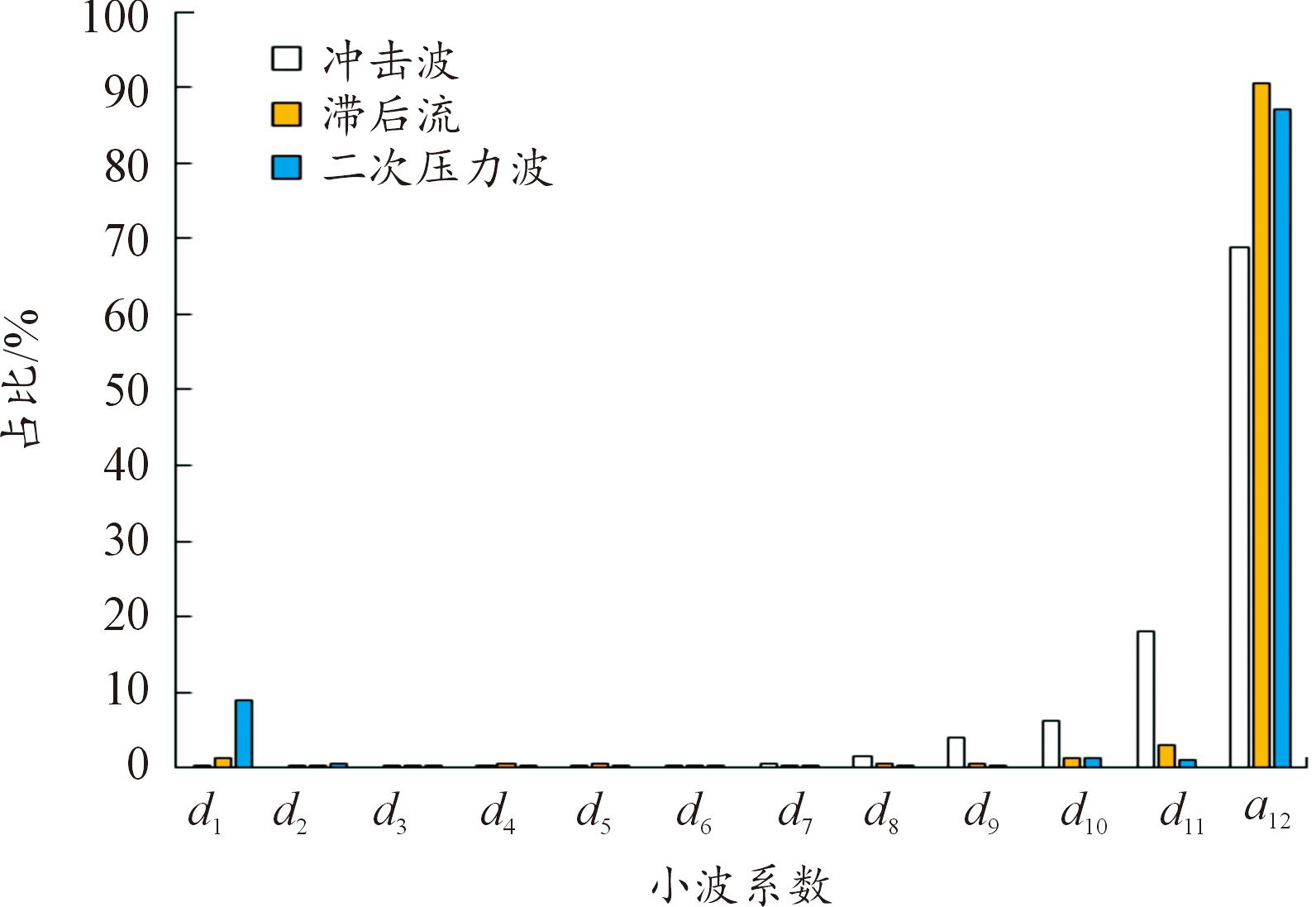
图6 各时段各频段能量占比
Fig.6 Energy ratio in each time period and frequency band
进一步分析水中沉底爆炸压力信号在各时段的能量分布,分别对小波重构压力信号的冲击波时段、滞后流时段和二次压力波时段的能量进行了计算,即以每个时段压力峰值时间的中点进行划分,冲击波压力和滞后流压力峰值时间的中点划分冲击波与滞后流,以冲击波和二次压力波峰值时间的中点划分为滞后流与二次压力波。图7为各时段能量占比。

图7 各时段能量占比
Fig.7 Energy ratio for each stage
3.3 结果分析
由表2和图5小波分解后计算各频段能量可知,大当量装药沉底爆炸后爆炸能量主要集中在低频段,其中0.244 kHz以下频段能量占总能量的76.6%,在3.906 kHz频段以下的能量占总能量的97.4%。对其他压力测点数据进行分析显示,3.906 kHz频段内的能量与总能量比值均大于95%。
由压力占比计算结果可知,0.244 kHz以下的频段对压力峰值影响最大,达到了39%以上,125 kHz以下频段压力占总峰值压力的98.85%;125 kHz以上频段能量和压力占比都很小,分解重构后的信号显示主要是噪声信号。与文献[2]中0.5 kg TNT装药水中爆炸的90%能量集中在8 kHz在以下相比,大当量装药水中爆炸能量占比大的频率段明显降低。
表3和图6的冲击波、滞后流和二次压力波3个时段分段小波分析结果显示,冲击波时段内3.906 kHz频段以下能量占总能量的98.43%、滞后流时段内该频段以下能量占总能量的96.18%、二次压力波时段内该频段以下的能量占二次压力波总能量的97.07%。说明在压力波的3个不同时段内,能量仍然是集中在4 kHz以下的低频段。
图7显示,冲击波时段、滞后流时段和二次压力波时段能量在总能量中占比分别为64.5%、29.9%、5.6%,说明装药沉底爆炸冲击波时段能量占比最大,滞后流时段次之,二次压力波时段能量很小。说明与自由场条件下爆炸相比二次压力波时段能量占比明显变小,沉底爆炸导致了能量分布变化。
4 结论
对大当量装药沉底爆炸条件下压力信号时频特征分析可以得到如下结论:
1) 采用小波分析方法分析水中爆炸压力信号,对信号进行多层细分,方法合理可行,能得到信号不同频段的时频特征。
2) 大当量装药水中沉底爆炸压力信号中,4 kHz以下频段能量超过了95%,250 Hz以下频段能量占比超过75%,250 Hz以下频段冲击波压力峰值占比达39%,说明与小当量装药爆炸相比,大当量装药沉底爆炸的能量分布向更低频段集中。
3) 冲击波时段能量达到64%,滞后流时段能量占30%,而二次压力波时段能量仅占6%,说明沉底爆炸导致了能量分布变化,与自由场条件下爆炸相比,气泡脉动收缩二次压力波时段能量占比明显变小,爆炸能量主要集中在冲击波和滞后流时段,说明气泡二次脉动载荷对目标毁伤发挥的作用变小。
4) 在沉底爆炸条件下舰艇结构和设备抗冲击响应分析时在频域应重点关注低频段影响,在时域应重点关注冲击波和滞后流时段的影响。
[1]李国华,李玉节,张效慈,等.气泡运动与舰船设备冲击振动关系的试验验证[J].船舶力学,2005,9(1):98-105.LI Guohua,LI Yujie,ZHANG Xiaoci,et al.Experimental verification of relationship between bubble motion and shock vibration of ship equipment[J].Journal of Ship Mechanics,2005,9(1):98-105.
[2]谢耀国,崔洪斌,李新飞,等.水下爆炸条件下自由场压力载荷时频特性分析[J].中国舰船研究,2016,11(2):27-32,50.XIE Yaoguo,CUI Hongbin,LI Xinfei,et al.Time-frequency characteristics analysis of free-field pressure with underwater explosion[J].Chinese Journal of Ship Research,2016,11(2):27-32,50.
[3]金辉,张庆明,郑长允.装药水下沉底爆炸压力场特性研究[J].科技导报2009,27(14):32-37.JIN Hui,ZHANG Qingming,ZHENG Changyun,et al.Characteristics of pressure field in ground explosion[J].Science & Technology Review,2009,27(14):32-37.
[4]李洪涛,赵琳,宁永成,等.球形装药海底裸爆压力测试与分析[J].工程爆破,2005(1):16-21.LI Hongtao,ZHAO Lin,NING Yongcheng,et al.Testing and analyzing pressure produced by submarine expolsion with spherical charges[J].Engineering Blasting,2005(1):16-21.
[5]ZAMYSHLYAYEV B V.Dynamic loading in underwater explosion,AD-757183[R].[S.l.]:[s.n.],1973.
[6]姚熊亮,杨文山,陈娟,等.沉底水雷爆炸威力的数值计算[J].爆炸与冲击,2011,31(2):173-178.YAO Xiongliang,YANG Wenshan,CHEN Juan,et al.Numerical calculation of explosion power of mines lying on seabed[J].Explosion and Shock Wave,2011,31(2):173-178.
[7]杨莉,汪玉,杜志鹏,等.沉底装药水下爆炸冲击波传播规律[J].兵工学报,2013,34(1):100-104.YANG Li,WANG Yu,DU Zhipeng,et al.Research on shock wave propagation of underwater explosion of bottom charge[J].Acta Armamentarii,2013,34(1):100-104.
[8]顾文彬,阳天海,叶序双,等.单个装药浅层水中沉底爆炸的数值模拟[J].解放军理工大学学报(自然科学版),2000,1(3):51-55.GU Wenbin,YANG Tianhai,YE Xushuang,et al.Numerical simulation of single charge explosion on seabed in shallow water[J].Journal of PLA University of Science and Technology(Natural Science Edition),2000,1(3):51-55.
[9]郅斌伟,张志江,马硕,等.水底爆炸冲击波峰值压力数值仿真[J].爆破,2011,26(1):22-28.ZHI Binwei,ZHANG Zhijiang,MA Shuo,et al.Research on shock wave peak pressure of under water explosion[J].Blasting, 2011,26(1):22-28.
[10]金辉,李兵,权琳,等.不同边界条件下炸药水中爆炸的能量输出结构[J].爆炸与冲击,2013,33(3):325-328.JIN Hui,LI Bing,QUAN Lin,et al.Configuration of explosive energy output in different underwater boundary conditions[J].Explosion and Shock waves,2013,33(3):325-328.
[11]邵建军,张永坤,赵红光,等.基于相似理论的炸药海中沉底爆炸能量计算[J].四川兵工学报,2015,36(6):175-180.SHAO Jianjun,ZHANG Yongkun,ZHAO Hongguang,et al.Energy calculation of underwater explosion over seabed charge based on similarity law[J].Journal of Sichuan Ordnance Engineering,2015,36(6):175-180.
[12]张姝红,金辉.大当量集团装药水中沉底爆炸特性试验研究[J].舰船电子工程,2023,347(5):199-202.ZHANG Shuhong,JIN Hui.Test research on underwater bottom explosion characteristic of large equivalent group charge[J].Ship Electronic Engineering,2023,347(5):199-202.
[13]温华兵,张健,尹群,等.基于小波变换的水下爆炸压力时频特征分析[J].振动、测试与诊断,2008,28(6):199-203.WEN Huabing,ZHANG Jian,YIN Qun.Time-frequency characteristic analysis of underwater explosion pressure based on wavelet transform[J].Journal of Vibration,Measurement &Diagnosis,2008,28(6):199-203.
[14]宋敬利,贾则,赵琳,等.基于小波变换的缓冲平台隔振性能分析[J].海洋技术,2009,2(6):65-68.SONG Jingli,JIA Ze,ZHAO Lin,et al.Vibration isolation performance analysis of buffer platform based on wavelet transform[J].Ocean Technology,2009,2(6):65-68.
[15]谢宇超,周海滨,陶妍.基于小波分解的水中电爆炸冲击波波形重建方法研究[J].振动与冲击,2021,40(5):149-153.XIE Yuchao,ZHOU Haibin,TAO Yan.Reconstruction method of shock wave shape of underwater electric explosion based on wavelet decomposition[J].Journal of Vibration and Shock,2021,40(5):149-153.