0 引言
随着国家航天事业的快速发展和空间站的建成,航天器上含有大量使用轻质复合材料制作的柔性化和低刚度的悬臂梁结构构件。但太空环境恶劣复杂多变,真空环境阻尼小、振动难易快速衰减,容易造成悬臂结构件的振动,这将影响航天器的正常工作,因此必须采取有效措施进行悬臂结构件的振动控制。
压电材料作为一种智能材料,具有良好的机电耦合特性,在振动控制领域有着良好的应用。基于压电材料的压电振动控制有主动、被动和半主动3种方法[1-2]。与主动、被动控制相比,半主动振动不需要精准的结构振动模型,控制系统简单,控制所需要的外界能量小,就能实现比较稳定的控制效果,受到相关研究者的推崇。
结合压电陶瓷将航天器上使用的某种轻质复合材料制作成智能悬臂梁结构件进行振动控制研究,以期为航天器上的柔性和低刚度悬臂结构件的振动控制探索有效可行的方法。
采用有限元法对悬臂梁结构件建模求得其振动状态方程,通过试验法测量梁的振动固有特性参数,为振动控制系统的设计提供模型参数。
状态观测器可以获得精确、无时延的振动模态而且还可以进行模态相互分离,实现对不同的振动模态进行独立控制,因此引入状态观测器用于获取智能悬臂梁结构的各阶振动模态,为半主动控制提供开关切换信号和控制参数。
为了增强系统控制的鲁棒性,设计自适应SSDV控制技术,根据实际振动状况动态调整控制参数,使控制效果始终朝最佳状态优化。
1 智能悬臂梁结构模型的建立
智能悬臂梁结构模型如图1所示。压电陶瓷片(PZT)粘接于悬臂梁根部。利用有限元法对其进行结构建模[3-9],得到结构的动态运动方程为
![]()
(1)
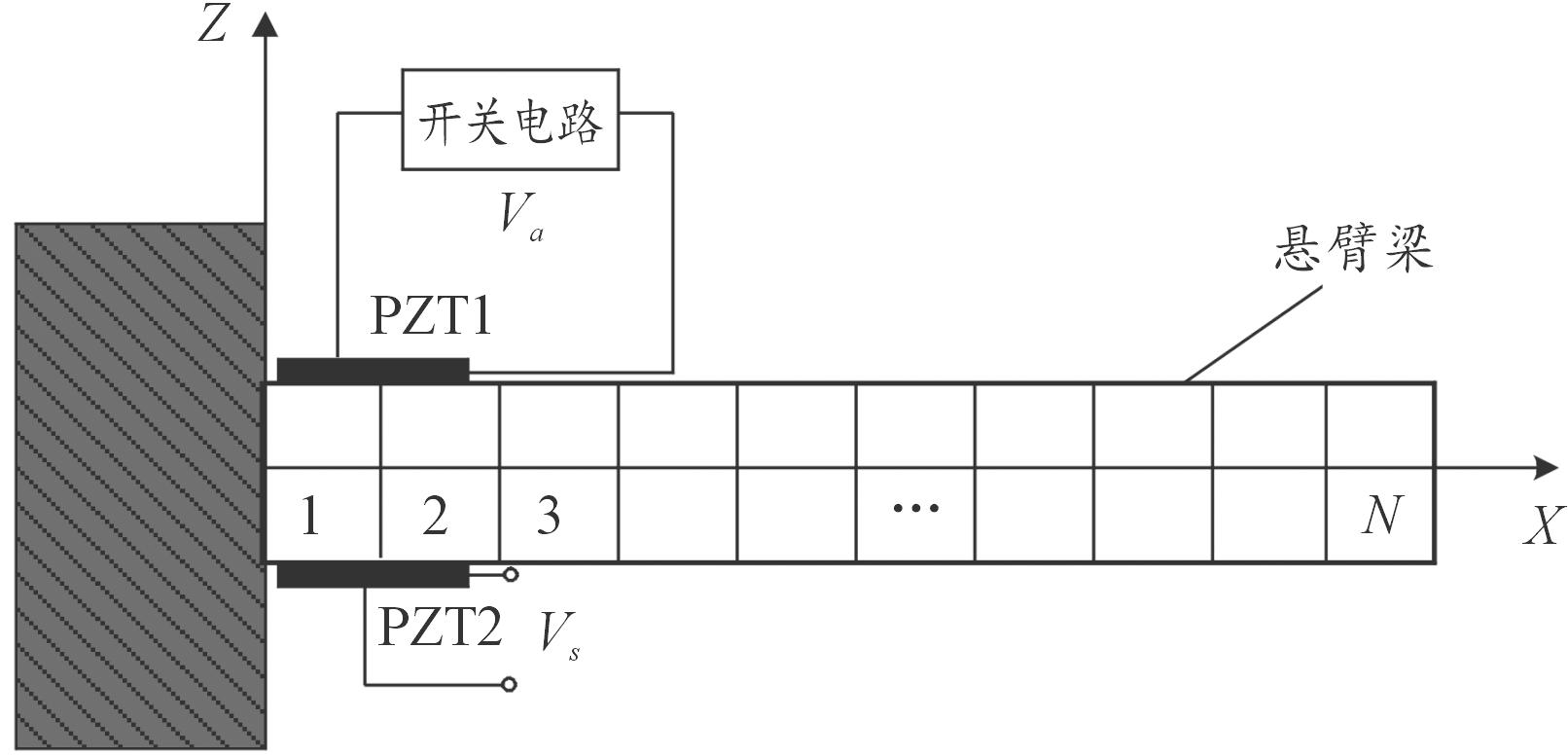
图1 智能悬臂梁结构模型
Fig.1 Intelligent cantilever beam structure model
式(1)中: δ为梁振动位移向量;m、c、kE分别为梁的质量、阻尼和刚度矩阵;α为机电耦合矩阵;V为压电陶瓷片(压电片)上的电压向量。
压电片闭合时电路中的电流向量为
![]()
(2)
式(2)中,C0为压电片等效电容矩阵。
由振动理论的展开定理,对式(1)中的物理坐标进行模态坐标转换:
δ=φq
(3)
式(3)中: q为梁的模态位移向量; φ为梁的模态振型矩阵。
在模态坐标下,式(1)和式(2)可写成:
![]()
(4)
式(4)中: M、C、KE分别为梁的模态质量、模态阻尼和模态刚度矩阵; θ为模态机电耦合矩阵。
θ=φTα
(5)
假设悬臂梁的模态个数为L,有限元分析中的节点个数为N,结构上粘贴的压电片个数为n,则矩阵θ的维数为[L,n],φ为[N,L],α为[N,n],θ只与结构的模态有关。
埋入的2片压电片的电压V分别为控制电压Va和传感电压Vs,则式(4)可以改写成:
![]()
(6)
对于传感压电片而言,压电片的外接电路相当于开路,所以电路中的电流为零,则由式(2)和式(5)可得:
![]()
(7)
再将式(7)代入式(6)可得:
![]()
(8)
由式(7)和式(8)可得系统的状态方程:
![]()
(9)
其中,x为状态向量,u为控制向量,y为输出向量,系统中u=Va,y=Vs。A、B、G均为状态矩阵。表达式如下:
![]()
(10)
状态方程中的各参数利用试验方法来测量,因此将系统的模态质量矩阵M进行归一化处理:
M=φTmφ=I
(11)
将埋入结构中的2片压电片的两端均短接,则式(6)可以写成:
![]()
(12)
梁结构可以看作是无模态耦合的柔性结构,所以模态阻尼矩阵和模态刚度矩阵可以写成:
C=diag(2×2πξfc)
(13)
KE=diag((2πξfc)2)
(14)
其中: fc为压电片都短路时的结构固有频率向量,ξ为梁的阻尼比。用于传感的压电片,其外电路可看作开路;用于控制的压电片,其外电路可看作短路。则式(8)可改写成:
![]()
(15)
由式(14)可得:
![]()
(16)
其中, fco为一片压电片开路,另一压电片短路时的结构固有频率向量。将式(14)代入式(16)可得开路压电片的模态机电耦合矩阵为
![]()
(17)
重复上述过程,将原开路的压电片短路,原短路的压电片断开,则求得的θ0即为另一压电片的模态机电耦合矩阵。
试验装置如图2所示,梁的材料为轻质复合材料[10],尺寸为180 mm×50 mm×0.5 mm,压电片的尺寸为30 mm×30 mm×0.2 mm。在梁的自由端安装激光位移传感器(KEYENCE-LK080),用于测量悬臂梁自由端的振动位移信号,信号由dSPACE的AD口采集。

图2 试验装置
Fig.2 Testing apparatus
式(8)—式(10)中所需参数的试验测量值如表1所示。
表1 悬臂梁的固有特性参数
Table 1 Inherently characteristic parameters of cantilever beam

参数名称振动模态i=1i=2控制电路短路时梁的模态频率fi0/Hz20.02107.3控制电路开路时梁的模态频率fi1/Hz20.05107.4控制电路开路时压电片电压与自由端位移比λi/(V·m-1)973.9227.3压电片等效电容C0/nF65.5965.59控制电路开路时梁的阻尼比ξi0.009 60.015 3
2 状态观测器的设计
要实现结构的减振降噪必须要获取其主要振动模态,因结构的振动能量主要集中在前几阶振动模态中,故本研究主要研究前两阶振动模态的控制。
对于结构的振动模态识别,常采用线性相位FIR数字滤波器对采集的时域信号进行滤波处理以获得结构振动的主要模态。此方法虽然可以有效抑制噪声或者其他模态的影响,但是滤波器的使用会不可避免地带来相位延时的问题,这将影响开关信号的控制,从而减弱控制效果。因此,如何获得精确、无时延的主要振动模态对于结构的减振降噪至关重要。
为了消除数字滤波器在模态识别中的缺陷,本研究引入状态观测器[11-14]到振动控制中,构造一个与实际控制系统具有相同属性的观测系统,利用实际控制系统中可直接测量的输入和输出作为状态观测器的输入,再用观测的状态变量(如模态位移或模态速度)作为生成开关控制信号的输入信号,就可以准确地判断控制对象模态位移的极值位置,以此消除测量噪声以及其他模态引起的频繁切换。另外,该方法还可以进行模态相互分离,因此可以实现对不同的振动模态进行独立控制,这是多模态半主动控制的重要方法之一。
由振动控制理论可知,通过引入积分环节可消除系统稳态误差可提高系统控制的稳态精度[15]。因此本研究设计的状态观测器在全维观测器的基础上引入实际系统输出与观测器系统输出误差e的积分,即PI观测器,如图3所示。
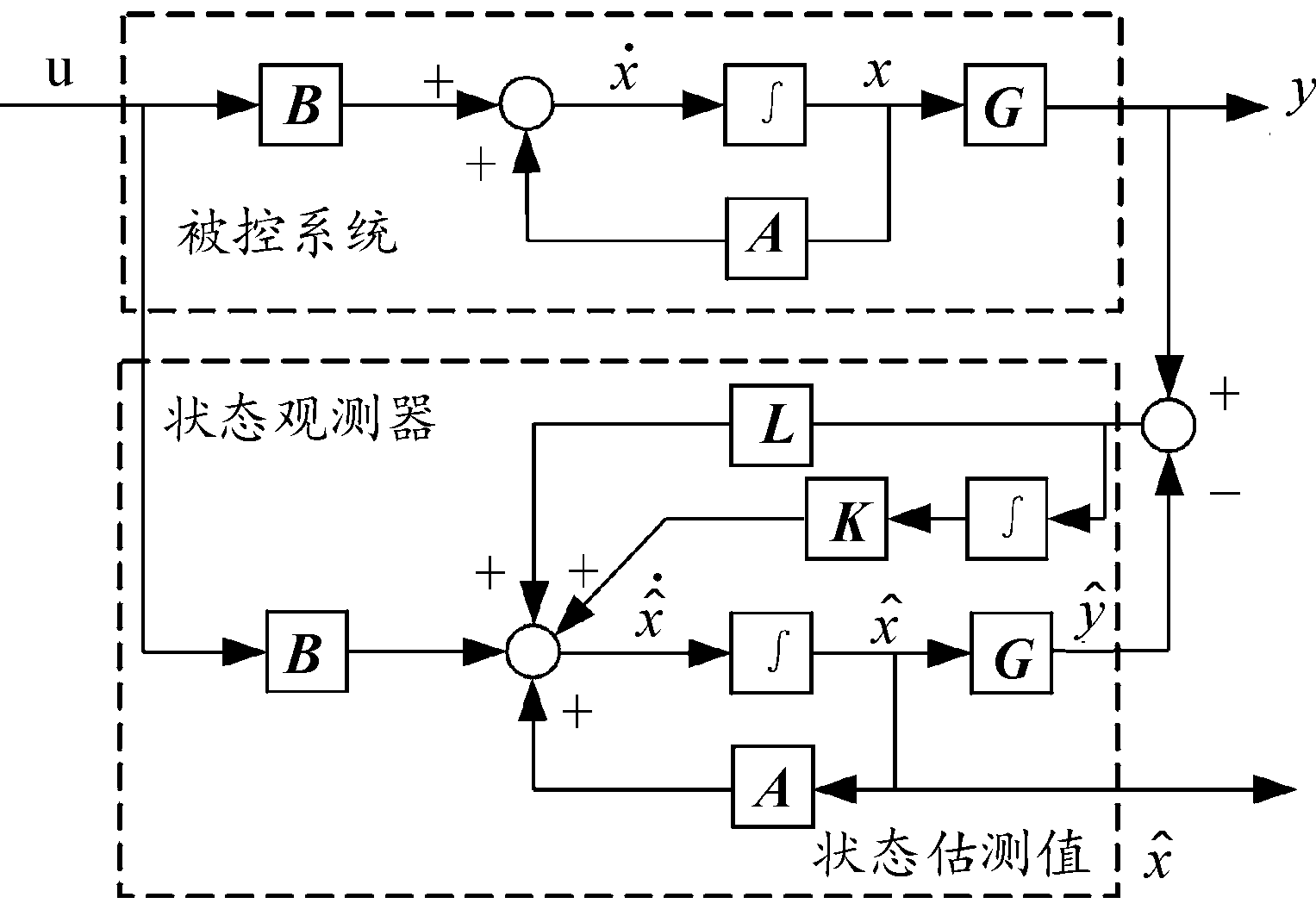
图3 PI观测器工作原理图
Fig.3 PI observer operating schematic
根据已建立的智能悬臂梁结构模型,设计的PI观测器如下:
![]()
(18)
![]() 为状态估计向量;ω∈Rp为加权输出估计误差的积分;L∈Rn×m、F∈Rn×p、K∈Rp×m分别为比例增益矩阵,积分增益矩阵和输出误差权矩阵。根据结构模型对观测器的3个参数L、F、K进行求解。
为状态估计向量;ω∈Rp为加权输出估计误差的积分;L∈Rn×m、F∈Rn×p、K∈Rp×m分别为比例增益矩阵,积分增益矩阵和输出误差权矩阵。根据结构模型对观测器的3个参数L、F、K进行求解。
对观测器的要求是,对于任意输入u(t)和任意初值![]() 满足下述关系:
满足下述关系:
![]()
(19)
![]()
(20)
其中
![]()
(21)
由式(7)、式(18)和式(21)可得下式:
![]()
(22)
其中,![]()
要使观测器满足要求,则要求式(22)必须有解,寻求(L,F,K)使得A0稳定并且是非退化的。
设A0的左特征向量矩阵为![]() 于是
于是![]() 由定义可得:
由定义可得:
![]()
(23)
其中, Λ=diag(s1,s2,…,sn+p),且{s1,s2,…,sn+p}是自共轭的。
则式(23)可等效为
![]()
(24)
令:
-ZT=TTL+VTK
(25)
则式(24)的上式可以转化为TTA+ZTG=ΛTT,为Sylvester矩阵方程的对偶形式,可进行如下的右互质分解:
(sI-AT)-1GT=N(s)D-1(s)
(26)
则矩阵T、V、Z的参数表达式为
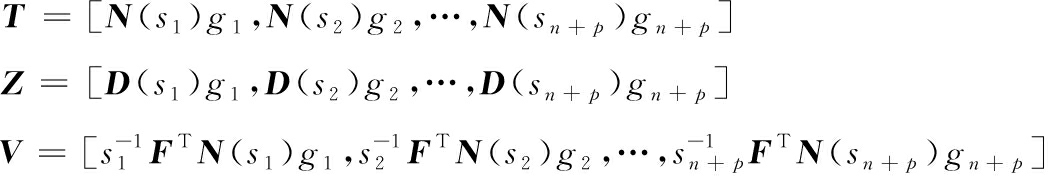
(27)
将式(27)代入式(25),得矩阵L、K的解为
![]()
(28)
通过试验,得到智能悬臂梁的前两阶振动模态的观测参数为:
一阶振动模态观测参数:

二阶振动模态观测参数:

3 自适应SSDV控制技术
结构的振动模态识别后,就可以根据识别的模态参数对其进行压电半主动振动控制。本研究采用的同步开关阻尼(synchronized switch damping,SSD)技术[16-17]是一种基于压电智能结构的半主动控制技术,控制电路如图4所示。

图4 同步开关阻尼振动控制技术及压电片位移、电压图
Fig.4 SSD vibration control technology and piezoelectric plate displacement,voltage diagram
其中开关电路1为基于电感的同步开关阻尼技术(SSDI)。其控制技术的原理是,当开关闭合,控制电路将发生LC谐振,使压电片上产生一定的附加力,其方向与结构的振动速度方向始终相反,从而实现振动控制。控制的过程是,当结构振动位移u达到最值(uM或-uM)时压电片上的电压V也达到极值(VM或-VM),此时开关SW立即闭合,LC振荡器发生谐振,半个周期后压电片上的电压发生翻转,由正电压VM变成负电压-Vm(或由负电压-VM变成正电压Vm)时,立即断开开关,之后压电片由于振动继续发生形变至最大值,到达新的控制周期再闭合开关。在SSDI电路中,通过周期性地控制开关的闭合与断开,实现结构的半主动振动控制。
开关电路2为基于电压的同步开关阻尼技术(SSDV)。SSDV控制技术原理与SSDI相似,也是在压电片上的电压幅值达到峰值时闭合控制开关并保持半个LC谐振周期至压电片电压翻转。不同的是,SSDV是在SSDI电路基础上串联附加电源Vcc,附加电源的电势与控制开关闭合时压电片上的电势相反,故需安排一组电压值相等但电势相反的附加电源。由于附加电源提高了压电片翻转时电压幅值,其作用相当于增大了系统的阻尼,这对于抑制振动是有利的。
经典SSDV控制技术的附加电源Vcc值的大小是固定不变的,像是一种开环控制,对于固定激励的振动可以实现较好的控制,但随机状况下振动控制效果就难以得到保障。因此为了增强振动控制的鲁棒性,必须根据结构振幅的大小而随之动态正比调整附加电源Vcc的大小以适应实际状况。这就需要将经典SSDV控制技术设计成自适应SSDV控制技术,自适应SSDV像是一种闭环控制,带有反馈控制系统,促使控制效果始终朝着最佳优化。自适应SSDV技术的控制电路如图5所示。

图5 自适应SSDV技术控制原理
Fig.5 Adaptive SSDV technology control principle
Vcc的值根据以下方式进行调整:
![]() 当应变达到最大值时
当应变达到最大值时
![]() 当应变达到最小值时
当应变达到最小值时
但是如何选择合适的电压系数β,使控制效果始终保持优,这非常重要。因为如果系数β选择过大,会引起控制不稳定,如果系数β选择过小,控制效果不明显。通常需要根据试验条件和经验,手动设定或调节β的大小。对于每个恒定的系统,都有一个优的值。但是当系统发生变化,例如受到噪声的影响等,此时优的值将发生变化,需要重新优化。因此为了适应实际状况,电压系数β必须进行在线实时优化,使得结构振动越来越小,并且始终保持优。
本研究采用LMS算法[18-19]进行电压系数β的自适应调整。LMS是适合自适应滤波的标准算法,计算复杂程度适中、收敛性好,在工程中应用广泛,能够根据结构的实际振动状况自动优化参数,使得期望误差越来越小。电压系数β不是每一离散时间都进行计算更新,只在开关切换点才进行优化。因此,本研究用结构振动位移极值uM而不用位移u来作为误差信号输入到状态观测器中。状态观测器在开关切换点处输出电压系数以此计算附加电压源幅值,直到下一个开关切换时才更新。
4 试验结果与讨论
4.1 多模态激励下梁的振动控制试验
根据前述试验实际测得的悬臂梁前两阶固有振动模态特征参数,进行多模态激励下悬臂梁的振动控制试验,2个频率的幅值按1∶2设置。设计的PI状态观测器可以对2个振动模态进行独立观测,图6和图7分别为悬臂梁前二阶振动模态自由端位移值波形及观测器观测值波形的对比。
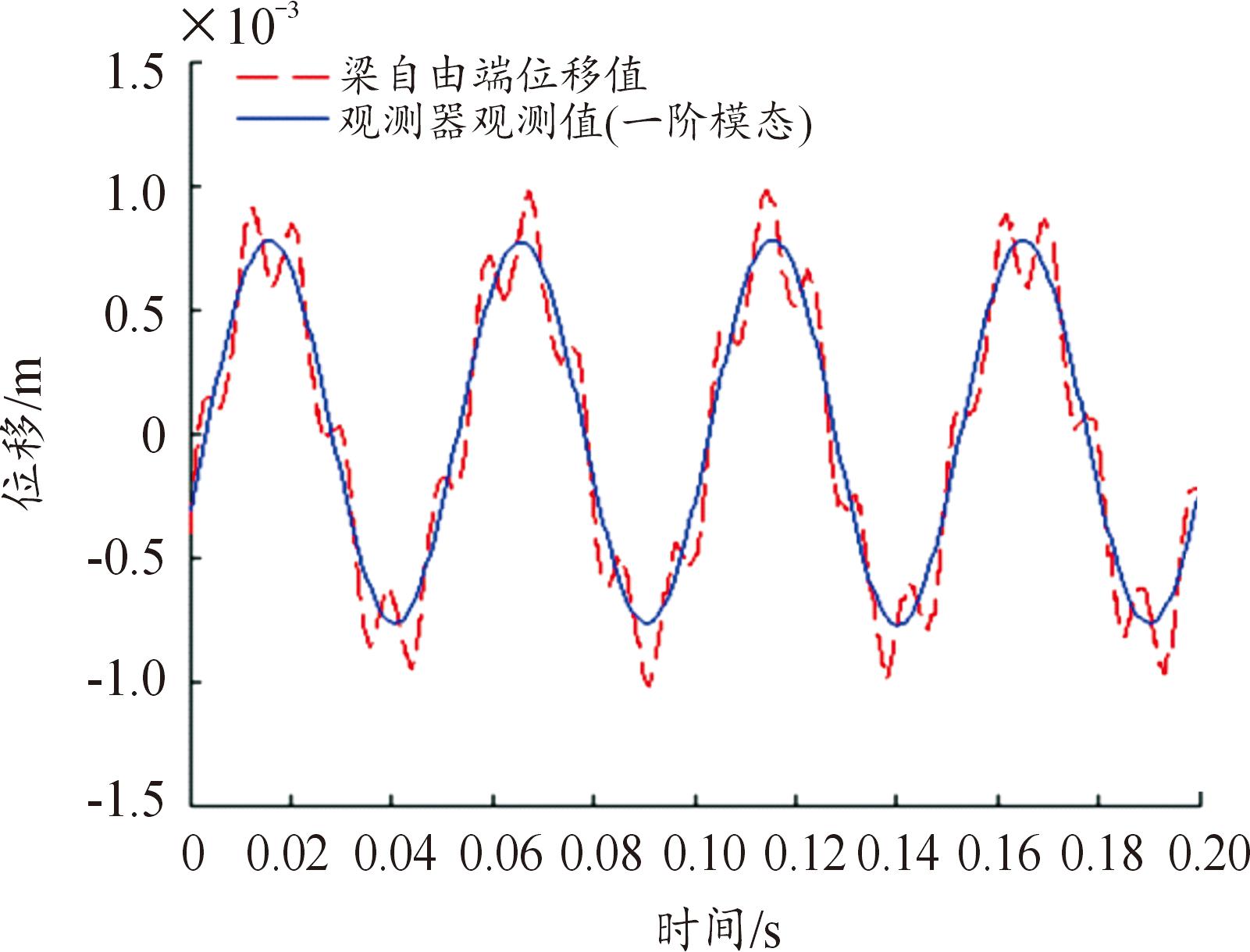
图6 一阶振动模态下梁自由端位移及其观测值
Fig.6 The displacement of the free end of the beam in the first-order vibration mode and its observations
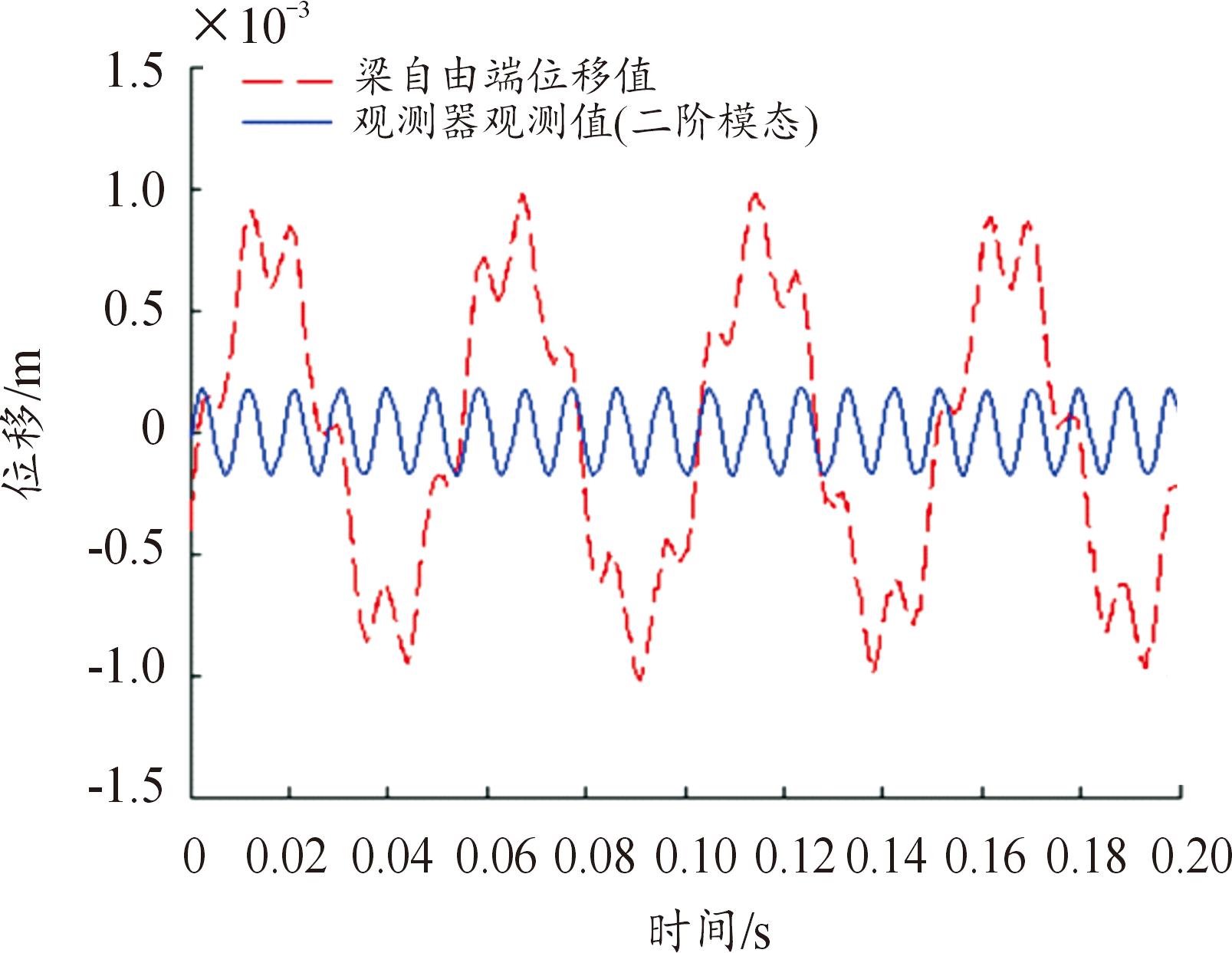
图7 二阶振动模态下梁自由端位移及其观测值
Fig.7 The displacement of the free end of the beam in the second-order vibration mode and its observations
图8为悬臂梁自由端振动位移波形和整体观测波形的多周期采集,可以看出梁自由端位移值及其整体观测值吻合度高。图9是图8中两者的FFT分析比较,可以看出悬臂梁前两阶振动模态的实际测量值与状态观测器观测值的误差分别仅为0.44 dB(0.68%)和0.67 dB(0.9%)。这表明本研究设计的状态观测器具有较好的观测效果。
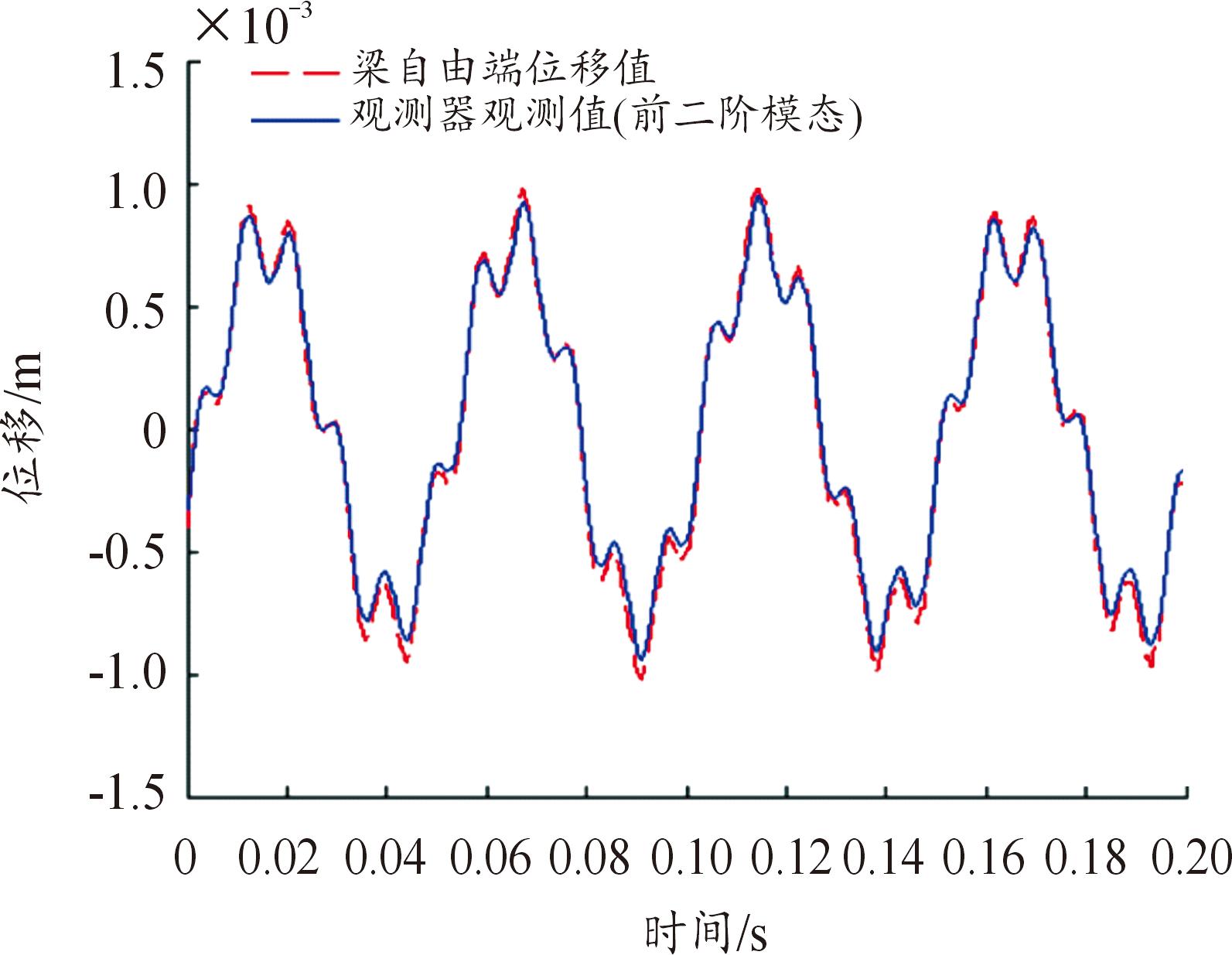
图8 梁自由端位移及其整体观测值
Fig.8 The displacement of the free end of the beam and its overall observations
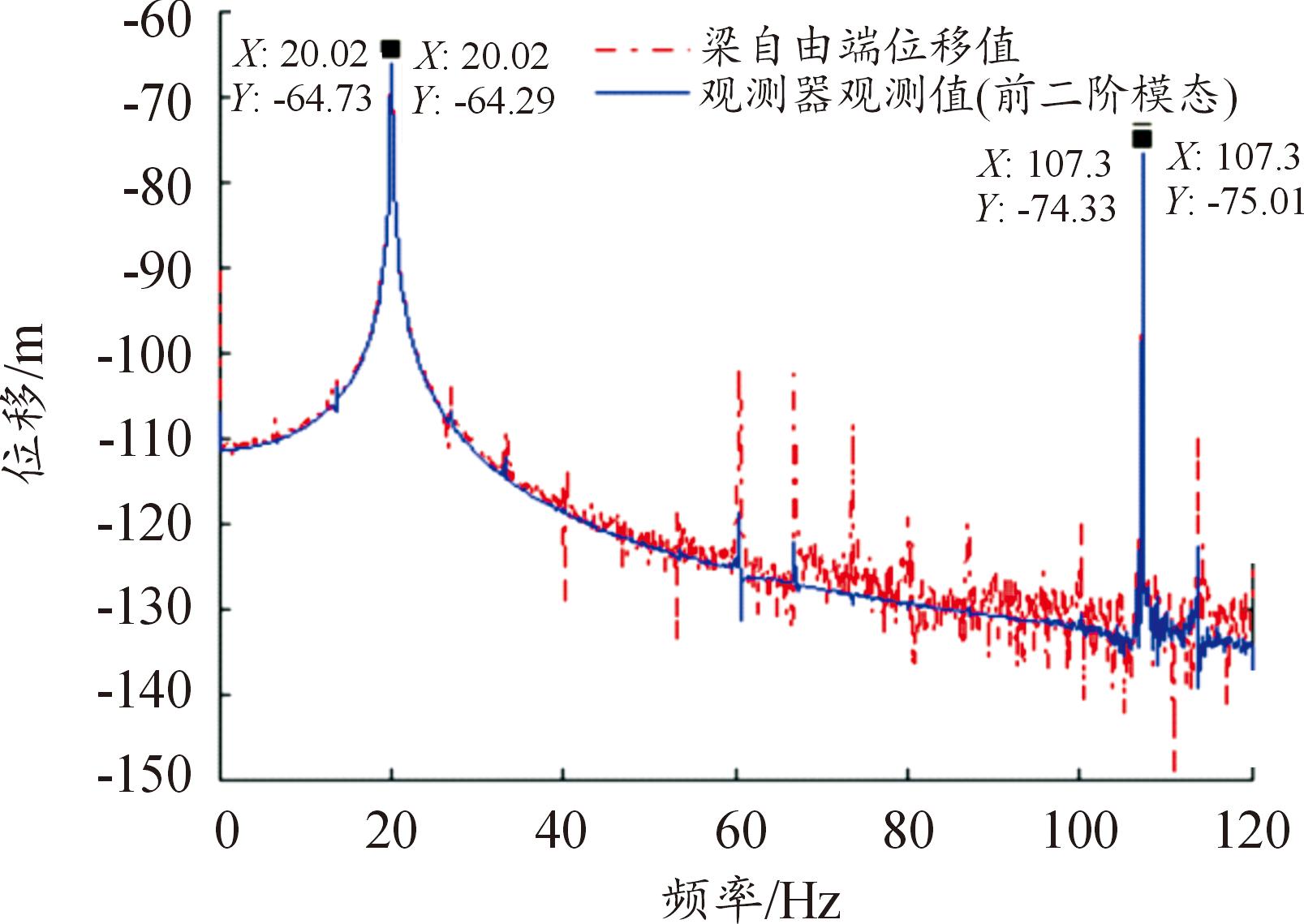
图9 梁自由端位移及其观测值的FFT分析比较
Fig.9 Comparison of FFT analysis of beam free end displacement and its observations
对悬臂梁的一阶振动模态进行自适应SSDV控制后,同步采集多个周期的梁自由端位移值、状态观测器观测值和压电片电压值进行比对,如图10所示,可以看出悬臂梁的一阶振动得到稳定控制。

图10 控制后梁自由端位移、观测值和压电片电压值
Fig.10 Beam free end displacement,observations,and piezoelectric voltage values after control
悬臂梁的一阶振动模态下,将未采用控制和采用自适应SSDV控制的自由端位移信号进行FFT分析,其结果如图11和表2所示。
表2 悬臂梁一阶振动模态进行自适应SSDV控制前后的效果比较
Table 2 Comparison of the effect of the first-order vibration mode of the cantilever beam before and after adaptive SSDV control
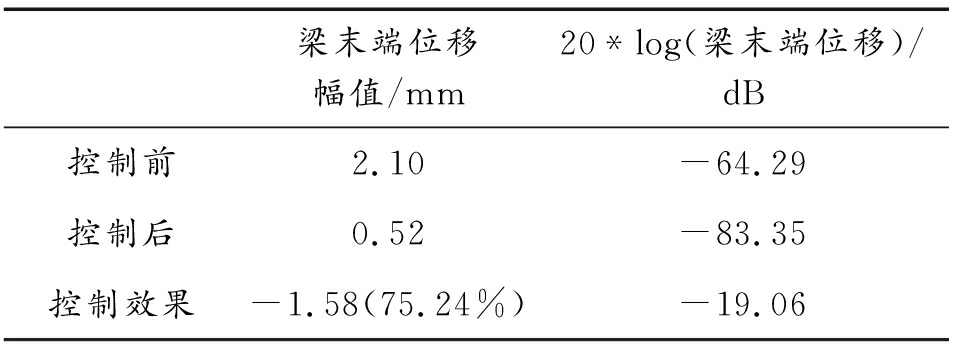
梁末端位移幅值/mm20*log(梁末端位移)/dB控制前2.10-64.29控制后0.52-83.35控制效果-1.58(75.24%)-19.06

图11 控制前后梁自由端位移的FFT分析比较
Fig.11 Comparison of FFT analysis of beam free end displacement before and after control
由表2可以看出,自适应SSDV控制技术对悬臂梁的多模态振动控制产生较好的效果,一阶振动幅值降低了75.24%。
4.2 随机信号激励下梁的振动控制试验
在实际中,引起结构振动的信号源大多为随机信号,因此有必要检验悬臂梁在随机信号激励下的振动控制效果。
在随机信号激励下,悬臂梁自由端的位移值及其观测值的对比如图12所示。两者的FFT分析对比如图13所示。

图12 梁自由端位移及其观测值
Fig.12 Beam free end displacementand its observations

图13 梁自由端位移及其观测值的FFT分析比较
Fig.13 Comparison of FFT analysis of beam free end displacement and its observations
可以看出在20.02 Hz处两者的纵坐标数值非常接近(仅相差0.22 dB),体现本研究设计的状态观测器有较好的模态识别精确度。
由图13看出,随机信号的引起的振动能量主要集中在第一阶模态,因此本文研究随机信号激励下悬臂梁的一阶振动的自适应SSDV控制。图14为同步采集多个周期悬臂梁自由端位移、状态观测器观测值和压电片电压值的比对,图15是图14的局部放大。可见随机信号激励下悬臂梁的一阶振动也得到稳定控制。

图14 控制后梁自由端位移、观测值和压电片电压值
Fig.14 Beam free end displacement,observations,and piezoelectric voltage values after control

图15 图14(0.6~1.2 s)的局部放大图
Fig.15 Local magnification of Fig.14
为了验证自适应SSDV控制技术对随机信号激励下悬臂梁的振动控制效果,采集控制前后的悬臂梁自由端位移信号(时长为30 s)进行FFT频谱分析,经平滑处理后对比结果如图16所示。其中图17是图16的局部放大。由图17可以看出,自适应SSDV控制技术对随机信号激励下的悬臂梁振动也具有较好的控制效果,一阶振动的能量下降10.81 dB。
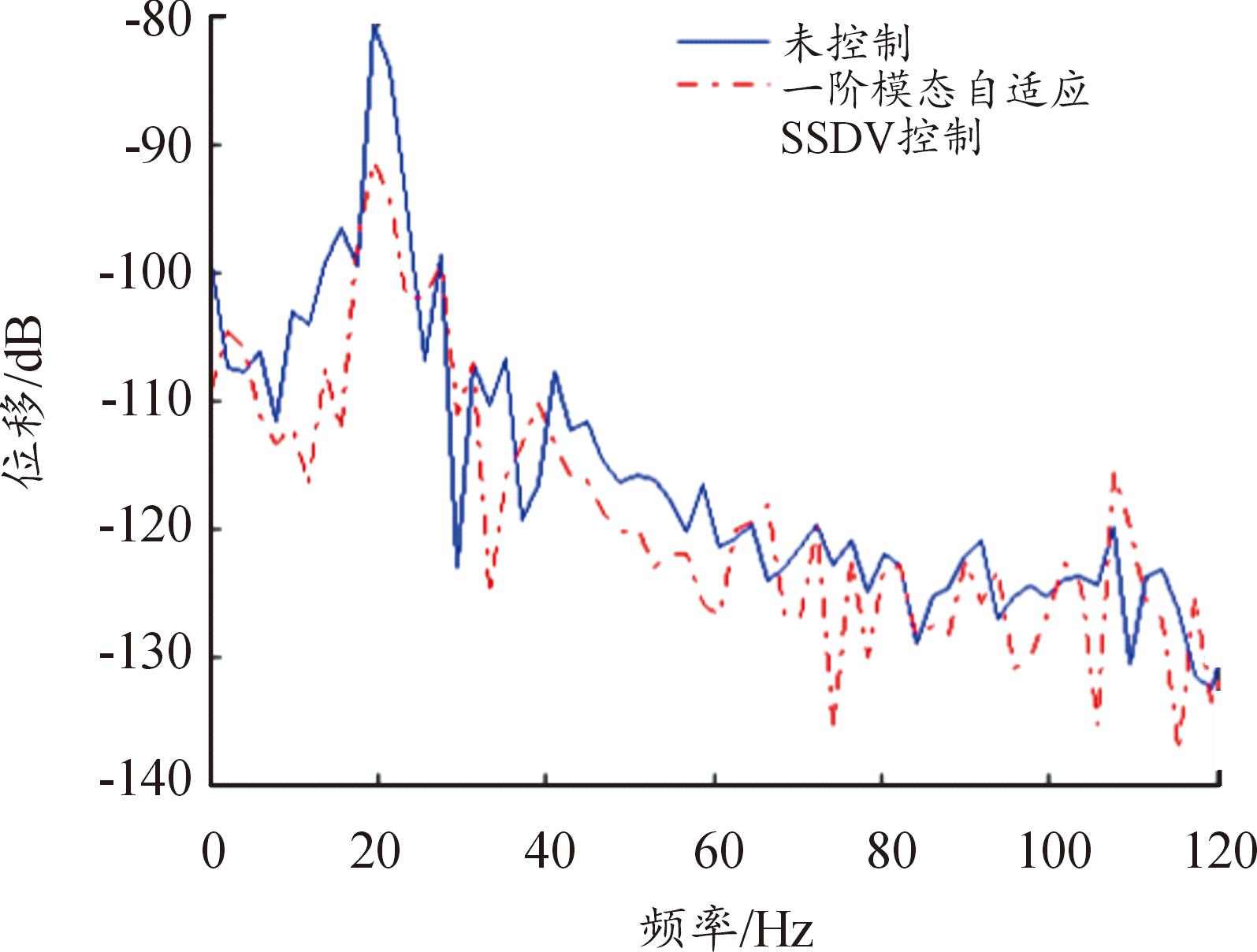
图16 随机信号激励下控制前后梁自由端位移的FFT分析比较
Fig.16 Comparison of FFT analysis of beam free end displacement under random excitationbefore and after control
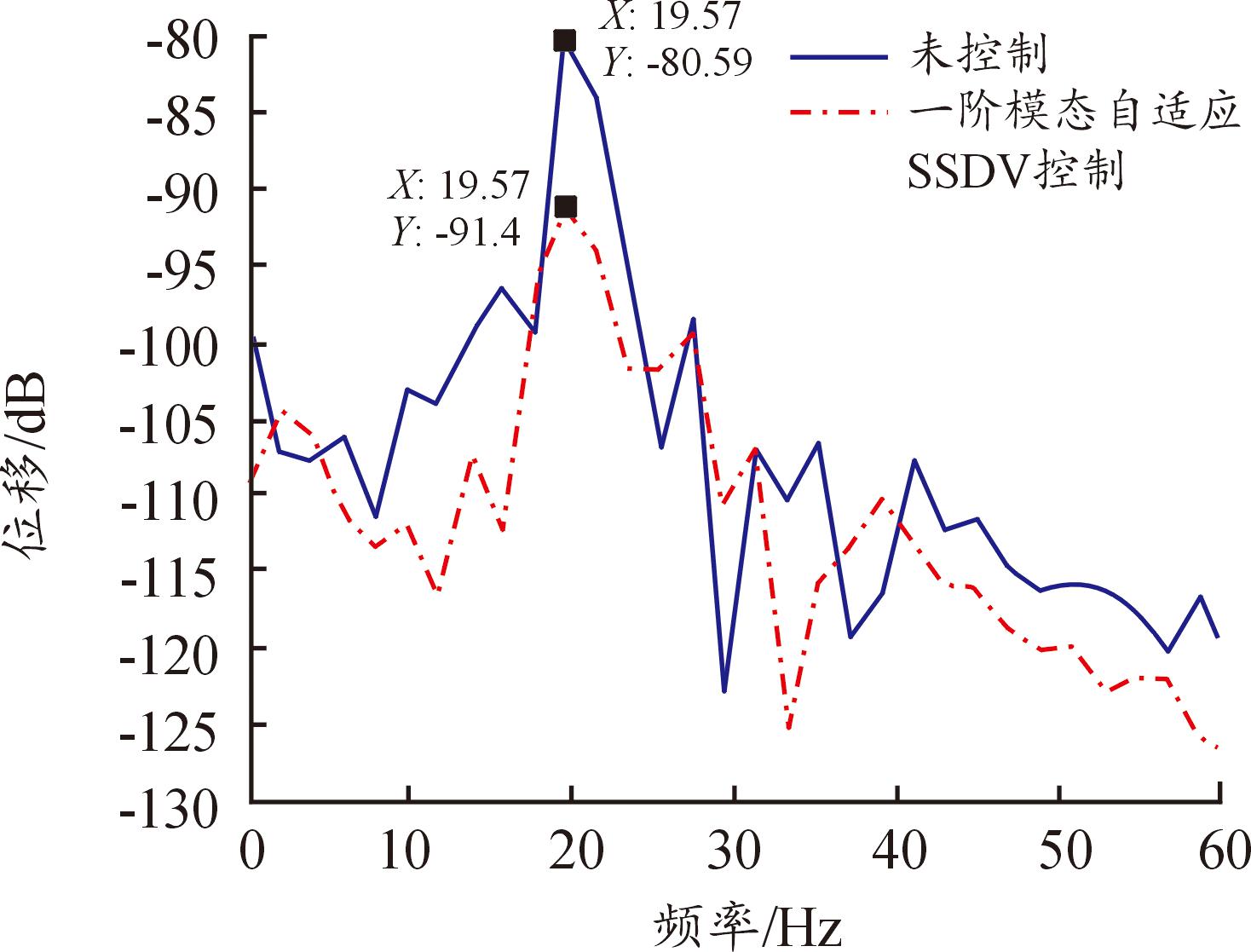
图17 图16的局部放大图
Fig.17 Local magnification of Fig.16
5 结论
以某种轻质复合材料制作的智能悬臂梁为载体进行基于状态观测器的自适应SSDV半主动振动控制研究。
1) 对智能悬臂梁进行有限元建模并设计了一种PI状态观测器用于振动模态的识别,试验证明设计的状态观测器具有良好的观测精度和模态识别精度,观测器观测值误差在1%之内。
2) 采用基于状态观测器的自适应SSDV控制技术对悬臂梁进行多模态振动控制试验,取得了良好的控制效果,试验条件下第一阶振动幅值减少了75.24%。同时,基于状态观测器的自适应SSDV控制技术对随机信号激励下的悬臂梁振动控制也具有较好的效果。
本研究为柔性化和低刚度的悬臂梁结构的振动控制提供一种有效可行的借鉴方法。
[1]杨云,曹亭.基于压电材料振动半主动控制仿真研究[J].计算机仿真,2020,37(2):263-268,376.YANG Yun,CAO Ting.Simulation research on semi-active controlof vibration based on piezoelectric materials[J].Computer Simulation,2020,37(2):263-268,376.
[2]顾仲权,马扣根,陈卫东.振动主动控制[M].北京:国防工业出版社,1997.GU Zhongquan, MA Kougen, CHEN Weidong.Active vibration control[M].Beijing: National Defense Industry Press,1997.
[3]刘宏梅,曹艳丽,陈克.机械结构有限元分析及强度设计[M].北京:北京理工大学出版社, 2018.LIU Hongmei, CAO Yanli, CHEN Ke.Finite element analysis and strength design of mechanical structure[M].BeiJing: BeiJing Institute of Technology Press,2018.
[4]戴宏亮,周加喜.工程有限元及数值计算[M].武汉:华中科技大学出版社,2019.DAI Hongliang, ZHOU Jiaxi.Engineering finite element and numerical calculation[M].Wuhan: Huazhong University of Science &Technology Press,2019.
[5]唐纪晔,黄海,夏人伟.压电复合材料层合板自适应结构的振动控制[J].计算力学学报,2000,17(4):441-446.TANG Jiye, HUANG Hai, XIA Renwei.Vibration control of adaptive structure using composite laminated piezoelectric element[J].Chinese Journal of Computational Mechanics,2000,17(4):441-446.
[6]钱振东,沈建华,黄卫,等.采用压电陶瓷元件进行智能板振动控制[J].振动、测试与诊断,2000,20(3):196-201,226.QIAN Zhendong, SHEN Jianhua, HUANG Wei, et al.Vibration control of smart plate using piezoelectric ceramic units[J].Journal of Vibration,Measurtment & Diagnosis,2000,20(3):196-201,226.
[7]亢佳佳.压电复合材料层合板自适应结构有限元分析及控制[D].西安:西安电子科技大学,2010.KANG Jiajia.Finite element analysis and control of adaptive piezoelectric laminates[D].Xi’an: Xidian University,2010.
[8]HARARI S, RICHARD C, GAUDILLER L, et al.New semi-active multi-modal vibration control using piezoceramic components[J].Journal of Intelligent Material Systems and Structures,2009,20:1604-1605.
[9]LEFEUVRE E, GUYOMAR D, PETIT L, et al.Semi-passive structure damping by synchronized switching on voltage sources[J].J.Intell.Mater.Syst.Struct,2006,17(8/9):653-660.
[10]QIU Jinhao, MASAKAZU H.Vibration control of a plate using a self-sensing piezoelectric actuator and an adaptive control approach[J].Journal of Intelligent Material Systems and Structures, 2006, 17(8/9):661-669.
[11]蔡亮亮.基于观测器的半主动多模态振动控制研究[D].南京:南京航空航天大学,2010.CAI Liangliang.A study on semi-active multi-modal vibration damping based on state-observer[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010.
[12]李中望.基于状态观测器的电镀液温度状态反馈控制系统[J].电镀与涂饰, 2021, 40 (4): 269-273.LI Zhongwang.State feedback control system for electroplating bath temperature based on state observer[J].Electroplating &Finishing, 2021, 40 (4): 269-273.
[13]章沪淦,卜仁祥,李宗宣.带状态观测器的船舶路径跟踪预测滑模控制[J].计算机仿真, 2021, 38 (9): 262-266,271.ZHANG Hugan,BU Renxiang,LI Zongxuan.Path following of ships based on predictive sliding mode control with state observer[J].Computer Simulation,2021, 38 (9): 262-266,271.
[14]胡寿松.自动控制原理[M].北京:科学出版社,2001.HU Shousong.Principle of automatic control[M].Beijing: Science Press,2001.
[15]段广仁.线性系统理论[M].哈尔滨:哈尔滨工业大学出版社,2004.DUAN Guangren.Linear system theory[M].Harbin: Harbin Institute of Technology Press,2004.
[16]RICHARD C, GUYOMAR D, AUDIGIER D, et al.Semi-passive damping using continuous switching of apiezoelectric device[C]// Proceedings of SPIE Smart Structures and Materials Conference.San Diego, CA 1999, 3672: 104-113.
[17]季宏丽,裘进浩,赵金玲.结构半主动振动控制-压电同步开关阻尼技术[M].北京:科学出版社,2018.JI Hongli, QIU Jinhao, ZHAO Jinling.Semi active control of structural vibration-synchronized switch damping technique based piezoelectric elements[M].Beijing:Science Press,2018.
[18]汪瑞,闫宇飞,许锋.基于最优控制策略的起落架振动半主动抑制研究[J].控制工程,2023,30(6):1024-1029,1035.WANG Rui, YAN Yufei, XU Feng.Research on semi-active suppression of landing gear vibration based on optimal control strategy[J].Control Engineering of China,2023,30(6):1024-1029,1035.
[19]熊子珺,刘磊,杨鸿杰.基于自适应LMS算法的空间光束快速精扫描跟踪控制方法[J].中国空间科学技术,2021,41(5):95-102.XIONG Zijun,LIU Lei,YANG Hongjie.Fast and precises canning and tracking control of space beam based on adaptive LMS algorithm[J].Chinese Space Science and Technology,2021,41(5):95-102.