0 引言
滚动轴承是设备传动装置功能实现的关键部件,其运行状态是传动装置运行状态的重要表征。由于滚动轴承运行环境较为复杂,振动信号易受环境噪声的影响,极大影响了轴承故障的识别正确率。因此,有效信号与噪声的分离是故障识别的关键。
Dragomiretskiy[1]提出了变分模态分解方法,采用了非递归的分解模式,通过构造变分问题来确定所分解模态的中心频率和模态,实现各分量的有效分离。但变分模态分解方法受模态分量个数K和惩罚因子α的影响较大,K值的选择决定了故障特征频率所处共振频带的位置,α的选择影响了分解后进行信号重构的精度。石文杰等[2]采用微分搜索(DS)算法对VMD进行优化,实现信号的自适应分解,并对各分量进行加权重构。唐贵基等[3]提出了一种基于包络谱特征因子的影响参数自动搜寻策略,减少了人为主观选择对参数的影响。上述方法没有全面考虑2个参数之间的相互影响。因此,本文拟采用遗传算法对VMD进行优化,并选取振动信号的样本熵作为适应度函数,进而确定VMD的最优参数组合[K,α],提高VMD算法的自适应分解效果。
文献检索发现,许多研究中通过直接去除高频模态分量的方式实现信号的降噪。如:刘迎松等[4]利用VMD对故障信号进行自适应分解后,构建加权峭度指标来筛选有效模态分量;梁喆等[5]提出了一种基于经验模态分解和互信息熵的自适应提取算法,通过去除高频分量达到降噪的效果。若将高频IMF分量直接舍弃会导致信号细节和边缘信息丢失,通过对高低频分界点处IMF分量进行二次分解并进一步筛选,能够保留高频噪声中的有效信号,使重构后的信号更接近真实振动信号。
在轴承故障识别算法中,相对于人工神经网络(ANN)[6]、K近邻算法(KNN)[7]等机器学习算法,卷积神经网络(CNN)[8]能够自适应进行特征提取和识别,具有良好的分类正确率。丁承君等[9]利用VMD对振动信号进行分解,将构造的多维IMF矩阵作为深度卷积神经网络的输入进行故障诊断。魏轩等[10]提出了一种深度卷积神经网络与极限学习机相结合的方法,实现了轴承“端到端”的故障诊断。上述方法都是对单一的时域或频域进行学习,所提取特征不能同时表达信号的幅值特征和频率成分。短时傅里叶变换[11]、连续小波变换[12]、和同步压缩变换[13]等时频分析方法相对时域分析法或频域分析法不仅能更好地观察信号的时变特点,还可以表征信号的强度和能量,进而使得网络对信号中的特征学习更加充分、更加完备。例如,李志农等[14]通过结合解调手段与变分模态分解有效处理频率交叉的非平稳信号,并对该重构信号进行同步压缩处理。为进一步提高信号时频谱图的分辨率,采用自适应同步压缩小波变换对各IMF分量进行分析。并在此基础上,利用优化算法对卷积神经网络模型的超参数进行优化,可以提高模型的训练效率和识别正确率。
基于上述分析,运用AVMD-ASWT模型获得高分辨率的少噪声时频图像,可以显著降低信号中噪声的影响,在此基础上结合PCNN模型,可以显著提高滚动轴承故障的识别正确率。
1 AVMD-ASWT-PCNN方法原理
1.1 自适应变分模态分解
自适应变分模态分解算法(AVMD)利用遗传算法(GA)的全局搜索能力对目标函数所在的解空间进行全局寻优,能够得到VMD最优的参数组合。其中,VMD的核心思想是构建和求解变分问题,具体求解过程见文献[1]。AVMD的具体实施步骤如下:
1) 首先,输入原始振动信号,设定K和α的搜寻范围,并初始化GA各项参数,生成初始种群,且每个个体均包含分解层数K和惩罚因子α。
2) 由于样本熵可以反映轴承振动信号中的随机程度和复杂程度,故将其作为GA的适应度函数。计算种群中染色体适应度值,通过适应度值来评价个体与最优值的距离,适应度值越大,该个体遗传到下一代的概率就越大。轴承原始振动信号经AVMD分解后的分量{x(n)}=x(1),x(2),…,x(N)的样本熵可以表示为
![]()
(1)
3) 根据各个染色体的适应度值,抛弃一部分无用染色体,结合相关概率,对剩下的染色体进行交叉、变异,形成新的种群。
4) 计算新种群的适应度并根据适应度进行排序,逐渐将种群优化至包含最优解的状态,得到最优的参数组合。
1.2 自适应同步压缩小波变换
同步压缩小波变换(SWT)[15]是将小波变换与时频谱重排算法相结合的一种全新的时频分析方法。对信号进行连续小波变换后,采用同步压缩算法(SST)[16]将时间-尺度平面的信息转化到时间-频率平面,使得时频图像的能量更加集中。
传统同步压缩小波变换方法中小波基函数选择随意性较大,部分信号的能量谱具有发散的问题。若在进行同步压缩小波变换时,根据信号频率的高低采取不同的小波基函数进行时频分析,能保证高频分量和低频分量同时具有较高的时频聚集性和时频分辨率,进而得到高分辨率的少噪声时频图像。同时,引入Rényi熵来衡量所生成分量时频图像的分辨率,Rényi熵越小表明图像时频分辨率越高,Rényi熵的表达式如下,式(2)中α取值为3。

(2)
1.3 互信息熵-相关系数准则
采用AVMD对信号进行分解后,需要对IMF分量进行筛选,并准确区分噪声分量和有效分量。通常在高频分量和低频分量的分界点相邻两侧,表征高频噪声成分的IMF分量中,除包含噪声外,还含有部分表征信号特征的有效信息,而低频有效信号中也可能含有少量的噪声。若直接根据经验将高频IMF分量舍弃而重构低频分量则会导致信号细节和边缘信息丢失,造成降噪效果不佳。
由于高频噪声对分量的依存性较低,低频有效信号对分量的依存性较高,故将分解后的IMF分量作互信息熵计算,计算得到的首个局部极小值即为高频分量与低频分量的分界点。互信息熵的表达式为
![]()
(3)
式(3)中: p(xi,yi)为联合概率分布,p(xi)和p(yi)为边缘概率分布,X和Y表示相邻的IMF分量。
为平衡筛选过程中同时包含有效信息和噪声信息的IMF分量,计算各个分量的相关系数,并结合方差贡献率判断各分量对信号影响程度的大小。对分界点相邻两侧相关性较低的IMF分量进行二次分解,进而将高频噪声中的有效信号进行保留,同时将低频信号中的少量噪声滤除。
1.4 粒子群优化卷积神经网络
卷积神经网络模型的参数对其识别性能影响较大,在构建网络模型时往往需要反复的试验和经验来确定最优的模型参数。粒子群算法[17]通过模拟鸟类觅食来搜寻粒子的全局最优值,因此,可通过PSO算法选取模型关键参数,进而构建自适应卷积神经网络。其中,需要优化的模型参数包括迭代次数(epoch),批处理大小(batch size),学习率(lr),Dropout值和卷积核大小。
粒子群算法中惯性权重ω若根据经验选定,容易出现早熟收敛、陷入局部最优等情况,故采用自适应方式修正惯性权重,惯性权重随粒子目标函数值的改变而改变。动态惯性权重粒子群优化卷积神经网络模型的具体步骤如下:
1) 初始化CNN模型及PSO算法参数,设置种群数量和迭代次数等参数。
2) 计算每个粒子在该位置对应的适应度值,选择测试集识别正确率作为适应度,确定最佳粒子位置。
3) 更新各粒子位置和速度,更新惯性权重ω,得到个体、全局最优极值。
4) 满足迭代结束条件后,输出最终的粒子群寻优结果,利用得到的最佳参数组合构建网络模型。
2 AVMD-ASWT-PCNN故障识别
2.1 AVMD-ASWT-PCNN方法步骤
本文所提AVMD-ASWT-PCNN时频图像故障识别方法如图1所示。

图1 AVMD-ASWT-PCNN故障识别方法流程
Fig.1 AVMD-ASWT-PCNN fault identification method flowchart
具体步骤如下:
1) 采用AVMD-ASWT算法对轴承振动信号进行预处理,其中,AVMD可将信号自适应分解为一系列固有模态分量,ASWT可将IMF分量转换为高分辨率的分量时频图像。
2) 计算相邻分量的互信息熵,区分高频分量和低频分量,并将高、低频分界点相邻两侧的分量进行二次分解,获得二次分解的分量时频图像。
3) 依据相关系数和方差贡献率对两次分解的IMF分量进行筛选,得到有效分量时频图像,将有效分量时频图像进行重构得到少噪声时频图像。
4) 采用动态惯性权重PSO算法对卷积神经网络模型的参数进行优化,构建最优网络模型。
5) 构建少噪声时频图像数据集,将其作为PCNN模型的输入进行特征提取和故障识别。
2.2 实例验证
2.2.1 AVMD-ASWT时频图像生成
采用CWRU公开轴承数据集作为原始数据,在振动信号中加入信噪比为2 dB的高斯白噪声,如图2所示。采用AVMD算法对信号进行自适应分解,根据经验设定参数K的范围为[3,10],α的范围为[500,2 500]。经过算法迭代优化,得到最优参数值K=8,α=2 289,适应度函数的迭代曲线如图3所示。
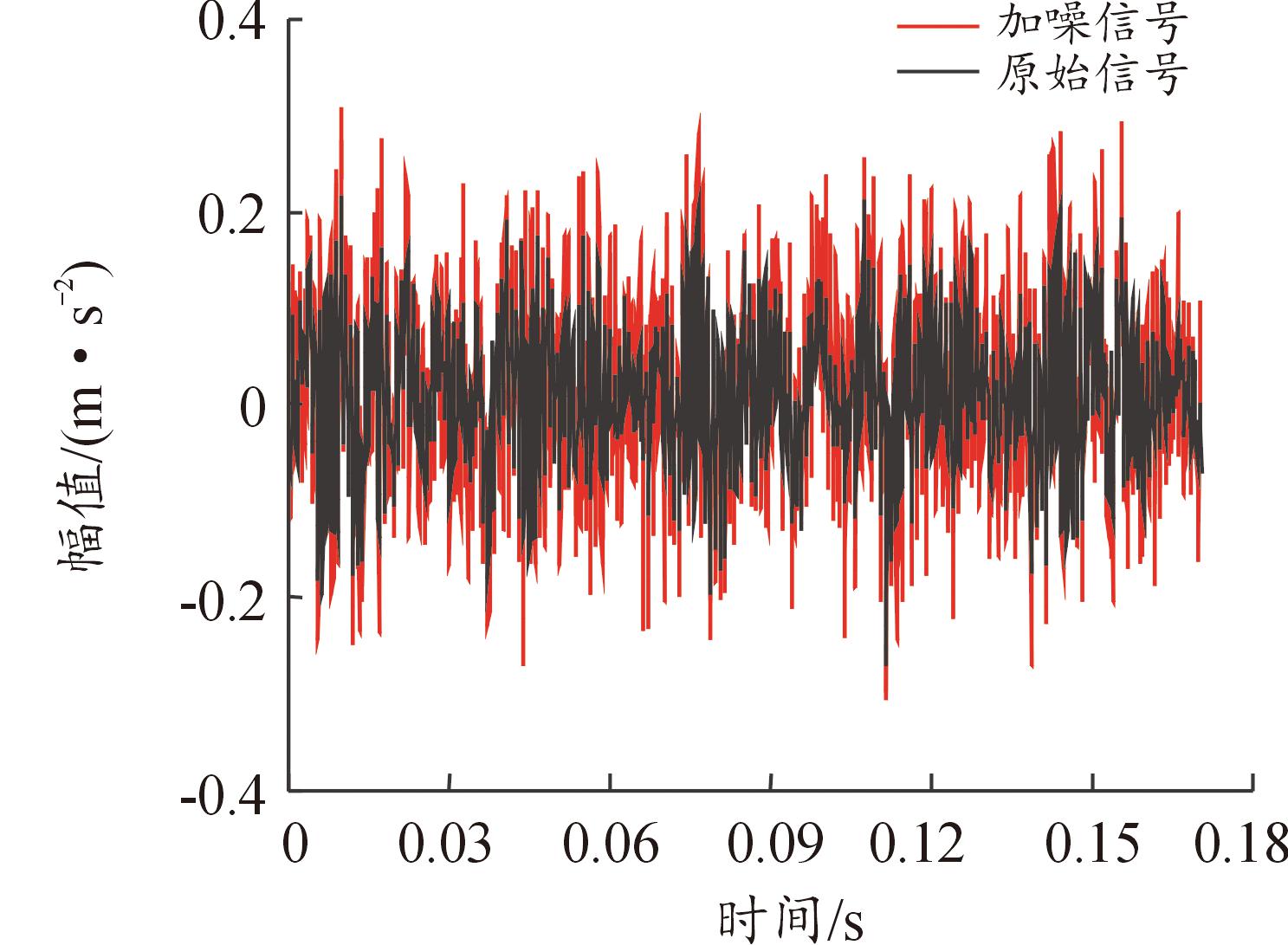
图2 原始振动信号和加噪振动信号
Fig.2 Original and noise-added vibration signals
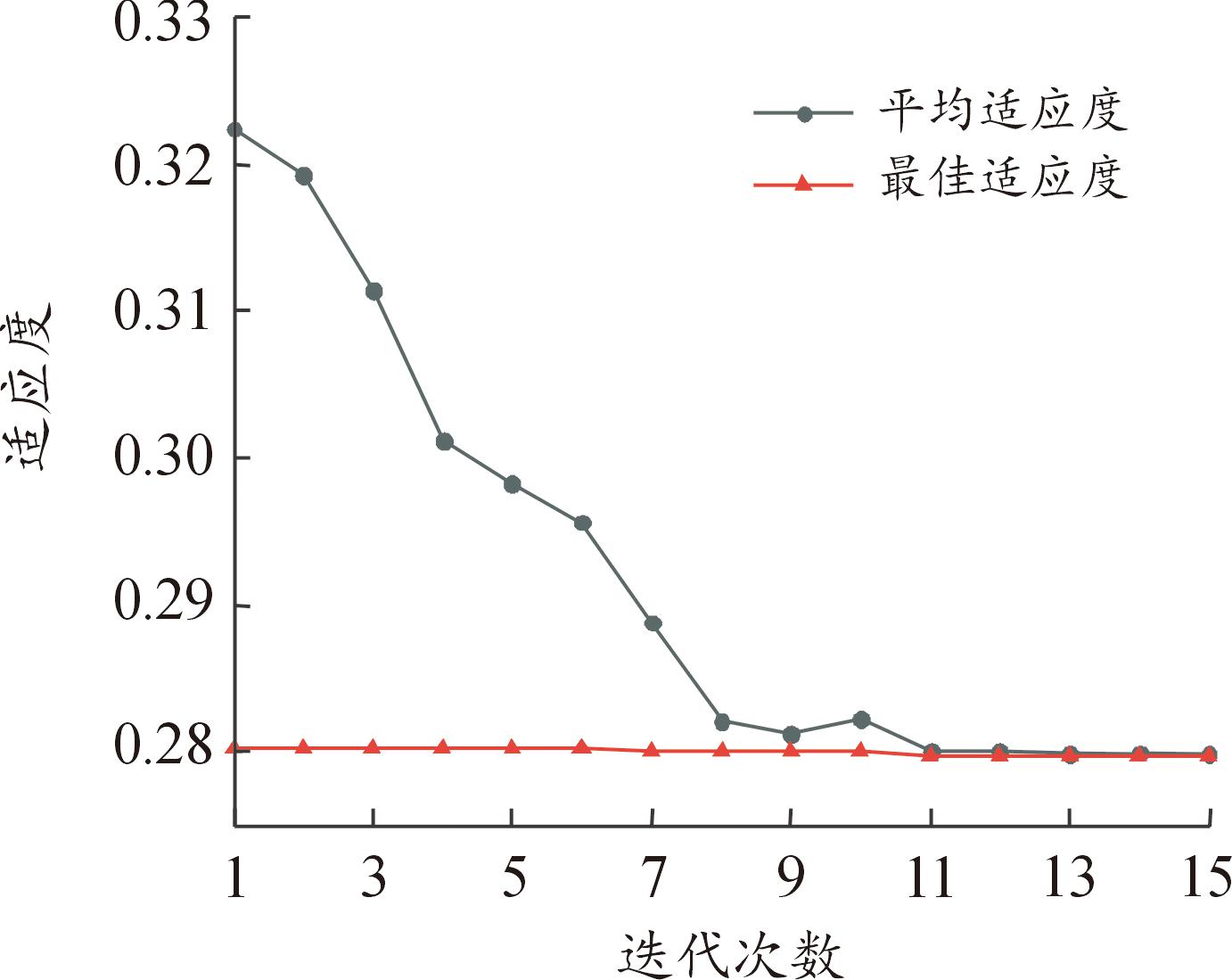
图3 适应度函数迭代曲线
Fig.3 Iterative curve of the fitness function
根据各分量频率高低,采用不同小波基函数的ASWT进行分析,所生成分量时频图像的Rényi熵值如图4所示,经AVMD分解得到的IMF分量及其对应的局部时频图如图5所示。

图4 IMF分量Rényi熵对比
Fig.4 Comparison of Rényi entropy of IMF components

图5 AVMD分解结果及分量SWT时频图
Fig.5 Decomposition results and corresponding time-frequency diagrams
其中,当IMF分量频率为600~2 400 Hz (IMF2~IMF4)时,采用Bump函数所得到的分量时频图像分辨率更高,而当频率低于600 Hz(IMF1)和高于2 400 Hz(IMF5~IMF8)时,分别采用Morlet函数和Shannon函数能得到更高分辨率的分量时频图像。
依次计算相邻IMF分量的互信息熵,如图6所示,IMF4为第一个极小值点,即信号高频分量和低频分量的分界点。然后,计算各个分量与原始信号的相关系数,并结合方差贡献率校核上述选择的可行性,结果如表1所示。AVMD分解得到的7个IMF分量和Res分量中,IMF1和IMF2的相关系数均超过了0.5,而IMF6和IMF7的相关系数低于0.01,说明IMF1和IMF2为有效分量,IMF6和IMF7为噪声分量。
表1 IMF分量相关系数和方差贡献率
Table 1 Correlation coefficient and variance contribution of the IMF

模态分量相关系数方差贡献率/%模态分量相关系数方差贡献率/%IMF10.50530.2277IMF50.01090.0321IMF20.77570.5338IMF60.00180.0344IMF30.08760.0344IMF70.00700.0338IMF40.18220.0695Res0.00120.0338
表2 不同方法所生成时频图像Rényi熵
Table 2 Entropy of Rényi for different time-frequency diagrams

时频图SWTSSTFTCWTSTFT加噪信号14.7317.8518.5719.89去噪信号11.9915.7515.0817.73

图6 相邻IMF分量互信息熵
Fig.6 Mutual information entropy of adjacent IMFs
由于分界点相邻两侧的分量同时含有噪声和有效信息,故将IMF3、IMF4和IMF5分量重构并进行二次分解,过程与上述步骤相同。AVMD算法最佳参数组合[K,α]=[9,1 645],计算各分量相关系数和方差贡献率,其中,IMF4的相关系数和方差贡献率最大,分别为0.188 6和0.334 6。
将两次分解筛选得到的分量时频图像进行重构,获得的少噪声时频图像如图7(a)所示,ASWT逆变换后得到的时域图像如图8所示。经计算,AVMD一次分解得到的低频分量相关系数为0.914 6,而二次分解后重构的信号相关系数为0.935,且信噪比提高了1.868 2 dB。可以看出,信号中大部分噪声干扰均被去除,且最大程度上重构了信号。
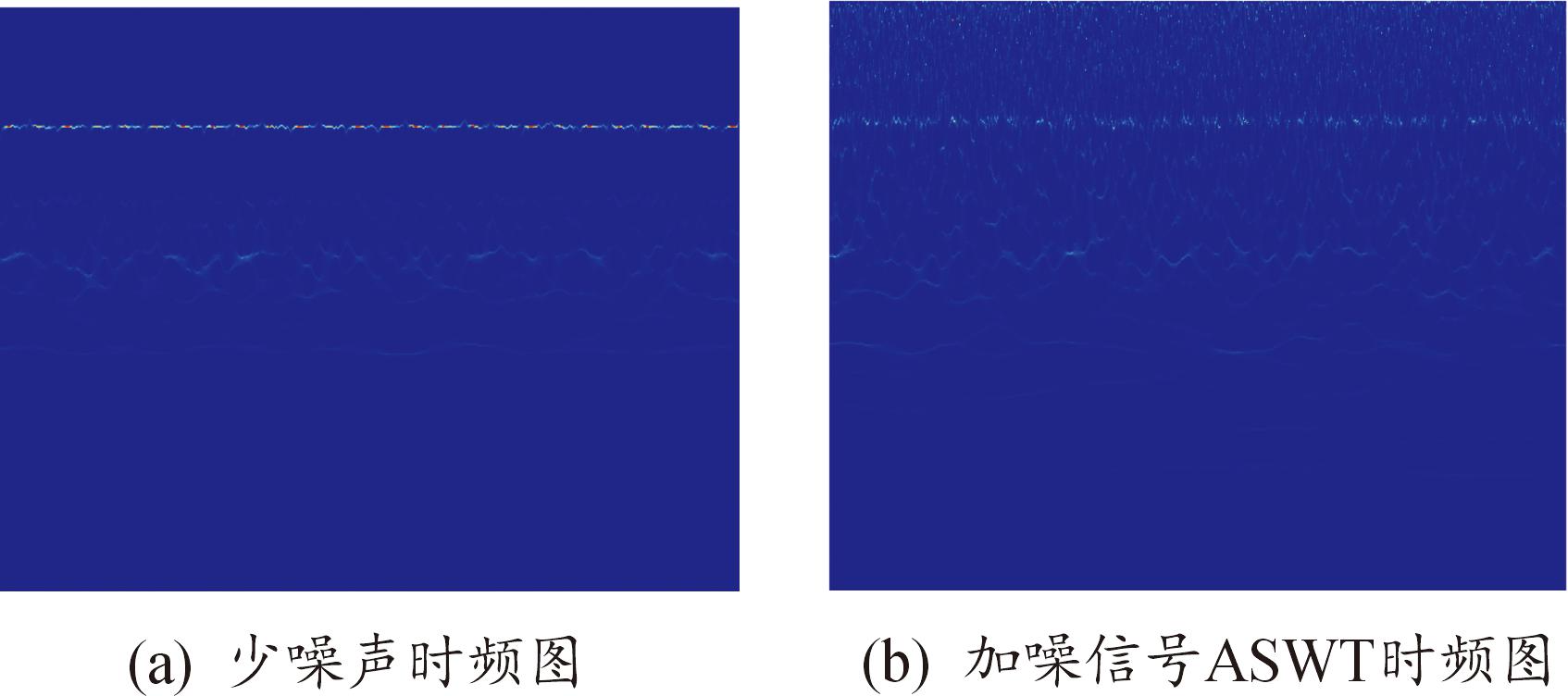
图7 信号降噪前后ASWT时频图
Fig.7 ASWT diagram before and after signal noise reduction

图8 ASWT时频图逆变换
Fig.8 Inverted transformation of ASWT time-frequency diagram
采用信噪比和均方根误差作为评价指标,定量分析本文方法在不同噪声条件的降噪效果。从图9中可以看出,利用本文的降噪方法,加入不同噪声强度的信号信噪比均得到提升,均方根误差均有不同程度的减小,且两个指标显著好于常用的小波降噪方法。
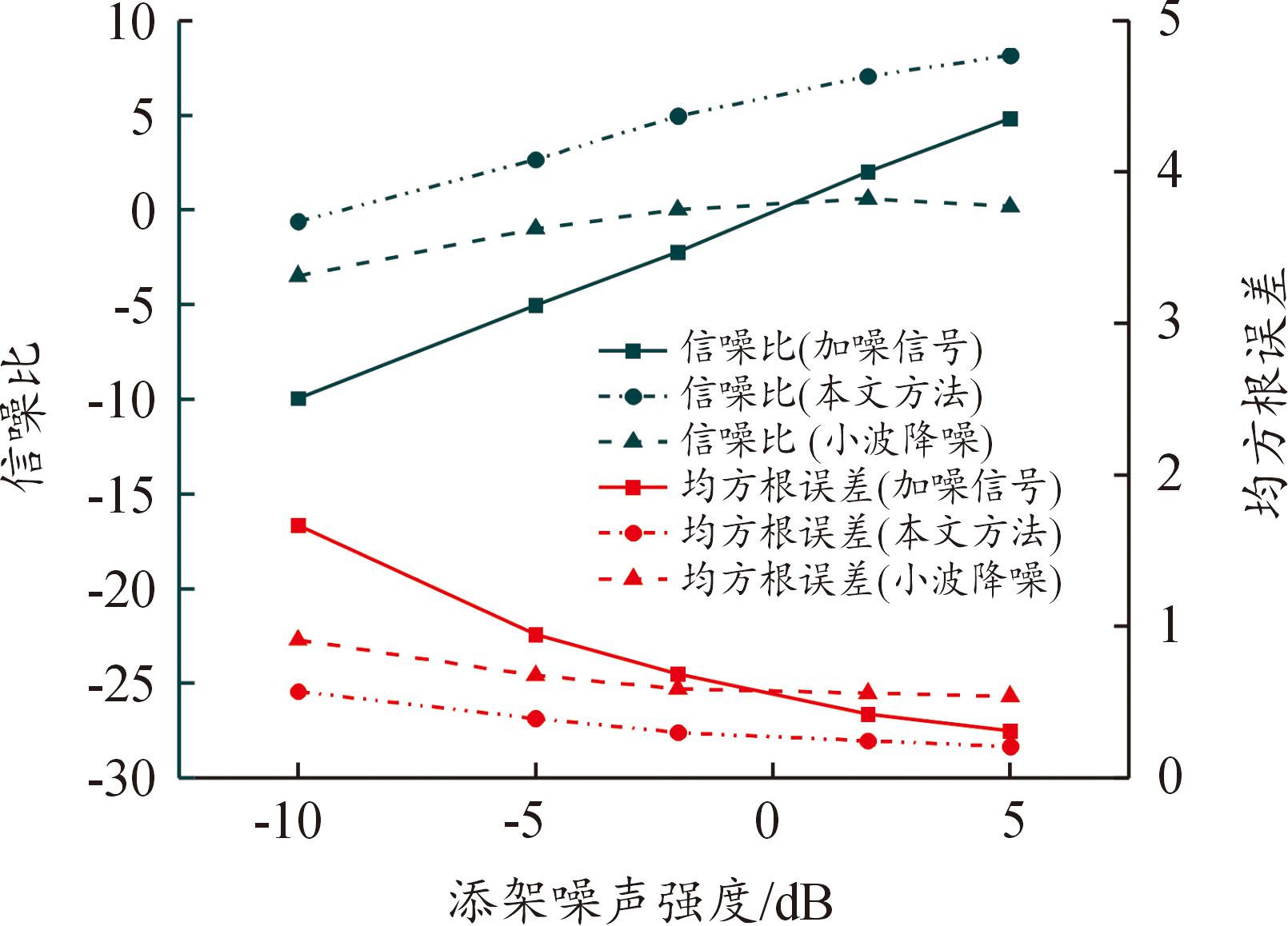
图9 不同噪声强度下信号信噪比和均方根误差变化
Fig.9 Signal-to-noise ratio and root-mean-square error of signals with different noise
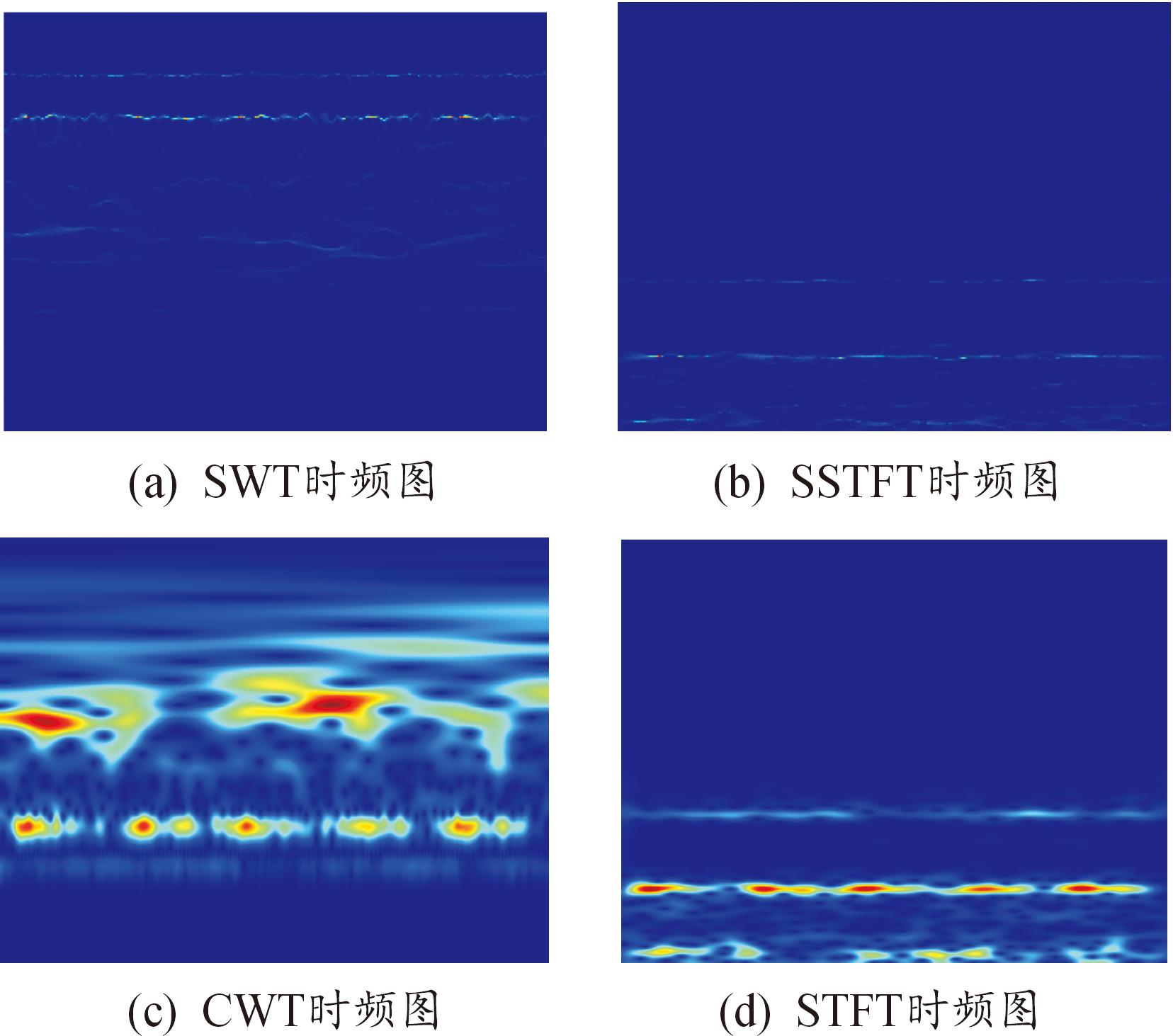
图10 不同时频分析方法时频图
Fig.10 Time-frequency diagram of different time-frequency analysis methods
作为对比,对振动信号分别进行同步压缩傅里叶变换(SSTFT)、连续小波变换(CWT)和短时傅里叶变换(STFT),并计算生成时频图像的Rényi熵。其中,SWT的熵值最小,时频分辨率最高,且通过同步压缩算法得到的时频图像显著提高了时频聚集性。故选取SWT时频图像作为卷积神经网络模型的输入。
2.2.2 PCNN故障识别
选用CWRU数据集中电机负载为0 HP,采样频率为12 kHz,转速为1 797 r/min状态下的驱动端滚动轴承振动信号作为数据集,包含轴承在不同故障形式的10种运行状态下的共4 343 个样本。
利用动态惯性权重PSO算法对CNN模型参数进行优化,以测试集的损失值作为适应度函数的目标值,PSO相关参数和CNN网络模型结构如表3和表4所示。网络模型中输入图像的大小为128×128,激活函数选择ReLU函数,分类器选择Softmax分类器,引入Dropout层防止网络模型过拟合,并采用稀疏多分类交叉熵作为损失函数,如式(4)所示。
![]()
(4)
表3 动态惯性权重PSO相关参数
Table 3 Related parameters of PSO

参数取值范围数值epoch10~6028lr0.0001-0.010.0016batchsize8~12838卷积层大小2~73池化层大小2~72
续表(表3)

参数取值范围数值Dropout0.2~0.60.252加速度因子c1c2-2惯性权重ωmax-0.9惯性权重ωmin0.4种群数量-10
表4 卷积神经网络结构参数
Table 4 Parameters of convolutional neural network structure

网络层核大小步长通道数输出大小Conv2D-13×31×18128×128×8MaxPooling-12×22×2864×64×8Dropout0.252--64×64×8Conv2D-23×31×11664×64×16MaxPooling-22×22×21632×32×16Dropout0.252--32×32×16Flatten----Dense-132-132Dense-210-110
式(4)中,![]() 表示第i个样本,属于第m个类别。
表示第i个样本,属于第m个类别。
分别将加噪时域信号、原始时域信号、频域信号和时频图像作为输入进行对比。从识别正确率(图11)和损失函数变化曲线(图12)中可以看出,以时频图像作为输入的模型识别正确率要好于其他模型。同时,选用CWRU数据集中电机负载为0、1、2、3 HP的4种不同工况下驱动端和风扇端的轴承数据来进行验证,得到的识别正确率如图13所示,平均正确率达到96.19%。

图11 不同模型识别正确率变化曲线
Fig.11 Recognition accuracy curves for different models

图12 不同模型损失值变化曲线
Fig.12 Loss value curves for different models
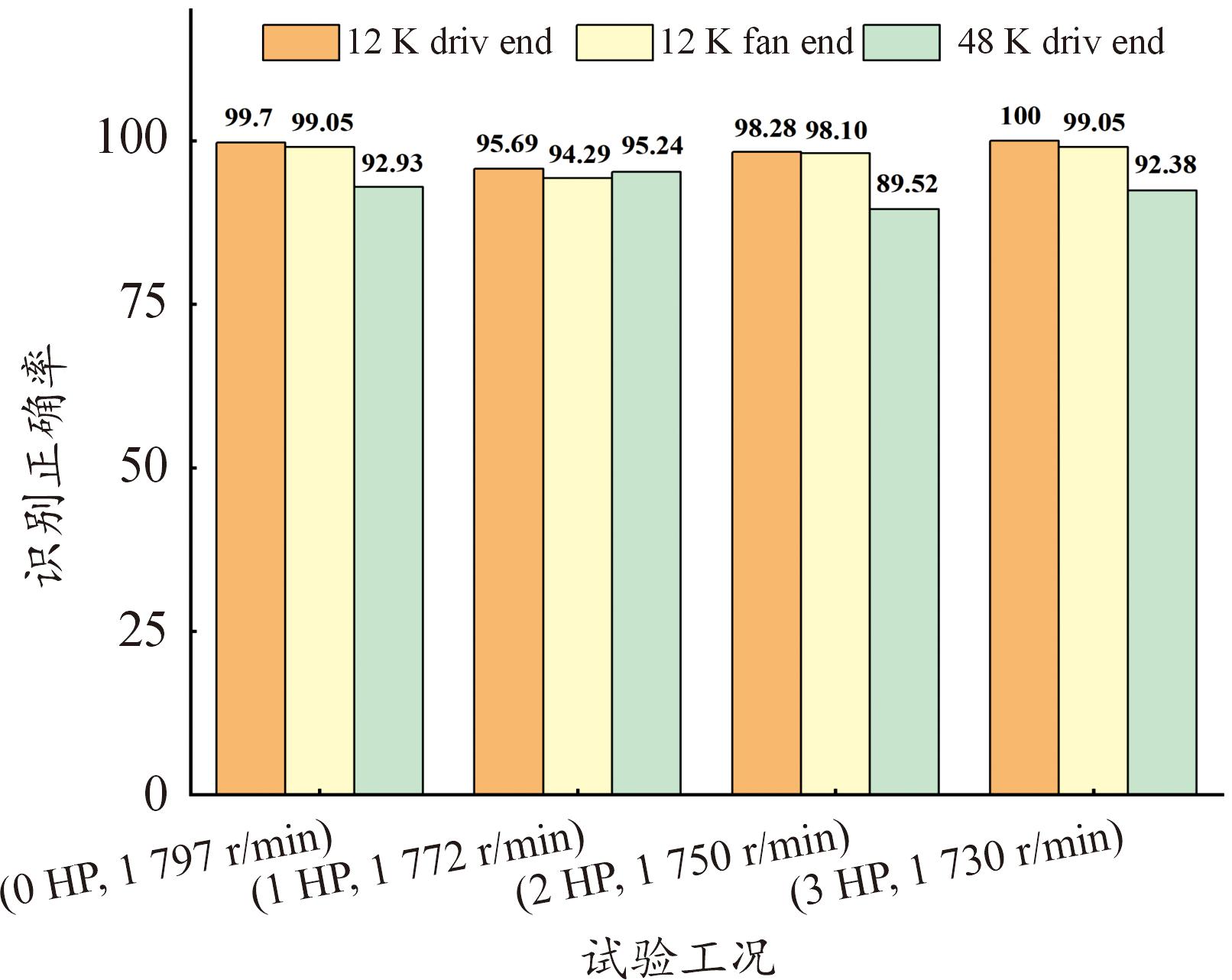
图13 不同试验工况下识别正确率
Fig.13 Recognition accuracy under different test conditions
3 工程应用
为了验证本文方法在实际复杂工况下的性能,采用滚动轴承性能试验台模拟轴承运行状态,试验台如图14(a)所示,试验轴承选用NU206E圆柱滚子轴承,轴承参数如表5所示。试验通过液压加载装置,对外圈施加10.54 kN的径向载荷,转速为5 000 r/min,润滑方式采用喷油润滑。采用IEPE电压输出加速度传感器和亿恒公司的MI-7008信号采集与分析仪采集轴承振动加速度信号,采集仪采样频率为25 600 Hz。
表5 试验轴承基本参数
Table 5 Structural parameters of the test bearing

参数数值参数数值内径/mm30滚子直径/mm8.5外径/mm62滚子个数/个13

图14 试验设备
Fig.14 Test equipment
图15为圆柱滚子轴承试验中所出现的滚动体故障、内圈故障、外圈故障以及滚动体与内圈的复合故障和所对应时频图像。从4类故障类型和正常运行状态中随机选出1 250个样本作为少噪声时频图像数据集输入网络模型中。

图15 轴承各类故障及时频图
Fig.15 Bearing faults and time-frequency diagrams
以圆柱滚子轴承内圈剥落故障为例,对信号进行降噪处理,降噪前后时频图像如图16所示。

图16 轴承内圈剥落故障降噪过程
Fig.16 The process of reducing noise in bearings with spalled inner ring failures
采用PCNN模型对轴承信号进行故障识别,图17为故障识别正确率曲线与损失函数变化曲线,模型训练集准确率迅速提升并稳定在99%左右,验证集正确率和损失率呈现同样趋势。

图17 模型识别正确率和损失率曲线
Fig.17 Recognition correctness and loss rate curves for the model
为了显示PCNN提取故障特征的能力,将数据集样本输入模型中,通过t分布随机邻域嵌入(t-SNE)三维立体可视化模型的分类效果。从图18中可以看出,数据集在输入层时区分度较低,经过卷积操作后,故障特征表达已经明显线性可分且聚集性显著提高。

图18 数据集t-SNE可视化
Fig.18 t-SNE visualisation image of the dataset
为了验证所提出模型的性能,基于相同时频图像数据集,以识别正确率和标准差为考核指标,分别与经典的MobileNet、ResNet、DenseNet、ConvNet深度学习模型进行了对比,每种模型进行5 次重复测试,如图19所示,得到各模型的平均识别正确率分别为65.92±2.49、86.26±1.50、95.92±0.92和95.6±1.69。与其他模型相比较,本文所构建网络模型的平均正确率达到了99.10%±0.58,具有更高的识别正确率和更小的标准差,由此证明了所提方法能够准确稳定地区分滚动轴承在实际工况中出现的不同故障类型。

图19 不同模型识别正确率对比
Fig.19 Recognition accuracy of different models
4 结论
1) 采用AVMD-ASWT对轴承振动信号进行二次处理,并结合互信息熵-相关系数准则进行筛选,在去除噪声的同时最大程度保留了信号中的有效信息;且在不同信噪比的噪声环境下,均取得了较好的降噪效果。
2) 采用AVMD-ASWT所得到的ASWT时频图像具有更高的时频聚集性和分辨率,将其作为网络模型输入的识别正确率显著高于时域信号和频域信号作为输入的识别正确率。
3) 试验结果表明,所提PCNN模型的识别正确率和识别速度相较其他网络模型有明显提升和改进,为快速、准确识别滚动轴承发生的故障类型提供了一种可行方案。
[1] DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing,2013,62(3):531-544.
[2] 石文杰,黄鑫,温广瑞,等.基于DS-VMD及相关峭度的滚动轴承故障诊断[J].振动、测试与诊断,2021,41(1):133-141.SHI Wenjie,HUANG Xing,WEN Guangrui,et al.Rolling bearing fault diagnosis based on DS-VMD and correlated kurtosis[J].Journal of Vibration,Measurement and Diagnosis,2021,41(1):133-141.
[3] 唐贵基,王晓龙.变分模态分解方法及其在滚动轴承早期故障诊断中的应用[J].振动工程学报,2016,29(4):638-648.TANG Guiji,WANG Xiaolong.Variational modal decomposition method and its application in early fault diagnosis of rolling bearings[J].Journal of Vibration Engineering,2016,29(4):638-648.
[4] 刘迎松,魏志刚,束海星等.基于参数自适应VMD和MCKD的滚动轴承微弱故障特征提取[J].噪声与振动控制,2023,43(3):102-109.LIU Yingsong,WEI Zhigang,SHU Haixing et al.Weak fault feature extraction for rolling bearings based on parameter adaptive VMD and MCKD[J].Noise and Vibration Control,2023,43(3):102-109.
[5] 梁喆,彭苏萍,郑晶.基于EMD和互信息熵的微震信号自适应去噪[J].计算机工程与应用,2014,50(4):7-11,32.LIANG Che,PENG Suping,ZHENG Jing.Adaptive denoising of microseismic signals based on EMD and mutual information entropy[J].Computer Engineering and Applications,2014,50(4):7-11,32.
[6] ZHU X,XIONG J,LIANG Q.Fault diagnosis of rotation machinery based on support vector machine optimized by quantum genetic algorithm[J].IEEE Access,2018,6:33583-33588.
[7] HE D,LI R,ZHU J,et al.Data mining based full ceramic bearing fault diagnostic system using AE sensors[J].IEEE Transactions on Neural Networks,2011,22(12):2022-2031.
[8] LIANG P,DENG C,WU J,et al.Intelligent fault diagnosis of rotating machinery via wavelet transform,generative adversarial nets and convolutional neural network[J].Measurement,2020,159:107768.
[9] 丁承君,冯玉伯,王曼娜.基于变分模态分解与深度卷积神经网络的滚动轴承故障诊断[J].振动与冲击,2021,40(2):287-296.DING Chengjun,FENG Yubo,WANG Manna.Fault diagnosis of rolling bearings based on variational modal decomposition and deep convolutional neural network[J].Vibration and Shock,2021,40(2):287-296.
[10] 魏轩,慕晓冬,曾昭菊,等.基于残差网络的航天器测控系统诊断[J].兵器装备工程学报,2023,44(3):254-260.WEI Xuan,MU Xiaodong,ZENG Zhaoju,et al.Fault diagnosis of spacecraft tracking telemetry and control systems based on residual network[J].Journal of Ordnance Equipment Engineering,2023,44(3):254-260.
[11] JAWADEKAR A,PARASKAR S,JADHAV S,et al.Artificial neural network-based induction motor fault classifier using continuous wavelet transform[J].Systems Science &Control Engineering,2014,2(1):684-690.
[12] HAN T,CHAO Z.Fault diagnosis of rolling bearing with uneven data distribution based on continuous wavelet transform and deep convolution generated adversarial network[J].Journal of the Brazilian Society of Mechanical Sciences and Engineering,2021,43(9):425.
[13] LI C,LIANG M.Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform[J].Mechanical Systems and Signal Processing,2012,26:205-217.
[14] 李志农,胡志峰,毛清华,等.非线性调频模态分解-同步提取变换方法及其在滚动轴承故障诊断中的应用[J].兵工学报,2021,42(6):1324-1330.LI Zhinong,HU Zhifeng,MAO Qinghua,et al.Nonlinear FM modal decomposition-synchronous extraction transformation method and its application in rolling bearing fault diagnosis[J].Journal of Military Engineering,2021,42(6):1324-1330.
[15] 陈小旺,冯志鹏.基于迭代广义同步压缩变换的时变工况行星齿轮箱故障诊断[J].机械工程学报,2015,51(1):131-137.CHEN Xiaowang,FENG Zhipeng.Fault diagnosis of planetary gearboxes with time-varying operating conditions based on iterative generalized synchronous compression transformation[J].Journal of Mechanical Engineering,2015,51(1):131-137.
[16] 胡志峰,李志农,朱彤等.基于同步提取变换的滚动轴承微弱特征增强与提取方法[J].兵器装备工程学报,2021,42(2):234-238.HU Zhifeng,LI Zhinong,ZHU Tong et al.Weak feature enhancement and extraction method for rolling bearings based on simultaneous extraction transform[J].Journal of Ordnance Equipment Engineering,2021,42(2):234-238.
[17] 杨超,张开富.基于PSO-BiLSTM神经网络的机身筒段应力预测[J].航空学报,2023,44(7):266-275.YANG Chao,ZHANG Kaifu.Stress prediction of fuselage barrel section based on PSO-BiLSTM neural network[J].Journal of Aeronautics,2023,44(7):266-275.