0 引言
自抗扰控制(ADRC)采用扩张状态观测器(ESO)估计被控系统内部不确定性和外部扰动,并通过非线性状态误差反馈进行动态补偿[1],从而具有很强的鲁棒性和控制性能。线性自抗扰控制(LADRC)通过采用线性扩张状态观测器(LESO)和线性误差反馈函数[2],简化了控制器结构、减少了待整定参数、降低了参数整定难度。
在飞行控制领域,ADRC被广泛应用于多旋翼无人机的姿态控制和轨迹跟踪[3-5]、柔性飞行器姿态控制[7]、无人直升机飞行控制[8]、飞行器着陆控制[9]、高超飞行器再入飞行控制[10]、地效飞行器姿态控制[11]、深空探测航天器姿态控制[12]、空中加油飞行控制[13]、舰载机飞行控制[14-15]等不同方向的研究,取得了较好的控制效果。但在固定翼无人机自主空中加油、空中对接回收等特定应用场景中,无人机飞行高度控制器对控制精度和抗扰性能提出了更高的需求。
一般情况下,LADRC控制器都是采用基于输出的方式进行设计,即LADRC飞行高度控制器将实测的飞行高度作为LESO的输入,再将高度指令值与高度观测值之差输入到状态误差反馈,从而计算得到控制输出。
在一些应用场景中,如无人机自主空中加油对接过程中,通常采用摄像头/激光雷达等设备直接测量无人机与加油锥套之间的相对高度,作为无人机高度控制器的控制输入信息,此时基于输出的LADRC不再适合于飞行高度控制器的设计。
基于误差的LADRC[16-17]控制器,是指在设计LADRC飞行高度控制器时直接采用高度控制误差信息作为LESO的输入。一方面,采用基于误差的LADRC设计无人机飞行高度控制器更加符合工程设计思想;另一方面,采用高度控制误差作为ESO的输入,能够避免或降低ESO在计算初始阶段出现较强的“尖峰效应”[18]。
本文中针对固定翼无人机飞行高度控制开展研究,采用基于误差的一阶LADRC进行无人机高度外环控制器设计,以高度控制误差信息作为LESO的输入信息,实时观测和消除无人机模型的内部和外部扰动,实现对无人机飞行高度的精确控制。
1 无人机飞行高度控制器结构
固定翼无人机的纵向飞行控制通常包括高度控制和速度控制,分别通过升降舵和油门实现。本文中无人机通过调节油门保持恒定空速飞行,而高度控制分为内环控制和外环控制,控制结构如图1所示。高度外环控制器根据高度指令值与高度测量值之差,采用LADRC方法计算生成高度变化率指令。高度内环控制器根据高度变化率指令和无人机高度变化率、迎角、俯仰角等状态量测量值,采用特征结构配置法计算生成升降舵指令。
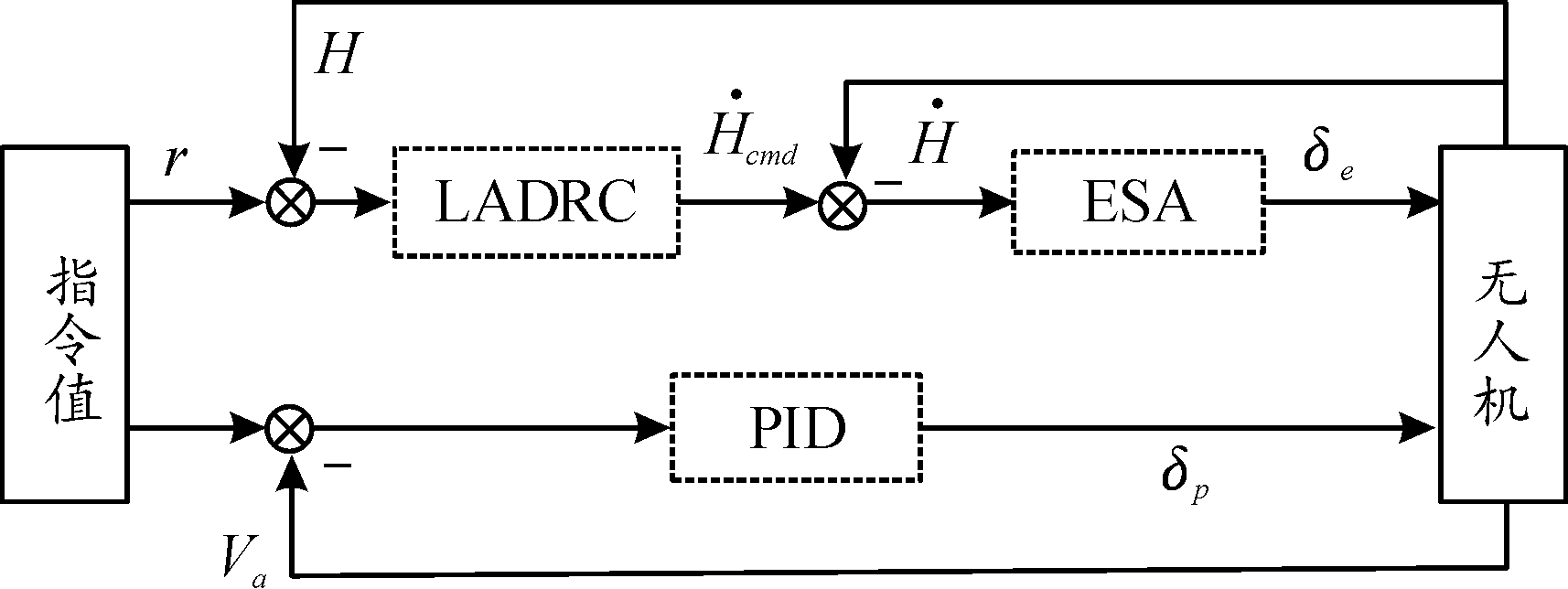
图1 无人机飞行高度控制器结构
Fig.1 UAV flight height control system structure
高度外环控制采用LADRC方法,利用LESO估计出高度外环控制中存在的模型误差、风扰等内部和外部扰动之和,并在控制量中进行动态补偿,从而实现无人机飞行高度的精准控制。
2 基于一阶LADRC的高度外环控制器
高度外环控制的被控对象模型可视为带有未知扰动的一阶系统:
![]()
(1)
式中:H表示无人机飞行高度;u表示高度外环控制器的输出量,即高度变化率指令![]() 表示系统内部和外部的总扰动量;b表示为非零的输入增益。
表示系统内部和外部的总扰动量;b表示为非零的输入增益。
2.1 基于输出的一阶LADRC高度外环控制
设r为高度指令,可以设计线性扩张状态观测器
![]()
(2)
使得:
![]()
(3)
则状态反馈控制律为
![]()
(4)
基于输出的一阶LADRC高度控制的结构如图2所示。
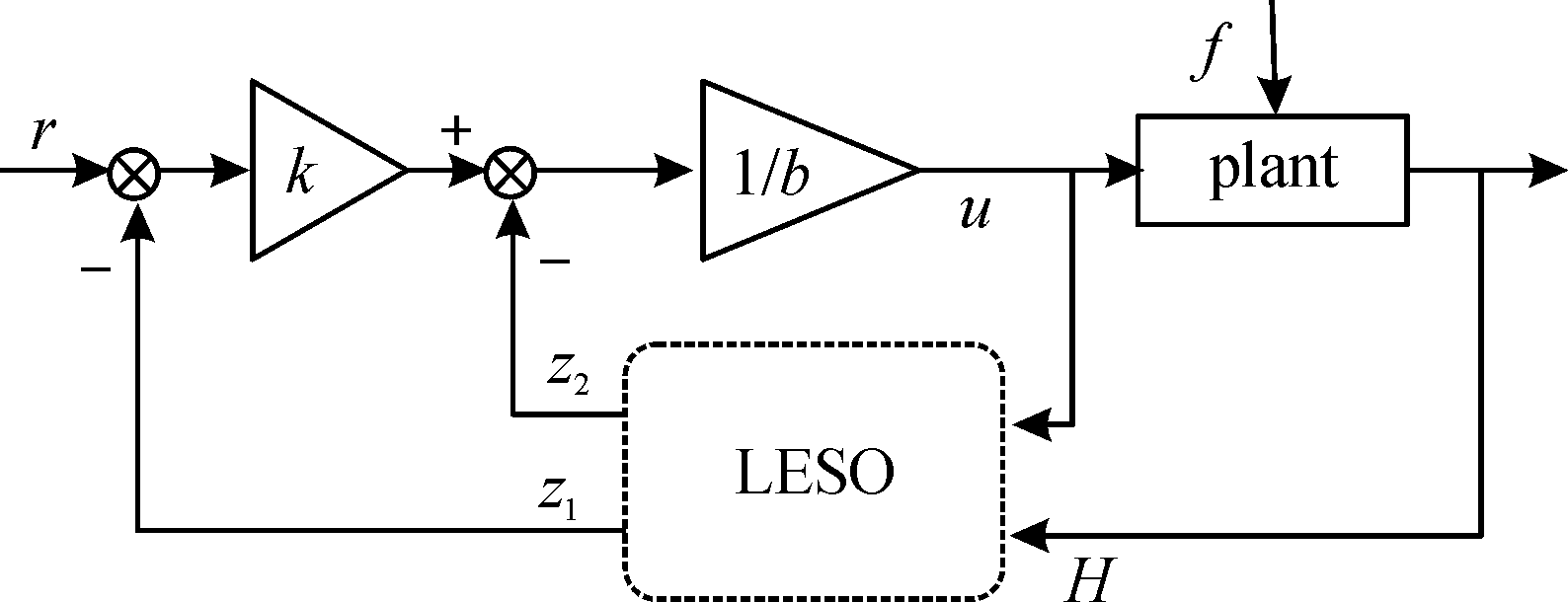
图2 基于输出的一阶LADRC高度控制结构图
Fig.2 Height control system structure of output-based first-order LADRC
2.2 基于误差的一阶LADRC高度外环控制
设r为高度指令,高度的跟踪误差为
e=r-H
(5)
则有:
![]()
(6)
定义![]() 为系统的总扰动量,则有:
为系统的总扰动量,则有:
![]()
(7)
针对上式构建线性扩张状态观测器:
![]()
(8)
取状态反馈控制律为
![]()
(8)
则线性扩张状态观测器的状态空间方程为
![]()
(9)
根据带宽整定方法,设观测器带宽为ωo,则有:
![]()
(10)
通过调整观测器带宽,可以实现:
![]()
(11)
所以,基于误差的一阶LADRC高度控制的结构如图3所示。
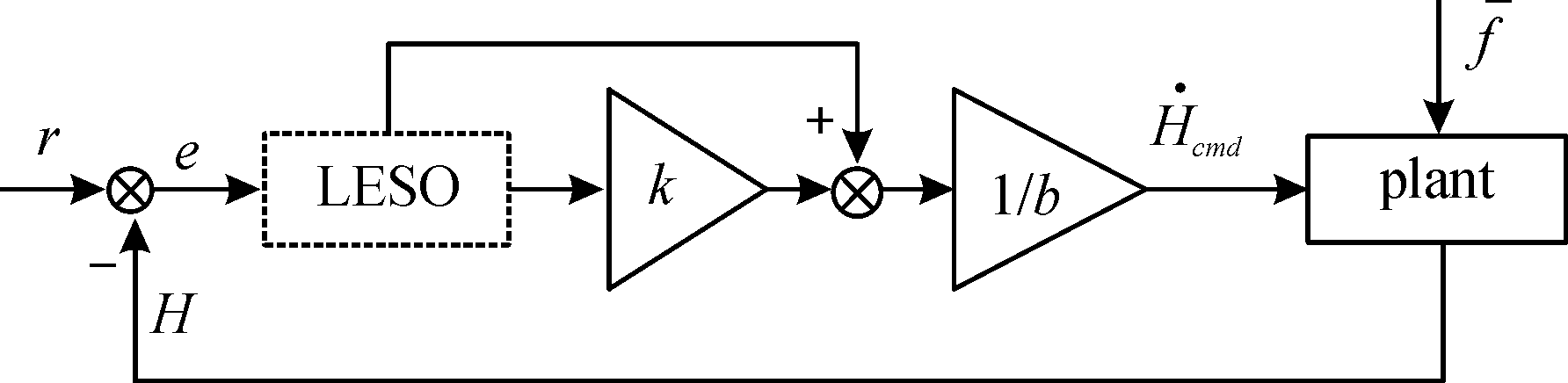
图3 基于误差的一阶LADRC高度控制结构图
Fig.3 Height control system structure of error-based first-order LADRC
3 仿真分析
以常规布局固定翼无人机为研究对象开展数值仿真,无人机关键参数如表1所示。
表1 无人机关键参数
Table 1 Key parameters of UAV
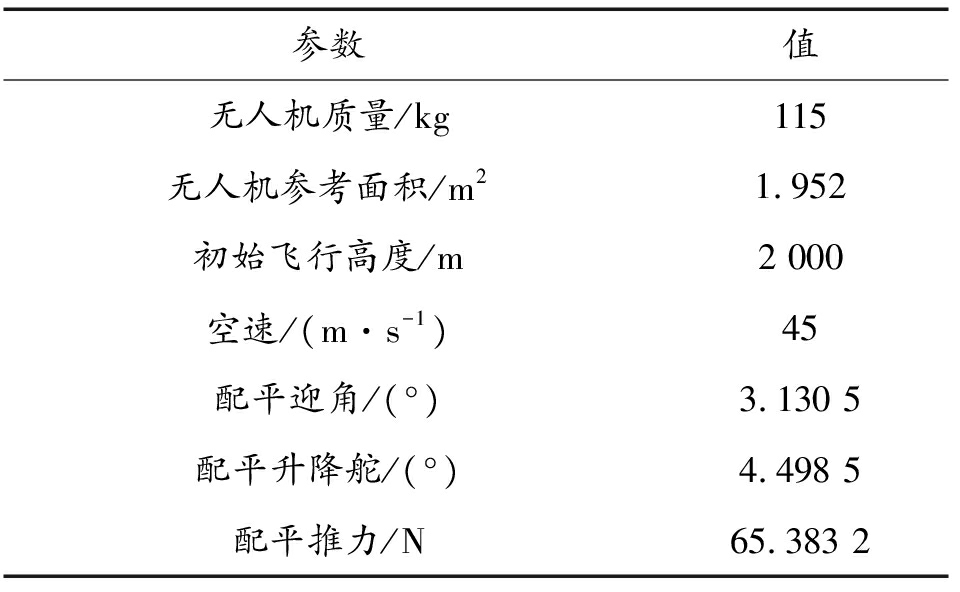
参数值无人机质量/kg115无人机参考面积/m21.952初始飞行高度/m2 000空速/(m·s-1)45配平迎角/(°)3.130 5配平升降舵/(°)4.498 5配平推力/N65.383 2
仿真计算机为联想ThinkBook15,处理器为i5-1135G7@2.40 GHz,内存16 G。
仿真初始状态为无人机定速定高平飞,在仿真15 s时引入30 m的高度阶跃指令,仿真结果见图4—图6。在无风干扰的情况下,飞行15 s左右完成阶跃指令响应,过程稳定,没有超调,见图4。迎角响应过程稳定,先上升到4.421 8°,再下降到2.320 3°,最后回到配平值,始终处于迎角保护限幅范围内,见图5。升降舵响应过程稳定,先下降到4.016 5°,再上升到5.117 4°,最后回到配平值,均在升降舵变化限幅范围内,见图6。
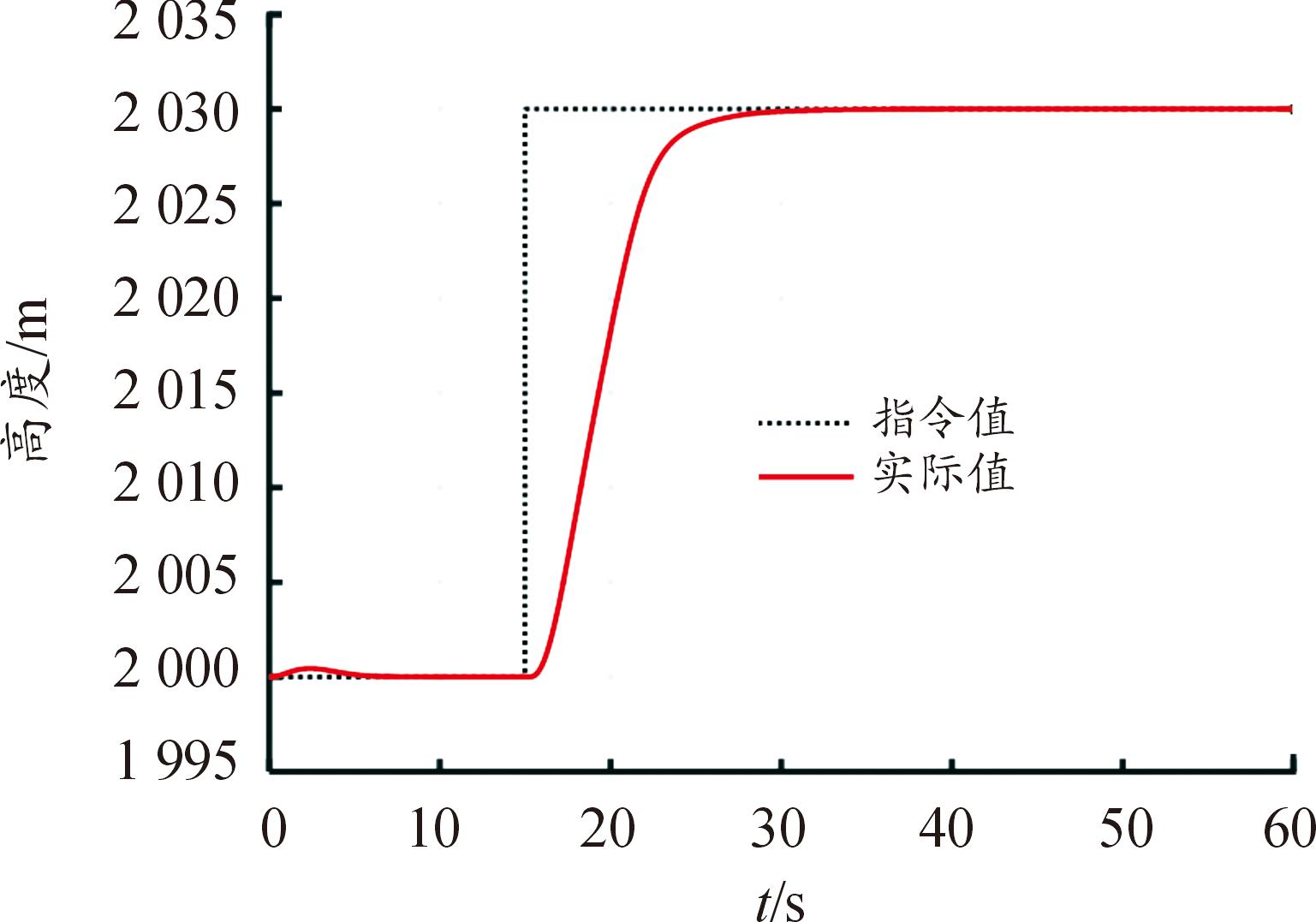
图4 高度响应曲线
Fig.4 Response curve of height
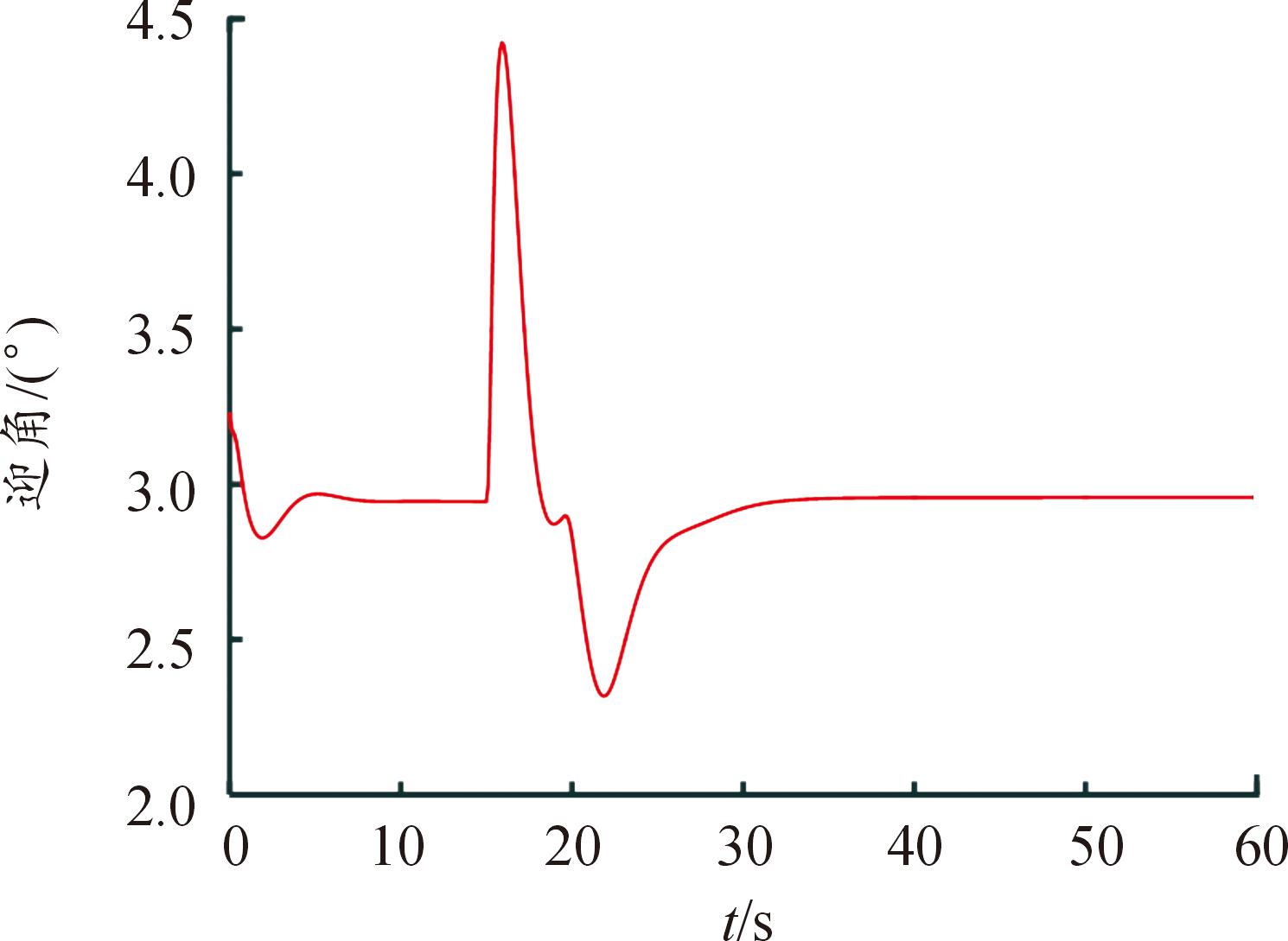
图5 迎角响应曲线
Fig.5 Response curve of angle of attack
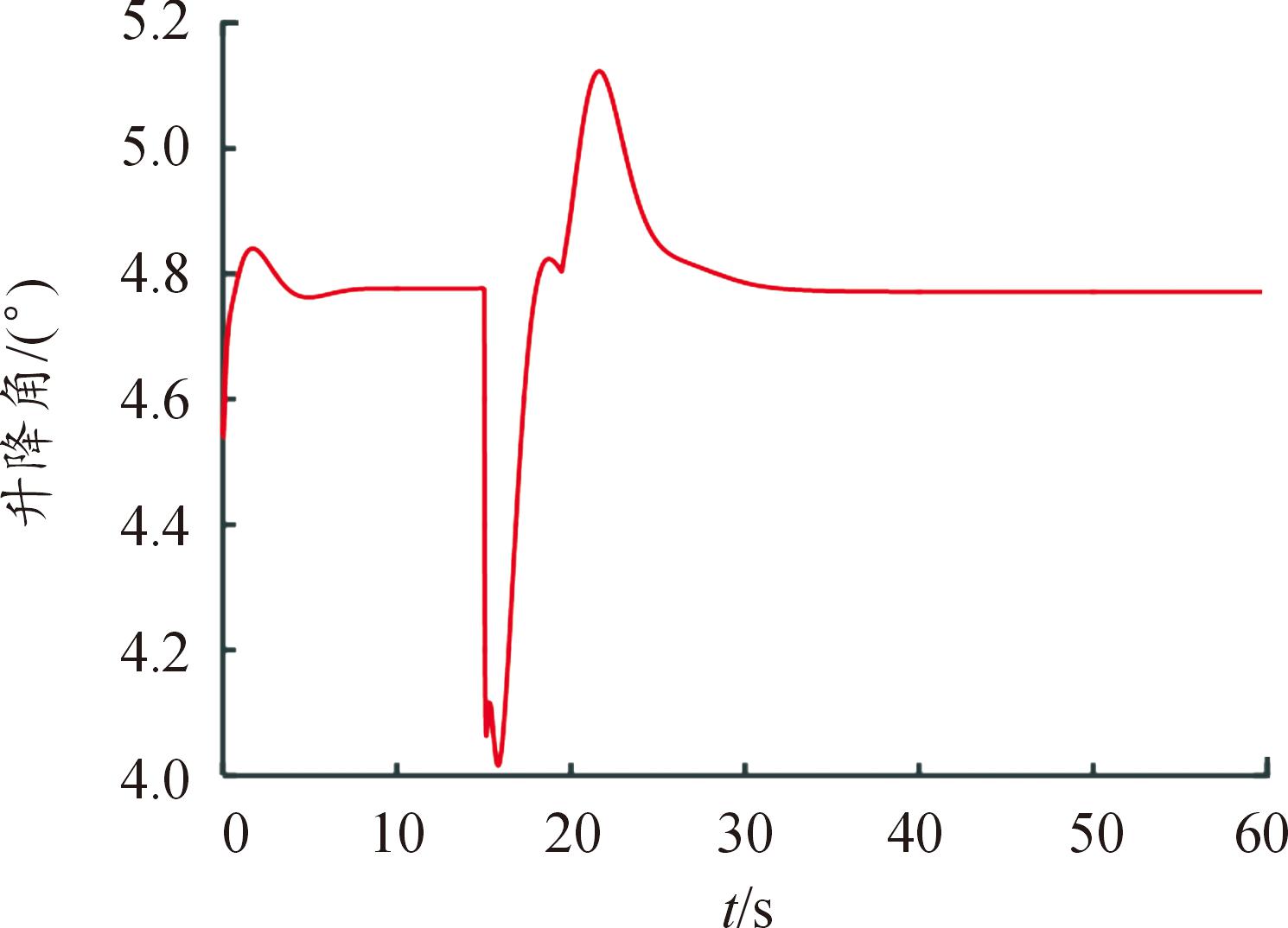
图6 升降舵响应曲线
Fig.6 Response curve of elevator
图7为控制器中LESO对高度控制误差的观测曲线,LESO能够在很短的时间内完成高度误差的观测和跟踪;仿真计算中,在LESO初始状态值设为0(默认值)的情况下,仿真初始阶段没有出现“尖峰效应”。
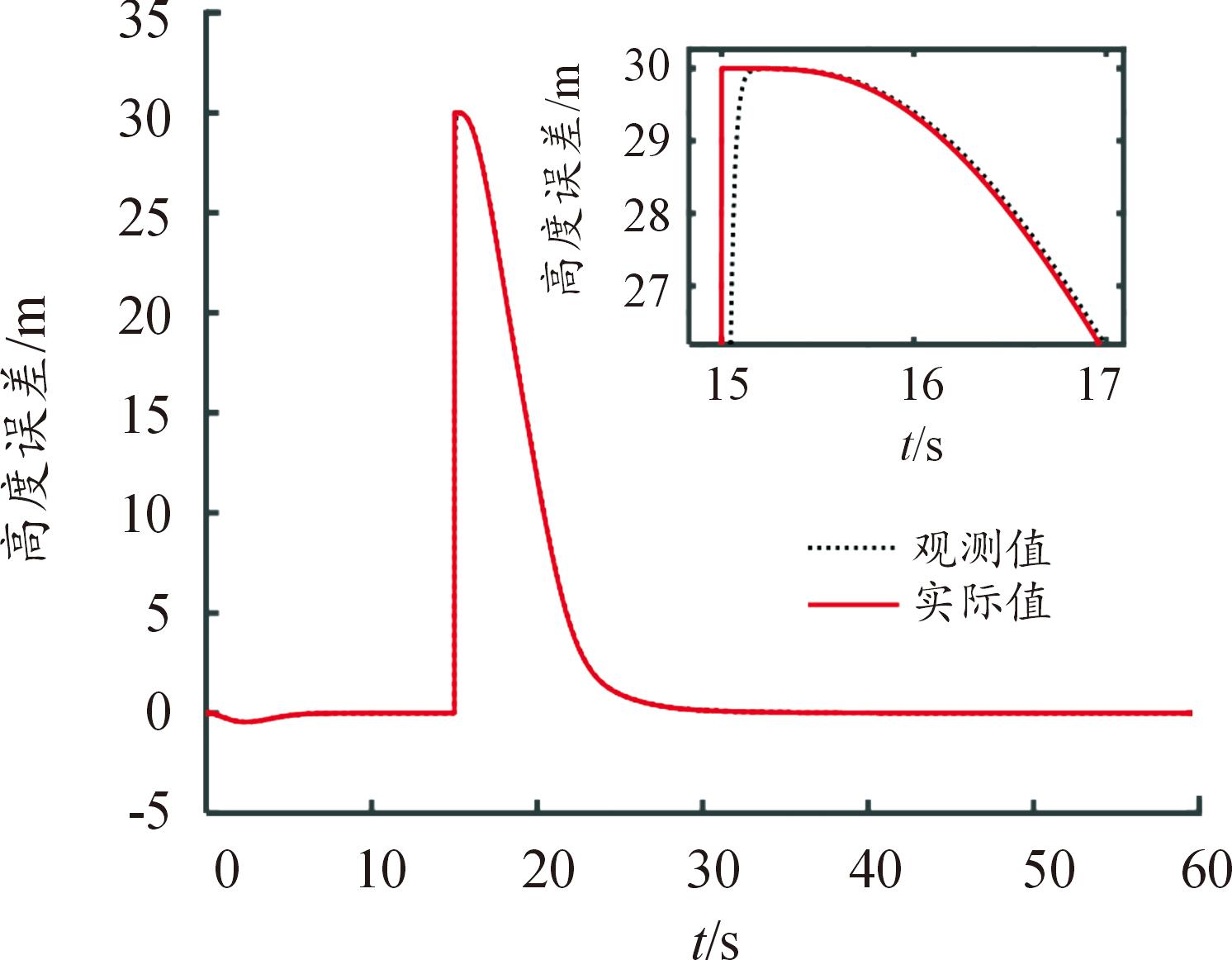
图7 LESO观测值曲线
Fig.7 Observation value curve of LESO
将基于误差的一阶LADRC控制器与基于输出的一阶LADRC控制器进行比较。图8和图9分别为高度阶跃指令下的高度响应对比曲线和升降舵响应对比曲线。基于误差的一阶LADRC比基于输出的一阶LADRC响应过程更加平稳,特别是在接近指令值时没有出现振荡;基于误差的一阶LADRC控制方法中升降舵响应比基于输出的一阶LADRC方法要略微剧烈。此外,基于输出的一阶LADRC高度控制在仿真初始阶段为了避免出现“尖峰效应”,需要将LESO的输出初始状态值设为初始高度。
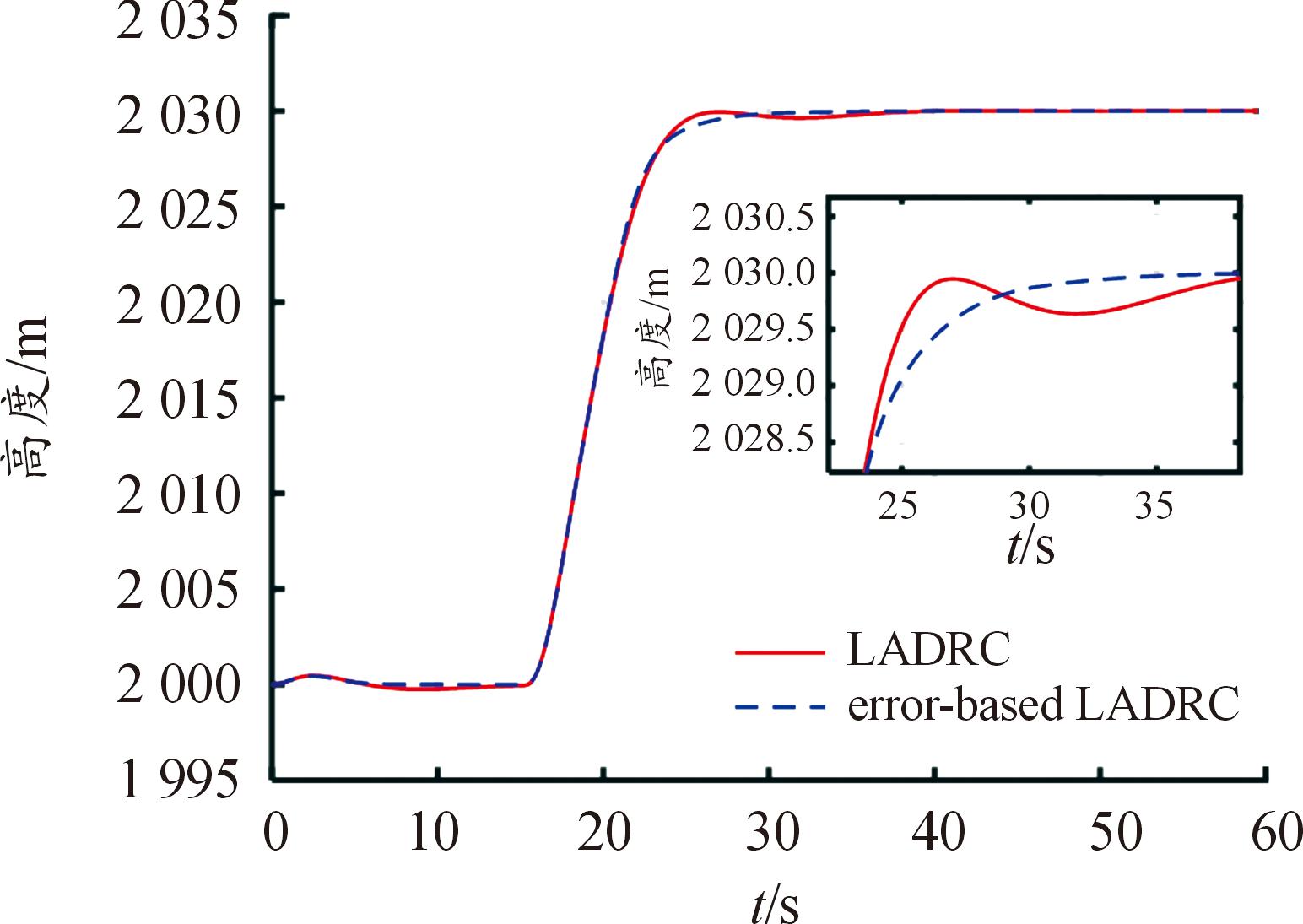
图8 高度响应对比曲线
Fig.8 Comparison curve of height
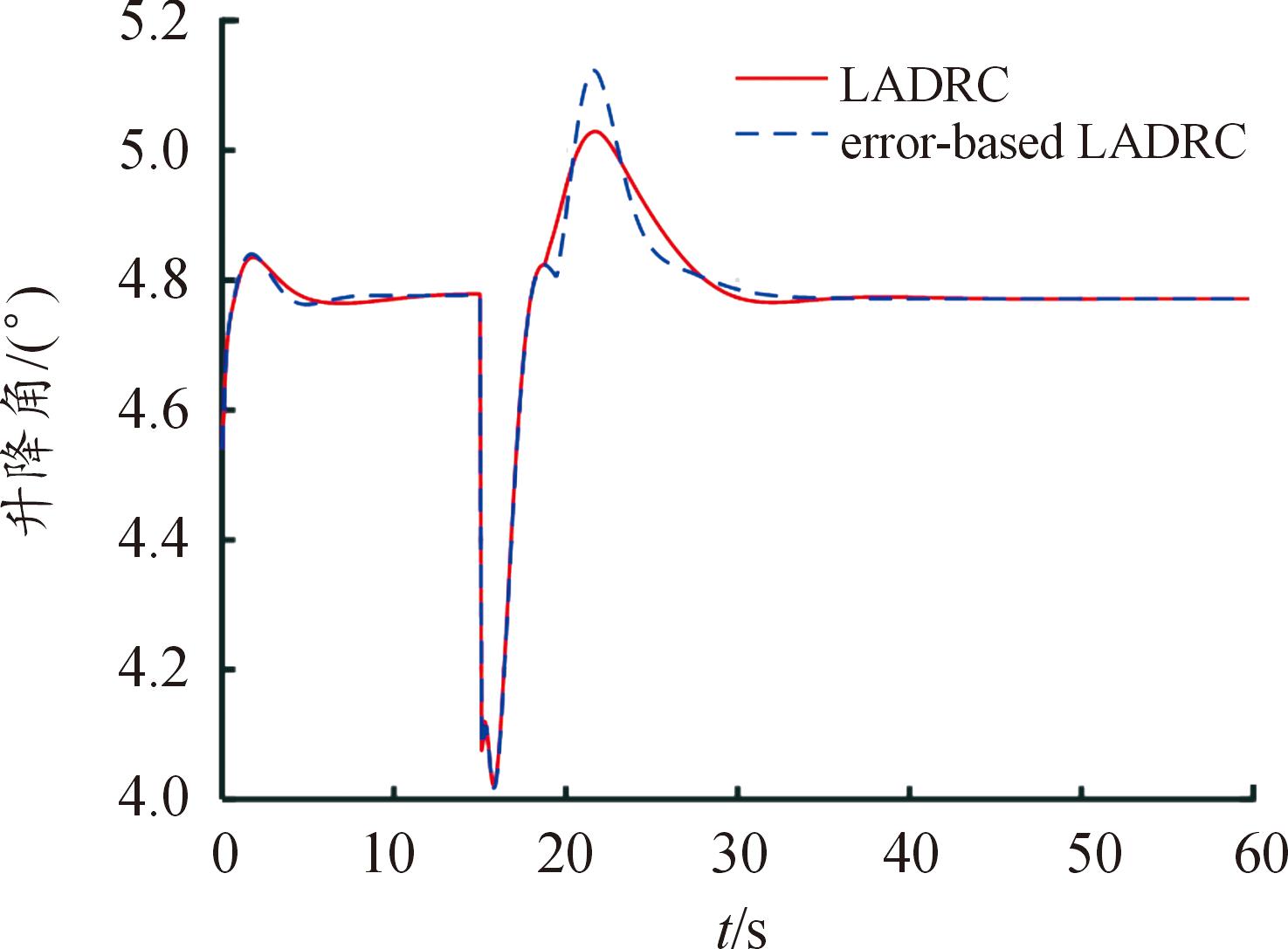
图9 升降舵响应曲线
Fig.9 Comparison curve of elevator
在15~30 s间引入5 m/s的垂直阶跃突风,对比2种方法的高度和升降舵响应,见图10—图11。基于误差的一阶LADRC方法中,垂直风引起的高度响应更加平稳,高度变化的峰值略小,表现出更优良的抗突风干扰性能。
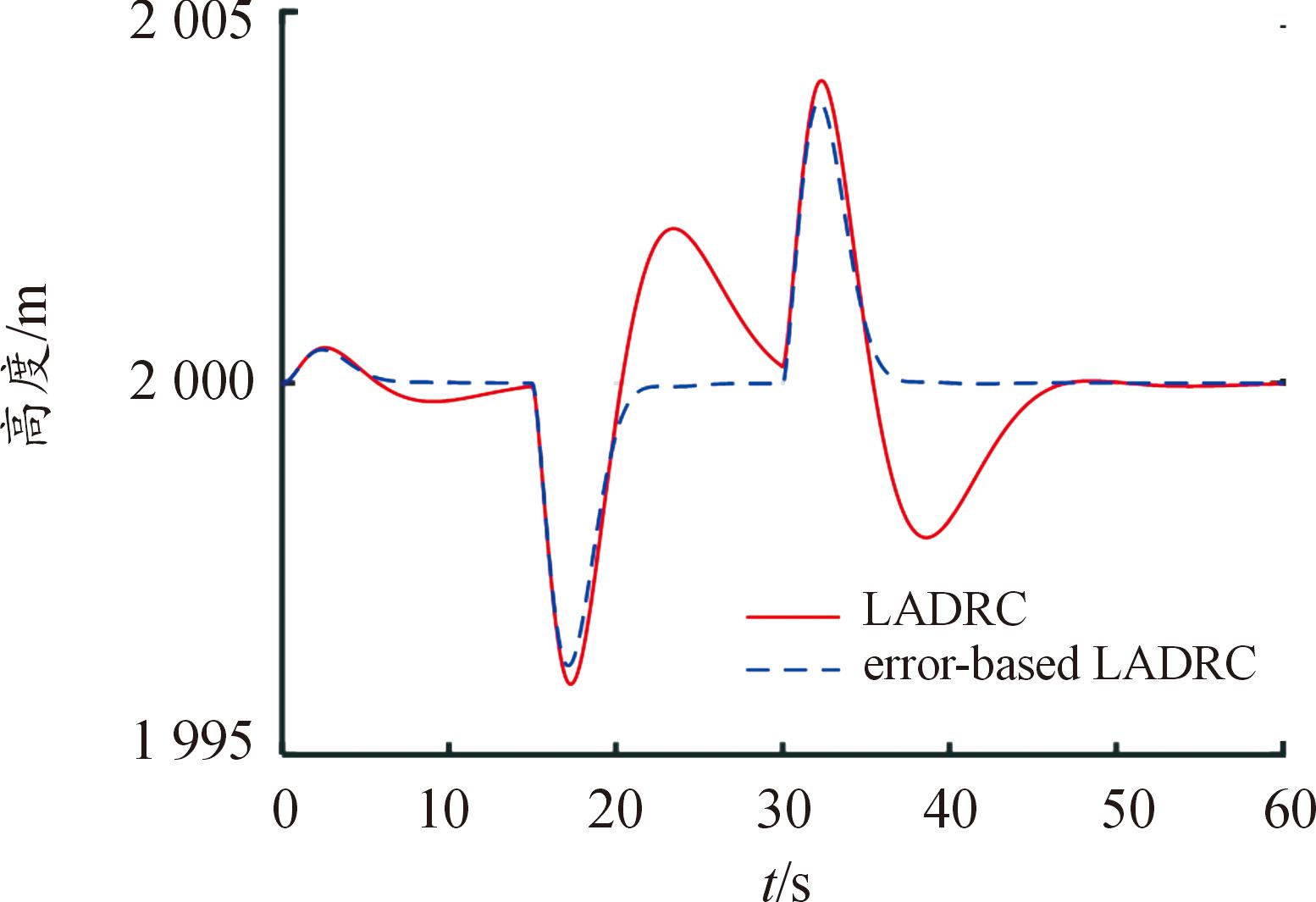
图10 高度响应曲线对比
Fig.10 Comparison curve of height
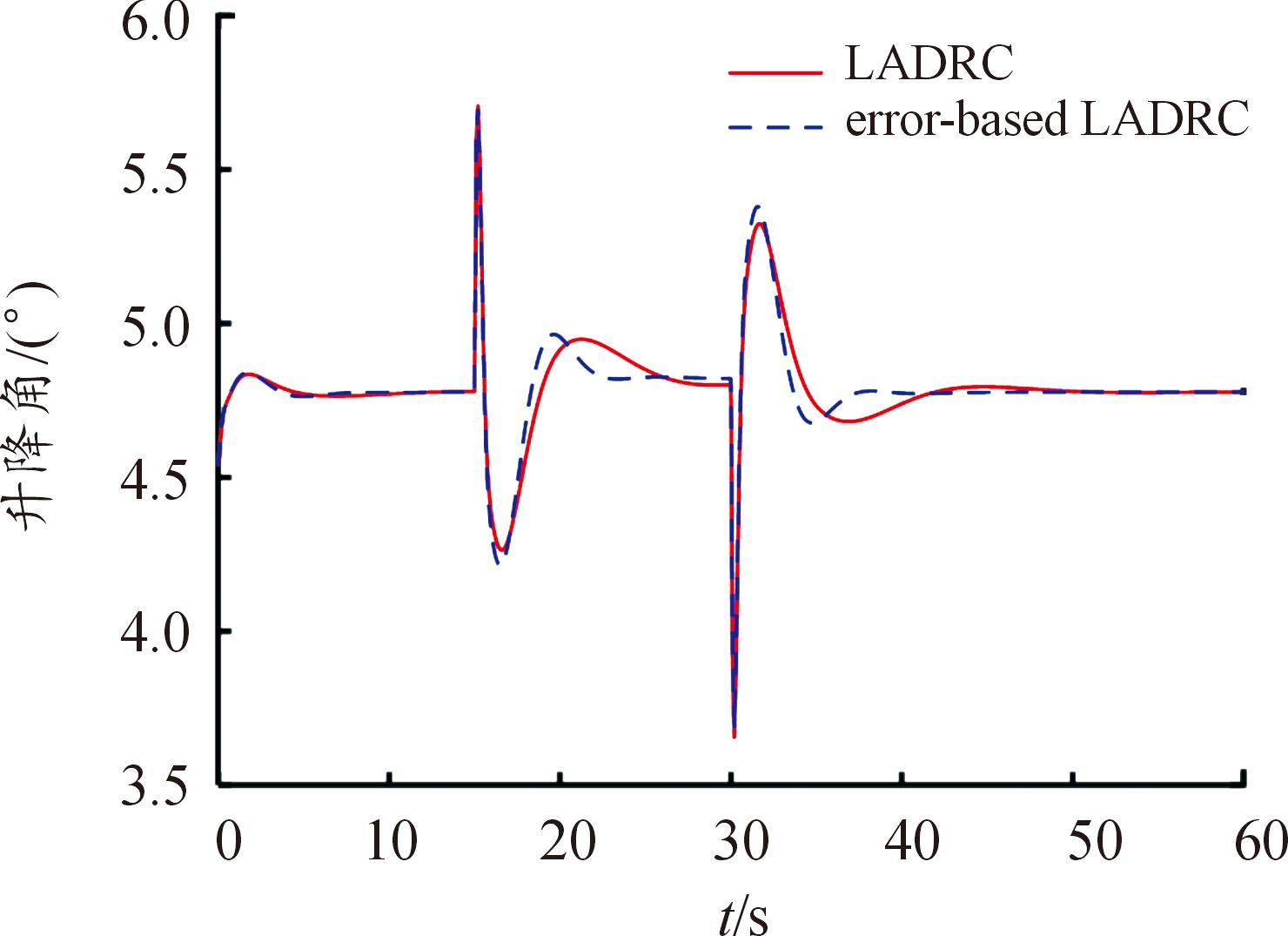
图11 升降舵响应曲线对比
Fig.11 Comparison curve of elevator
4 结论
1) 基于误差的一阶LADRC方法可用于固定翼无人机飞行控制的高度外环控制器设计,能够直接根据高度控制误差信息生成控制输出量,从而简化控制器结构,在无人机采用视觉导航信息进行自主空中对接等场景中具有应用价值。
2) 基于误差的一阶LADRC高度飞行控制器不需要设定LESO的初始状态值就可避免仿真初始阶段的“尖峰效应”。
3) 基于误差的一阶LADRC高度控制比基于输出的一阶LADRC高度控制具有更平稳的动态响应过程和更优良的抗突风干扰性能。
[1] 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2009. HAN Jingqing.Active disturbance rejection control technique-The technique for estimating and compensating the uncertainties[M].Beijing:National Defense Industry Press,2009.
[2] GAO Zhiqiang.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference.Piscataway,NJ:IEEE Press,2003:4989-4996.
[3] 孟晨,张金鹏,林辉,等.基于自抗扰技术的多旋翼姿态控制[J].航空兵器,2020,27(4):33-38. MENG Chen,ZHANG Jinpeng,LIN Hui,et al.Multi-rotor attitude control based on adrc[J].Aero Weaponry,2020,27(4):33-38.
[4] 时来富,沈建新,王启盛,等.四旋翼飞行器的模糊自抗扰姿态控制[J].机械制造与自动化,2021,50(3):157-162. SHI Laifu,SHEN Jianxin,WANG Qisheng,et al.Fuzzy active disturbance rejection attitude control of quadrotor aircraft[J].Machine Building and Automation,2021,50(3):157-162.
[5] 黄正,魏琼,张金姣.三旋翼飞行器建模及自抗扰控制[J].电光与控制,2021,28(6):20-24. HUANG Zheng,WEI Qiong,ZHANG Jinjiao.Trirotor aircraft modeling and active disturbance rejection control[J].Electronics Optics and Control,2021,28(6):20-24.
[6] 高强,刘新鹏,刘春平,等.四旋翼无人机串级自抗扰姿态控制及轨迹跟踪[J].电光与控制,2023,30(3):90-95. GAO Qiang,LIU Xinpeng,LIU Chunping,et al.Cascaded active disturbance rejection attitude control and trajectory tracking of quadrotor UAV[J].Electronics Optics and Control,2023,30(3):90-95.
[7] 赵春明,焦胜海,王晓飞,等.柔性充气空间飞行器姿态控制系统设计[J].兵工学报,2022,43(6):1346-1354. ZHAO Chunming,JIAO Shenghai,WANG Xiaofei,et al.Design of attitude control system for flexible inflatable spacecraft[J].Acta Armamentarii,2022,43(6):1346-1354.
[8] 姜辰,王浩文,李健珂,等.无人直升机自抗扰自适应轨迹跟踪混合控制[J].工程科学学报,2017,39(11):1743-1752. JIANG Chen,WANG Haowen,LI Jianke,et al.Trajectory-tracking hybrid controller based on ADRC and adaptive control forunmanned helicopters[J].Chinese Journal of Engineering,2017,39(11):1743-1752.
[9] 张祥,李广文,曹睿婷,等.基于自抗扰控制方法的自动着陆飞行控制律设计[J].弹箭与制导学报,2020,40(5):98-104. ZHANG Xiang,LI Guangwen,CAO Ruiting,et al.Design for automatic landing flight control law based on active disturbance rejection control method[J].Journal of Projectiles,Rockets,Missiles and Guidance,2020,40(5):98-104.
[10] 高科,宋佳,艾绍洁,等.高超声速飞行器再入段LQR自抗扰控制方法设计[J].宇航学报,2020,41(11):1418-1423. GAO Ke,SONG Jia,AI Shaojie,et al.LQR active disturbance rejection control method design for hypersonic vehicles in reentry phase[J].Journal of Astronautics,2020,41(11):1418-1423.
[11] 罗瑜.基于自抗扰的地效飞行器俯仰控制系统设计[J].电子测量技术,2020,43(6):69-76. LUO Yu.Design of ground effect aircraft pitch control system based on auto disturbance rejection[J].Electronic Measurement Technology,2020,43(6):69-76.
[12] 钟声,黄一,胡锦昌.深空探测航天器姿态的自抗扰控制[J].控制理论与应用,2019,36(12):2028-2034. ZHONG Sheng,HUANG Yi,HU Jinchang.Active disturbance rejection control for attitude control of deep space explorer[J].Control Theory and Applications,2019,36(12):2028-2034.
[13] 安帅.硬式空中加油过程中的受油机飞行控制研究[D].南京:南京航空航天大学,2018. AN Shuai.Research on the flight control of the receiver aircraft in the process of hard aerial refueling[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2018.
[14] 陈志刚,韩维,张勇,等.基于ADRC的舰载机着舰飞行控制系统解耦设计[J].飞行力学,2018,36(1):34-37. CHEN Zhigang,HAN Wei,ZHANG Yong,et al.Decoupling design on aircraft carrier-landing flight control system based on ADRC[J].Flight Dynamics,2018,36(1):34-37.
[15] 吴文海,高阳,王子健,等.基于LADRC的舰载V/STOL飞机短距起飞性能优化[J].航空学报,2019,40(6):131-142. WU Wenhai,GAO Yang,WANG Zijian,et al.Optimization of short take-off performance for carrier-based V/STOL aircraft via LADRC method[J].Acta Aeronauticaet Astronautica Sinica,2019,40(6):131-142.
[16] 户杏启,韩文杰,谭文.一阶线性自抗扰控制的整定[J].信息与控制,2022,51(4):423-432. HU Xingqi,HAN Wenjie,TAN Wen.Tuning of first-order linear active disturbance rejection control[J].Information and Control,2022,51(4):423-432.
[17] MADONSKI R,SHAO S,ZHANG H,et al.General error-based active disturbance rejection control for swift industrial implementations[J].Control Engineering Practice,2019,84:218-229.
[18] CHEN M S,CHEN C C.Robust nonlinear observer for lipschitz nonlinear systems subject to disturbances[J].IEEE Transactions on Automatic Control,2007,52(12):2365-2369.