0 引言
变压器作为高价值的大型电力设备,投资成本可占整个电力行业的60%以上[1]。一旦发生故障,不仅会造成严重的经济损失,更可能危及居民人身安全。如2019年美国纽约一台变压器因继电保护系统缺乏维护且备用系统失效,导致整个城市约5 h用电无法保障[2];2024年山西省侯马市电力变压器因缺乏巡检维护,出现油温异常未及时处理而故障起火,导致6人不同程度的伤亡[3]。
为降低电力系统故障的发生概率并减少事故的产生,需要保持变压器的安全、可靠、经济地运行[4]。而保持变压器的安全、可靠、经济运行的关键前提在于开展电力变压器设备危害性分析,通过对影响电力变压器正常运行的失效模式进行评估与分析,可辨识对电力变压器安全性、可靠性、经济性影响最大的几种失效模式,从而为优化运维策略提供有效参考。
从使用的方法上来看,电力变压器设备危害性分析通常可分为基于故障树的危害性分析、基于设备状态的危害性分析和基于模糊理论的危害性分析[5]。对于基于故障树的危害性分析和基于设备状态的危害性分析,在电力行业中已有相当的研究[6-7]。然而由于电力变压器存在样本获取周期和滞后性较长且失效底事件繁杂等问题,导致基于故障树和设备状态的危害性分析难以推广到更普遍的工程实践中[8]。
与其他方法相比,基于模糊理论的危害性分析因其便捷性和可解释性好,且考虑不确定性因素的优势,使得基于模糊理论的危害性分析在电力变压器中得以广泛研究。Guo等[9]提出了一种基于故障模式的变压器可靠性分析和运维策略研究方法,将贝叶斯方法与风险优先数结合,实现小样本下维修资源的分配优化。Eyü
等[10]将老化因素纳入整个评估过程中,细分故障标准评估,以更准确地预测故障并对故障处理优先级进行排序。Minglin等[11]则提出一种基于直觉模糊偏好选择指数方法的电力变压器部件风险优先级评估方法,找出电力变压器故障的原因,降低电力变压器部件的故障率。Yu等[12]则提出一种基于三参数区间灰数决策的电力变压器风险评估方法,采用Nataf变换和Cholesky分解消除随机变量的相关性,基于消除相关性的随机变量来考虑各失效模式对电力变压器的影响。Park等[13]考虑不确定因素对变压器的影响,结合等效年均成本,分析和优化了电力变压器的经济更换周期。张博等[14]结合模糊理论和证据理论对变压器进行绝缘状态评估,实现了变压器矛盾状态信息的消除。邹国惠等[15]使用模糊层次分析法对变压器知识图谱进行分析,有效分析出变压器风险的同时大大降低了电力变压器的故障漏检率。
调研发现现有研究主要集中于围绕变压器的特定部件或者一个单元展开。以往的失效危害性分析,多以围绕设备单元展开的失效模式列举说明为主,缺少对失效模式主体性的强调和对成本影响的重视[5]。
针对上述问题,本文以变压器失效模式为研究主体,运用模糊集理论综合评估现有的缺陷记录,使用独立考虑运行维护成本的风险分析优先数法对失效危害性进行分析,同时使用网络分析法进一步细化风险优先数法中的严酷度等级评定。通过精确识别和评价失效风险,优化维护策略,降低成本,为电力系统的风险管理提供了新的技术手段。
本文的主要贡献和创新点可总结为以下几点:
1) 采用模糊集理论,将确定的缺陷记录与不确定的模糊经验语言相结合,共同确定变压器不同失效模型下的失效概率,实现缺陷记录数据与先验知识的融合,提高失效概率评估的可信度;
2) 使用网络分析法综合考虑电力变压器各影响因素之间相互影响的强耦合关联,细化严酷度等级评定,实现对电力变压器危害的复合关联风险评估;
3) 扩充风险分析维度,在风险分析中独立考虑运行和维护成本,提高成本关注度,使得风险评估要素更加全面。
1 方法过程
如图1所示,本方法以变压器失效模式为核心研究对象,旨在对其失效危害性进行分析,得出维修资源分配的参考意见。基于模糊集理论(fuzzy set theory,FZT),将收集到的缺陷记录数据与专家经验语言相结合,计算出变压器不同失效模式下的失效概率。接着将失效概率与其他需要考虑的外部风险因素,如严酷度、检测难度、运维成本等要素一起共同构成风险优先数(risk priority number,RPN)方法中的风险量化依据。并引入网络分析法(analytic network process,ANP),以评估变压器中人员伤害、设备损坏、环境危害和任务失败等各后果决策要素及其状态事件间的相互联系和影响,提升风险评估的精确性。
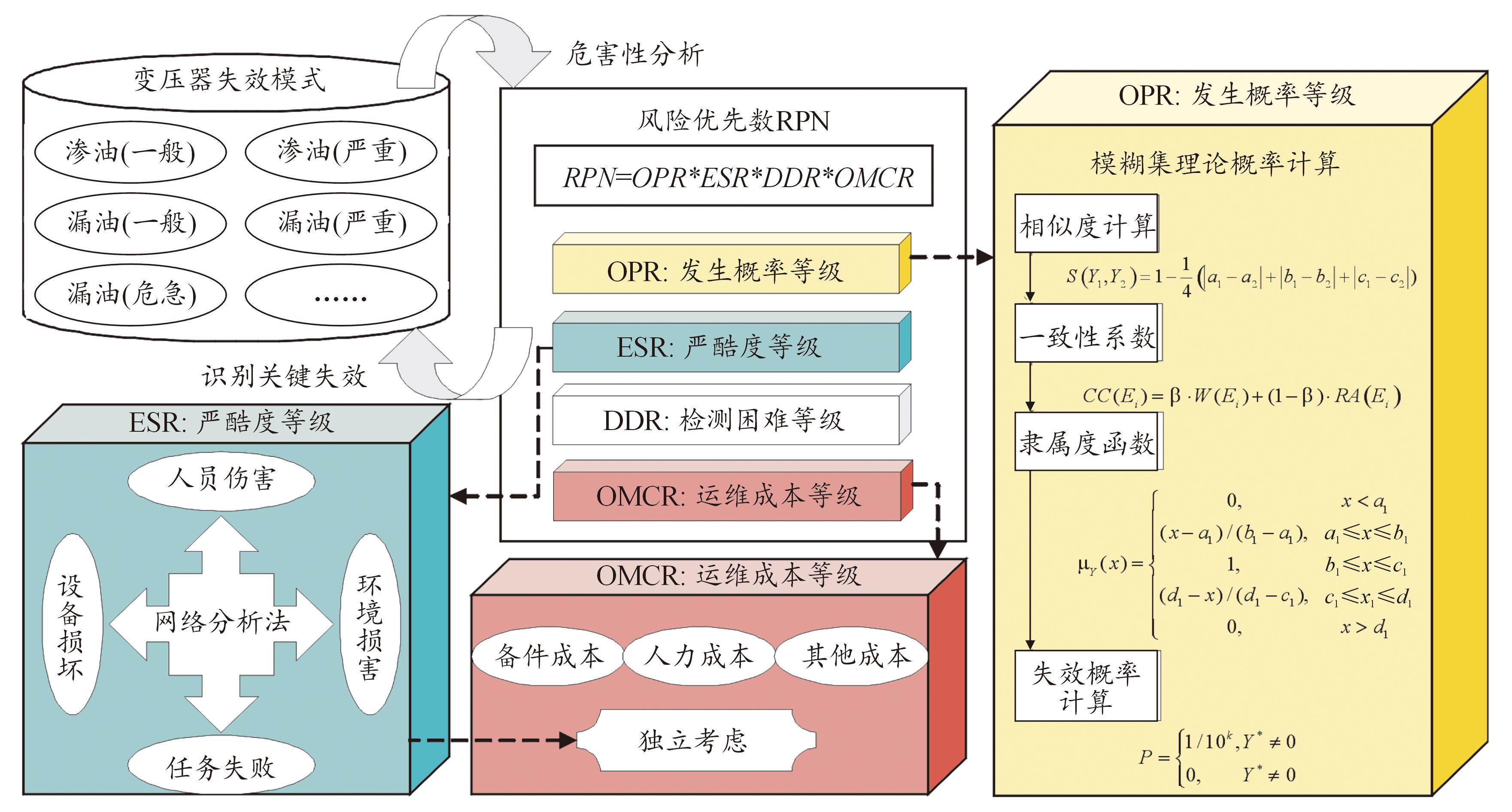
图1 总体框架图
Fig.1 Overall framework
1.1 变压器失效模式分类
220 kV油浸式变压器主要有本体、套管、有载分接开关、非电量保护和冷却系统等部件[16]。参照IEC 60422中关于电力变压器油品质量评估的技术要求,对这些部件分别从渗油、漏油和锈蚀3种常见失效模式进行分类整理。并依据IEC 60599中失效等级划分,根据失效严重程度进行一般、严重和危急3种程度的评级,从而建立起标准化的故障诊断与评估体系,便于后续计算与分析。
1.2 基于模糊集理论的失效概率计算
采用模糊集理论将语言值转化为模糊数,以确定失效模式概率,作为风险优先数中发生概率等级的评估依据[17]。本方法选择梯形模糊数将专家的语言值转换为模糊数。模糊数是由值范围为[0,1]的向量(a,b,c,d)构成。挑选7种模糊术语,包括非常低(very low,VL)、低(low,L)、相当低(fewer low,FL)、中等(middle,M)、相当高(fewer high,FH)、高(high,H)和非常高(very high,VH)启发专家判断。具体梯形模糊数的语言值和相应模糊数的映射关系如表1所示。
表1 梯形模糊数与对应的风险评分
Table 1 Trapezoidal fuzzy numbers and corresponding risk scores
语言值模糊数非常低(VL)(0,0,0.1,0.2)低(L)(0.1,0.2,0.2,0.3)相当低(FL)(0.2,0.3,0.4,0.5)中等(M)(0.4,0.5,0.5,0.6)相当高(FH)(0.5,0.6,0.7,0.8)高(H)(0.7,0.8,0.8,0.9)非常高(VH)(0.8,0.9,1,1)
基于表1赋予专家资质权重,具体计算如下[18]:
(1)
式中: W(Si)为专家i的权重S分数。具体权重分配基于GB/T 24353—2022风险管理中对专家等人员的风险评价说明,从教育水平、工作年限、职称和年龄4个维度对专家资质背景进行综合评估。具体权重分配说明如表2所所示。
表2 专家背景因素和权重分数
Table 2 Expert background factors and weight scores
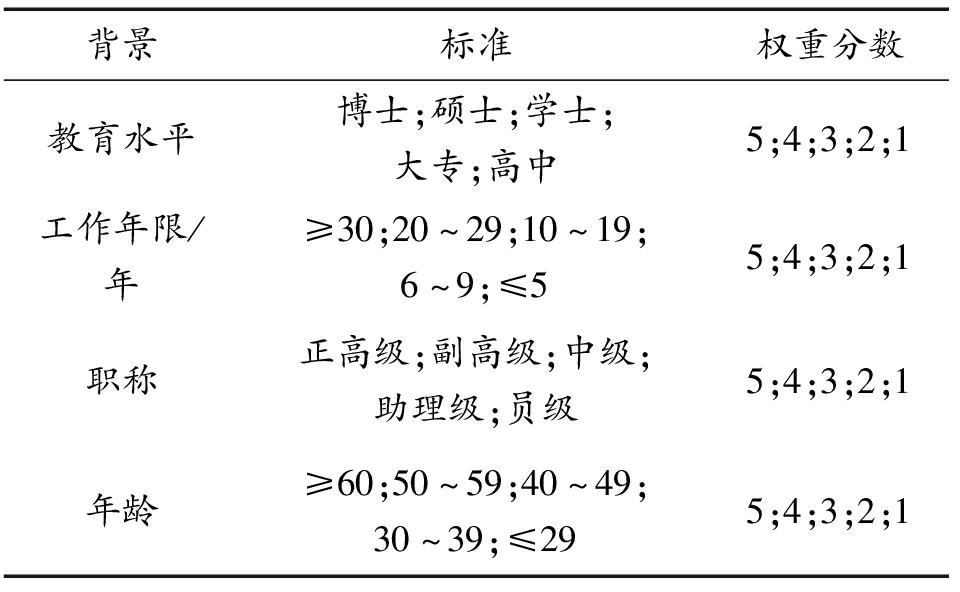
背景标准权重分数教育水平博士;硕士;学士;大专;高中5;4;3;2;1工作年限/年≥30;20～29;10～19;6～9;≤55;4;3;2;1职称正高级;副高级;中级;助理级;员级5;4;3;2;1年龄≥60;50～59;40～49;30～39;≤295;4;3;2;1
由于不同专家对同一事件有不同判断。考虑专家意见一致性,利用线性关系聚合,采用相似性聚合方法(similarity aggregation method,SAM)综合不同专家对相同因素的判断。由于SAM忽视了不同专家间的权重大小以及判断相似度的相互依赖影响,因此为获得准确概率值,提出改进SAM以聚合专家权重进行一致性计算。
设每个专家Ei(i=1,2,…,n)对相同事件Xj(j=1,2,…,n)所给定语言值被转换为相应模糊数Yi=(ai,bi,ci,di)。假设Y1=(a1,b1,c1,d1)和Y2=(a2,b2,c2,d2)为专家E1和E2给出的判断后所对应的梯形模糊数。计算模糊数Y1和Y2的相似度S(Y1,Y2):
(2)
式中: S(Y1,Y2)∈[0,1],S(Y1,Y2)为专家E1和E2判断的一致性。
基于式(1)的专家资质权重和式(2)所计算的相似度S(Y1,Y2),可计算专家Ei判断的加权一致性(weighted agreement,WA)和相对一致性(relative agreement,RA):
(3)
(4)
将式(1)的专家资质权重与式(4)进行结合,计算一致性系数(consensus coefficient,CC):
CC(Ei)=β·W(Ei)+(1-β)·RA(Ei)
(5)
式中, β∈[0,1]是一个松弛因子,表示专家资质对其判断的一致性影响。在本方法中,β=0.5表示专家资质和判断的一致程度对事件权重赋值同等重要。
聚合不同专家对相同事件的判断,相应的集合模糊数YAG为
YAG=CC(E1)·Y1+CC2·Y2+…+CC(Ei)·Yi
(6)
其中,Yi=(ai,bi,ci,di)是一个梯形模糊数,其隶属函数为
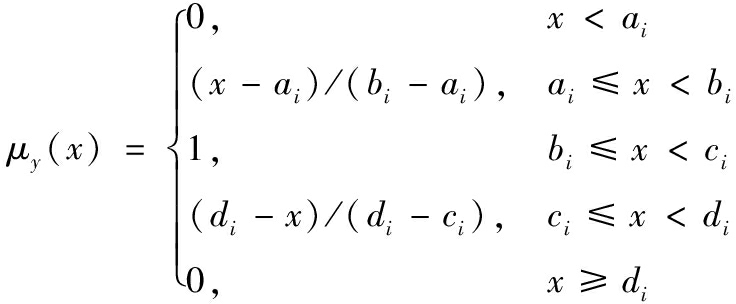
(7)
由于最终的聚合结果YAG为模糊数,不能直接用于风险分析。为获得精确概率值,采用区域中心(center of area,CoA)对聚合模糊数进行去模糊:
(8)
对于梯形模糊数,去模糊化公式可被修改为
(9)
事件失效概率P可通过如下公式获得:
(10)
式中,k为缩放因子,可将模糊推理的结果合理地映射到[0,1]区间的概率值[19],满足:
k=2.301×[(1-Y*)/Y*]1/3
(11)
1.3 基于网络分析法的严酷度等级计算
层次分析法(analytical hierarchy process,AHP)是一种广泛应用的决策分析方法,通过构造判断矩阵计算指标权重来评估方案的优劣[19]。由于AHP方法对各风险要素的分析存在独立性假设,难以对以变压器为代表的大型设备进行耦合关联分析[20]。而与AHP相比,网络分析法(analytic network process,ANP)通过引入超矩阵的概念,采用多元非线性层次结构,不仅考虑了各因素之间的相互影响和反馈机制,还丰富了权重的内涵[21]。ANP可将单一的线性层次结构转化为更加复杂和真实的网络结构,从而提供了一种更加全面和精确的指标权重计算方法。因此本文基于ANP对电力变压器进行复合网络关联分析。具体而言,使用ANP方法的基本步骤如下:
1) 建立ANP网络结构
ANP方法将一个具体的问题简化为2个层次:控制层和网络层。对于某一具体目标或决策方案来说,在考虑控制层各准则权重时,应当将控制层各准则赋予独立性,采用AHP方法获取各准则权重。控制层各准则下有许多可支配元素,这些元素可以相互作用影响,具备反馈机制,元素间不独立。
对于风险优先数中的严酷度等级来说,在对失效影响的严重程度进行判定时,考虑的因素是多样的。根据ISO31000—2009的相关规定,决策风险的主要成分应当至少包含所明确组织的风险管理目标、确保风险管理活动顺利进行的人力资源要素、具体风险后果及其严重程度以及任务外部的环境要素影响[22]。通过建立任务目标,识别潜在风险源,分析风险源性质及其严重程度来进行控制层建模;通过对控制层的潜在风险源分解与网络联立实现网络层建模。
基于ISO31000—2009的风险管理流程,结合电力行业相关专家经验,以失效严酷度等级作为总评估目标,以保证人员与环境安全和提高电力变压器运维质量和效率为原则,可得出电力变压器巡检维护风险在ANP控制层中的四大要素,即人员伤害,设备损坏,任务失败和环境损害。
将总目标和4个准则结合来构成控制层后,分别从人员伤害,设备损坏,任务失败和环境损害4个准则角度进行网络层分析。在ANP的网络层中,人员伤害准则下包含人员安全意识和人员技能水平2个元素,设备损坏准则下包含设备质量和运行状态两个元素,任务失败准则下包含任务难度和任务急切程度两个元素,环境损害准则下包含工作环境一个元素,这些元素构成了网络层。建立的失效严酷度等级ANP网络结构如图2所示。
图2 网络结构
Fig.2 Network structure diagram
2) 采用1～9标度法建立未加权超矩阵[23];
3) 建立加权超矩阵;
4) 计算相对权重。
1.4 基于风险优先数法的综合风险量化
风险优先数(risk priority number,RPN)是故障模式与影响分析(failure mode and effect analysis,FMEA)中用于量化风险的一种工具[15]。它通过评估发生概率(occurrence probability ranking,OPR)、影响严酷度等级(effect severity ranking,ESR)和检测难度等级(detection difficulty ranking,DDR)3个因素等级来计算每个失效的风险程度[24]。基于RPN计算结果,可以判断关键失效模式和非关键失效模式,合理分配维修保障资源,提高设备整体的可靠性和安全性。计算公式如下[25]:
RPN=OPR×ESR×DDR
发生概率等级OPR用于评定某个失效模式实际发生的可能性。图3给出了OPR的评分准则,失效模式在产品的寿命周期内发生的概率对应着不同的评分等级。
图3 OPR评分准则图
Fig.3 OPR scoring criteria chart
严酷度等级ESR用于评定所分析的故障模式的最终影响的程度。表3给出了ESR的评分准则,用于反映失效对人员安全、设备完整性和环境影响的综合考量。评分等级从轻度到灾难性,逐步加重,有助于区分不同程度的风险影响,从而优先处理最严重的问题。
表3 ESR评分准则表
Table 3 ESR scoring criteria chart
ESR评分等级严酷度等级失效影响的严重程度1、2、3轻度的不足以导致人员伤害、设备轻度的损坏及轻度环境损坏,但它会导致非计划性维护或修理。4、5、6中等的导致人员中等程度伤害、设备中等程度损坏、任务延误或降级及中等程度环境损害。7、8致命的导致人员严重伤害、设备严重损坏、任务失败及严重环境损害。9、10灾难的导致人员死亡、设备毁坏和重大环境损害。
检测困难等级DDR用于评定所分析的故障模式能够被检测出来的困难程度。表4给出了DDR的评分准则。该准则考虑了故障模式的可检测性。从容易检测到极难检测,反映了发现潜在问题的难度。有助于识别那些难以察觉但可能造成严重后果的隐患,促使组织加强对难以检测问题的监控和预防。
表4 DDR评分准则表
Table 4 DDR scoring criteria chart
ESR评分等级严酷度等级失效影响的严重程度1、2极易被检测失效模式非常容易被识别和检测到,使用标准检测方法或在正常操作过程中就能立即发现这些失效。3、4、5易被检测失效模式相对容易被检测到,可能需要一些基本的测试或检查流程,但通常不需要高度专业化的工具或知识。6、7、8难被检测失效模式较难被检测出来,可能需要特殊的测试设备、详细的诊断程序或特定的技术知识。9、10极难被检测失效模式极其难以被检测到,即使使用高级的测试和诊断方法也可能无法准确识别。
考虑到变压器实际运行和维护工作中的情况,本论文结合运行和维护历史成本数据,创新性地在风险优先数法中加入对运行和维护成本的单独分析。在原先的方法中,运行和维护成本被作为影响严酷度等级评分准则当中的一个因素去考虑。在这种情况下,运行和维护成本对于失效模式的影响被明显低估了,因此为了突出成本的重要性,在风险优先数法中加入对运行和维护成本等级(operation and maintenance costs ranking,OMCR)的单独考虑。更新后的RPN*计算公式为
RPN*=OPR×ESR×DDR×OMCR
(13)
运行和维护成本等级OMCR用于评定变压器某失效模式发生后所造成的运行和维护成本。运行和维护成本一般包含维修备件成本、人力成本以及失效带来的其他成本。运行和维护成本越低的失效模式评分越低,图4给出了OMCR的评分准则。
图4 OMCR评分准则图
Fig.4 OMCR scoring criteria chart
2 案例
本文中选取220 kV油浸式变压器为案例,对其进行失效危害性分析。220 kV油浸式变压器是一种高压电力变压器,主要用于传输线路中进行电压的转换,即将较高电压级的电能降低到较低电压级,以便在城市电网和大型工业设施中使用。由于其工作电压级别较高,这类变压器具有特殊的设计和安全要求。220 kV变压器使用绝缘油来进行冷却和绝缘。油不仅有效地传递内部产生的热量到变压器外壳及外部冷却系统,还提供电气绝缘以防止短路和电气故障。图5是220 kV油浸式变压器的现场实拍图。具体风险优先数量化评估过程如下:
图5 变压器实拍图
Fig.5 Transformer actual photo
2.1 模糊危害网络风险优先数分析流程
2.1.1 发生概率等级的计算及分析
选取7名专家E1～E7,经过表1和表2的评分表格可对专家的资历信息进行权重转换,专家的评分权重如表5所示。
表5 专家资质评分及其权重表
Table 5 Expert qualification rating and weight table
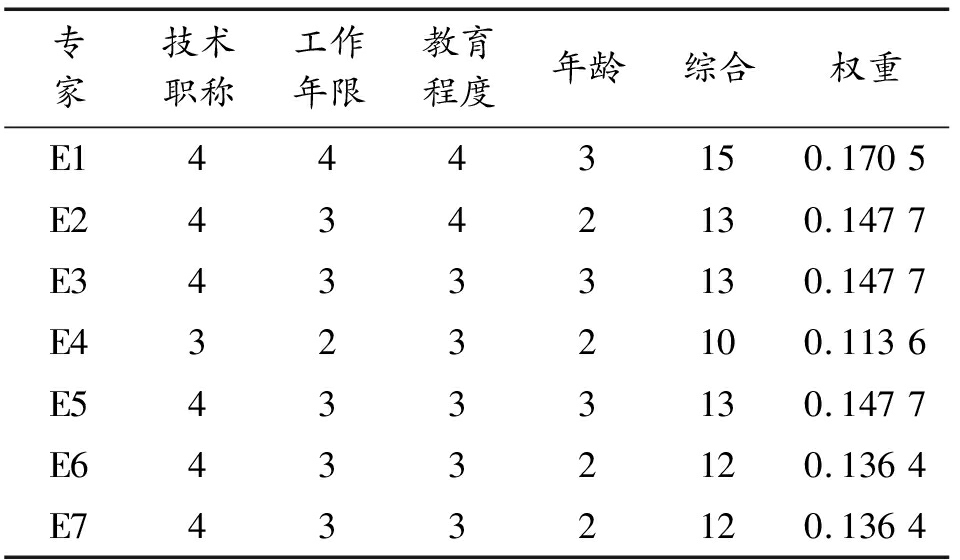
专家技术职称工作年限教育程度年龄综合权重E14443150.1705E24342130.1477E34333130.1477E43232100.1136E54333130.1477E64332120.1364E74332120.1364
选取变压器油箱和储油柜的渗油和漏油缺陷为案例进行分析。基于表5的专家权重信息,将现场巡检所得的变压器缺陷记录数据结合起来,运用式(9)与式(10)的模糊数转化,实现模糊语言到失效概率的转化,转化的相关过程及其结果数据如表 6所示。所得变压器大修年限内各失效模式的发生概率如表6所示。
表6 变压器模糊失效概率转化表
Table 6 Fuzzy failure probability conversion table for transformers
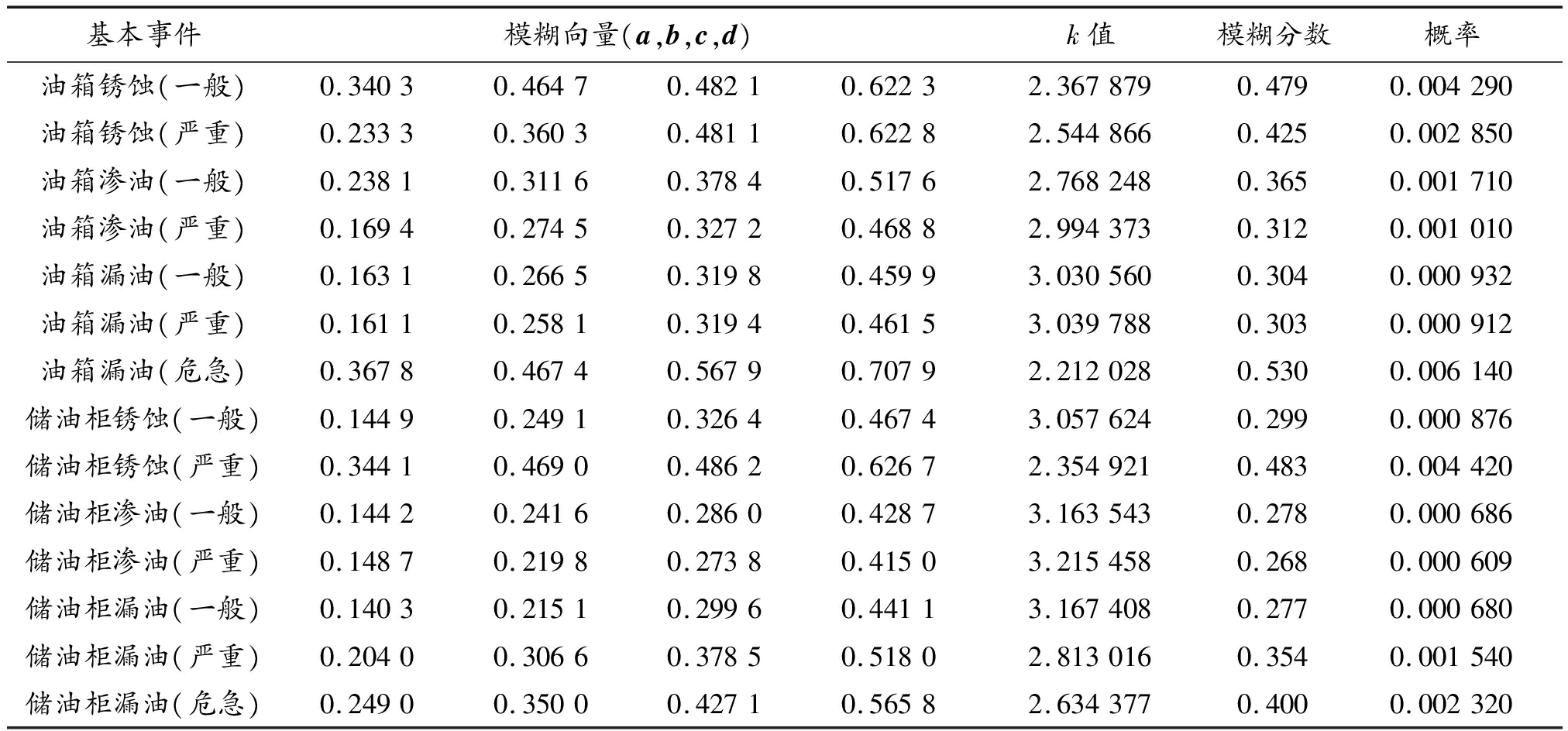
基本事件模糊向量(a,b,c,d)k值模糊分数概率油箱锈蚀(一般)0.34030.46470.48210.62232.3678790.4790.004290油箱锈蚀(严重)0.23330.36030.48110.62282.5448660.4250.002850油箱渗油(一般)0.23810.31160.37840.51762.7682480.3650.001710油箱渗油(严重)0.16940.27450.32720.46882.9943730.3120.001010油箱漏油(一般)0.16310.26650.31980.45993.0305600.3040.000932油箱漏油(严重)0.16110.25810.31940.46153.0397880.3030.000912油箱漏油(危急)0.36780.46740.56790.70792.2120280.5300.006140储油柜锈蚀(一般)0.14490.24910.32640.46743.0576240.2990.000876储油柜锈蚀(严重)0.34410.46900.48620.62672.3549210.4830.004420储油柜渗油(一般)0.14420.24160.28600.42873.1635430.2780.000686储油柜渗油(严重)0.14870.21980.27380.41503.2154580.2680.000609储油柜漏油(一般)0.14030.21510.29960.44113.1674080.2770.000680储油柜漏油(严重)0.20400.30660.37850.51802.8130160.3540.001540储油柜漏油(危急)0.24900.35000.42710.56582.6343770.4000.002320
基于图6失效概率结果图的发生概率,结合图 3所绘制的发生概率评分准则,各失效模式下的等级为7、7、7、6、6、6、7、6、7、6、6、6、7、7。结合图 6的发生概率及其转化所得的失效模式等级可知,作为常见失效模式,漏油和锈蚀在变压器油箱和储油柜两个部件中的发生概率较高,且高于发生概率0.001的失效模式多为一些部件的严重乃至危急类型,例如油箱漏油(危急)、储油柜锈蚀(严重)、油箱锈蚀(严重)、储油柜漏油(严重)、油箱渗油(严重)等。
图6 失效概率结果图
Fig.6 Failure probability result chart
2.1.2 严酷度等级的计算及分析
基于图2所构建的电力变压器严酷度等级网络分析架构,将各风险要素分别进行两两评估比较,以此确立各要素间的重要程度对比。如图7所示,以人员伤害和其他控制层要素的评估为例,基于各专家先验知识,设定人员伤害因素为最高权重(4～7分范围),任务失败次之(3～5分范围),环境损害的相对重要性最低(2～3分范围)。而设备损害则比环境损害略微重要。
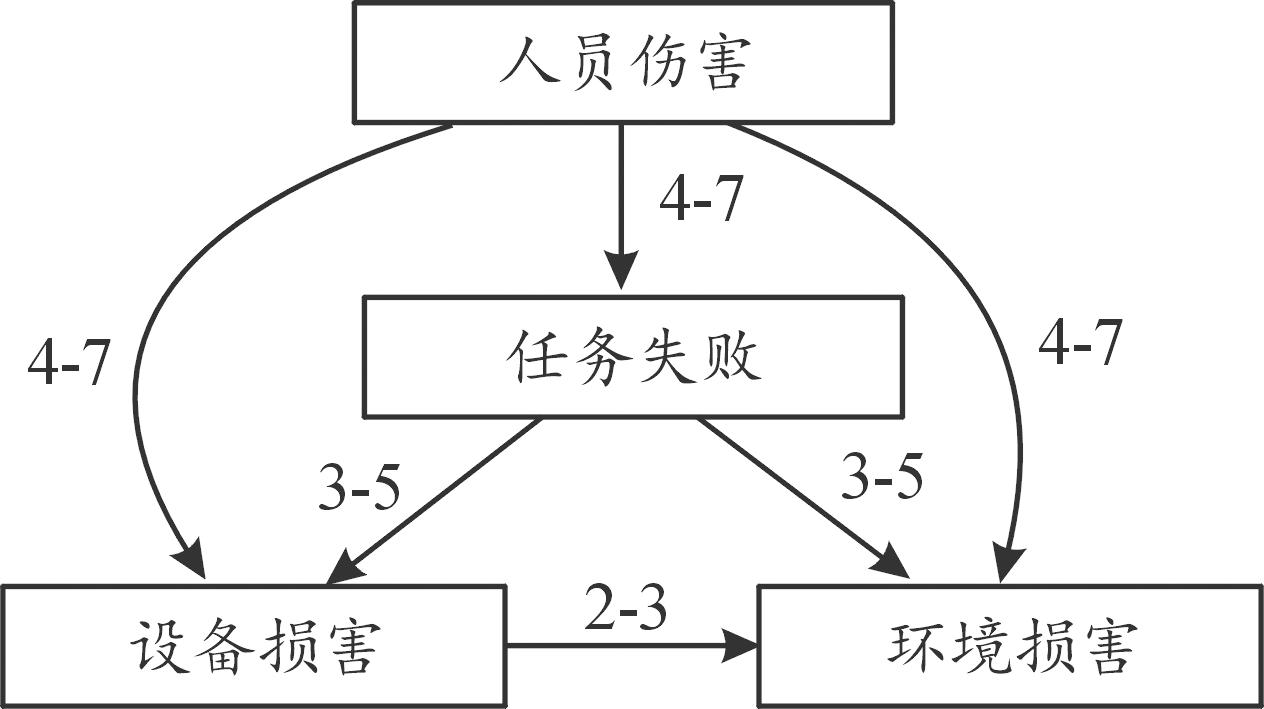
图7 两两比较图
Fig.7 Pairwise comparison diagram
对加权超矩阵进行归一化处理后可以得到各准则和准则下各影响因素的相对权重。使用Super Decisions软件进行计算后可得到各影响因素的权重,其结果如图8所示。通过图8的结果可知,在严酷度等级的评价中,人员伤害的权重远高于其他因素,占比超过60%。任务失败的权重约为24%,虽然显著低于人员伤害,但仍然是第二重要的考虑因素,表明在确保人员安全的前提下,影响电力变压器维修风险的最主要因素是维修任务的失败情况。设备损坏和环境损害的权重相对较低,但仍然不可忽视。特别是设备损坏(8.4%)略高于环境损害(6.9%),反映了电力变压器设备本身对严酷度等级影响较大。
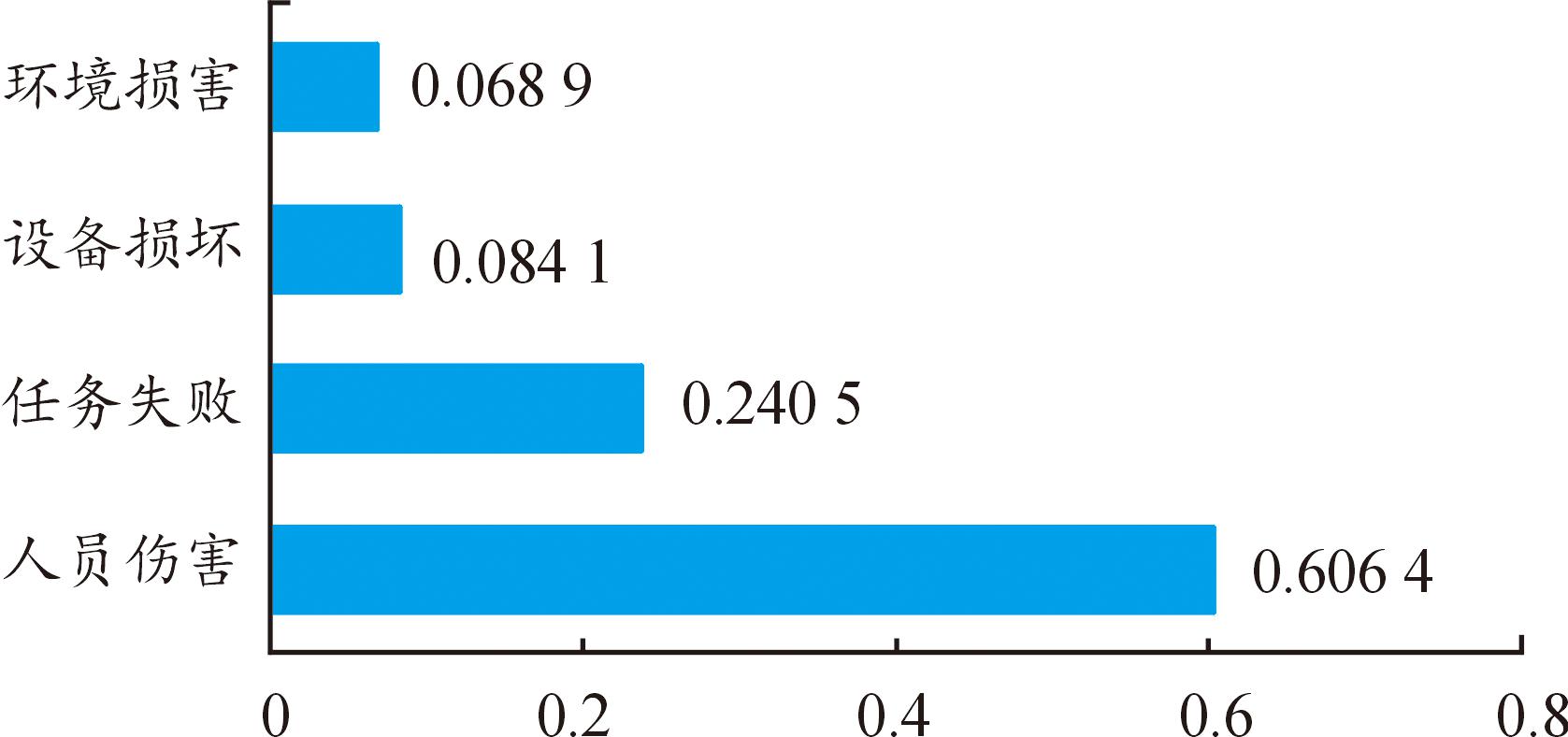
图8 权重计算结果图
Fig.8 Weight calculation result chart
2.1.3 检测难度等级及其运维成本等级的计算及分析
检测难度等级以及其运维成本等级由内蒙古电力公司相关专家依据实际情况结合工程经验依照评判标准给出。各失效模式的检测困难等级分别为3、2、3、2、3、3、2、4、3、4、3、4、4、3,运维成本等级为1、1、1、1、1、1、7、1、1、1、1、1、1、7。
在进行ESR评分时,需要先对四项影响后果因素分别评分,再结合网络分析法计算所得的因素权重进行最终评分计算。各项因素评分由内蒙古电力公司相关专家进行综合评定后给出,其结果如图9所示。
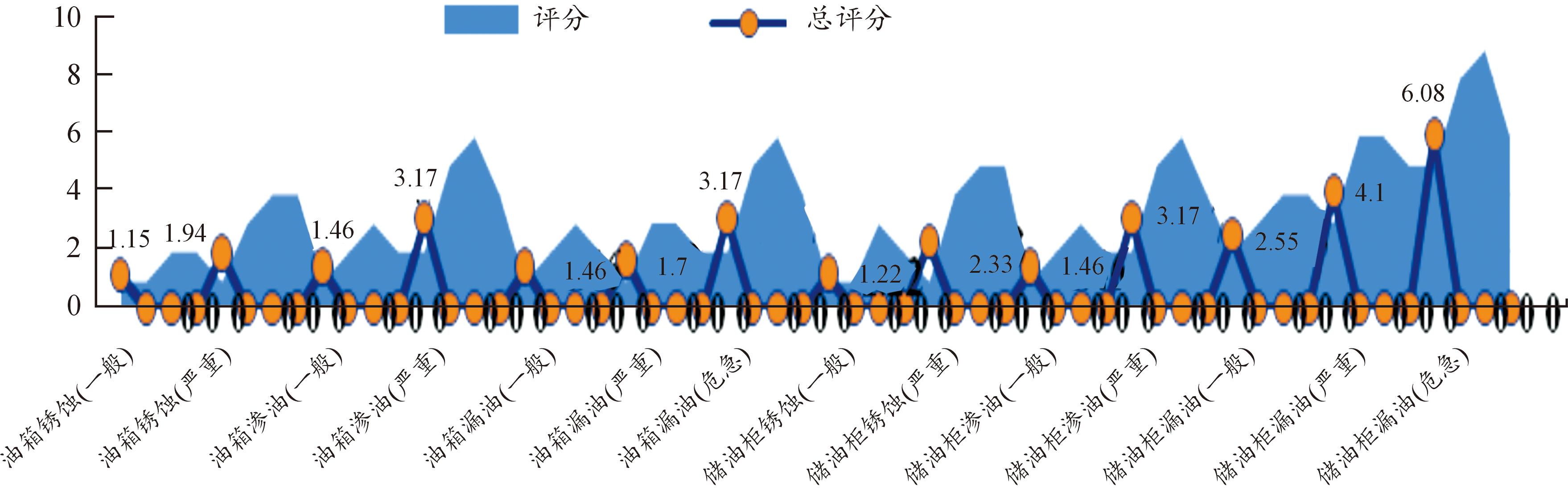
图9 ESR评分结果图
Fig.9 ESR score result chart
对油箱和储油柜渗油、漏油失效模式的影响严酷度等级进行评定,结果显示储油柜危急漏油的等级最高,为6.08,影响最严重。说明该失效一旦发生,可能会导致人员中等程度伤害、设备中等程度损坏、任务延误或降级及中等程度环境损害。储油柜严重漏油影响严酷度等级次之,为4.10。该失效一旦发生,造成的影响弱于严重漏油,强于其他渗油、漏油失效模式。
2.1.4 考虑运维成本等级的风险优先数计算及分析
基于以上评分结果,根据式 (13)计算,可得出各失效模式对应的风险优先数,其结果如图10所示。
图10 OPR,ESR,DDR和OMCR评分结果图
Fig.10 OPR,ESR,DDR,and OMCR score result chart
对于本案例中的失效模式,危急程度的储油柜漏油风险优先数为766.08,风险最高,影响最严重,是最关键的失效模式,在运行维护资源分配过程中应给予优先考虑,倾斜资源。危急程度的油箱漏油风险优先数为310.66,次之,在运行维护工作中也需要优先关注。其余失效模式,风险优先数均低于100,相较于危急程度的储油柜漏油和油箱漏油来说,风险大幅降低,在运行维护工作中可考虑维持原有资源安排或适量减少资源配置,降低成本。
与未考虑运维成本等级的风险优先数计算结果作对比,其结果如图 11所示。由图11可知,在大部分失效模式风险评分的计算中,二者的区别较小,表明在运维成本等级相似的情况下改进后的风险优先数RPN*与传统风险优先数RPN计算结果相近;少部分失效模式出现明显差异,尤其是危急程度的储油柜漏油和油箱漏油这2种情况,表明考虑运维成本等级后,某些原本风险评估较低的失效模式可能会被重新评估为高风险项。该对比说明改进后的RPN*方法更接近实际风险分析情况,不仅可以像传统RPN方法一样对电力变压器的失效模式风险进行精确量化,而且还能从运维成本的角度进行风险评价,从而更全面地反映实际电力变压器维护中的风险状况。
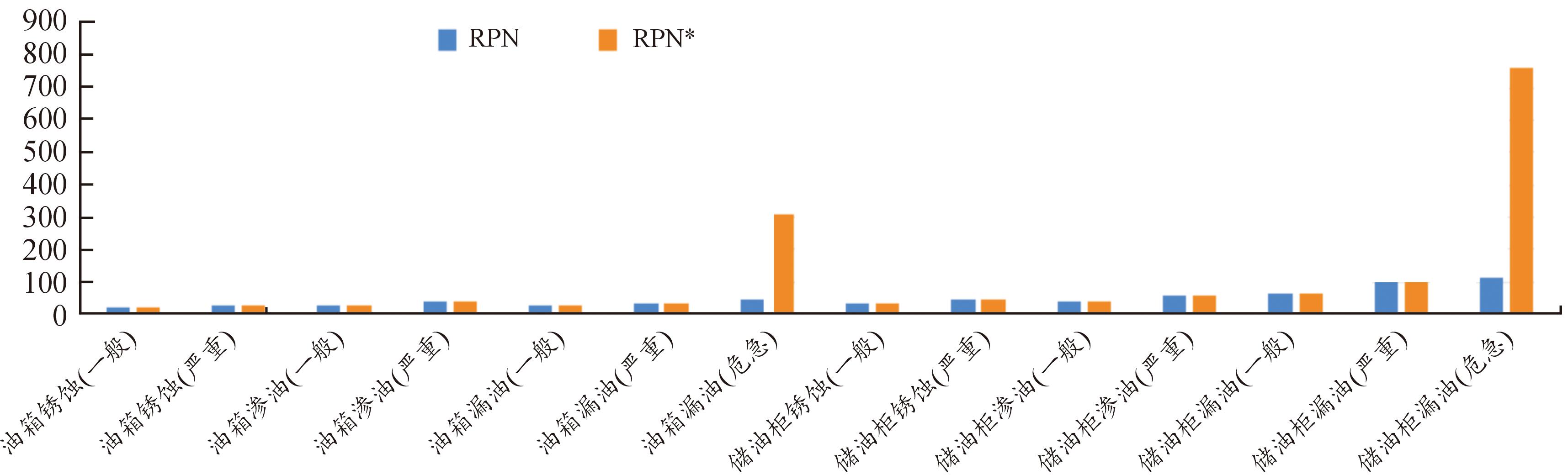
图11 改进前后的RPN对比
Fig.11 Comparison of RPN before and after improvement
图12 专家资质权重Spearman相关性热图
Fig.12 Expert qualification weight Spearman correlation heatmap
2.2 指标分析
为进一步研究关键参数变化对评估结果的影响程度,本节对方法中的关键指标与参数进行量化分析,分析过程如下:
2.2.1 专家评分相关性分析
为验证专家评分的一致性和有效性,基于表5的专家权重数据,对7位专家的评分进行了Spearman相关性分析。分析结果如图 12所示,少部分专家的平均相关系数较低,例如E1和E3、E1和E5的相关系数均低于0.6,表明少数专家存在一定的差异性;大部分专家的平均相关系数在0.68～0.83之间,相关系数较高,表明总体上专家评分具有较好的一致性,说明专家评分在总体上具备一定的一致性和有效性,能够为电力变压器的失效模式危害性分析提供有效指导。
2.2.2 参数敏感性分析
ANP的判断矩阵反映了不同风险因素间的相对重要性。本研究通过改变判断矩阵中关键元素的取值,分析其对ESR的影响。如图13所示,具体分析了人员伤害与其他3个因素(设备损坏、任务失败、环境损害)的相对重要性权重变化±30%时的情况。
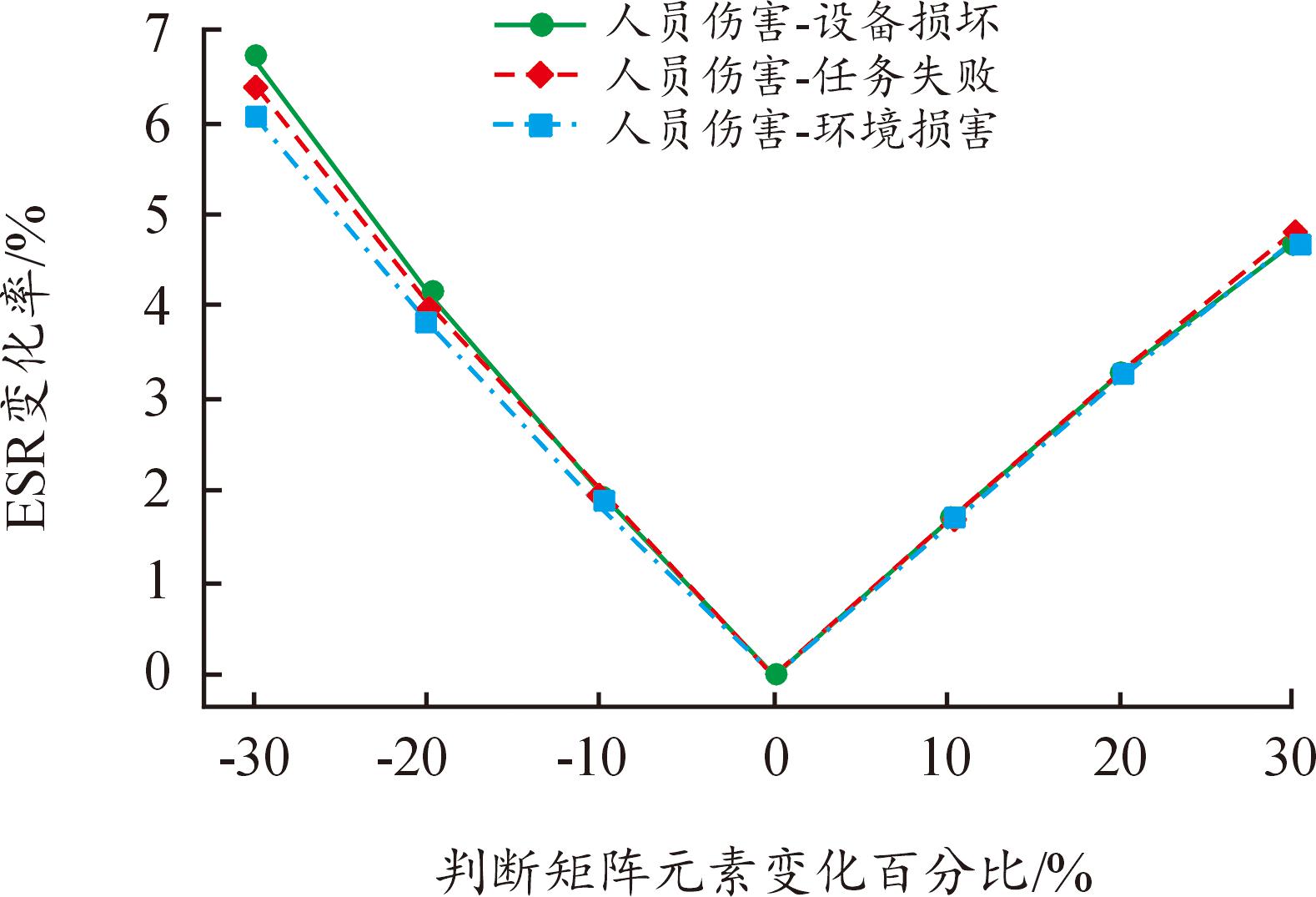
图13 ANP判断矩阵敏感性分析
Fig.13 Sensitivity analysis of ANP judgment matrix
从图像可以看出,3组因素对的敏感性曲线呈现近似的变化趋势,且呈现出对称的非线性变化特征。当判断矩阵元素变化在±10%范围内时,ESR的变化相对平缓;而当变化超过±20%时,ESR的变化率明显增大。3组因素对的敏感度差异相对较小(最大差异约0.15),说明判断矩阵具有较好的稳定性。而其中人员伤害与环境损害的权重关系对ESR的影响最大,表明本方法在严酷度等级中上人员伤害与环境损害关系是较为重要的因素。
3 结论
1) 模糊集理论量化先验经验语言:采用模糊集理论将确定的缺陷记录与不确定的模糊经验语言相结合,有效量化了评估过程中存在的不确定性和模糊性,实现了对变压器不同失效模式下失效概率的综合评估。
2) 引入网络分析法进行严酷度耦合关联分析:使用网络分析法综合考虑各影响因素之间的复杂关联关系,细化了严酷度等级评定,提高了风险评估的准确性。
3) 扩充风险分析维度:在风险分析中独立考虑运行和维护成本,采用改进的风险优先数方法,提高了成本关注度,全面衡量失效模式的风险水平,从而提升了风险评估的精确性与科学性。
实际案例应用表明,该方法在220 kV油浸式变压器的失效危害性分析中表现出显著效果。通过整合变压器的运行数据、检修记录以及专家经验判断,不仅实现了对变压器各失效模式关键程度的准确判定,还细化了风险分析内容,为实际维修策略的调整提供了更为可靠的半定量参考。虽然案例中以220 kV油浸式变压器为例,但该方法的核心思想和框架可推广至其他类型的大型电力设备,具有较好的应用前景。
然而,本方法仍存在一些局限性和改进空间。例如风险优先数的大小对具体维修策略参数(如维修间隔长短、备品备件冗余数量等)之间关系的量化指导仍显不足、未涉及长期经济因素等。未来将建立风险优先数与维修策略参数的定量映射关系,例如研究不同RPN取值区间对应的最优维修间隔、探索RPN与备品备件储备量之间的定量关系以及建立基于RPN的维修资源优化配置模型等。对这部分改进空间作进一步研究,拓宽方法的效果和适用范围。
[1] WONG S Y,YE X,GUO F,et al.Computational intelligence for preventive maintenance of power transformers[J].Applied Soft Computing,2022,114(1):108-129.
[2] 新华社.美国纽约曼哈顿突发大面积停电[EB/OL].北京:新华社,7-14[2024-11-25].http://www.xinhuanet.com/world/201907/14/c_1124751016.htm.Xinhua News.Agency a large-scale power outage occurred in Manhattan,New York,USA[EB/OL].Beijing:Xinhua News Agency.7-14[2024-11-25].http://www.xinhuanet.com/world/201907/14/c_1124751016.htm.
[3] 澎湃新闻.1死5伤!变压器突发爆炸起火[EB/OL].上海:澎湃新闻,7-27[2024-11-25].https://www.thepaper.cn/newsDetail_forward_28218050.Pengpai News.1 death and 5 injuries! transformer explosion and fire[EB/OL].Shanghai:Pengpai News,7-27[2024 -11-25].https://www.thepaper.cn/newsDetail_forward_28218050.
[4] 李宗礼.油浸式电力变压器的故障诊断方法研究[D].天津:河北工业大学,2015.LI Zongli.Study on fault diagnosis methods for the oil-immersed power transformers[D].Tianjin:Hebei University of Technology,2015.
[5] 曾芬钰,郝世旺.电力变压器设备风险评估研究综述[J].电工电气,2023(2):9-14,66.ZENG Fenyu,HAO Shiwang.Research review on the risk assessment of power transformer equipments[J].Electrotechnics Electric(Jiangsu Electrical Apparatus),2023(2):9-14,66.
[6] 严冬,王训龙.运用事故树分析电力系统越级跳闸事故[J].广东电力,2009,22(5):82-84.YAN Dong,WANG Xunlong.Using accident tree to analyze leapfrog trip accident of power system[J].Guangdong Electric Power,2009,22(5):82-84.
[7] 熊双菊,段雨舟,李孟凡,等.基于模糊故障树的配电网综合风险评估[J].广东电力,2020,33(2):93-100.XIONG Shuangju,DUAN Yuzhou,LI Mengfan,et al.Comprehensive risk assessment of distributionnetwork based on fuzzy fault tree[J].Guangdong Electric Power,2020,33(2):93-100.
[8] 李杜,雷军,万鹏.基于量化风险评估方法的电力变压器状态检修决策研究[J].科技与创新,2022(24):159-162.LI Du,LEI Jun,WAN Peng.Research on decision making for state maintenance of power transformers based on quantitative risk assessment method[J].Science and Technology &Innovation,2022(24):159-162.
[9] GUO H,WANG Y,BO H,et al.Research on reliability analysis and operation and maintenance strategy of transformers based on failure mode[J/OL].Social Science Research Network,8-26[2024-11-25].https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4917139.
[10] EYUBOGLU O H,DINDAR B,GUL O.Risk assessment by using failure modes and effects analysis (FMEA) based on power transformer aging for maintenance and replacement decision[C].IEEE,2020.
[11] MINGLIN J,REN H.Risk priority evaluation for power transformer parts based on intuitionistic fuzzy preference selection index method[J].Mathematical Problems in Engineering,2022,2022:1-10.
[12] YU H,XIONG W,XU K,et al.A risk assessment method of power transformer based on three-parameter interval grey number decision-making[J].Applied Sciences,2022,12(7):3480.
[13] PARK S H,JANG K W,KWEON D J,et al.Analysis of economic replacement cycle of power transformer based on lcc considering maintenance effect[J].Journal of Electrical Engineering and Technology,2018,13(4):1631-1637.
[14] 张博,吴杰康,罗伟明.基于模糊理论和证据理论的变压器绝缘老化状态评估[J].广东电力,2019,32(8):109-118.ZHANG Bo,WU Jiekang,LUO Weiming.Transformer insulation aging state assessment based onfuzzy theory and evidence theory[J].Guangdong Electric Power,2019,32(8):109-118.
[15] 邹国惠,魏嘉隆,王超,等.基于知识图谱的变电设备画像技术[J].广东电力,2024,37(1):86-93.ZOU Guohui,WEl Jialong,WANG Chao,et al.Knowledge graph-based portrait depiction technology for substation equipment[J].Guangdong Electric Power,2024,37(1):86-93.
[16] 苏宇飞,杜鸿云,温新鹏.电力变压器常见故障处理及预防研究[J].光源与照明,2024(2):168-170.SU Yufei,DU Hongyun,WEN Xinpeng.Power transformer common fault processing and prevention research[J].Lamps &Lighting,2024(2):168-170.
[17] GUO X,JI J,KHAN F,et al.Fuzzy bayesian network based on improved similarity aggregation method for risk assessment of storage tank accident[J].Process Safety and Environmental Protection,2021,149:817-830.
[18] HSU H M,CHEN C T.Aggregation of fuzzy opinions under group decision making[J].Fuzzy Sets and Systems,1996,79(3):279-285.
[19] 李波,张文乾,刘维,等.基于熵权层次法的油浸式变压器绝缘状态评价[J].电力工程技术,2023,42(4):223-230.LI Bo,ZHANG Wenqian,LIU Wei,et al.Insulation condition evaluation of oil-immersed transformer based on entropy weight hierarchy method[J].Electric Power Engineering Technology,2023,42(4):223-230.
[20] SAATY T L.Decision making with dependence and feedback[M].RWS Publication,Pittsburgh,PA,1996:28-30.
[21] 兰芳.基于FISM-ANP-灰色聚类的软件项目开发风险评价研究[D].成都:电子科技大学,2018.LAN Fang.Risk evaluation of software proiect development based on FISM-ANP-grey clustering[D].Chengdu:University of Electronic Science and technology,2018.
[22] ISO.Risk management—principles and guidelines[S].Geneva:ISO,2009.
[23] 邵强,林向义.基于ANP的国际石油工程项目风险评价研究[J].科技进步与对策,2010,27(11):127-130.SHAO Qiang,XIN Xiangyi.Risks evaluation on international petroleum engineering project based on ANP[J].Science &Technology Progress and Policy,2010,27(11):127-130.
[24] ASWIN K R,RENJITH V R,AKSHAY K R.FMECA Using fuzzy logic and grey theory:Acomparitve case study applied to ammonia storage facility[J].International Journal of System Assurance Engineering and Management,2022,13(4):2084-2103.
[25] 卢艺,卢苑,何晓峰,等.电网风险量化评估方法与管控实践[J].广东电力,2018,31(5):49-55.LU Yi,LU Yuan,HE Xiaofeng,et al.Risk quantification assessment method and management control practice of power grid[J].Guangdong Electric Power,2018,31(5):49-55.