0 引言
以可再生能源制取氢能,是实现交通和分布式能源领域低碳化的重要路径,对于我国实现“2030碳达峰、2060碳中和”具有重要意义[1-3]。氢能产业链包括制氢、储运和利用3个主要环节[4-5]。交通领域的氢气利用主要是氢燃料电池汽车,车辆的燃料加注主要发生在加氢站,因此加氢站是连接产业链上游制氢和下游应用的重要枢纽[6-8]。根据中国氢能联盟统计,截至2021年12月,全球已建成687座加氢站,以70 MPa高压气态加氢站为主,占比70%以上[9]。2020年,中国发布了《节能与新能源汽车技术路线图2 0》,指出2025年将建成加氢站1 000座,2030年将建成5 000座[10]。
现今,加氢站的氢源一般来自城市周边的制氢厂,大规模氢源供应方式为管道输送,对于城市中分散式加氢站,目前主要采用管束车供氢[11]。因此,针对典型的城市周边集中式制氢-市内多个加氢站分散式供氢场景,一般采用加氢站选址规划和管束车供氢调度2种方案减少输运成本。目前,研究人员已采用人工智能、模型搭建-算法模拟等方法对加氢站选址规划开展了大量研究[12]。采用管束车输配氢气时,管束车所运氢气的质量只占总运输质量的1%~2%,并且氢气瓶卸气时间较长,导致运输效率较低[13]。因此,应对管束车供氢进行合理的调度,以提高管束车利用率,减少综合运氢里程,从而降低氢气输配成本[14]。然而,当前缺乏全局规划的管束车供氢调度机制,多数以加氢站的短期需求为依据进行临时性管束车氢气调配,这导致运氢成本普遍偏高。加氢站用氢的运输方式要考虑满足调度周期内每个加氢站的全部用氢需求,同时兼顾经济性。
本文分析了加氢站氢气供应问题的影响因素,综合考虑了制氢站充装能力、管束车运输能力和加氢站加注能力以及加氢站物理位置,建立了加氢站氢气供应车辆调度的数学模型,进一步分析了与常见路径规划问题的区别,以满足加氢站最小储氢量和加注需求且运输成本最小化为目标,采用大规模邻域搜索算法优化标准的遗传算法求解问题,获得成本较低的加氢站氢气供应调度方案,并通过试验证明方法的有效性和可行性。进一步验证了站内备用管束对氢气运输成本的影响。
1 加氢站氢气供应问题
多辆管束车在制氢站充满氢气后分别向配送范围内的多个固定位置的加氢站供应氢气。管束车每次卸气结束后返回制氢站充气,每次充气量为管束的最大装载量,充满气后为1个或多个加氢站供应氢气。根据每个加氢站的日加注能力和站内储氢量计算出1次或多次氢气供应需求量和配送时间。
假设在一个配送周期T内,N个加氢站共提出了H项氢气供应需求,需要M辆管束车输配,采用表达式为
![]()
(1)
![]()
(2)
式(1)、式(2)中:qi_s表示每个加氢站每次供应的氢气量;n表示加氢站的氢气需求次数,根据日加注能力和站内储氢量计算,每个站不同;qr表示每个需求项的氢气量;V表示管束车平均行驶速度;T表示一个调度周期;tk_unload表示管束车在加氢站的服务时长,即每次服务的等待时长与卸气时长之和;tk_fill表示管束车总充气时长,即充气次数与单次时长的积;tk_idle表示管束车空闲时长;d表示管束车经过满载-空载-满载一个完整状态所行驶的距离。
加氢站的氢气供应需求信息根据每个站的日加注负荷和站内储氢能力,预测一个调度周期的供应需求量和配送时间。氢气需求量以初始站内储氢量为基准,以站内最大储氢量为边界,根据日加注负荷曲线计算氢气消耗量,在管束车开始卸气时更新站内储氢量。因此,将站内储氢容量可以容纳一定气量的时刻作为最早配送时间,达到储气量下限的时刻作为最晚配送时间。氢气需求量由站内储氢能力和剩余气量确定,上限为管束车的最大载气量。依次制定N个加氢站在调度周期内的全部加氢需求,获得H项氢气需求列表。
假设制氢站气源充足,每辆管束车到站后无须等待立即充气,充满后离开。充气时长表达式为
![]()
(3)
式(3)中:Q表示管束车最大载气量;Cfill表示制氢站压缩机排量。
管束车在加氢站内的卸气时长与加氢站类型和站内储氢量有关。若为固定站,站内无备用长管时,卸气时长为需求量与压缩机排量Crefuel的比值,站内有备用长管时,卸气时长等价为更换长管的时间treplace。若为撬装站,根据站内剩余气量qsurplus和压缩机排量Crefuel计算管束车等待时间,根据历史加注数据估算卸气时长,两者之和为实际卸气所需时间。卸气时长tunload表达式为
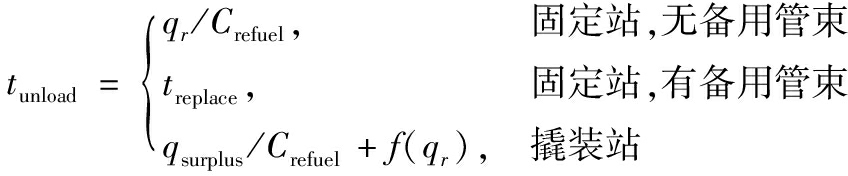
(4)
分析可知,影响加氢站氢气供应的主要因素如图1所示。在制氢站充装能力和加氢站加注能力已确定的应用场景下,选择配置备用长管或储氢量少、加注负荷低的工况卸气等方式可以缩短卸气时长;加氢站氢气需求信息的准确性是车辆合理安排服务的基础,可以有效缩短空闲时长。因此,如何在满足加氢站用氢需求的前提下尽可能地减小管束车空闲时间、缩短行驶距离,采用合理的氢气配送方案对减少加氢站氢气供应所需管束车数量至关重要。
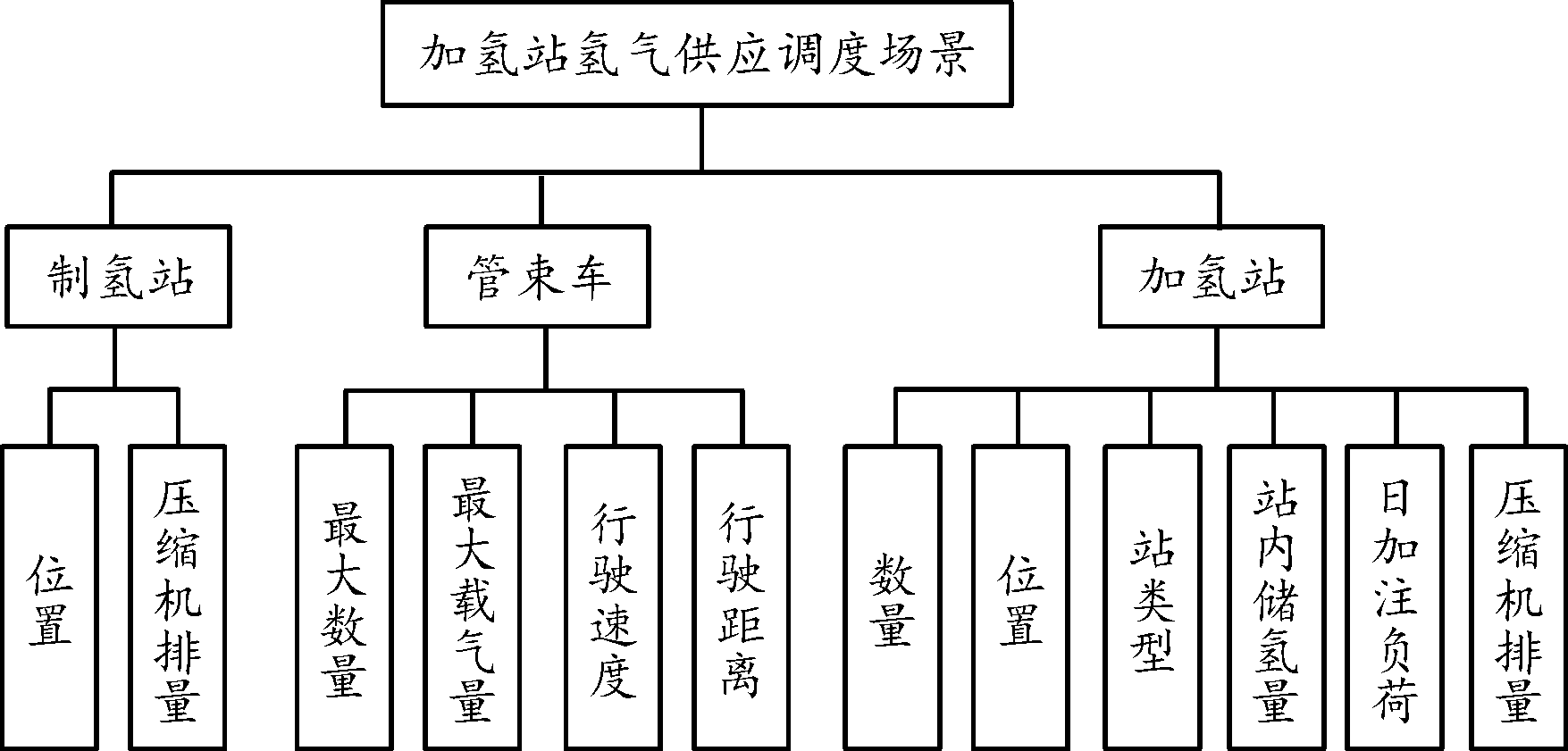
图1 加氢站氢气供应调度影响因素
Fig.1 Factors affecting hydrogen supply and dispatch at hydrogen refueling station
2 氢气供应车辆调度模型
2.1 优化模型
加氢站氢气供应车辆调度问题模型为:站点用i(i=-1,0,1,…,n)表示,-1表示制氢站,0表示停车点,1,2,…,n表示加氢站;停车点的管束车用k(k=1,2,…,m)表示,氢气需求列表用集合S(S={Sr|r=1,2,…,h})表示,每个需求项Sr服务于一个加氢站,每个加氢站可以有1个或多个需求项;每个需求项的一次需求量为qr,在配送时间窗[er,lr]内到达,经过服务时长wr后离开加氢站。管束车离开后,根据载气量选择驶向制氢站充气,或回到停车点,或驶向下一个需求对应的加氢站。
决策变量定义为

(5)

(6)
![]()
(7)

(8)
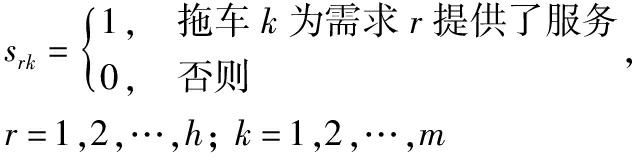
(9)
根据式(5)—式(9)的符号定义,建立加氢站氢气供应的运输成本模型为
![]()
(10)
式(10)中: Cr为车头的固定投资成本;Ct为管束的固定投资成本;Cp为车的单位运维成本;dij为距离矩阵,表示站点i与站点j之间的行驶距离,dij=dji;pi为加氢站i的卸气车位个数。
式(10)为目标函数,表示最小化供氢成本。管束车的成本包括车头和管束2个部分费用。
约束条件定义为
![]()
(11)
![]()
(12)
qrsrk≤Q, r=1,2,…,h; k=1,2,…,m
(13)
uriqr≤piQ, r=1,2,…,h
(14)
er≤fkr≤lr, r=1,2,…,h; k=1,2,…,m
(15)
r=1,2,…,h; s=1,2,…,h
(16)
式(11)—式(16)中:Q为管束最大氢气装载量;V为管束车平均行驶速度; fkr为车k到达第r个需求对应的加氢站的时间;M为罚因子。
式(11)表示加氢站提出的每个需求都能得到服务,且仅被服务一次。式(12)表示如果车k到达了需求r对应的站,则必须为需求r提供服务。式(13)表示一辆管束车服务所有需求的总需求量不会超过其最大装载量。式(14)表示每个需求的实际需求量不能大于站内可同时卸气的总容量。式(15)表示每辆车在服务每个需求时,到达站的时间在时间窗内。式(16)表示当管束车服务多个需求时,相继到达2个站之间的时间关系。
2.2 模型分析
分析氢气供应车辆调度数学模型,发现与有时间窗车辆路径问题(vehicle routing problems with time windows,VRPTW)[15-16]有一些相似之处,如为一定数量的加氢站提供配送服务,有不同需求时间和气量的配送需求,运输载体是多辆管束车,目标是在需求时间窗内配送指定量的氢气,并行驶路程最短、所需车辆最少。但加氢站用氢气供应调度问题有其特别之处,主要表现在:
1) 一个调度周期内每个加氢站可以有一次需求,也可以有多次需求,与常规VRPTW中一个目的地对应一次服务不同;
2) 每个加氢站可以同时有一辆或多辆管束车(不超过站内卸气车位)进行卸气,与常规VRPTW中一个目的地同时只有一个车辆进行服务有所不同;
3) 加氢站内压缩机的排气能力主要取决于站的设计加注能力,配置不相同,并且有些站有备用管束用于替换管束车的管束,根据设备配置计算得到的管束车在每个站内的服务时间不同;
4) 每个站的储氢量和加注负荷不同,因此每个站在调度周期内的氢气需求量不同,因此管束车配送的时间和次数需要定制化处理,才能既满足站内储氢要求,又能减少车辆等待时间。
这些应用场景与传统VRPTW应用场景有着明显不同,因此传统VRPTW常用的解决方法不能直接应用,需要根据加氢站氢气供应调度优化问题的特点针对性地做出改进。
2.3 模型求解
遗传算法(genetic algorithm,GA)能够模拟大自然中生物进化的原理并从中获取灵感,它是以自然界基因筛选机制为基本思想,形成一套模拟的进化算法来求解现实中的复杂问题[17-20]。该算法能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最优解。其优越性主要表现在算法具有很强的搜索能力,能以较高的概率找到问题的全局最优解;其次,由于它固有的并行性,能有效处理大规模的优化问题。因此本文选择遗传算法对构建的氢气供应调度模型进行求解,对算法的实现方式进行优化处理。
针对氢气供应车辆调度数学模型,本文采用整数作为染色体的编码,对于实际需要解决配送问题的氢气需求项采用1,2,…,正整数表示,对于辅助配送的制氢站用-1表示,管束车统一停放站点用0表示。后续可根据供应网中制氢站数量增加,采用负整数表示,扩展管束车的充装氢气范围。这种编码方式可以方便地得到为每个加氢站服务的管束车编号,也可以获知每辆管束车的充气、卸气状态以及位置信息。所设计的染色体具有每个路径之间无序,路径内部有序的特点。
根据全部加氢站的需求项个数随机产生整数序列,初始化种群。根据车载氢气量、需求量和配送时间约束,查看当前生成的整数序列中未进行服务的配送需求项,如果满足要求则查看下一个,否则在其后插入表示制氢站的-1,继续判断充装氢气后是否满足下一个站的配送要求,如不满足,则在其后插入表示调度站的0,表示管束车充装结束后回到调度站等待下一次配送,如满足,则继续判断下一个需求。如此反复,直至对全部需求项进行服务。由此生成一组具有多个配送路径的配送方案,作为初始种群的一个个体,进而依次重复该过程产生足够的种群个体。
适应度函数如式(17)所示,由3项组成:第1项为实际车头、管束、人工和行驶距离产生的成本之和,以每公斤氢气的成本表示;第2项αq中q表示各条路径违反的容量约束之和,α为违反容量约束的惩罚函数系数;第3项βw中w表示所有需求违反的时间窗约束之和,β为违反时间窗约束的惩罚函数系数。
fit=(Ctriler+Ctube+Clabor+Cdist)/MH2+αq+βw
(17)
选择操作采用二元锦标赛选择法,交叉操作采用顺序交叉,变异操作采用交换变异。
为了提高求解质量,对变异后产生的群体采用大规模邻域搜索算法(large neighborhood search,LNS)。由于常规的LNS通过使用试探法来探索复杂的邻域,因此搜索过程比较耗时。本文针对加氢站氢气配送调度问题,采用对前k个最小目标值、前k个最大目标值,以及随机选择k个不重复的解进行移出和重新插入处理,在提高求解质量的基础上缩短求解时间。首先使用移除算子,根据距离的相关性,移除相关性较低的若干个需求。距离相关性的计算方式为
![]()
(18)
![]()
(19)
式(18)、式(19)中:Rmn表示一个路径中移除的需求项与剩余的每个需求的距离相关性;DSMmax为停车点到其他所有站的距离的最大值,当该项需求为管束车的最大装载量时;d为加氢站之间的距离和管束车在制氢站充气的行驶距离,否则为2个加氢站的距离;dmA、dAB、dBn依次表示加氢站m至制氢站、制氢站至停车点、停车点至加氢站n的距离;dmn表示加氢站m和n的距离。
然后使用插入算子将被移除的需求重新插回到解中,插入位置点根据插入被移除需求后,不仅满足时间窗和容量的约束,而且距离增量最小的指标进行评价和选择。
3 结果讨论
3.1 方法验证
以1个制氢站和10个加氢站为例,验证提出的加氢站氢气供应调度模型的有效性。假设管束车最大氢气装载量400 kg,平均行驶速度50 km/h,车头价格60万元/台,管束价格80万元/组,管束满载时的氢气量为320 kg,人工费 15万元/年/人,平均维修费100元/100 km,燃料经济性为 40 L/100 km,油价7元/L,管束利用率为0.8,人员配比1.2。加氢站2#和8#分别有1个备用长管。调度周期24 h,在早晨 5∶00开始配送。停车点、制氢站与加氢站之间的距离矩阵如图2所示,其中,-1表示制氢站,0表示停车点,其他整数表示加氢站,管束车的运输范围在200 km内。模型及算法开发软件为MATLAB R2019。
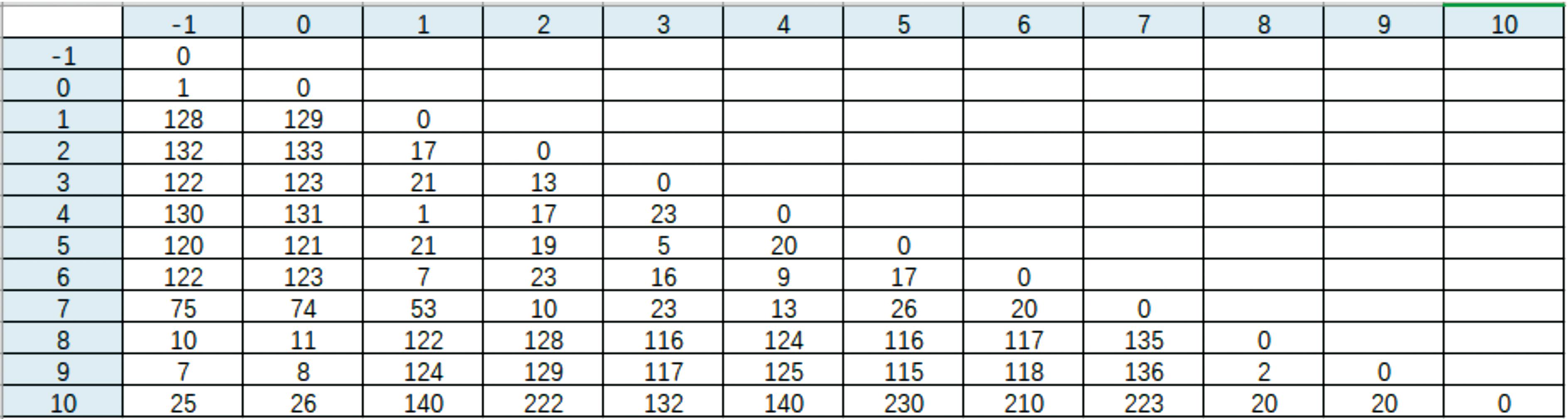
图2 氢气供应链站点距离矩阵
Fig.2 Schematic of the hydrogen supply chain site distance matrix
每个加氢站的初始站内储氢量如表1所示。
表1 调度初始时加氢站站内储氢量
Table 1 Amount of hydrogen stored in the hydrogen refueling station at the beginning of the dispatch
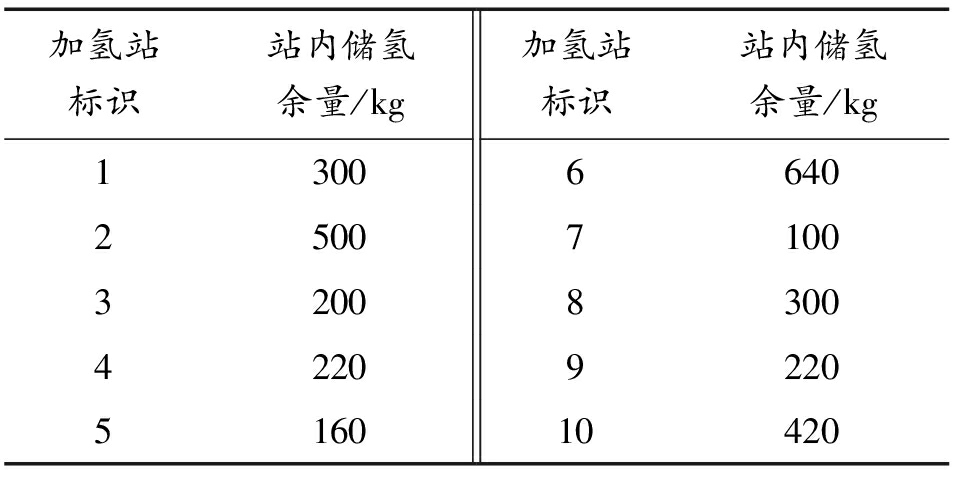
加氢站标识站内储氢余量/kg加氢站标识站内储氢余量/kg13006640250071003200830042209220516010420
考虑到上一次调度周期结束时,有部分管束车可能仍在一些加氢站内卸气。因此在每次调度开始时,需要根据每辆管束车的初始位置修正氢气配送需求表。管束车的初始位置信息如表2所示,其余管束车在停车点。
表2 管束车初始位置
Table 2 Initial position of the tube bundle car

目的地(站标识)与目的地的距离/km车载气量/kg130300250200360150
根据加氢站的日加注负荷曲线、加注能力、压缩机排量和备用管束数量等参数信息,按照以加氢站内能储存下一次运输的氢气量的时刻作为最早服务时间,以站内储氢量剩余20%气量的时刻作为配送的最晚时间规则,计算获得调度周期内的配送次数及每次的配送时间窗口和卸气时长,该信息作为氢气配送的基本需求。另外,将加氢站已经有管束车卸气的情形作为新的需求项。两部分信息合并得到调度周期内加氢站氢气需求表,如表3所示。
表3 加氢站氢气需求
Table 3 Hydrogen demand for hydrogen refueling stations
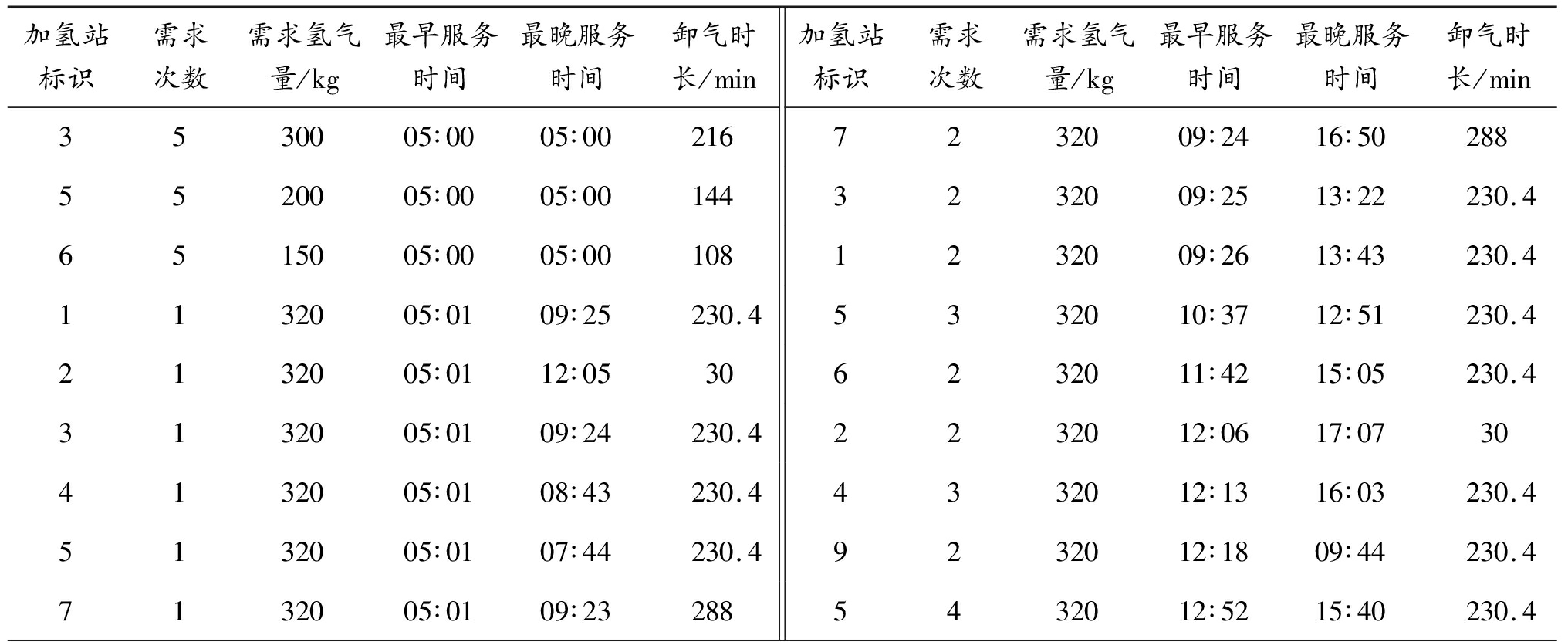
加氢站标识需求次数需求氢气量/kg最早服务时间最晚服务时间卸气时长/min加氢站标识需求次数需求氢气量/kg最早服务时间最晚服务时间卸气时长/min3530005∶0005∶002167232009∶2416∶502885520005∶0005∶001443232009∶2513∶22230.46515005∶0005∶001081232009∶2613∶43230.41132005∶0109∶25230.45332010∶3712∶51230.42132005∶0112∶05306232011∶4215∶05230.43132005∶0109∶24230.42232012∶0617∶07304132005∶0108∶43230.44332012∶1316∶03230.45132005∶0107∶44230.49232012∶1809∶44230.47132005∶0109∶232885432012∶5215∶40230.4
续表(表3)

加氢站标识需求次数需求氢气量/kg最早服务时间最晚服务时间卸气时长/min加氢站标识需求次数需求氢气量/kg最早服务时间最晚服务时间卸气时长/min6132006∶2311∶41230.43332013∶2320∶59230.48132007∶0109∶51301332013∶4419∶16230.49132007∶0112∶17230.46332015∶0618∶19230.410132007∶0116∶54230.42332017∶0807∶07305232007∶4510∶36230.46432018∶2022∶16230.44232008∶4412∶12230.43432021∶0011∶01230.4
按照需求表服务时间顺序,根据配送时间和卸气时长为每个需求项逐一安排配送车辆。得到的初始路线如图3所示,共需要19辆管束车,共行驶6 051 km,即氢气运输成本为4.5 701元/kg。初始路线图中每条路线表示每辆车配送过程中需要经停的站点及满足的需求项,例如路线4表示从停车点出发,到加氢站4#服务其第1次气源需求,卸气结束后返回制氢站充气,再驶回停车点等待,继续到加氢站3#服务其第4次需求,结束后先返回制氢站充气最后返回停车点。

图3 加氢站氢气供应初始路线
Fig.3 Schematic of the initial route of hydrogen supply at the hydrogen refueling station
基于提出的氢气供应车辆调度数学模型,模拟当前应用场景,采用遗传算法直接优化求解。遗传算法有4个运行参数需要预先设定,即种群大小、终止进化代数、交叉概率、变异概率。经过多次实验调试,最终设定种群大小取100,终止进化代数30,交叉概率0.85,变异概率0.05。以上述初始路线作为初始种群,优化过程的目标迭代如图4所示,氢气供应的甘特图如图5所示,共需要18辆管束车,调度周期内共行驶6 043 km,氢气运输成本为4.3 106元/kg,比初始方案的氢气成本降低了5.68%。

图4 GA算法目标收敛迭代过程
Fig.4 Iterative process representing target convergence by GA algorithm
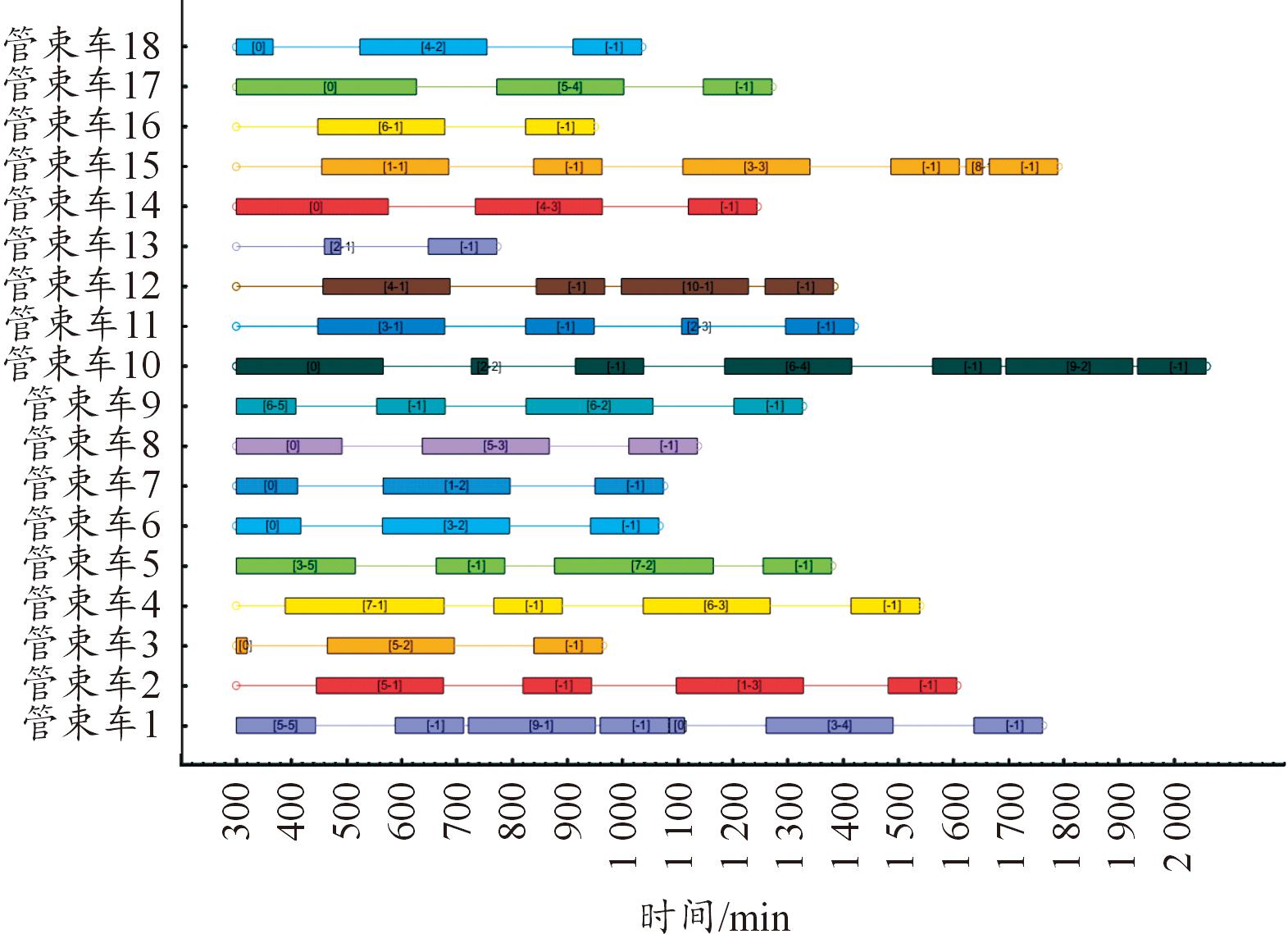
图5 GA优化后的加氢站氢气供应甘特图
Fig.5 Gantt diagram of hydrogen supply of the hydrogen refueling station optimized by the GA method
进一步地,采用GA和LNS方法求解,设置移除数量为需求项数量的1/3,目标收敛迭代过程如图6所示,氢气供应的甘特图如图7所示。本方案可满足全部氢气需求列表中的氢气总量9 290 kg,按照配送方案甘特图的时间安排进行配送,可满足全部需求的时间窗,这体现了该方法的准确性和可行性。优化后的氢气供应路线需要16辆管束车,配送周期内行驶距离为6 041 km,氢气运输成本为4.1 072 元/kg。

图6 GA算法目标收敛迭代过程
Fig.6 Iterative process representing target convergence by GA+LNS algorithm
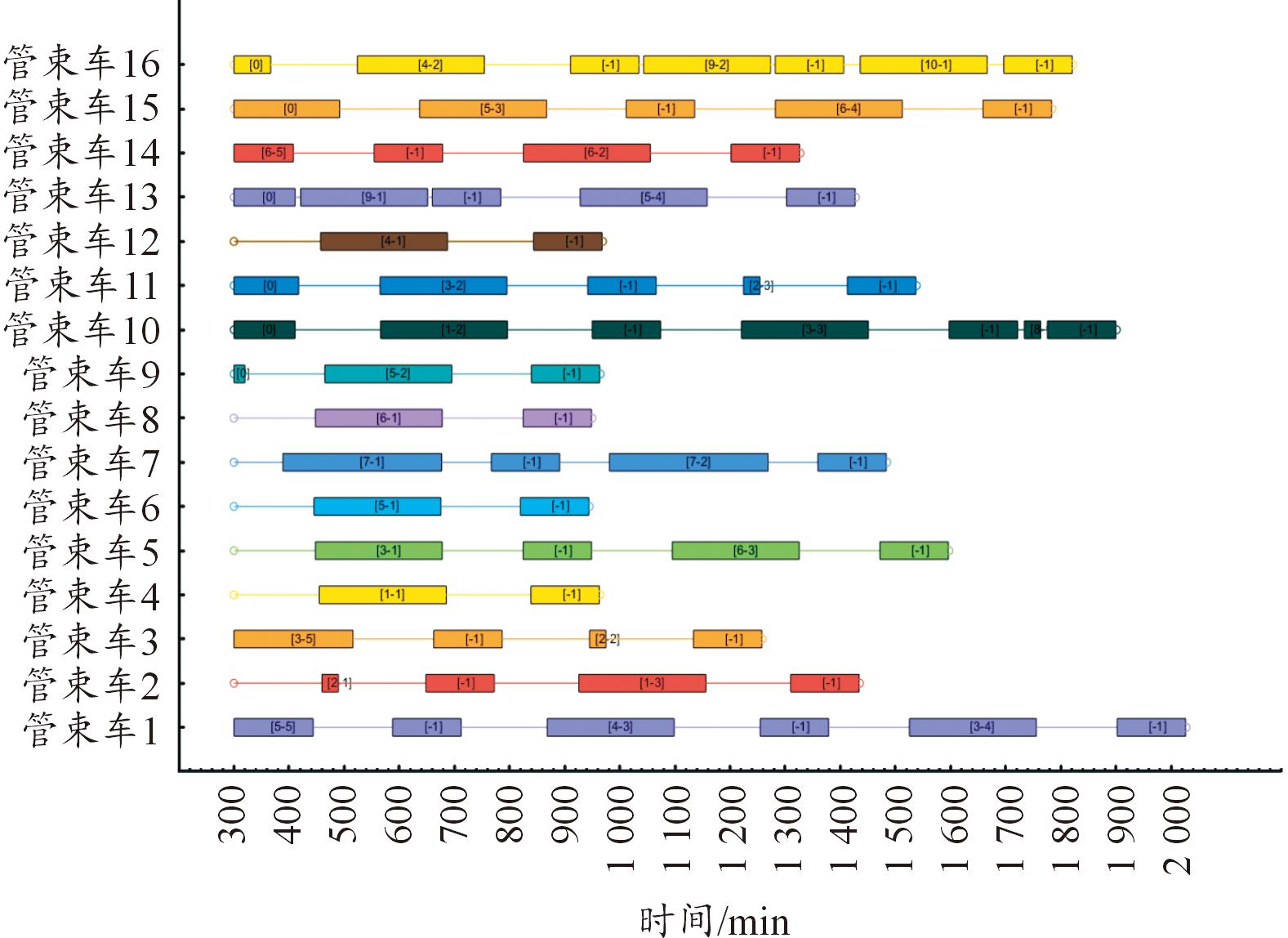
图7 采用GA+LNS方法优化后的加氢站氢气供应甘特图
Fig.7 Gantt diagram of hydrogen supply of the hydrogen refueling station optimized by the GA+LNS method
对比分析初始方案和优化方案,如图8所示。与初始方案对比,管束车减少了3辆,行驶距离减少了10 km,氢气运输成本减少了0.462 9元/kg,降低了10.12%。与仅采用GA算法的方案相比,需要的管束车少2辆,氢气运输成本减少了4.72%,表明采用LNS改进的GA方法可以有效解决加氢站氢气供应调度问题,获得经济性更高的调度方案,体现了该方法的优越性。
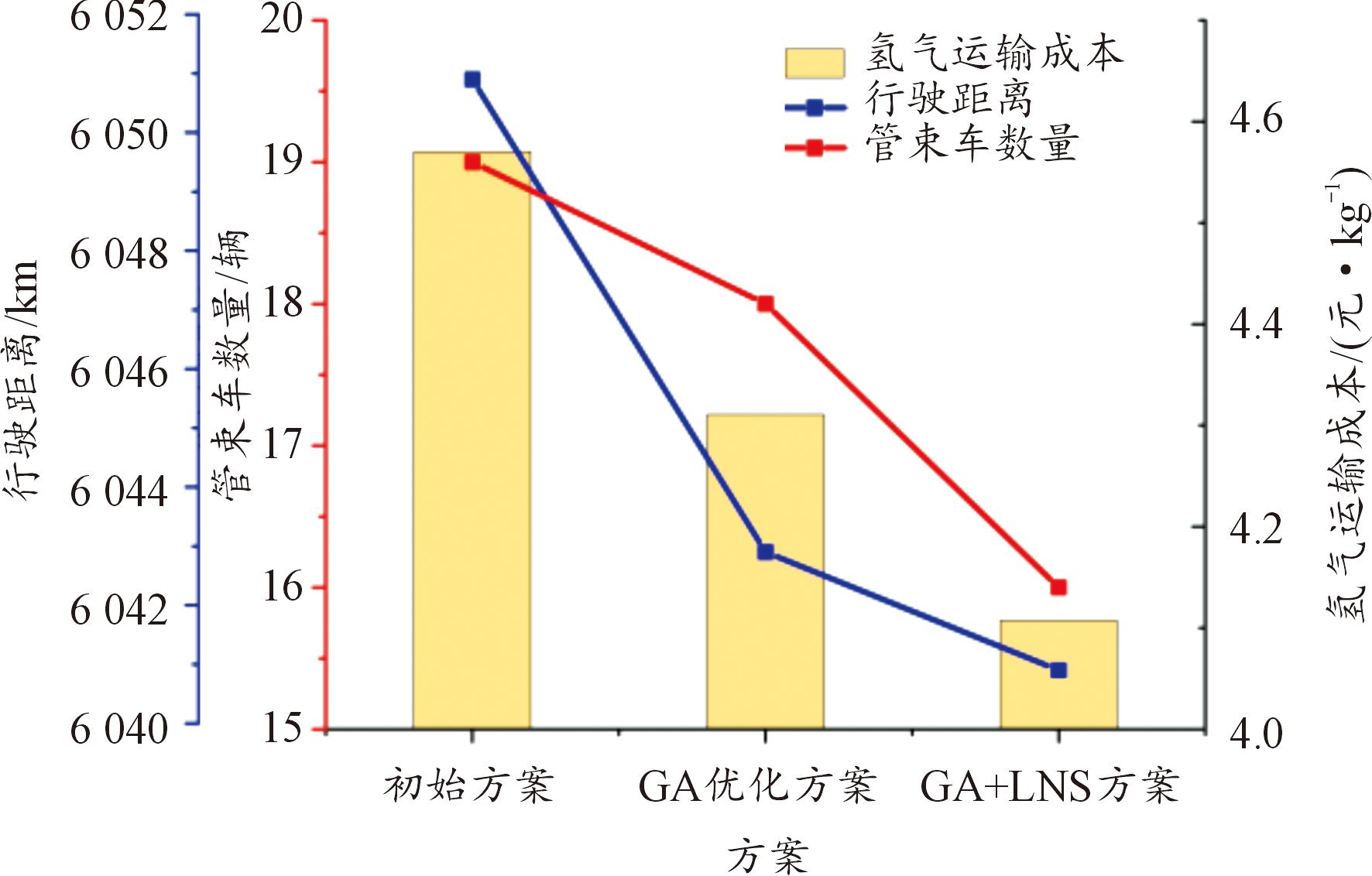
图8 3种方法的调度方案对比
Fig.8 Comparison of scheduling schemes for the three methods
3.2 加氢站卸气时间的影响分析
上述设置中有2个加氢站(2#和8#)设置了备用长管,因此2个站的卸气时间与其他加氢站相比,服务时间短,参考表 3。为了进一步分析加氢站卸气时间对管束车运输氢气成本的影响,对4个加氢站(2#、5#、8#、10#)分别有1个备用管束、全部加氢站都无备用管束等2种情形,分别计算获得新的加氢站氢气需求表,采用与前述方法相同参数设置的GA+LNS方法进行求解。
3种备用管束配置的氢气配送方案如图9所示,管束车所需数量分别是17、16、15辆,行驶距离依次是6 043、6 041、 6 039 km,由于管束车数量和行驶距离的减少,导致氢气运输成本也依次降低,分别是4.179 8、4.107 2、4.034 6元/kg。结果表明增加备用管束的配置使得管束车在加氢站内的服务时间缩短,进而减少了管束车总数量和行驶距离,使得氢气运输成本减少。由此说明增加站内管束,可以提高管束车运输能力利用率,有效降低氢气运输成本。
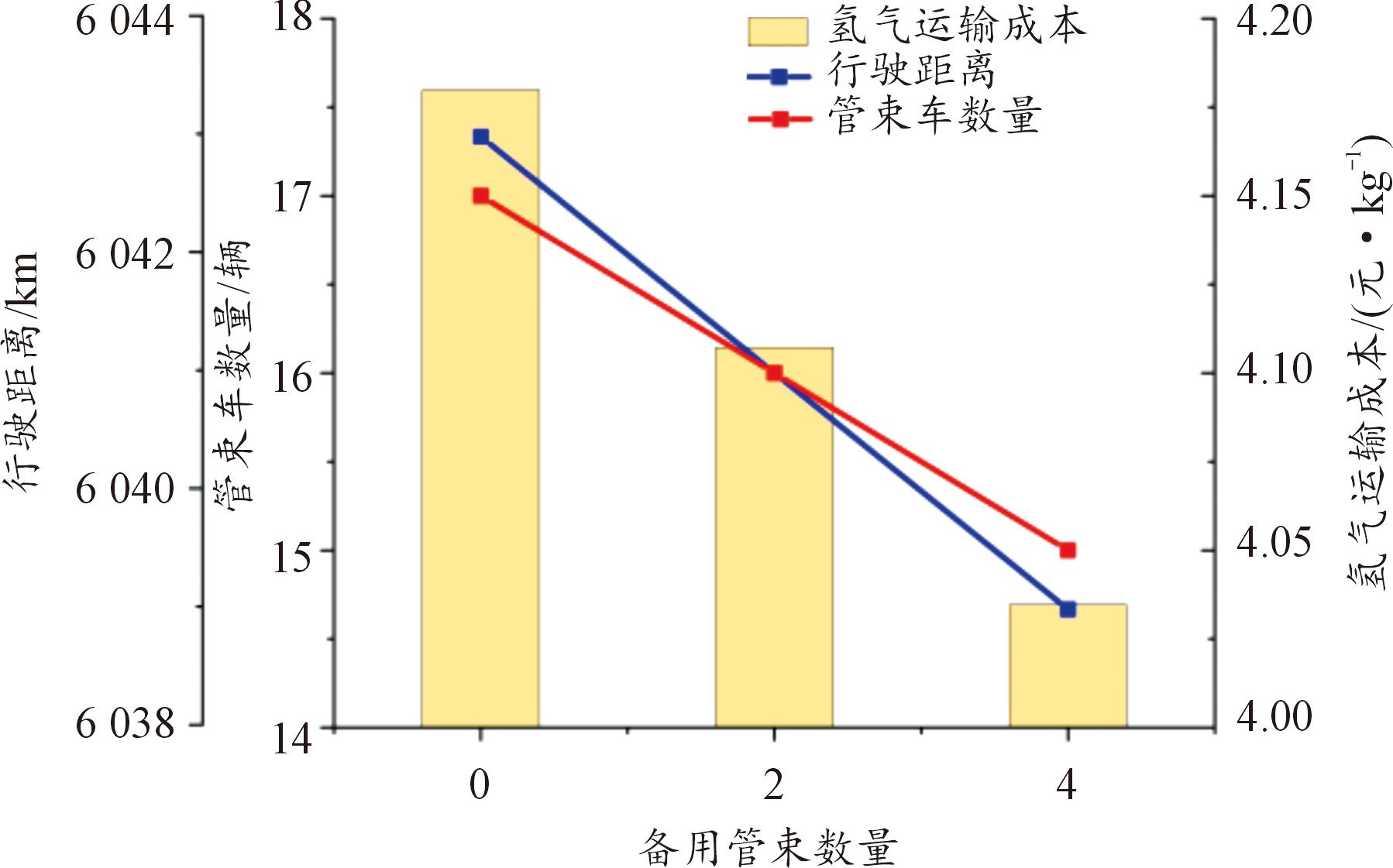
图9 3种备用管束配置的氢气调度方案对比
Fig.9 Comparison of hydrogen scheduling schemes for three standby tube bundle configurations
4 结论
本文采用大规模邻域优化的遗传算法求解,获得了低成本的加氢站用氢气调度方案。
1) 针对设定的加氢站用氢气供应场景,利用开发的算法能够减少管束车数量15%,实现氢气综合输配成本降低10%。通过减少车辆等待时间提高了车辆利用率,降低车辆需要数量和缩短行驶距离,降低了氢气运输成本。
2) 提出在加氢站氢气供应调度问题中增加加氢站站内备用管束,发现在不考虑备用管束对加氢站占地面积的额外影响下,增加备用管束可以减少管束车数量,也可以降低氢气运输成本。后续在加氢站供应网络规划时可综合考虑储罐、管束等站内储氢形式,既满足加注负荷需求,又能促进管束车利用效率。
3) 随着储氢技术发展,管束车的管束通过技术升级可大幅度提高载氢量,本文提出的调度模型和求解方法已考虑该情形并具有较好的扩展性,仍然可应用于管束车的高效调度和运输管理,致力于降低氢气在交通领域的应用成本。
[1] OLIVERIRA A M,BESWICK R R,YAN Y.A green hydrogen economy for a renewable energy society[J].Current Opinion in Chemical Engineering,2021,33:100701.
[2] JIANG J,XUN K,LIU Y,et al.Hydrogen production technology promotes the analysis and prospect of the hydrogen fuel cell vehicles development under the background of carbon peak and carbon neutrality in china[J].ACS Omega,2022,7(45):40625-40637.
[3] BROCKWAY P E,OWEN A,BRAND-CORREA L I,et al.Estimation of global final-stage energy-return-on-investment for fossil fuels with comparison to renewable energy sources[J].Nature Energy,2019,4:612-621.
[4] 单彤文,宋鹏飞,李又武,等.制氢、储运和加注全产业链氢气成本分析[J].天然气化工—C1 化学与化工.2020,45(1):85-96.SHAN Tongwen,SONG Pengfei,LI Youwu,et al.Cost analysis of hydrogen from the perspective of the whole industrial chain of production,storage,transportation and refueling[J].Low-carbon Chemistry and Chemical Engineering,2020,45(1):85-96.
[5] YANG Y,TONG L,YIN S,et al.Status and challenges of applications and industry chain technologies of hydrogen in the context of carbon neutrality[J].Journal of Cleaner Production,2022,376:134347.
[6] GENOVESE M,FRAGIACOMO P.Hydrogen refueling station:overview of the technological status and research enhancement[J].Journal of Energy Storage,2023,61:106758.
[7] LUNDBLAD T,TALIJEGARD M,JOHNSSON F.Centralized and decentralized electrolysis-based hydrogen supply systems for road transportation-a modeling study of current and future costs[J].International Journal of Hydrogen Energy,2023,48:4830-4844.
[8] LIN R,YE Z,GUO Z,et al.Hydrogen station location optimization based on multiple data sources[J].International Journal of Hydrogen Energy,2020,45(17):10270-10279.
[9] 刘玮,万燕鸣,熊亚林,等.中国氢能源及燃料电池产业发展报告2020[M].北京:人民日报出版社,2021.LIU Wei,WAN Yanming,XIONG Yalin,et al.China hydrogen energy and fuel cell industry development report 2020[M].Beijing:People′s Daily Press,2021.
[10] 中国汽车工程学会.节能与新能源汽车技术路线图2.0[M].北京:机械工业出版社,2020.Society of Automotive engineers of china.roadmap for energy saving and new energy vehicles 2.0[M].Beijing:China Machine Press,2020.
[11] PESCHEL A.Industrial perspective on hydrogen purification,compression,storage,and distribution[J].Fuel Cells,2020,20(4):385-393.
[12] CROENERT T,MINNER S.Location selection for hydrogen fuel stations under emerging provider competition[J].Transportation Research,Part C.Emerging Technologies,2021,133:103426.
[13] 张轩,樊昕晔,吴振宇,等.氢能供应链成本分析及建议[J].化工进展,2021,41(5):2364-2371.ZHANG Xuan,FAN Xinye,WU Zhenyu,et al.Hydrogen energy supply chain cost analysis and suggestions[J].Chemical Industry and Engineering Progress,2021,41(5):2364-2371.
[14] ELGOWAINY A,REDDI K,SUTHERLAND E,et al.Tube-trailer consolidation strategy for reducing hydrogen refueling station costs[J].International Journal of Hydrogen Energy,2014,39(35):20197-20206.
[15] DANTZIG G B,RAMSER J H.The truck dispatching problem[J].Management Science,1959,6(1):80-91.
[16] SHERBENY N A.Vehicle routing with time window:an overview of exact,heuristic and metaheuristic methods[J].Journal of King Saud University(Science),2010.22:123-131.
[17] 张文修.遗传算法的数学基础[M].西安:西安交通大学出版社,2000.ZHANG Wenxiu.Mathematical foundations of genetic algorithms[M].Xi’an:Xi’an Jiaotong University Press,2000.
[18] AHMED M,ZHENG Y,AMINE A,et al.The role of artificial intelligence in the mass adoption of electric vehicles[J].Joule,2021,5(9):2296-2322.
[19] DOS SANDOS E,RYUHEI S,KISU K,et al.Explore the ionic conductivity trends on B12H12 divalent closo-type complex hydride electrolytes[J].Chemistry of Materials,2023,35:5996-6004.
[20] DING R,YIN W,CHENG G.Effectively increasing Pt utilization efficiency of the membrane electrode assembly in proton exchange membrane fuel cells through multiparameter optimization guided by machine learning[J].ACS Applied Materials &Interfaces,2022,14(6):8010-8024.