Citation format:LI Zhenxin, XIONG Ling, CHENG Junsheng, et al.Winding Electromagnetic Design of Induction Electromagnetic Propeller[J].Journal of Ordnance Equipment Engineering,2020,41(1):178-183.
感应电磁推进器绕组电磁设计
感应线圈型电磁推进装置是一种重要的电磁推进方式,具有推力大、加速快、非接触等特点[1]。同步线圈推进器一般采用分立的多级驱动线圈,单相激励工作,该种线圈推进器需要开关动作与次级精确同步,控制和功率调节系统较为复杂[2]。且同步线圈推进器加速度小,不利于短程加速。传统的异步线圈型推进器使用圆筒形线圈作为其激励线圈,该种全封闭式的激励线圈限制了动子形状,迫使动子必须也为圆筒形。对一些大型非圆筒状的抛体,比如无人机、舰载战斗机等电磁推进,需要对传统的圆筒型线圈推进器的初级结构进行改良。由双边直线感应电动机驱动的轨道交通车辆多采用短初级结构,其制造成本低但推进速度小[3],在电磁推进系统中,由于要采用大功率脉冲的方式供电,采用短初级结构在高速运行的初级绕组必须通过滑动电刷或者移动电缆馈电,成本高,可靠性和安全性低[4],而长初级结构不存在这种问题。美国舰载的电磁炮装置就使用了双边直线结构,2015年,美国海军在福特号航母上面进行了电磁弹射实验,成功弹射出一个重量超过36吨的物体,同年11月,美国装载有电磁推进装置的驱逐舰成功下水。标志着电磁推进技术正式在军事领域得到应用[4]。
在电磁推进器电磁结构设计方面,中科院电工所闫萍教授等[5]以及南京理工大学等均对轨道式推进器炮管形状进行研究,西南交通大学王豫教授等[4,17]则对多极距型推进器的炮管构型进行结构参数分析。而基于上文阐述的各类原因,本文将开展对感应电磁推进器初级绕组形状的优化设计,满足对不规则抛体的短程高速推进要求[6]。基于双边电机的结构形式[8,15],有一种将封闭的圆筒型改为一组两边相对的开放式双边结构[3]。在此基础上,本文提出了一种不同于双边型与圆筒型的半开放式初级线圈结构,该结构弥补了双边型漏磁大与圆筒型动子结构单一的不足[9-11]。对“T”字型和“U”字型的推进器在绕线方式、电磁场分布、动子推进方向受力、出口速度、推进效率等方面进行比较分析。本文仅研究两种结构的推进器在推进方向上的性能指标,未涉及垂直推进方向上相关参量的优化与分析。
1 物理模型
1.1 推力方程
本文所介绍的感应电磁推进器中,铝制的次级线圈置于初级线圈内部,受到初级线圈的磁场激励而感生涡流,继而受力运动。由于驱动线圈固定不动,次级受到推进方向的推力而前进,现用有限元割分的方法将次级划分为多个小的导体片,先计算出每个小导体片上的推力,然后进行叠加,从而求出整个次级所受到的推进力[13-15]。
根据安培力定律,次级线圈的推进方向受力为
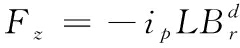
(1)
其中:ip为次级分片上的电流; L为次级分片的周长;![]() 为驱动线圈在次级线圈上产生磁场的径向分量。
为驱动线圈在次级线圈上产生磁场的径向分量。
对该模型进行有限元分析,该模型如图1所示。
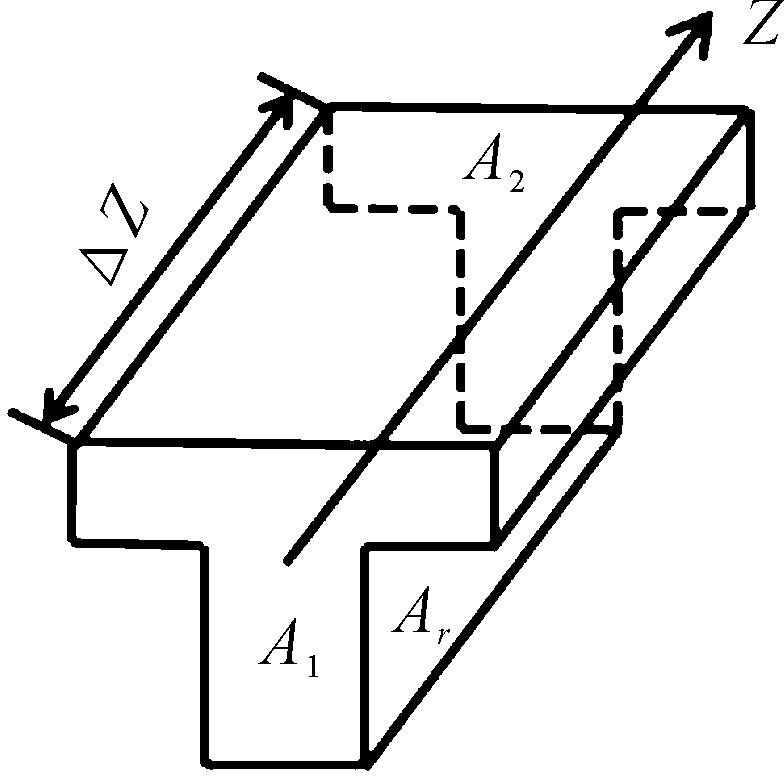
图1 次级导体分片示意图
根据磁通连续的原理,体磁通Φt为
Φt=∮A1B·dS+∮A2B·dS+∮ArB·dS
(2)
则可以得出驱动线圈在次级线圈上产生磁场的径向分量:
(3)
其中:Z为两个线圈之间的轴向距离;![]() 为两线圈间沿Z向的互感梯度。
为两线圈间沿Z向的互感梯度。
若含有由Nd个初级线圈和Np个次级导体片,则次级沿推进方向所受到的合力为
(4)
1.2 推进效率方程
推进效率η为次级线圈的动能增量与系统总输入能量的比值,本文只针对第一段加速进行研究,次级在开始第一段瞬间表面还没有产生感应电流,因此次级此时储能Wm=0。
推进效率η:
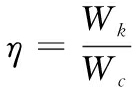
(5)
其中:Wk为第1段的动能增量;WC为电容储能,基于以上物理方程可知,次级沿推进方向所受到的推力与驱动线圈在次级线圈上产生的径向磁场![]() 以及初、次级中的电流成正比。而次级电流是由
以及初、次级中的电流成正比。而次级电流是由![]() 产生,
产生,![]() 是由初级线圈中的电流产生,初级线圈的电流是由电源系统产生的脉冲电流以及初级线圈的绕线方式决定的。
是由初级线圈中的电流产生,初级线圈的电流是由电源系统产生的脉冲电流以及初级线圈的绕线方式决定的。
2 系统构成
2.1 脉冲电源和驱动线圈连接方式
本文所提到的电磁推进器使用电容器储能式脉冲功率电源供电,利用脉冲电容器的大功率输出特性,满足电磁推进的高功率要求。采用3组脉冲电源模块配合工作,为异步控制电磁推进器供电。每组脉冲电源模块由脉冲电容器组、大功率晶闸管放电开关、续流二极管、触发与保护系统、电流测量系统等构成。
由式(4)可知,次级所受推力与初、次级的电流有关,因此初级线圈的连接方式将会影响次级受力。驱动线圈的连接方式分为串联和并联两种,图2、图3所示为单段6个驱动线圈的系统电路模型。
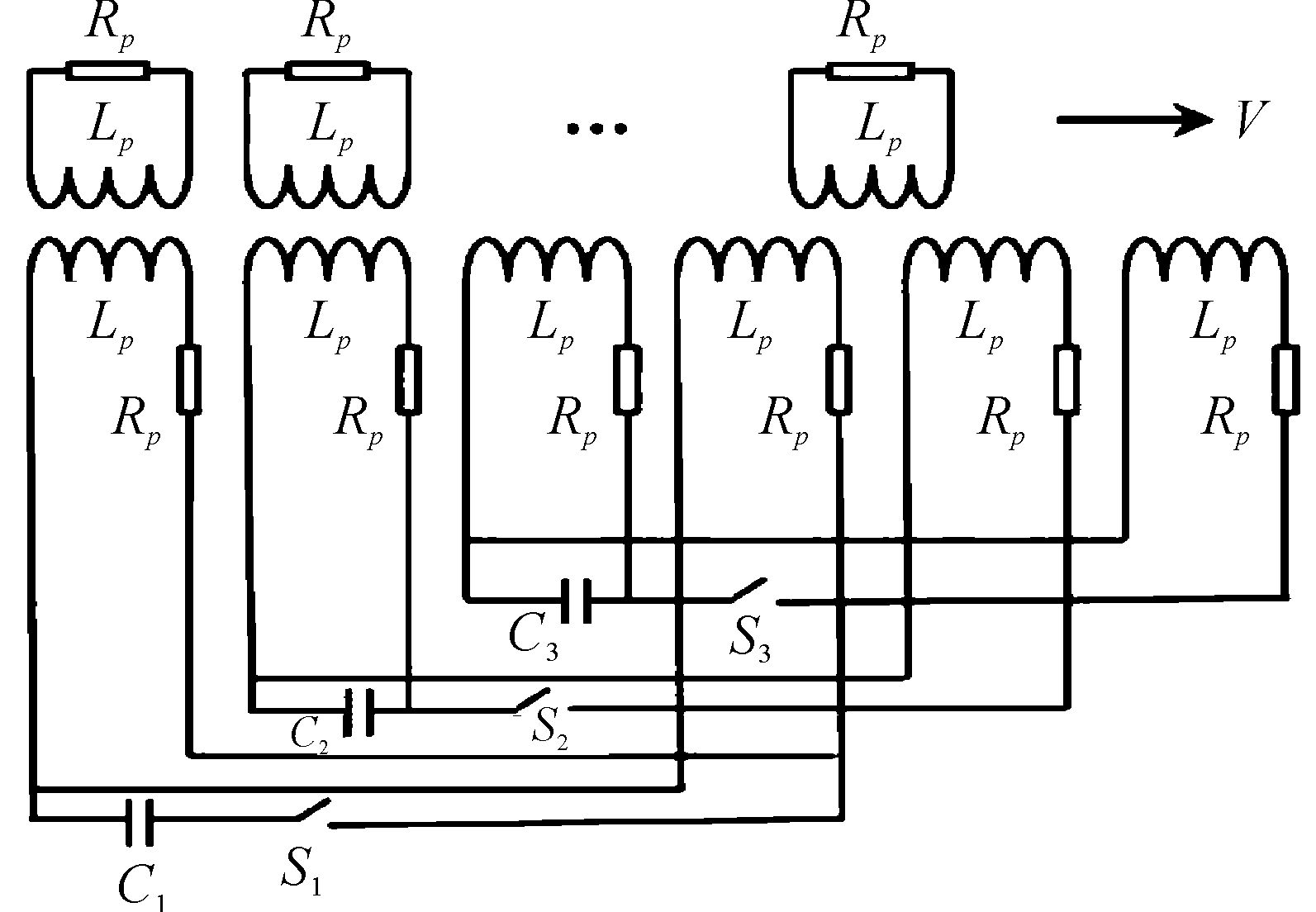
图2 电容式电磁推进器并联供电电路示意图[12]
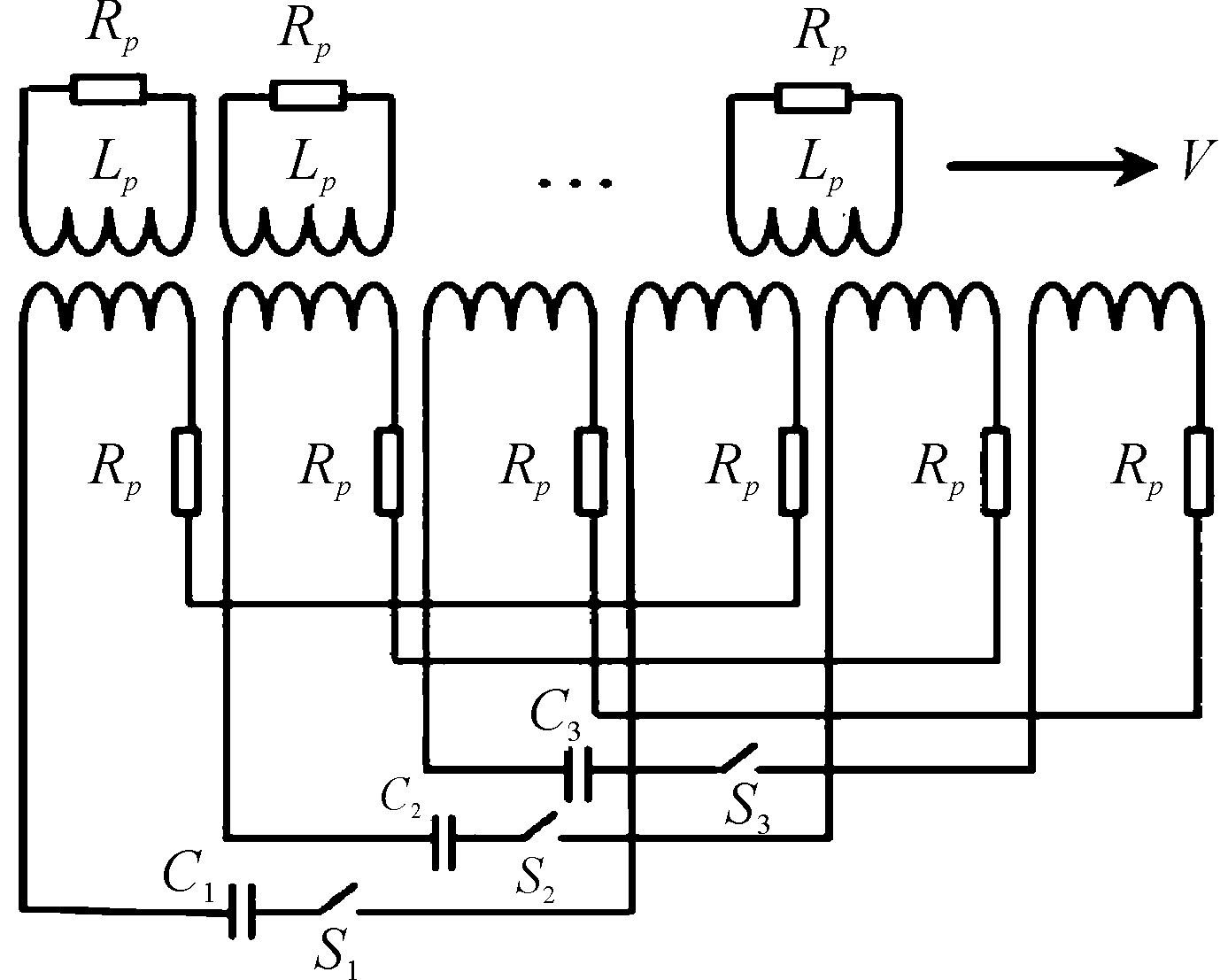
图3 电容式电磁推进器串联供电电路示意图[12]
本文的两种驱动线圈结构分别采用串联和并联两种方式供电并进行仿真模拟。
2.2 初级绕组模型建立
本文基于双边电机的结构形式,借鉴了可以搭载抛体的 “T”字型次级结构,但该种T字结构与传统的圆筒形电磁推进器相比,磁路开放性较强,漏磁大,因此在双边“T”字型推进器的基础上加以优化,提出了一种半封闭式的“U”字型结构。根据预设的1 kg、100 m/s的推进要求,核算能量利用率,从而得出电压与电容值范围,并估算出脉冲电源的峰值电流,由该电流推导出初级绕组的匝数,计算出初级的线宽以及极矩等参数。现对“T”字型推进器与“U”字型推进器进行建模仿真。
如图4所示为一种“T”字型的双边电磁推进装置[16-17],其中两边深色部分为其铜制的初级绕组线圈,铜线圈使用环氧FR4材料做为骨架,起到支撑、绝缘的作用。
图4中浅色“T”字型装置为带有装载平台的动子,其竖直部分在定子(激励线圈)产生的磁场中受到洛伦兹力作用而向前运动,水平的装载平台可以用来装载不同形状的抛体,使抛体与动子(感应线圈)一起运动。
如图5所示为一种“U”字型的电磁推进装置,其中深色部分为其初级绕组线圈,浅色“U”字型装置为带有装载平台的动子,其各部分作用以及推进机理均与“T”字型推进器相同。四种推进器的结构参数见表1。

图4 “T”字型电磁推进器模型图(不含骨架)
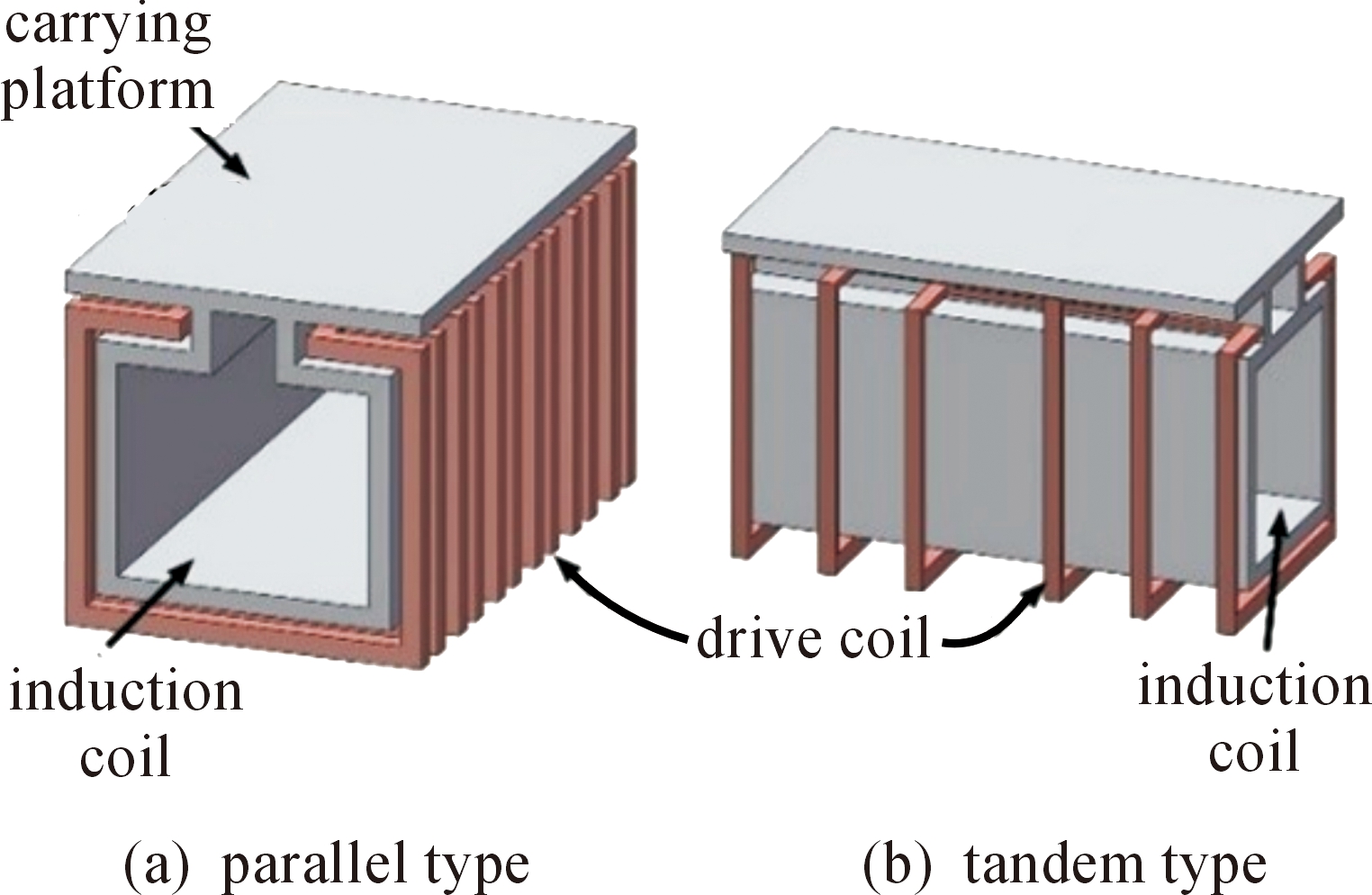
图5 “U”字型电磁推进器模型图(不含骨架)
3 建模仿真与对比分析
基于以上分析,结合预设指标估算出电容与电压的取值范围,在此范围内对两种结构的推进器进行了大量的计算仿真,表2中列出了最优组合值。通过对比发现推进1 kg动子时,两种推进器在5 000 V左右的电压下可获得最优的速度曲线。现对本文的4种推进器的推进效率进行计算、比较,本文推进器绕组匝数均设置为14匝,通过调整匝数可增加其推进效率。
表1 四种推进器结构参数
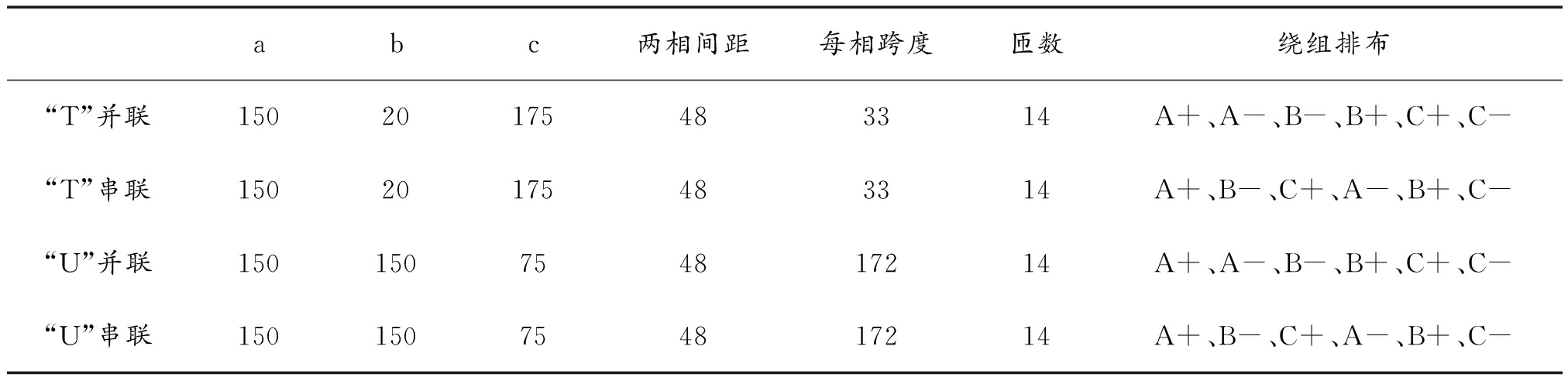
其中,a为铜线圈高度,b为铜线圈宽度,c为动子高度。
表2 推进器电参数

对比表格数据:串联式绕组的推进效率明显高于并联式绕组,说明串联式绕组的能量利用率高;由于串联分流,使串联式推进器的峰值电流明显小于并联式,脉冲电容供电的电磁推进器对大功率放电开关的要求很高,电流峰值越小,开关的可靠性就越高,因此在运行可靠性上,串联式推进器优势更明显;“U”字型推进器的效率和出口速度均高于“T”字型;串联式推进器所需的电容容量小于并联式,由于脉冲电容的体积大质量重,所需电容量越少的推进器的实用性更强。综上,“U”字型串联式电磁推进器更具有优势。
3.1 “T”字型推进器仿真分析
对两种T字型的电磁推进器进行建模仿真,感应型电磁推进装置的推进原理与感应电机类似,驱动线圈产生的磁场与感应线圈中的感生磁场所围成的平行四边形面积即为转矩,电磁推进器中驱动线圈被固定,转矩即为感应线圈所受到的推力。选取推进过程中磁场最大与最小时刻的磁场云图,如图6所示。并联与串联式推进器在推进过程中的推力曲线如图7所示。
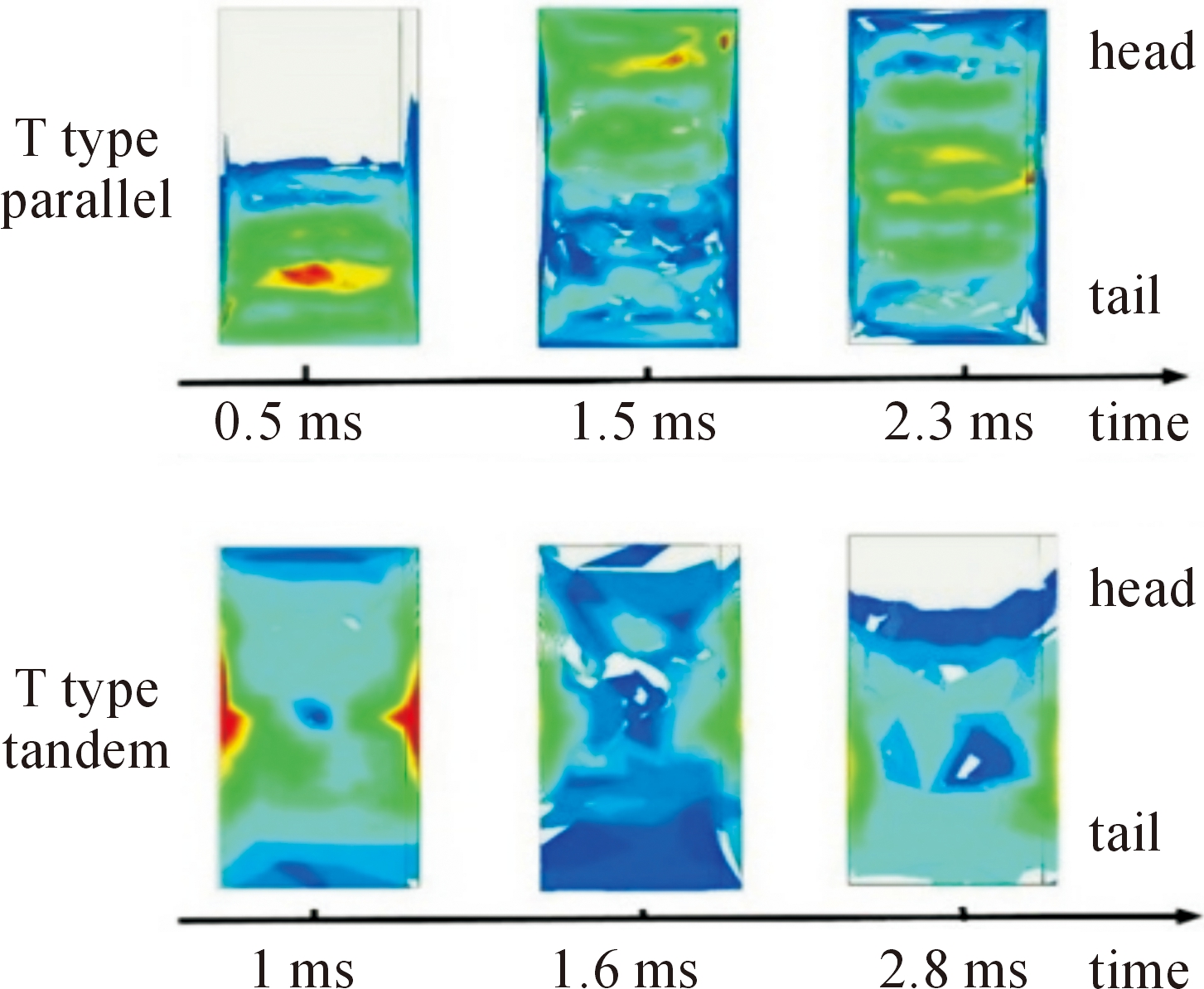
图6 “T”字型电磁推进器动子磁场云图
1.5 ms时,“T”字型并联推进器动子受到的感应磁场与激励磁场的矢量平行四边形面积最大,沿推进方向向前,此时动子的感应磁场为推进过程中的最大值,结合推力曲线可以看出,此时动子的推进力也为最大值。0.5 ms处,虽然动子的感应磁场模值高于1.5 ms处的磁场模,但它与激励磁场的叉乘积方向为推进方向的反方向,因此此处的推力为负值,这与并联绕组的排布有关。
对于串联式推进器,电源系统爆发式地向驱动线圈提供一个脉冲大电流,而后此电流又迅速衰减,于是在1ms时动子内迅速感生出了推进过程中的最大磁场,随后各相脉冲电流注入驱动线圈,但此时动子内已经有了感生涡流,所以第一次磁场峰值过后,第二次的峰值将低于第一次,在推力曲线中也可以看出这种走势。磁场与推力曲线的走势还与绕组的排布有很大的关系,现结合速度曲线对其进行分析比较。“T”字型串联与并联推进器速度曲线如图8所示。
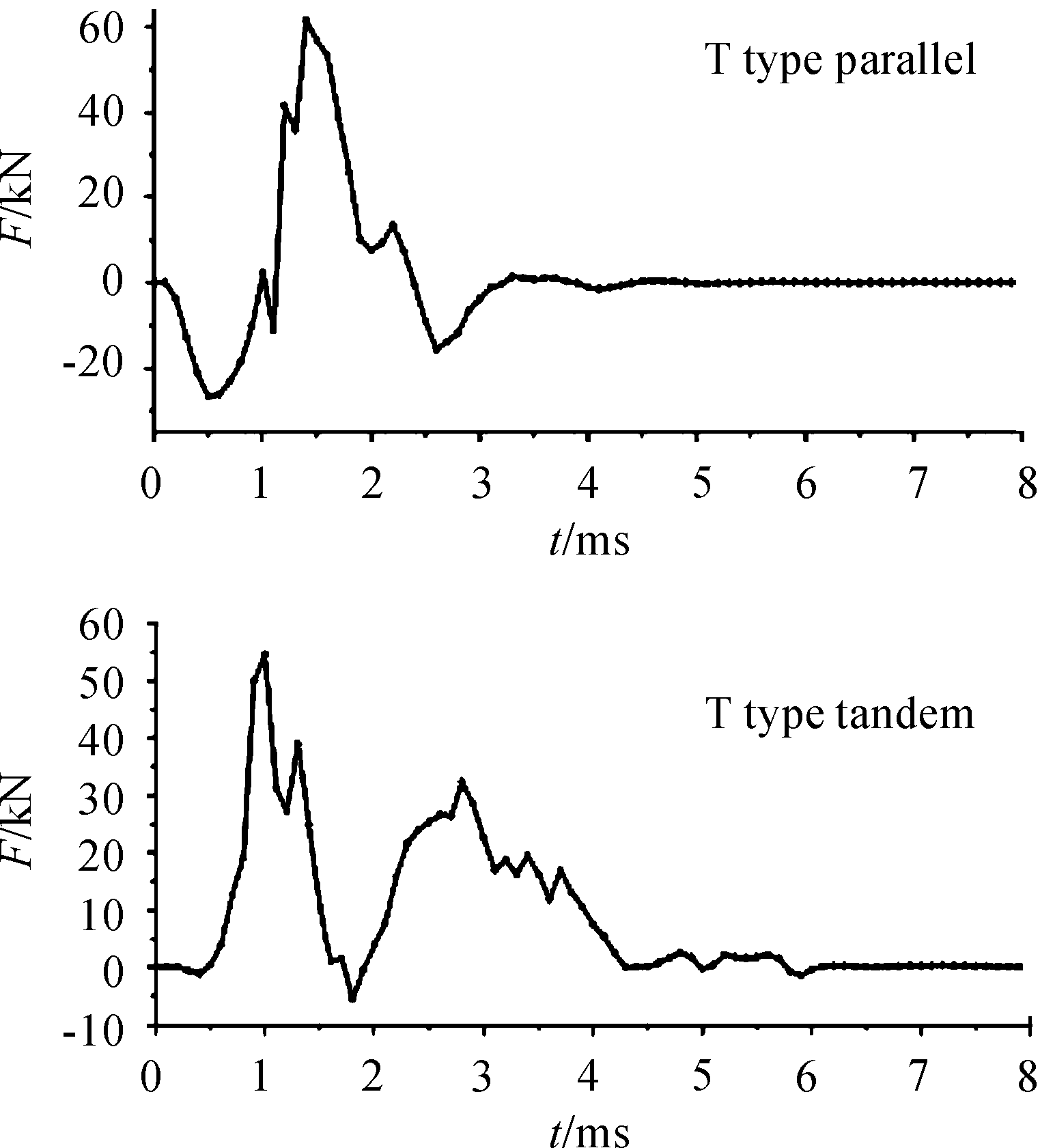
图7 “T”字型电磁推进器推力曲线
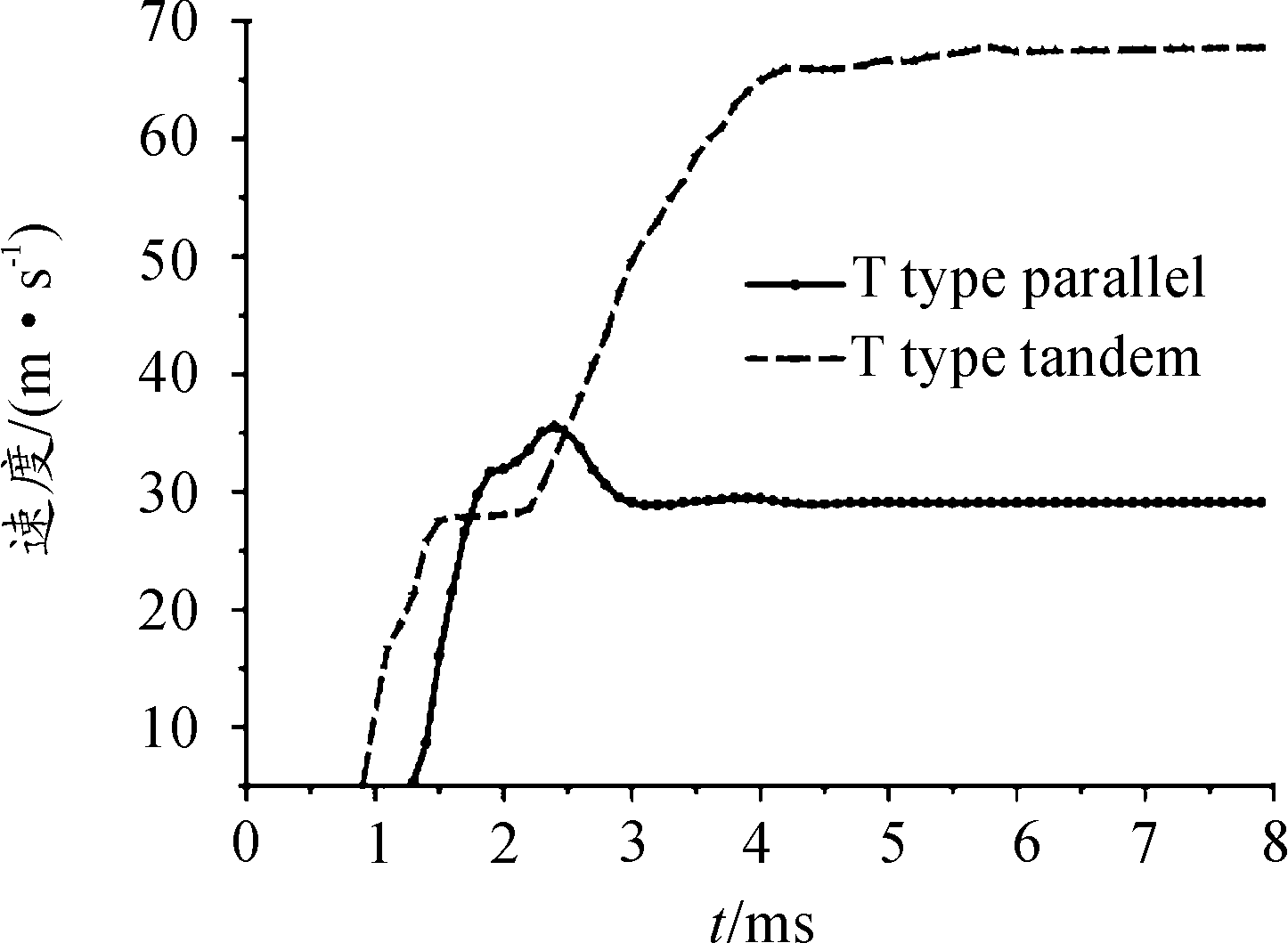
图8 “T”字型电磁推进器速度曲线
通过对比发现,串联与并联式推进器动子受力曲线走势明显不同,因为串并联三相绕组的排列方式不同,见表1。
结合磁场云图与推力曲线可以看出,“T”字型并联推进器动子在推进初期所受到感应磁场与激励磁场所组成的矢量力方向沿推进方向的负方向,即并联绕组排列方式使并联式推进器在推进初期存在一个反向推力。在脉冲电源激励下,A、B、C三相按照预先设置好的脉冲时序依次通入电流,推进开始时,动子在受到A+相产生的推力时,同时受到A-相的拉力,脉冲电源的爆发式放电导致动子在推进开始时受到的拉力大于推力,合力为负。随着ABC三相均通入电流之后,系统能量逐步转换为动子的动能,使动子前进。 串联绕组激励下的动子经过两段加速,在1.8 ms左右匀速前进,因为此时动子尾部离开了C+相,动子不再受A+、B-、C+相的磁场,且C+与A-的距离大于三相之间的距离,此时动子所受推力急剧下降。而进入到下一段加速段内,动子再次受到与第一段相同的推力作用,加上动子此时储存了部分动能,第二段加速度更高,最终加速至出口速度。从速度曲线图中可以看出串联式推进器速度曲线较并联绕组的速度曲线平缓,且其最终的出口速度高。
3.2 “U”字型推进器仿真分析
对两种“U”字型的电磁推进器进行建模仿真,其推力产生原理与“T”字型相同,选取推进过程中磁场最大与最小时刻的磁场云图,如图9所示。
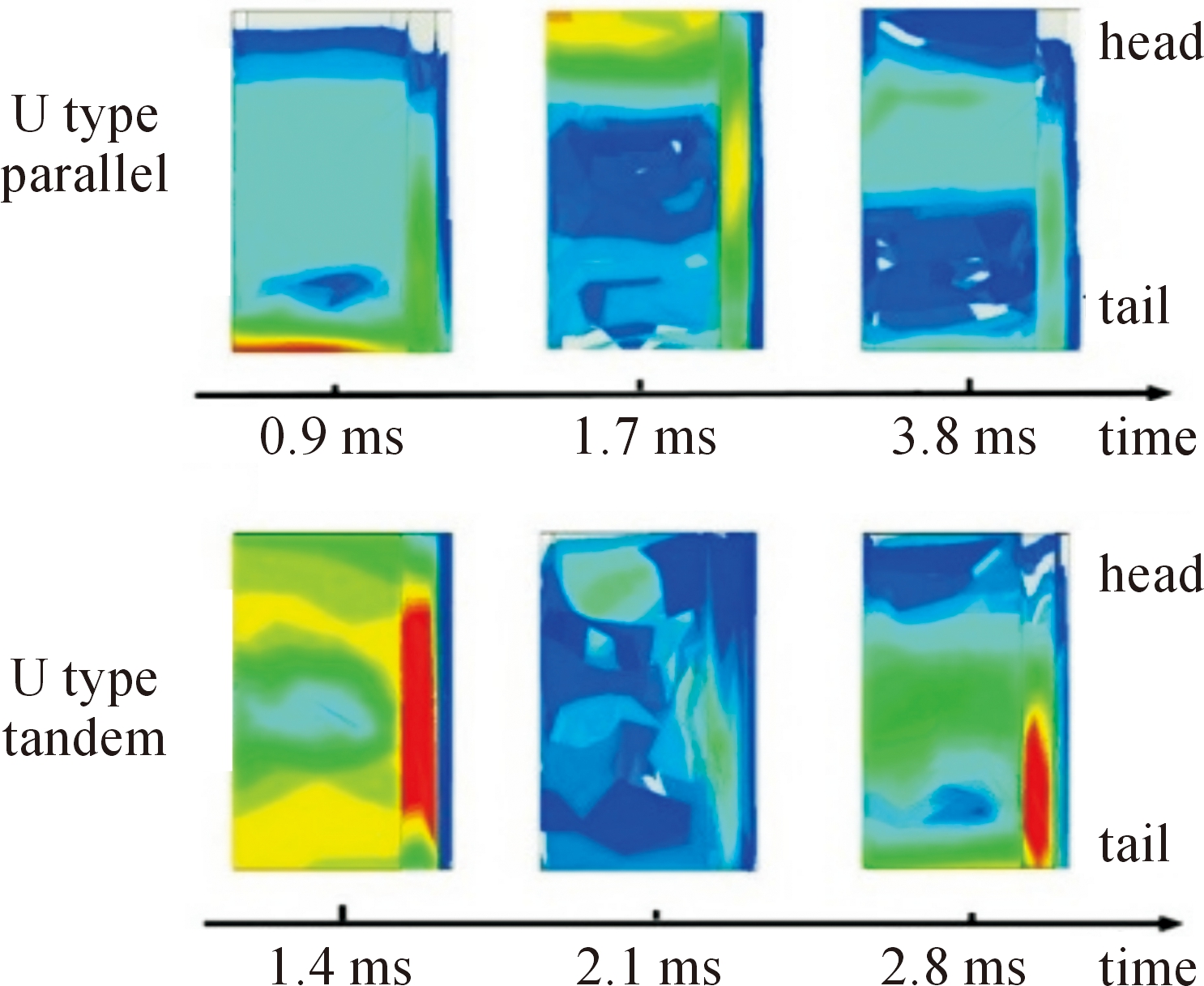
图9 “U”字型电磁推进器动子磁场云图
由式(3)、式(4)得:动子磁场与推力均与电感梯度和电流有关,电源电压相同时,串联绕组的互感梯度高于并联绕组,对比上图可得,串联式推进器的磁场明显强于并联式,串联式推进器的动子在推进初期感生的磁场明显高于并联式。两种绕组形式的推力曲线如图10所示。
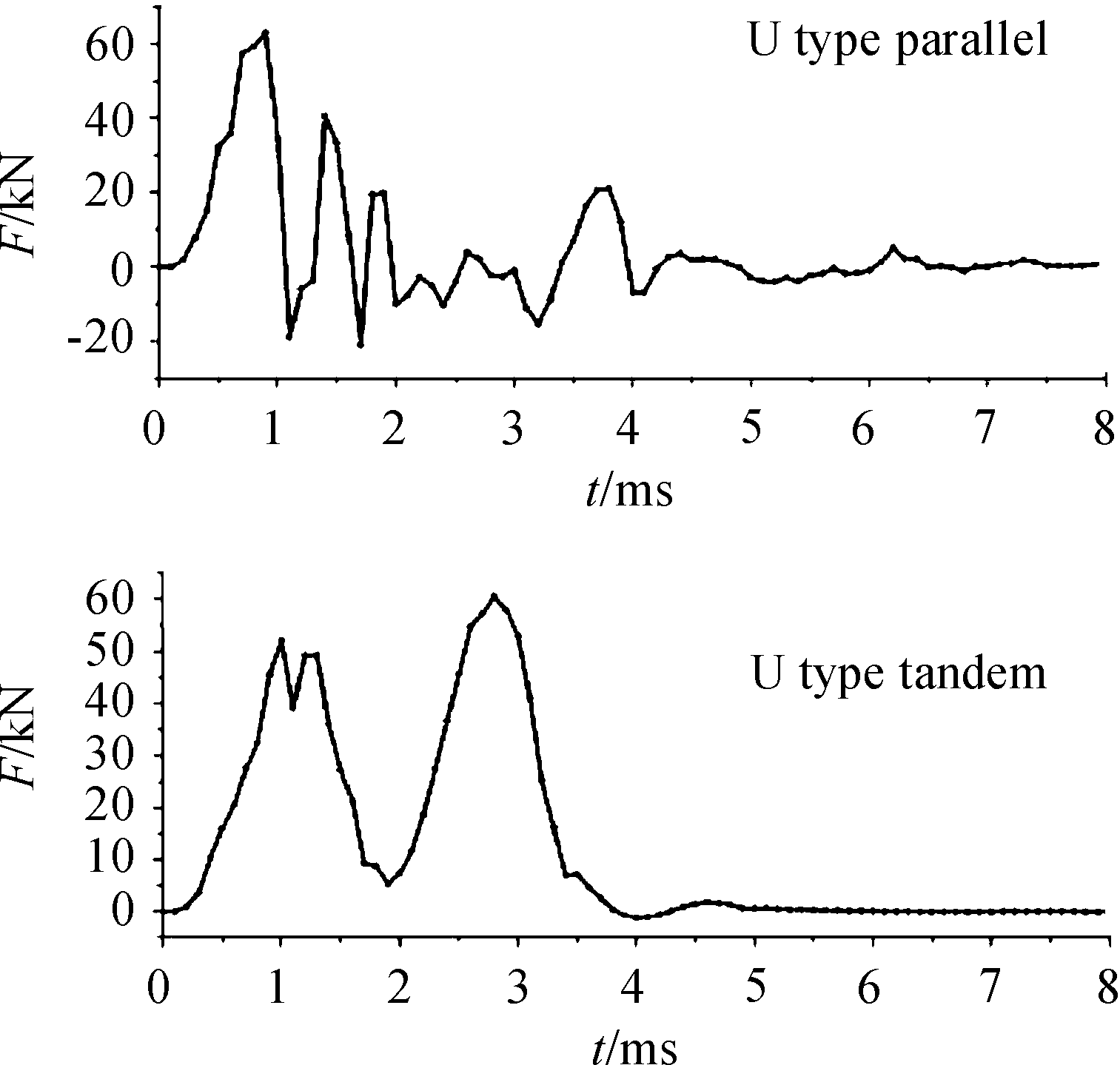
图10 “U”字型电磁推进器推力曲线
通过式(1),动子所受推力的模值正比于动子中的感生磁场,串联式推力曲线与磁场云图对比可以看出,串联式推进器在1.4 ms处为磁场的一个峰值,此时的推力也达到一极大值,2 ms左右磁场进入低谷,此时的推力也达到极小值。对比上示两图,并联式推进器的推力震荡很大,原因与“T”字型相同,是由并联绕组排列方式造成的,这将导致动子的加速度时正时负,速度不断震荡。串联与并联式推进器的推进速度曲线如图11所示。
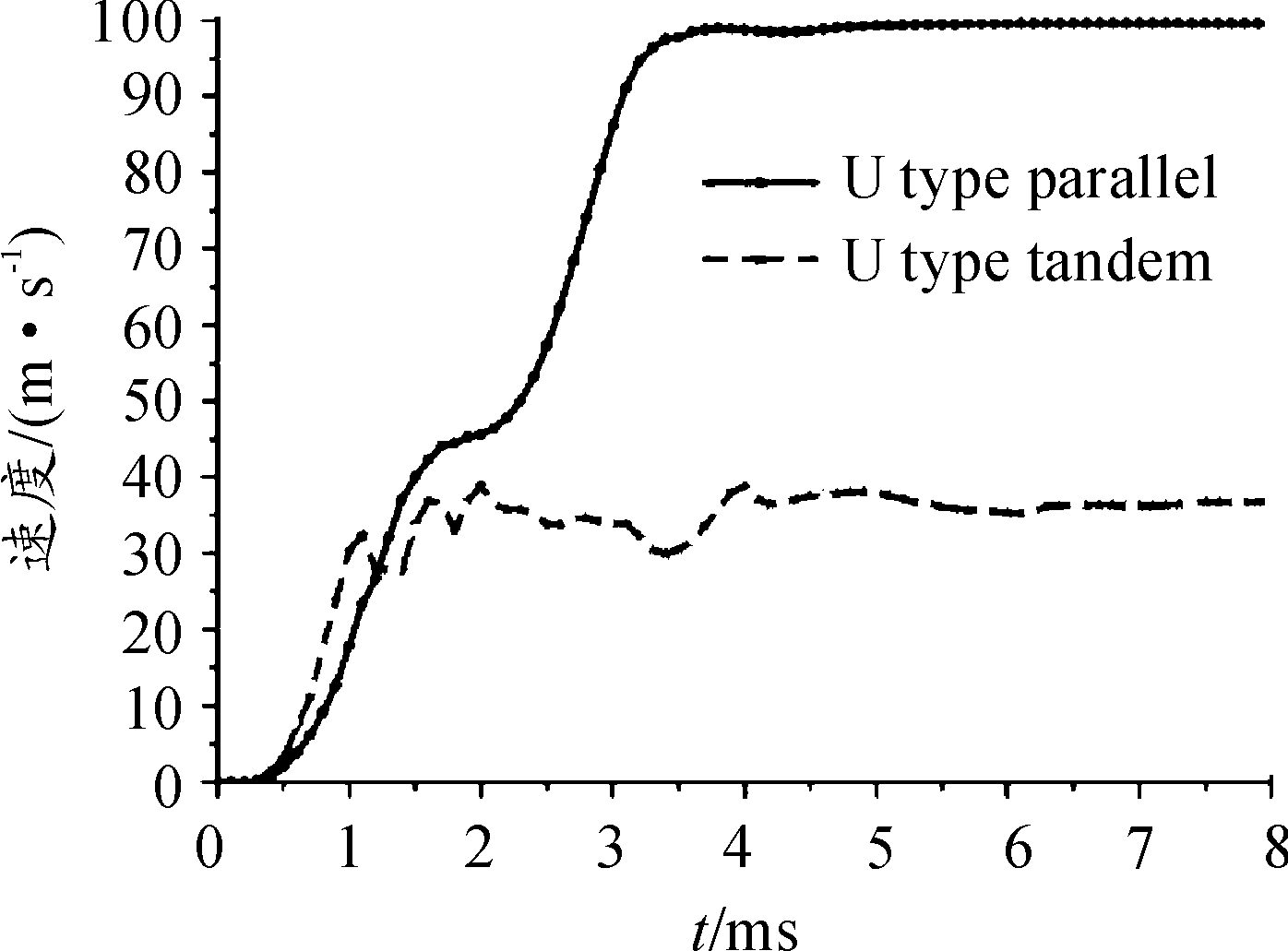
图11 “U”字型电磁推进器速度曲线
通过对比速度曲线可以发现,“U”字型电磁推进器并联绕组的速度曲线震荡很大,与上文的分析相吻合。串联式推进器对动子有两个推力峰值,因此串联绕组激励下的动子经历了两段近似恒加速度加速,在推力极小值附近加速度几乎为零,动子做近匀速运动。综上,串联绕组的速度曲线较并联绕组的速度曲线平缓,无震荡,且其最终的出口速度高。
3.3 两种结构串联式绕组对比分析
上述证明在两种结构的推进器中,串联式推进器的推进性能优于并联式,对比图8与图11中两种结构的串联速度曲线可以看出,“U”字型串联式推进器的最终推进效果优于“T”字型;且“U”字型的电磁利用率高。沿动子尾部,在垂直推进方向取一截面,分别选取动子开始运动的时刻,绘制两种结构的串联式推进器的电磁线分布,如图12所示。
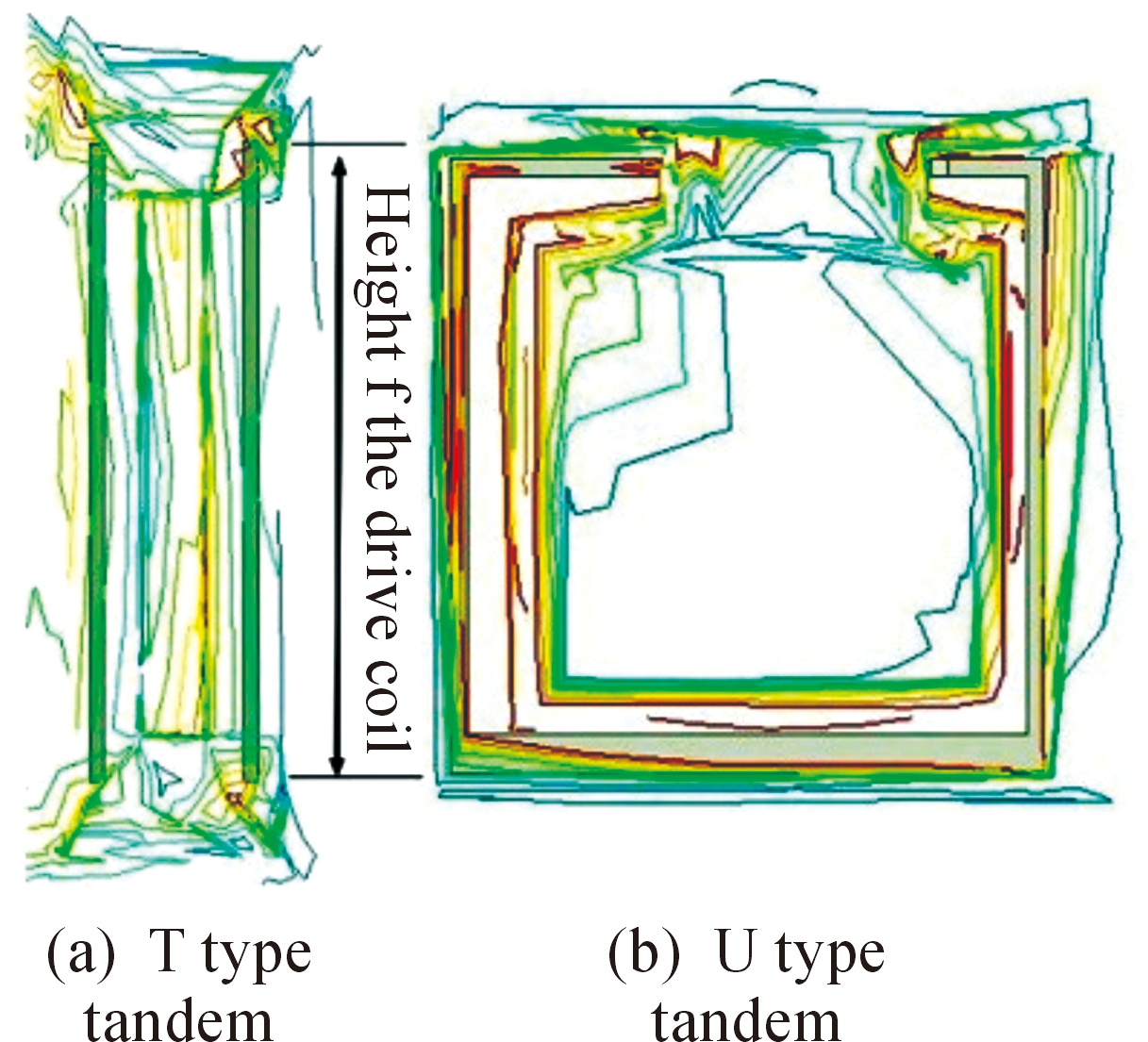
图12 两种串联式推进器磁场等值线分布
图12中已标出串联式初级绕组高度。从图12可以清楚地看出,“T”字型推进器的漏磁大于“U”字型。“U”字型推进器的半封闭结构可以将驱动线圈所产生的磁场禁锢在其内部,而“T”字型推进器的开放式结构在驱动线圈端部产生大量漏磁,且由于驱动线圈端部的曲率高,使得端部的磁场高于两平板之间的有效磁场,造成了能量损失。
综上,“U”字型串联式推进器的漏磁小,能量利用率高。
4 结论
1) 对驱动线圈采用串联的方式供电时,推进速度为并联式供电的2~3倍,推进效率为并联式13~25倍,且推进稳定性强,推进速度曲线无明显波动。
2) “U”字型驱动线圈在推进抛体时,与“T”字型驱动线圈相比,推进磁场强,推进效果好,能量利用率高。
3) “U”字型推进器的初级绕组漏磁少,可以将磁场禁锢在初级绕组内部。而“T”字型推进器在初级绕组端部漏磁现象严重,使得其有效磁场小。
4) 电压相同的情况下,串联式推进器所需的电容容量低于并联式,但串联式推进器的最终出口速度反而高于并联式推进器。说明串联式推进器的经济性和实用性均优于并联式推进器。
[1] 路梅,蒋丽萍.低速小过载异步感应线圈炮的仿真研究[J].科技创新与应用,2019(2):13-16.
[2] 王莹,肖峰.电炮原理[M].北京:国防工业出版社,1995.
[3] 龙遐令.直线感应电动机的理论和电磁设计方法[M].北京:科学出版社,2006: 125-134.
[4] 隆小飞.多极矩电磁推进系统效率影响因素的综合分析和扭转特性研究[D].成都:西南交通大学,2017.
[5] 周媛,严萍,袁伟群,等.电磁轨道发射装置中导轨几何参数对电感梯度的影响[J].电工电能新技术, 2009.
[6] 赵科义.电磁弹射原理与技术[M].北京:兵器工业出版社,2015.
[7] ZHANG Y J,QIN W N,RUAN J J.Analysis of Cumulative Damage Failure for Driving Coil in Coilgun[J].IEEE Transactions on Plasma Science,2015,43(5):1254-1260.
[8] 张志华.分段式长初级双边直线感应电机特性研究[D].北京:中国科学院大学,2014.
[9] DU Y M,JIN N Q.Research on Characteristics of Single-sided Linear Induction Motors for Urban Transit[C]//2009 International Conference on Electrical Machines and Systems (ICEMS 2009).
[10] 刘希军,朱新宇,刘小涵.电磁弹射用变极距直线感应电机设计研究[J].微特电机,2018,46(11):25-28,34.
[11] 卢琴芬,方攸同,叶云岳,大气隙直线感应电机的力特性分析[J].中国电机工程学报,2005, 25(21):132-136.
[12] 李献.直线感应线圈推进装置的分析与实验研究[D].北京:中国科学院研究生院,2012.
[13] 付磊.线圈感应型电磁推进系统加速电枢的研究[D].成都:西南交通大学,2011.
[14] 汪治全,隆小飞,严仲明,等.多极矩电磁推进器级间耦合特性分析[J].微电机,2016,49(11):24-27,50.
[15] 许金,聂世雄,马伟明,等.无槽双边长定子直线感应电动机磁路计算方法[J].中国电机工程学报,2016,36(10):2793-2799.
[16] GANESH V S,KADAVERLA A, LENIN N C.Design,Development and Electromagnetic Analysis of A Linear Induction Motor[J].Applied Mechanics and Materials,2016,4340(1704):794-798.
[17] 汪治全,王豫,严仲明,等.基于均匀设计的单级多极矩电磁推进器结构参数优化[J].兵工学报,2016,37(4):744-750.
