【信息科学与控制工程】
基于特征优化与最优拼接缝的视差图像拼接
图像拼接技术是将具有重叠区域的多幅图像拼接成一幅大视场的全景图像，在摄影测量、遥感监测、军事侦察等领域广泛应用[1]。图像拼接主要包括预处理、图像配准和图像融合3个阶段。传统拼接方法[1]常采用特征匹配建立全局单应变换完成图像的局部对齐，对于相机光轴固定不变或者拍摄场景处于同一平面的图像具有不错的效果，而对于复杂场景或者具有视差的图像，采用单一的单应变换往往会产生重影和透视失真的情况。为了解决复杂的视差图像拼接问题，众多学者及团队致力于在三类方法上进行拼接工作的改进与完善，一类是基于局部自适应对齐模型的拼接方法，如Gao等[2]将目标场景划分成前景端和背景端，使用2个单应性矩阵进行非线性对齐，但是这种方法受限于只能在没有局部透视的情况下才有效；Zaragoza等[3]提出基于移动直接线性变换的APAP(As-projective-as-possible)对齐方法，通过建立局部单应矩阵解决局部偏差问题；Lin等[4]基于APAP的局部单应矩阵结合全局最优相似矩阵，平滑过渡重叠区域的透视变换，缓解非重叠区域的透视失真问题。一类是基于内容保留的拼接方法，Zhang等[5]通过结合单应矩阵与内容保护技术进行拼接，既保留了图像结构，又解决了视差引起的局部对齐问题；何川[6]在NISwGSP算法[7]的基础上提出了一种具有直线结构保护的拼接方法，在对网格进行相似性连续性约束的同时辅以直线结构约束，最后使用最小二乘法获得网格顶点集指导网格变形；一类是基于拼接缝的拼接方法，如Lin等[8]提出一种基于缝引导的局部对齐方法，首先利用特征点组成若干局部单应矩阵变形图像进行初步的配准，再使用结构保护和特征加权对局部配准进行不断优化，通过评价不同拼接缝效果，选择无缝配准效果最好的一组进行拼接。
目前，视差图像拼接因特征点配准误差大造成局部结构变形以及重叠区域纹路复杂度高出现重影等问题是学者重点研究问题，本研究提出结合RANSAC(Random Sample Consensus)[9]和正态分布模型的方法进行特征点筛选，同时改进图割理论[10]中能量损失函数，为损失函数添加新的约束条件，获得一条符合人眼显著性感知的最优拼接缝，最后采用多波段融合的方法进行图像融合，完成拼接工作。
1 特征细化理论
图像配准是图像拼接技术中关键的步骤，在特征检测和匹配过程中往往会出现外点保留较多、误匹配等现象。常用的外点移除方法是使用RANSAC进行迭代估计数学模型，剔除不满足此模型的外点，由于受迭代次数的影响以及对于不同拼接场景需要设置不同的阈值，RANSAC获得的匹配点依然会有大量外点存在以及部分内点被移除的情况。算法REW[11]将TPS(Thin Plate Spline)模型的系数分布服从正态分布并设计贝叶斯模型作为剔除外点的准则，本文采用文献[11]通过中心极限定理得到匹配点的投影误差服从标准正态分布这一准则，依据正态分布3σ定理，将分布在小概率事件中的匹配点进行剔除。
假设待拼接图像I0、I1，通过RANSAC获得匹配点为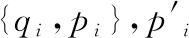
是由获得全局单应矩阵H在I0上的投影点，投影偏差
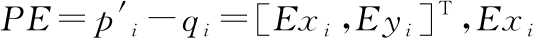和Eyi为x和y2个方向的投影偏差，假设事件Cxi={|Exi-μx|<nσx}，Cyi={|Eyi-μy|<nσy}，其中μ代表投影偏差的平均值，σ代表投影偏差的标准差，根据正态分布理论，因投影偏差分布符合标准正态分布，获得以下公式：
p(Cxi)=p{|Exi-μx|<nσx}=
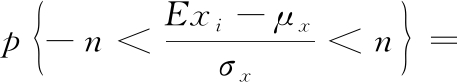
2φ(n)-1
(1)
p(Cyi)=p{|Eyi-μy|<nσy}=
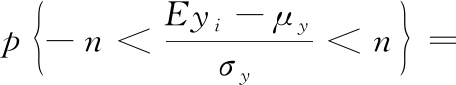
2φ(n)-1
(2)
其中Φ(·)代表标准正态分布。
当设置n=3时，由标准正态分布3σ理论可知，事件的概率p=2Φ(3)-1=99.73%，对于不满足此事件阈值的匹配点{qi，pi}进行移除。从几何原理上来讲，进行剔除的原理是如果一组匹配点的投影误差与附近其他匹配点的投影误差存在明显的不同，那么将它认为是外点，虽然这种情况下一小部分的内点可能被错误地删除，但不会影响最终的拼接质量。图1展示使用正态分布理论进行特征点优化的情况，所有彩色点为使用RANSAC后的匹配点，红色点为使用本文外点筛选理论删除的外点，绿色点是为最终保留的内点。
图1 外点筛选图
2 最优拼接缝寻找
基于缝切割的图像拼接方法在局部对齐上具有良好的表现，通过寻找不可见的拼接缝实现图像合理并且自然的缝合，图割理论被应用于有向图中寻找最少能量的最短拼接缝，取得良好的表现[5，8]。
2.1 缝切割方法
通过定义能量函数，将分割的代价依据权值来表达，能量函数定义成式3的形式，假设一组对齐图像为I0和I1，P为图像的重叠区域，整幅图像的标签L={0，1}，其中0对应图像I0，1对应图像I1，给重叠区域的所有像素p∈P分配一个标签以此获得标签集l={l1，l2，l3，…，lp}，当标签集为l时，图像的能量为
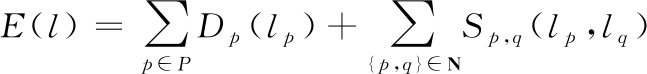
(3)
其中：Dp(lp)是数据项，代表为像素p分配标签lp的损失；Sp，q(lp，lq)是平滑项，代表为一对像素(p，q)∈N分配一组标签(lp，lq)的损失；N代表P*P像素邻域面。
传统缝切割方法中的数据项一般定义为
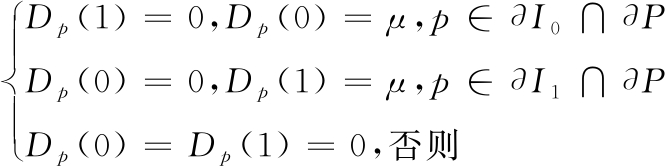
(4)
式中： μ代表较大的损失值；?It∩?P代表图像It(t=0，1)与重叠区域P的共同边界。
平滑项被定义为
Sp，q(lp，lq)=|lp-lq|(I*(p)+I*(q))
(5)
其中
I*(·)=||I0(·)-I1(·)||2
式中：I*(·)为2-范数，代表欧式色差距离指标，平滑项代表像素p与邻域中其他节点不连续的惩罚，如果p与q的差别越小，它们属于同一目标或者同一背景的可能性越大，对应的损失越大；如果像素p与q的差别很大，则说明2个像素位于目标和背景的边缘，被分割的可能性越大，损失能量越小。
2.2 改进能量函数的缝切割方法
1) 数据项的改进
文献[12]认为数据项的设定可以基于指定颜色的欧式色差距离、合成颜色的欧式色差距离、分布于图像直方图的最小或最大可能性、距离指定图像对应像素的欧式色差距离等多种形式，本文将缝切割中将数据项定义为
Dp(lp)=-▽I(lp)
(6)
lp代表为像素p分配lp的标签值，当赋值lp为1时表示使用p在图像I1上的梯度值，当赋值lp为0时表示使用p在图像I0上的梯度值。
2) 平滑项的改进
传统缝切割中对于平滑项只基于对颜色空间的考虑，缺少对于梯度空间的考虑，本文对于平滑项添加梯度值融合考虑，
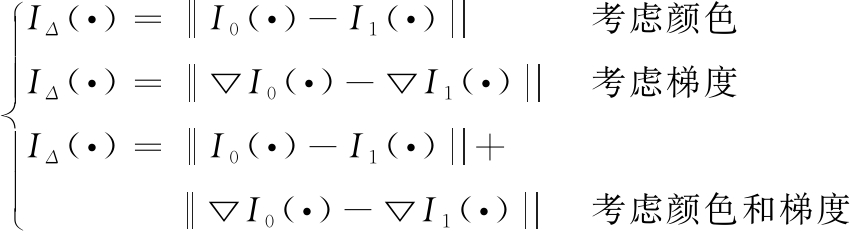
(7)
在添加梯度值考虑后平滑项形式
Sp，q(lp，lq)=|lp-lq|(IΔ(p)+IΔ(q))
(8)
其中
IΔ(·)=||I0(·)-I1(·)||+||▽I0(·)-▽I1(·)||
IΔ(·)中的第1个范数代表颜色空间的色彩强度的差值，第2个范数代表梯度空间的不同图像中相同点在水平和垂直方向的梯度差值。
同时为了增加对重叠区域重要目标的保护，也是基于人眼对图像中显著目标有着更高的关注度，本文为平滑项添加一个显著性权重
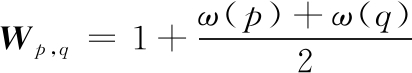
(9)
其中ω(·)代表P的平均像素显著性，通过文献[13]中的显著目标检测算法计算，为了避免最终的惩罚值过大，标准化Wp，q使其在[1，2]的范围内，Wp，q根据ω(·)会增加对Sp，q(lp，lq)的影响。
改进后的能量函数形式如下：
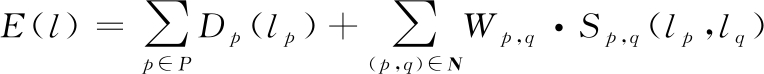
(10)
通过图割理论的最大流最小割[14]方法使能量函数最小化，即可找到一条对应的最佳拼接缝。
3 算法流程
本文算法的流程示意图如图2所示，具体内容如下：
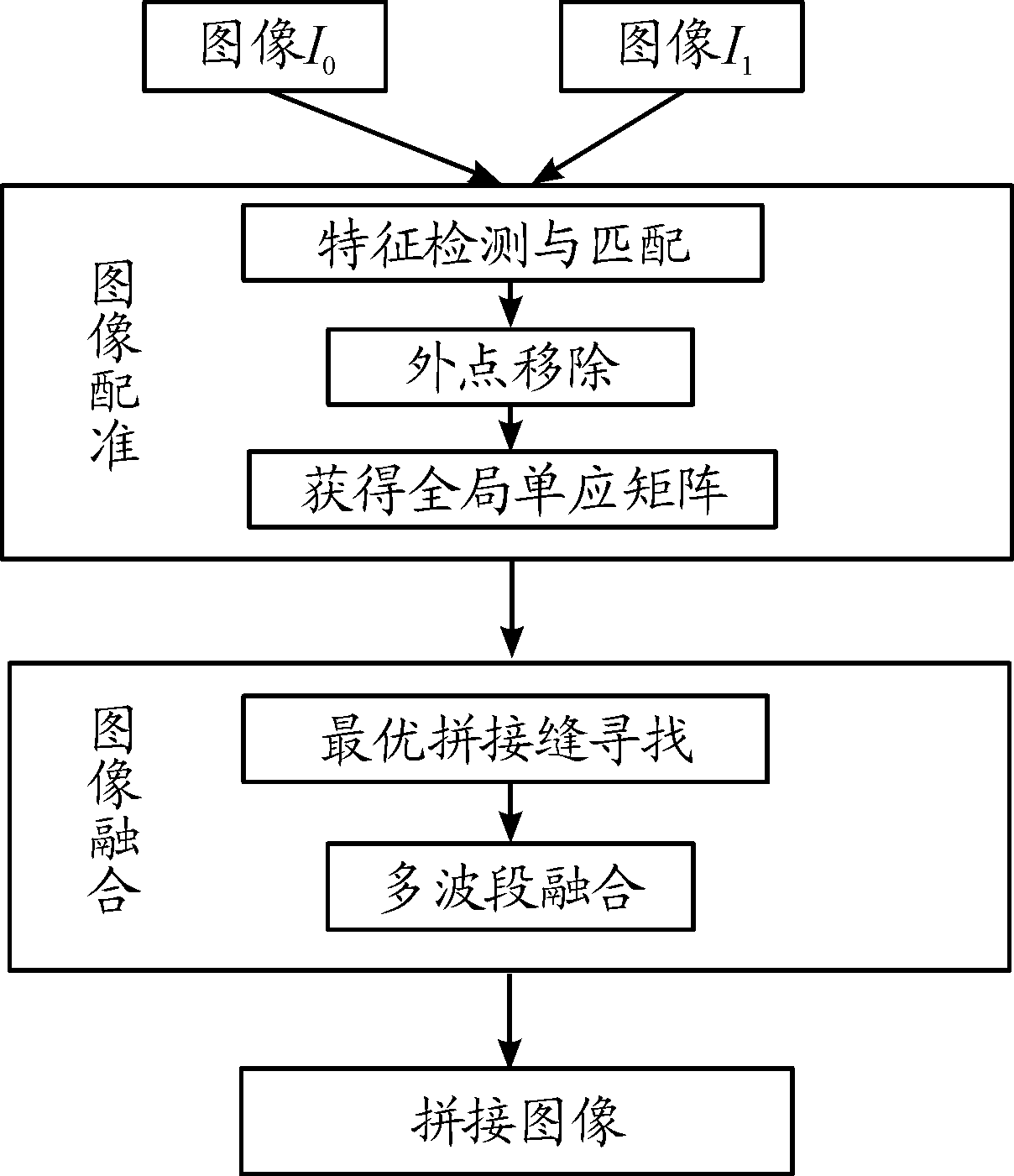
图2 算法流程框图
1) 首先对待拼接图像I0和I1使用SIFT(Scale-invariant feature transform)算法进行特征点检测，然后使用阈值εg=0.1的RANSAC算法进行初步匹配过程，利用RANSAC获得全局单应矩阵H计算匹配点的投影误差PE。
2) 依据本文提出的投影偏差PE服从正态分布这一准则，对匹配点进行再次筛选，得到优化的匹配点利用DLT计算新的全局单应矩阵Hnew，将目标图像I2利用Hnew变换到参考图像I1的坐标系中。
3) 获取拼接图像的重叠区域P，计算函数中数据项每个像素的损失Dp(lp)，计算平滑项中邻域像素的损失Sp，q(lp，lq)，使用显著目标检测算法计算ω，得到显著性权重Wp，q。
4) 利用图割理论最大流最小割方法最小化损失函数 E(l)，获得最优拼接缝。
5) 使用多波段混合的融合方法进行图像融合，得到最终拼接结果。
4 实验结果与分析
本文采用文献[5]中提供的2组图像作为实验图像进行实验，如图3所示，图像大小为1 000×662(宽×高)，利用Matlab R2018进行实验。
4.1 特征匹配实验
2组实验图像组如图3所示分别利用RANSAC和本文的外点筛选方法进行操作，从图中特征点匹配的结果可以看出，RANSAC方法保留了大量错误的外点，而本文利用提出的外点筛选准则进行错误外点的剔除，有效地保证了内点的保留，将偏差较大的错误匹配点进行删除，同时为了更加客观的表达本文方法在删除外点的有效性，采用统计所有匹配点在X和Y方向的偏差，并且提高评判标准将匹配点偏差的欧式距离小于5个像素的匹配点看作准确匹配点，并统计准确匹配点的数量，计算准确率，具体的实验数据如表1所示，从匹配点数量可以看出，本文方法保留有效匹配点，使得匹配点的数量降低，在偏差方面，图像组1和2在X和Y方向偏差总量大量减少，并且准确率分别提高了16.6%和13.1%。
表1 RANSAC和本文精匹配结果
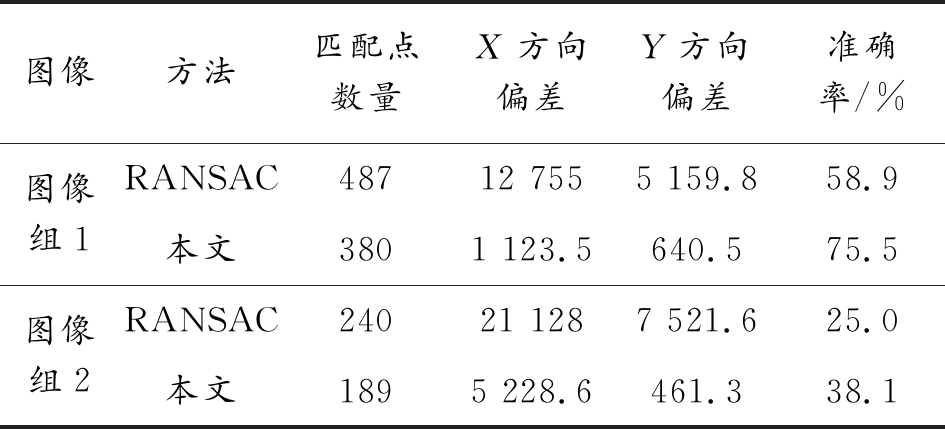
图3 外点筛选结果图
4.2 拼接缝搜索实验
采用传统的图割拼接缝寻找方法对比本文的拼接缝搜索方法，图4(a)中传统的拼接缝搜索方法可以完成对图像的基本对齐，但是在白色建筑物中间穿过，并且在与黄色建筑物的交接处发生局部的变形扭曲，黄色建筑物的墙体变形严重，图4(b)中本文的拼接缝可以较好地沿着白色建筑物的边缘进行分割，并且在拼接难度较大的两建筑物中间实现较好的分割，整体图像表现地更加自然真实；在第二组图像的拼接缝寻找中，如图4(c)、(d)所示，两条拼接缝的基本走向一致，但是在细节方面，本文的拼接缝在规避目标表现更好，并且在拼接难度较大的地面纹路处，传统拼接缝发生了扭曲变形，而本文的拼接缝保持了地面良好的纹路效果。
图4 拼接缝寻找结果图
4.3 拼接结果实验
在MTALAB R2018运行APAP以及本文算法，同时对比Microsoft ICE软件和文献[5]中算法的拼接结果，具体实验结果与分析如下:
1) 图像集1的拼接结果与分析
图像集1是两幅具有明显视差的图像，4种方法中，如图5所示，APAP算法在局部对齐上出现明显的重影和误对齐，可以看到在建筑物墙体边缘出现严重的变形，其他3种方法完成了较为准确的对齐，拼接效果基本满足普通需求，在一些细节方面，拼接结果图中采用红色矩形框进行标注的地方，ICE软件的拼接图中，墙体边缘产生严重变形，建筑物之间的空隙发生明显差异，信号灯灯柱位置出现误对齐，Parallax-tolerant的拼接结果中建筑物墙体间出现变形，信号灯灯柱也出现误对齐现象，本文方法完成了两张图像的整体对齐，在建筑物的墙体边缘和墙面纹理上都没有严重的变形，信号灯灯柱对齐，相比于其他3种方法，拼接效果更好。
图5 图像组1拼接结果对比图
2) 图像集2的拼接结果与分析
图像集2的两幅图像是具有复杂地面纹路、视差较大图像，拼接难度大于图像集1，如图6所示，在ICE的拼接结果中，为了对齐地面纹路，造成了卡车位置出现重影，图像的中间位置出现严重的变形，树木出现严重误对齐，APAP的拼接图中，在文中用红色矩形框进行标注，出现人的重影，并且在烟囱和蓝色玻璃建筑物边缘都发生不同程度的变形，Parallax-tolerant与本文的方法在图像上整体对齐，没有发生严重变形，但在红色矩形框标注的地面纹路和蓝色玻璃建筑物的墙体拼接上出现变形，本文的拼接结果整体完成良好的对齐，在上述的位置中表现效果均优于其他3种方法。
图6 图像组2拼接结果对比图
为了更加客观地描述拼接结果图的质量，本文采用文献[15]中提出的无参考图像的自然图像质量评价(NQIE)，该视觉评价方法符合人眼感官评价，图像获得分数越低，对应图像质量越好，表2为上述4种方法在2组图像集中的得分，在2组图像的质量评价中，本文的得分最小，代表图像质量最好。
表2 4种拼接方法评价得分情况
5 结论
本文提出一种基于特征细化和最优拼接缝寻找的视差图像拼接方法，采用投影偏差服从正态分布理论进行外点移除工作，优化了特征匹配结果，获得最优的全局变换矩阵，对图割能量函数中数据项采用梯度值计算损失值以及平滑项融合梯度值考虑并添加显著性约束，获得能够保护图像显著目标并且符合人眼感知的拼接缝，采用多波段融合方法，减少重叠区域的色差变化，实现平滑过渡。在图像特征匹配的质量和拼接缝寻找中，本文方法与传统方法对比明显占优，本文方法与APAP、ICE、Parallax-tolerant进行比较，在示例图像最终拼接效果更加自然、真实，有着较高的实用价值，但是本文算法在纹理不明显、视差较大的场景也出现过匹配误差较大、错位等现象，后续过程需要不断优化、改进。
[1] BROWN M，LOWE D G.Automatic Panoramic ImageStitching Using Invariant Features[J].International Journal of Computer Vision，2007，74(1):59-73.
[2] GAO J，KIM S J，BROWN M S，Constructing ImagePanoramas Using Dual-homography Warping[C]//IEEE Conferenceon Computer Vision and Pattern Recognition(CVPR).[S.l.]:[s.n.]，2011:49-56.
[3] ZARAGOZA J，CHIN T J，BROWN M S，et al.As-projective-as-possible Image Stitching with Moving DLT[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR).[S.l.]:[s.n.]，2013：2339-2346.
[4] LIN C C，PANKANTI S U，RAMAMURTHY K N，et al.Adaptive As-natural-as-possible Image Stitching[C]//IEEE Conference on Computer Visionand Pattern Recognition(CVPR).[S.l.]:[s.n.]，2015:1155-1163.
[5] ZHANG F，LIU F.Parallax-tolerant Image Stitching[C]//IEEE Conference on Computer Visionand Pattern Recognition (CVPR).[S.l.]:[s.n.]，2014:3262-3269.
[6] 何川，周军.具有直线结构保护的网格化图像拼接[J].中国图象图形学报，2018，23(07):973-983.
[7] CHEN Y S，CHUANG Y Y.Natural Image Stitchingwith the Global Similarity Prior[C]//European Conference on Computer Vision.[S.l.]:[s.n.]，2016:186-201.
[8] LIN K，JIANG N，CHEONG L，et al.SEAGU-LL:Seam-guided Local Alignment for Parallax-tolerant Image Stitching[C]//Computer Visio-ECCV 2016-14th European Conference.[S.l.]:[s.n.]，2016:370-385.
[9] CHUM O，MATAS M.Optimal Randomized RANSAC[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2008:1472-1482.
[10] KWATA V.Graphcut Textures：Image and Video Synthesis Using Graph[J].Acm Transactions on Graphics，2003，22(3):277-286.
[11] LI J，WANG Z M，LAI S M，et al.Parallax-tolerant Image Stitching Based on Robust Elastic Warping[J].IEEE Transactions on Multimedia，2018:1672-1687.
[12] ASEEM AGARWALA，MIRA DONTCHEVA，MANEESH AGRAWALA，et al.Interactive Digital Photomontage[J].ACM Transactions on Graphics，2004，23(3):294-302.
[13] ZHANG Jianming，SCLAROFF S，LIN Zhe，et al.Minimum Barrier Salient Object Detection at 80 FPS[C]//IEEE International Conference on Computer Vision.[S.l.]:[s.n.]，2015:1404-1412.
[14] BOYKOV Y，VEKSLER O，ZABIH R.Fast Approximate Energy Minimization via Graph Cuts[J].IEEE Transactions on Pattern Analysis & Machine Intelligence，2001，23(11):1222-1239.
[15] ANISH MITTAL，RAJIV SOUNDARARAJAN，ALANC BOVIK，Making a 'Completely Blind' Image QualityAnalyzer[J].IEEE Signal Processing Letters，2013，20(3):209-212.
Parallax Image Stitching Based on Feature Optimization and Optimal Stitching Seam
Citation format:SUN Shangwen， LIU Yu， XU Zhaohong， et al.Parallax Image Stitching Based on Feature Optimization and Optimal Stitching Seam[J].Journal of Ordnance Equipment Engineering,2021,42(06):207-212.