【机械制造与检测技术】
基于MED-SK算法的行星变速箱故障特征提取
某型坦克行星变速箱长期处于高温重载的工作环境下，负载常在大范围瞬时波动，齿轮故障难以及时发现并有效处理[1]，且变速箱包含3级行星传动，结构复杂，工作时噪声污染严重，故障特征提取工作较为困难。
变速箱在运转过程中，其运行状态主要表现为齿轮啮合振动、轴的扭振、噪声、润滑油温度、油液中的磨粒杂质等，以上几种表现都可以反映变速箱的运行状态，但对于齿根裂纹这类轻微故障而言，故障的动态响应特征较弱，变速箱的故障状态难以判别。且前期针对简单行星排齿轮故障的研究较多，对复合行星排齿轮故障研究较少，复杂的工作条件下使提取故障特征的信号处理工作难度提升。因此，针对行星变速箱的复合排微弱齿轮故障的特征提取研究工作具有重要意义。
当前，国内外学者针对简单行星排变速箱和多级行星变速箱的故障诊断开展了大量研究[2-3]，取得了一系列成果。然而，其对等比例缩小模型研究较多，对实际装备研究较少；对齿轮疲劳断裂、疲劳剥落等显性故障研究较多，对裂纹类微弱故障研究较少。
采用一定的信号处理方法提取振动信号中隐含的故障特征，是行星传动系统进行故障诊断的主要方式，如用局部线性嵌入算法提取故障特征[4]、小波相关排列熵提取故障特征[5]、希尔伯特-黄变换、变分模态分解[6]等现代信号处理方法，但是这些方法不能很好地应用于裂纹类微弱故障。
最小熵解卷积(MED)由Wiggins首次提出[7]，其本质是采用时域盲解卷积方法提高信号的信噪比，适用于齿轮和轴承的裂纹、磨损、点蚀等早期故障这类具有周期性脉冲冲击的振动信号，该方法已在轴承和齿轮轻微故障诊断领域得到了应用[8-9]。这种方法的基本思路是通过找到某个反向滤波器的最优参数最大化信号峭度值，从而反映信号的冲击特性。信号的峭度越大则熵越小，因此该反向滤波器称为最小熵解卷积FIR滤波器。最小熵解卷积对信号中的冲击成分进行放大，有助于齿轮早期故障的诊断。
Antoni[10]于2006年结合峭度与频谱分析，提出了谱峭度指标(SK)，其既能反映冲击强弱，又能指示相应频率位置，可以有效提取信号中的瞬态冲击成分。
基于上述理论，本研究首先运用最小熵解卷积预处理故障振动信号，再通过谱峭度法对预处理后的信号确定最优频带和带通滤波参数，最后从高频信号中解调出低频故障信号，实现微弱故障特征的提取与识别。
1 算法原理
1.1 最小熵解卷积理论
一般的线性时不变系统的机械振动信号用时域卷积可表示为：
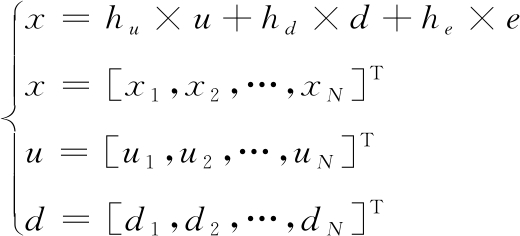
(2)
式中：x为离散加速度信号；u为其他未知输入信号；d为周期性故障冲击信号；e为噪声；N为信号长度；hu、hd、he分别为对应成分的时域卷积滤波系数。
通过L阶解卷积FIR滤波器f实现故障信号d的重构：
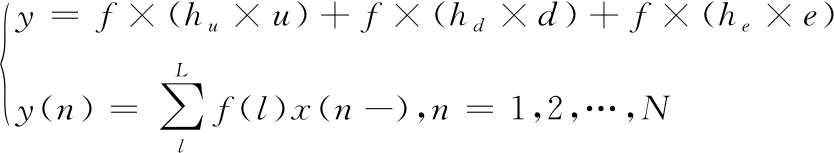
(2)
FIR滤波器f的阶数L满足L<N。为使输出信号y逼近周期性脉冲故障信号d，根据信号中各成分的峭度不同，选择一定的FIR滤波器使f×(he×e)和f×(hu×u)两项趋于零，消除信号中噪声e和未知信号成分u。以此设计可满足需求的f来提取信号中的脉冲故障信号。其采用归一化峭度作为目标函数，通过使目标函数最大化的方式得到最优结果，归一化峭度K(y)最大化过程如下：
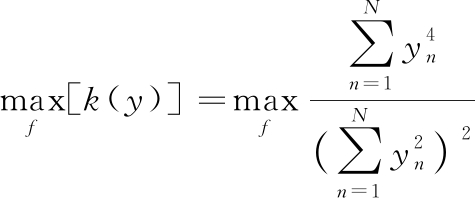
(3)
其中， f=[f1, f2, …, fL]T为求解解卷积FIR滤波器f的参数，可计算K(y)关于f的一阶偏导数并使其为零：
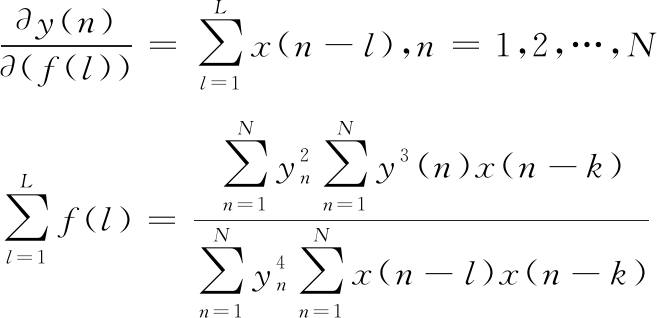
(4)
其矩阵形式为：
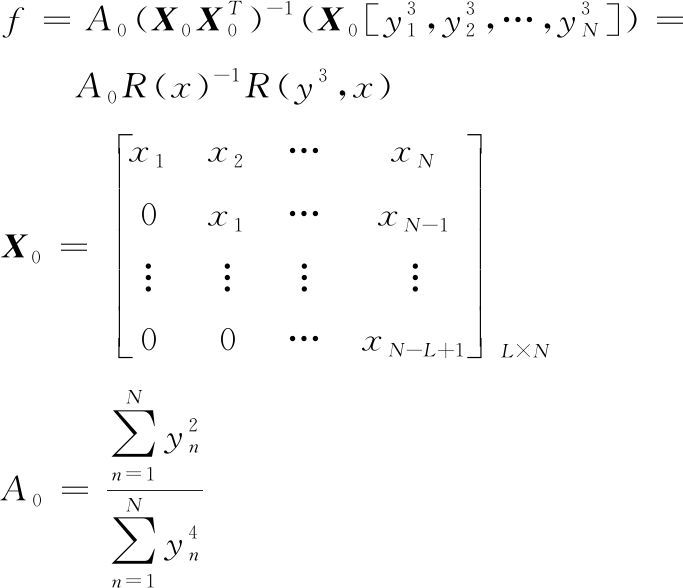
(5)
式中： R(x)-1为输入信号x的自相关Toeplitz矩阵；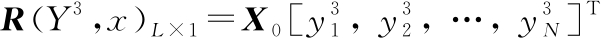
为输出信号y3与输入信号x的互相关矩阵。
综上所述，最小熵解卷积(MED)方法的主要过程是逐步迭代收敛，最终达到使信号峭度达到最大的目的，因此，最小熵解卷积(MED)算法实质上是求解最优解卷积滤波器f的问题。
1.2 谱峭度
谱峭度法的基本原理是计算信号每个频率的峭度，以发现隐含的不稳定频率边带。求解信号y(t)的谱峭度过程就是求解该信号的四阶频谱积累：
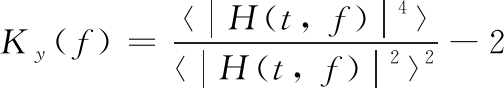
(6)
式中： H(t， f)为信号y(t)在频率f处的复合包络。
计算谱峭度有多种方法，如短时傅里叶变换(STFT)计算、小波变换计算以及快速峭度谱。快速峭度谱对瞬态冲击信号具有快速检测能力，且适用于信噪比高的行星变速箱振动信号[11]，因此本文通过该方法得到MED预处理后行星变速箱振动信号的快速峭度谱图，确定带通滤波参数并对信号进行滤波。
1.3 MED-SK算法
将最小熵解卷积的谱峭度法(MED-SK)应用于某型行星变速箱的信号处理方法，根据上述原理，首先利用最小熵解卷积对采集到的振动信号进行预处理，最大化信号中微弱的故障冲击成分，计算得到信号的峭度谱，选择最优的滤波器参数，然后利用带通滤波器对信号进行滤波，解调出信号中的低频成分，最终通过频谱分析找出信号中的故障频率成分实现信号的特征提取。算法步骤如图1所示。
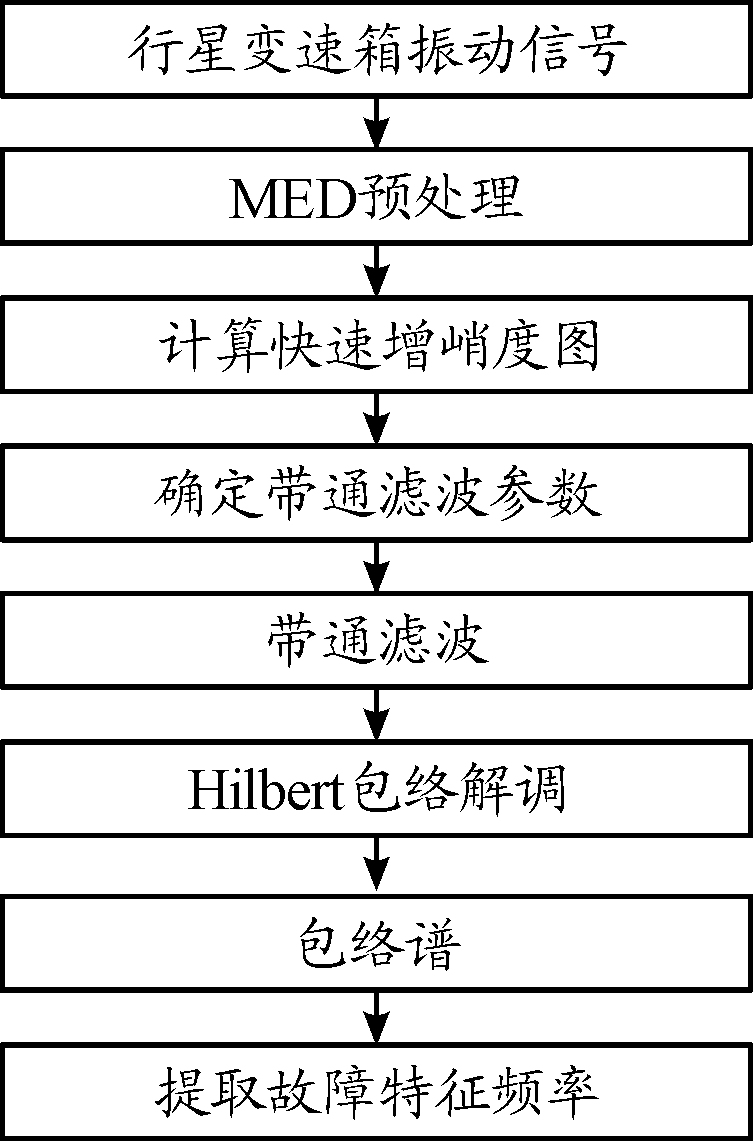
图1 MED-SK算法流程框图
2 试验方案设计
2.1 行星变速箱结构与工作原理
以某型坦克行星变速箱为对象搭建模拟试验台。试验台的动力源为三相电动机，额定功率为110 kW，可提供转频为0～25 Hz，利用换向传动箱将电动机动力垂直换向后传至离合器，离合器实现运转中换挡操作，变速箱两侧输出轴连接风冷式测功机模拟变速箱负载，可提供0～900 N·m范围内的稳定负载。
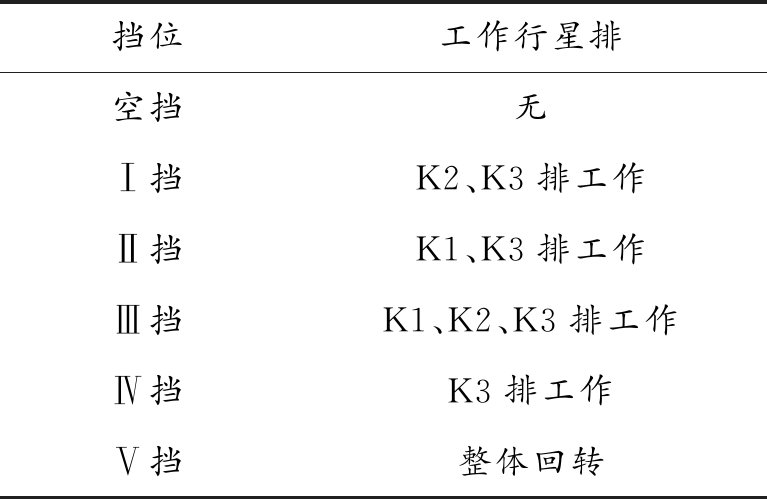
行星变速箱具有定轴传动部分和3排行星传动部分，3排行星传动部分中K1排为复合行星排，K2、K3排为简单行星排，图2为行星变速箱结构简图，表1为传动部分齿轮参数。变速箱通过控制各个行星排中的摩擦制动器约束不同部件的运动实现挡位变换，各挡位条件下行星排工作状况参照表2。
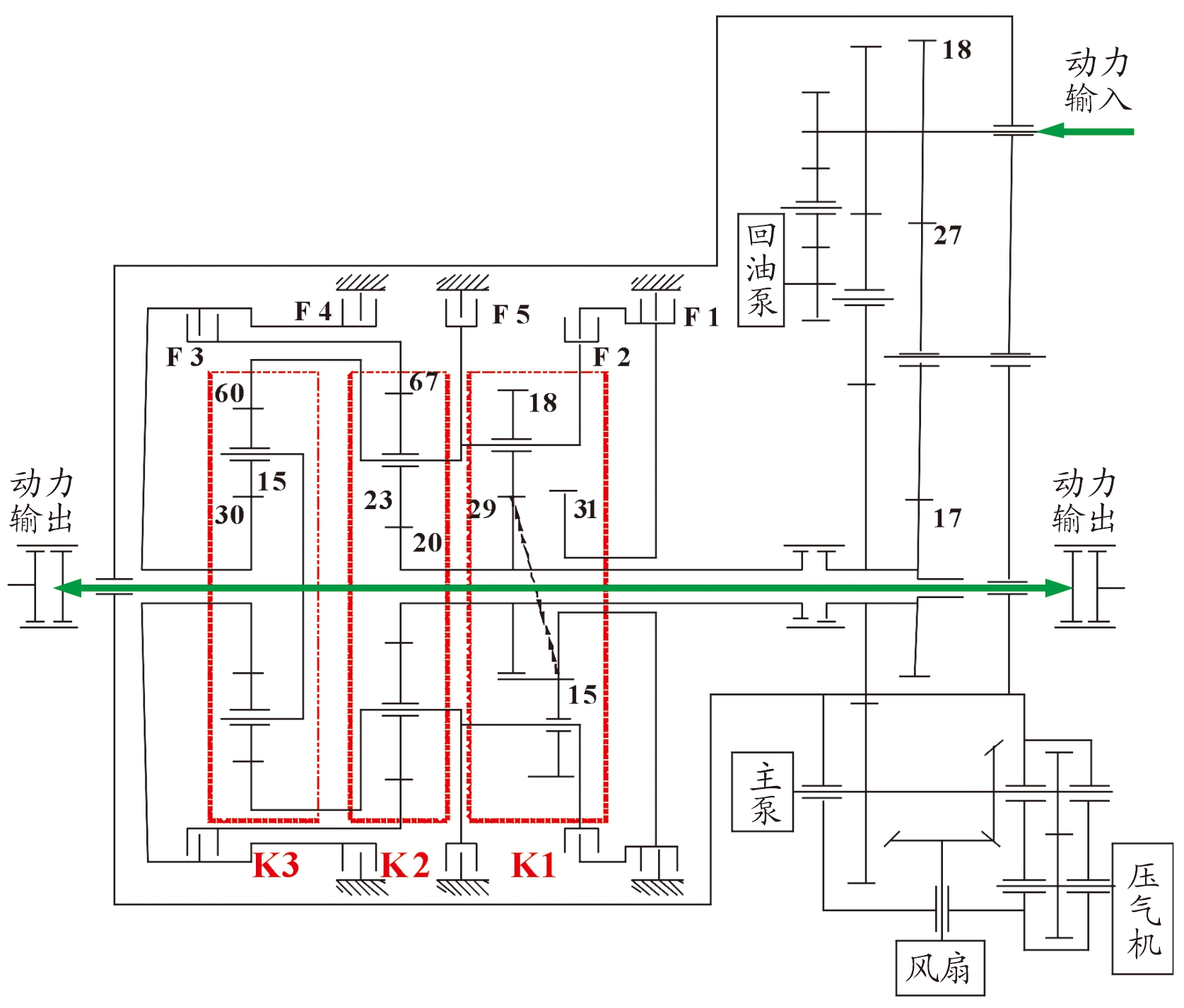
图2 行星变速箱结构简图
表1 行星变速箱传动部分齿轮参数
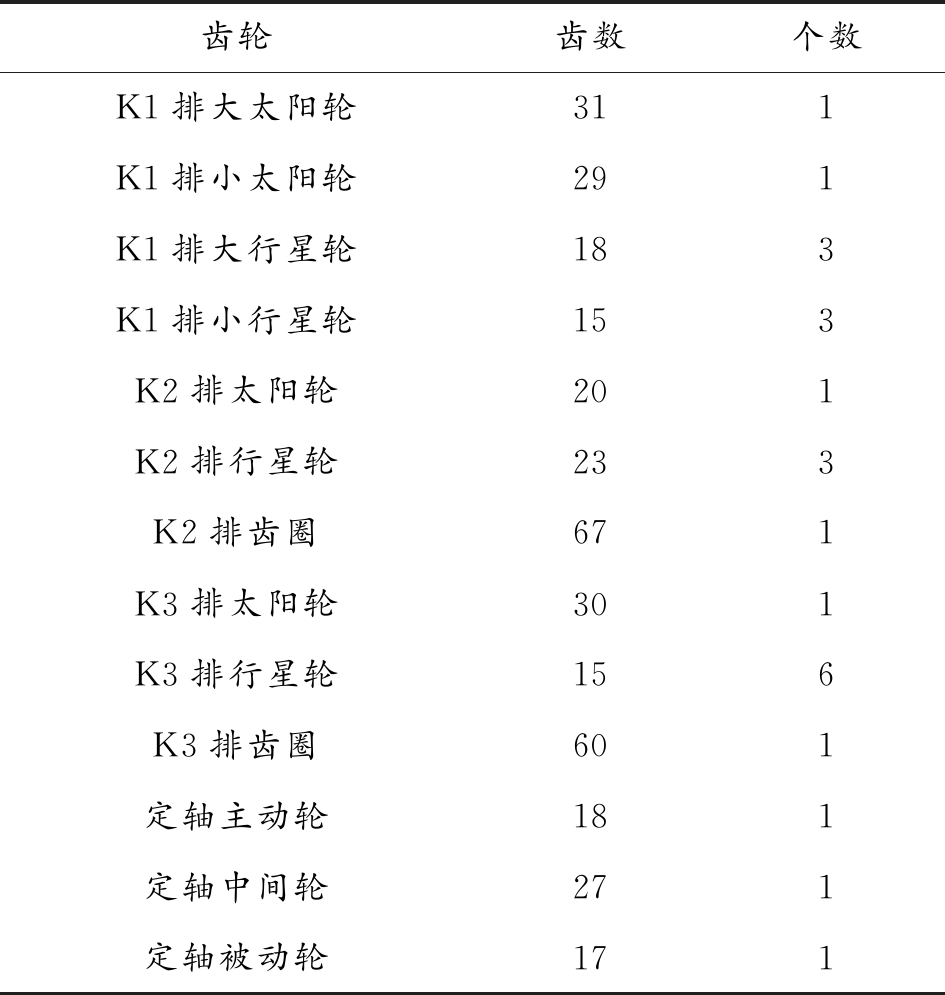
表2 各挡位行星排工作情况
2.2 故障注入与数据采集
变速箱的K1行星排是由齿数不同的2种太阳轮和2种行星轮构成的复合行星排，由于其结构复杂，发生故障时对其进行故障诊断具有较多难点。本次试验针对K1行星排的Z31太阳轮进行裂纹故障特征提取研究。将Z31太阳轮进行加工模拟裂纹故障件，通过变速箱的拆装换件来安装裂纹齿轮。故障件如图3所示。
图3 裂纹故障件图
根据表1，变速箱处于Ⅱ挡和Ⅲ挡工况时K1行星排都参与动力的传动，且Ⅲ挡时变速箱运行环境更为复杂。为验证MED-SK方法对复杂工况的可行性、对多种工况的适用性，分别采集变速箱Ⅱ挡和Ⅲ挡时的振动信号，试验数据分析处理以Ⅲ挡工况为主。设定输入转速600 r/min，采样频率20 kHz，每次数据采集时长30 s，振动传感器布置于箱体内部行星排框架上。
3 试验数据分析
在Ⅲ挡时，K1排、K2排、K3排都参与传动，工作状态较为复杂。实测振动信号的时域波形图和频谱分析结果图如图4。
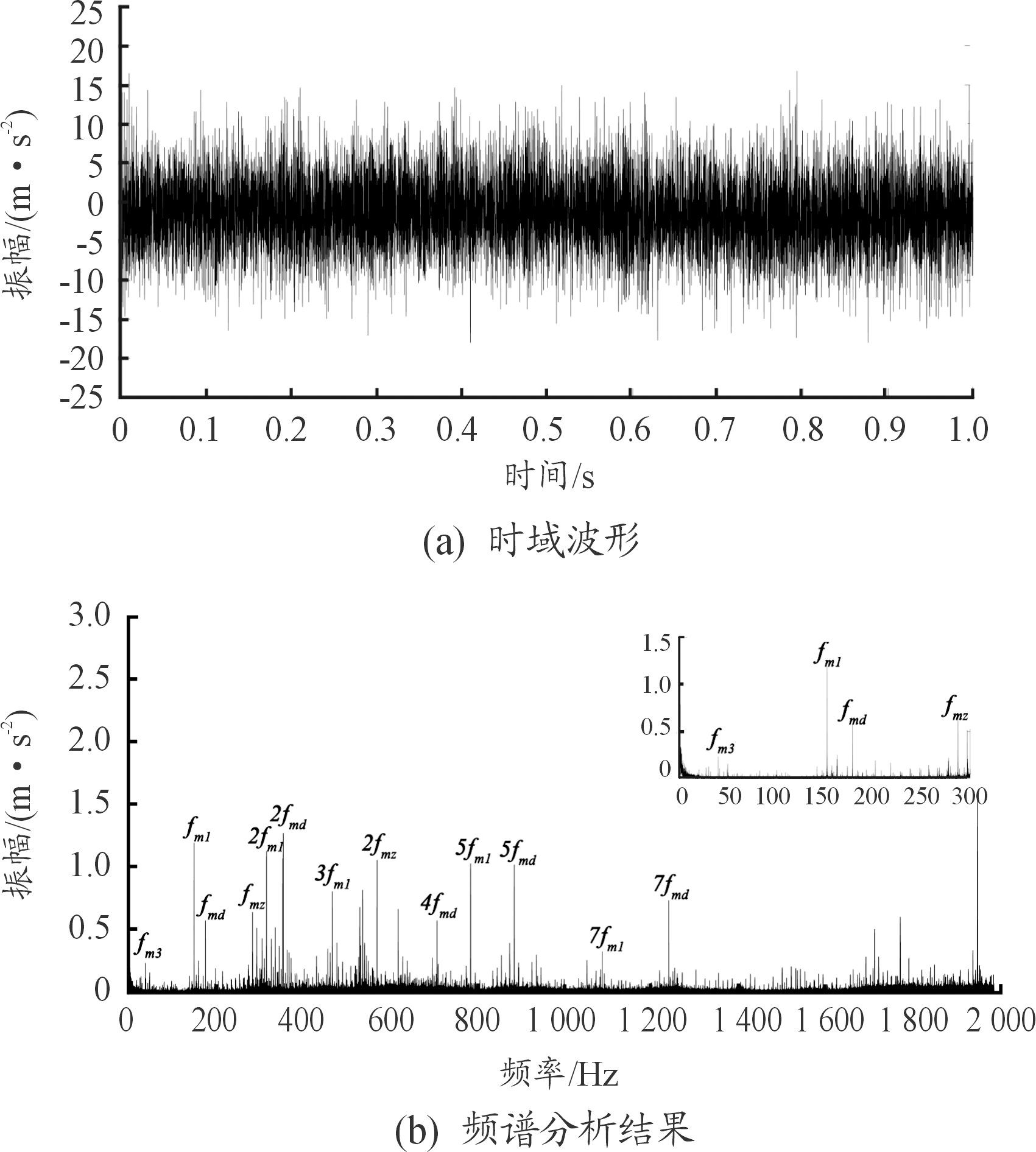
图4 实测振动信号时域波形图与频谱分析结果图
分析发现，Ⅲ挡时定轴传动部分实际啮合频率为178.4Hz，计算得出试验台电机实际输入转频为9.91 Hz，即试验台实际输入转速为594.6 r/min。图4(b)中各部分对应频率见表3所示。
表3 频谱分析结果中的典型特征频率
从图4(b)和表2可得到以下频率成分：定轴传动啮合频率fmd及其倍频，主泵啮合频率fmz，K1排啮合频率fm1及其倍频，K3排啮合频率fm3。回油泵啮合频率fmh、K2排啮合频率fm2未体现。低频部分的K1排Z31太阳轮裂纹故障频率被噪声淹没。
采用MED方法对原始振动信号进行预处理后的时域、频域波形图如图5所示。
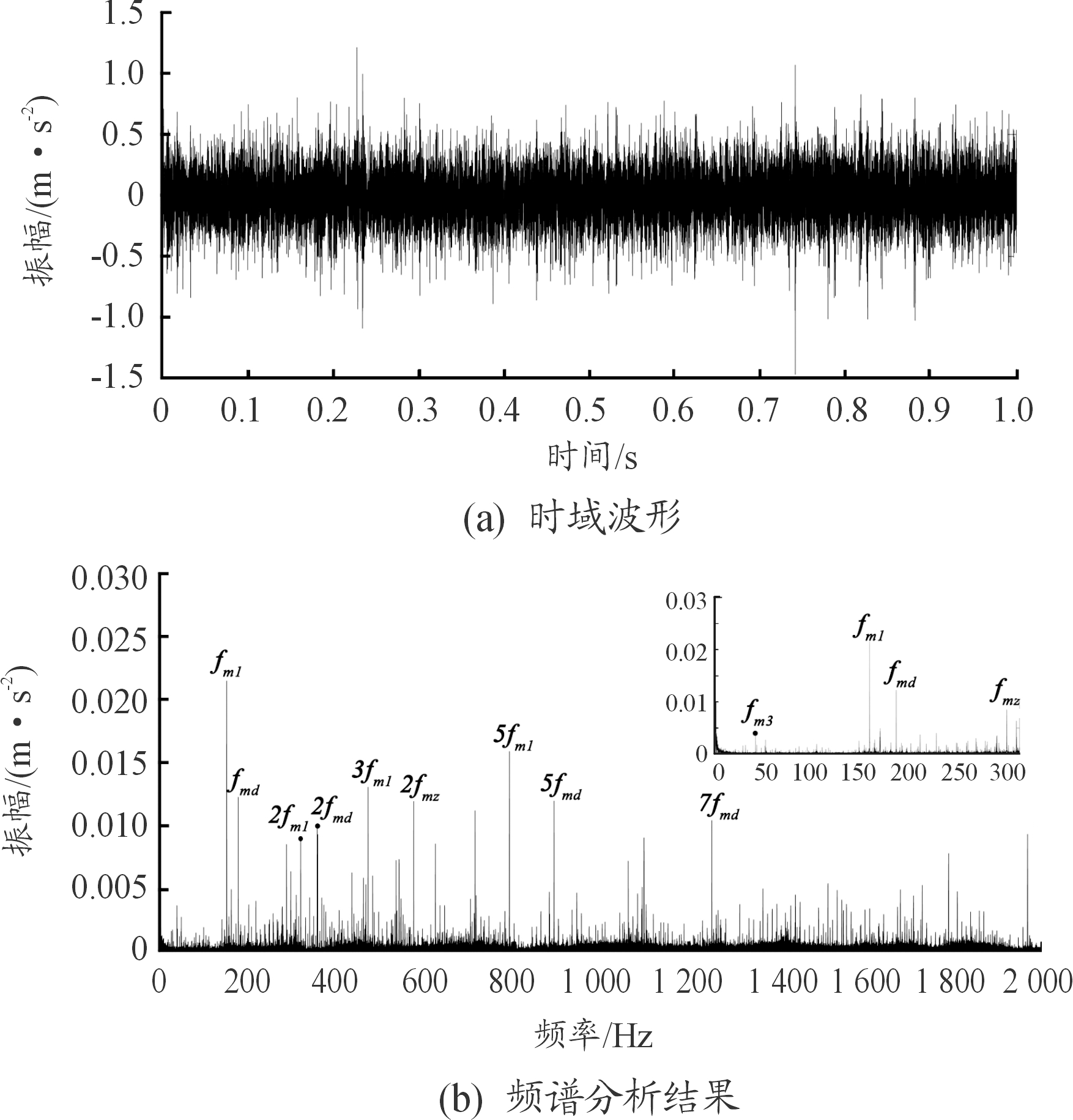
图5 MED预处理后时、频域波形图
从图5(a)可知，MED预处理后信号的噪声成分明显降低，信号冲击成分更加明显。对比图5(b)与图4(b)，MED预处理后频域波形图体现了更多频率成分，电机输入转频及其各次倍频在低频段出现但不够明显，K1排Z31太阳轮的故障特征频率未体现，需要对信号进一步处理。
对MED预处理后的振动信号与原始振动信号谱峭度图如图6所示。原始信号峭度值为2.27，MED处理后信号的峭度值提升到2.404，说明MED方法有效提升了原始信号的冲击成分。从图6(b)中峭度值最大的部分所在位置可确定待选滤波器的中心频率为8 418 Hz，带宽625 Hz，层数4.6。信号经滤波后，再进行包络谱分析可得到包络谱如图7，图7中各部分对应频率见表4所示。
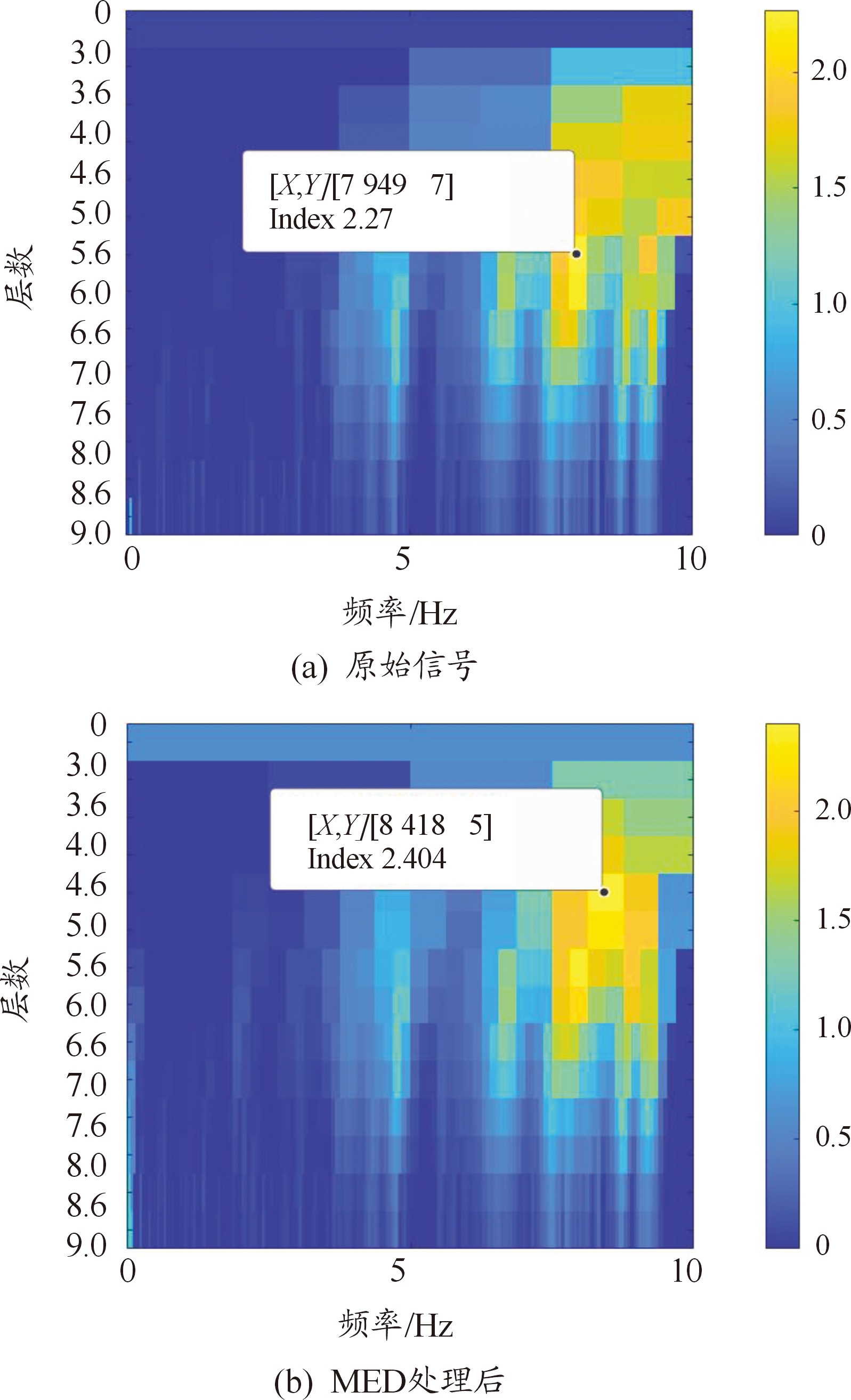
图6 谱峭度图
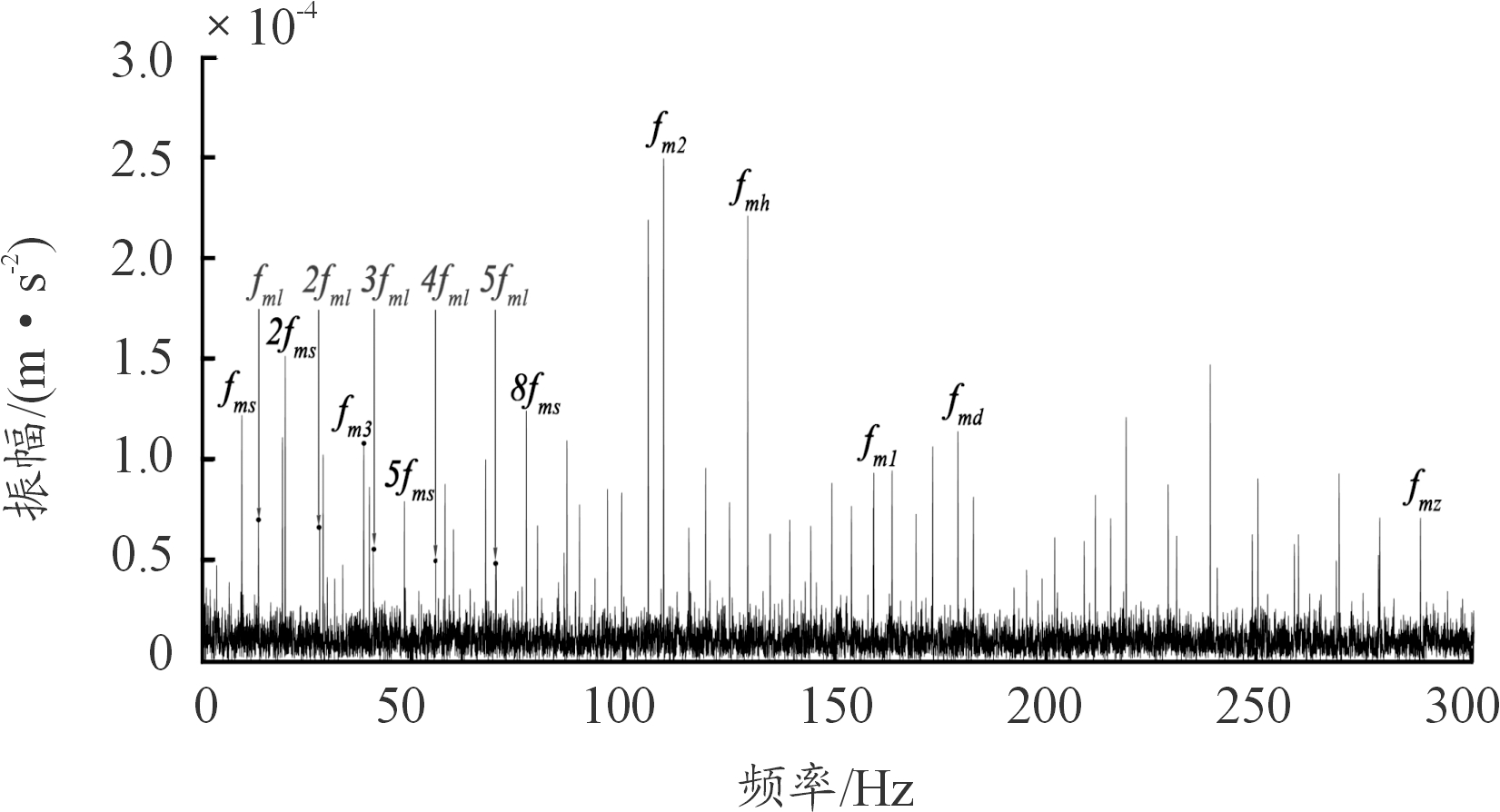
图7 MED-SK方法得到的包络谱
表4 MED-SK方法包络谱的典型特征频率
从图7可知，经MED-SK方法处理后的包络谱有效地提取出K1排Z31太阳轮裂纹故障特征频率fml及其倍频，电机输入转频fms及其倍频较为明显。同时，处理后的包络谱体现了各部分的啮合频率，图5(b)中未出现的回油泵啮合频率fmh、K2排啮合频率fm2也得到了较明显的体现。
图8给出了带通滤波后的时域波形，经过MED-SK方法处理后的时域波形的振动冲击得到了进一步增强。
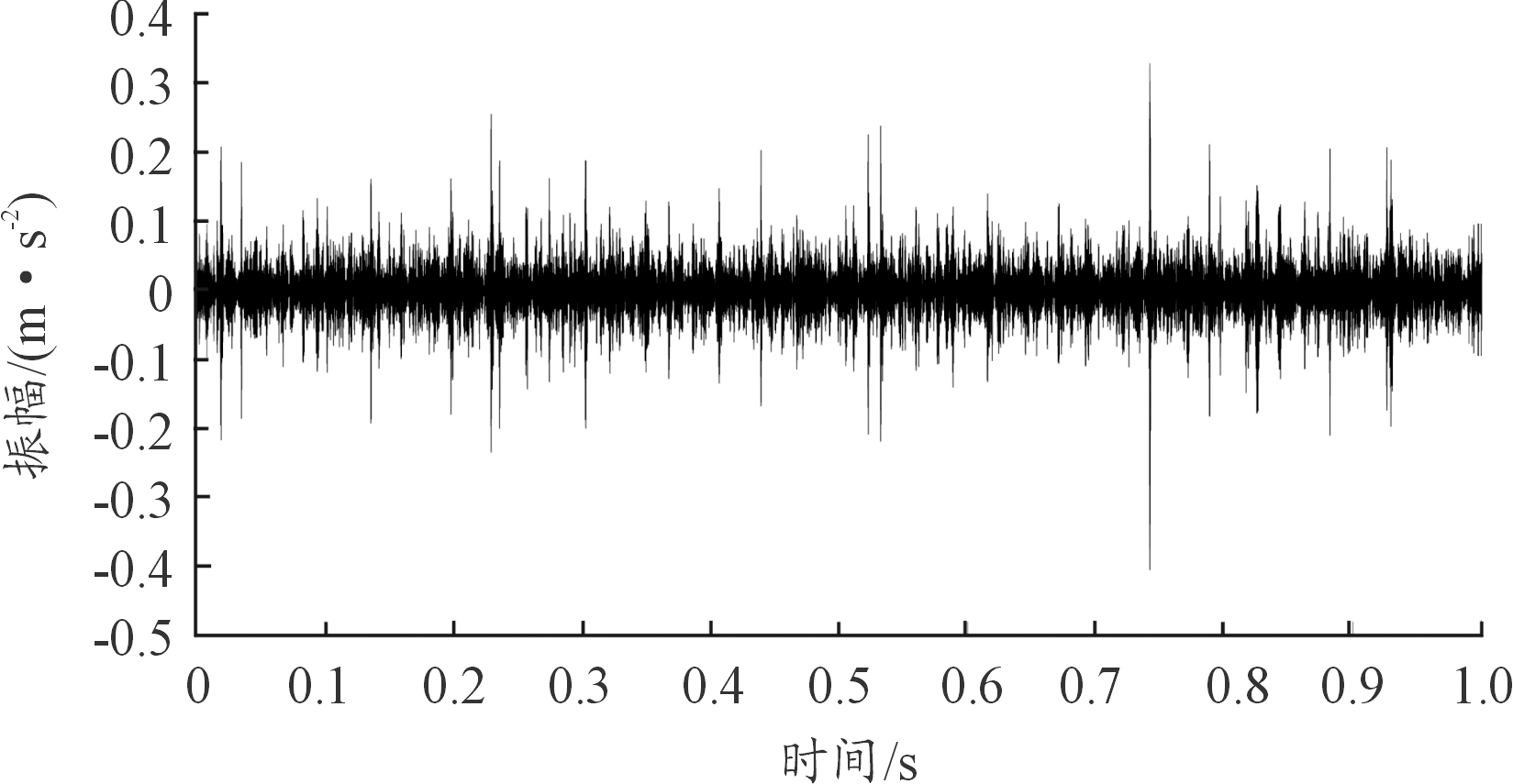
图8 MED-SK方法处理后的时域波形
同样通过MED-SK方法对Ⅱ挡工况下振动信号进行处理，此时只有K1排、K3排工作，频率成分较少。从图9(b)MED预处理后的频域波形图呈现出电机输入转频，体现了更多频率成分，再经过快速峭度谱图确定带通滤波参数、进行带通滤波后成功提取出K1排Z31太阳轮裂纹故障频率及其各次倍频，且较Ⅲ挡工况的包络谱更加清晰，表5对应图9中典型特征频率。
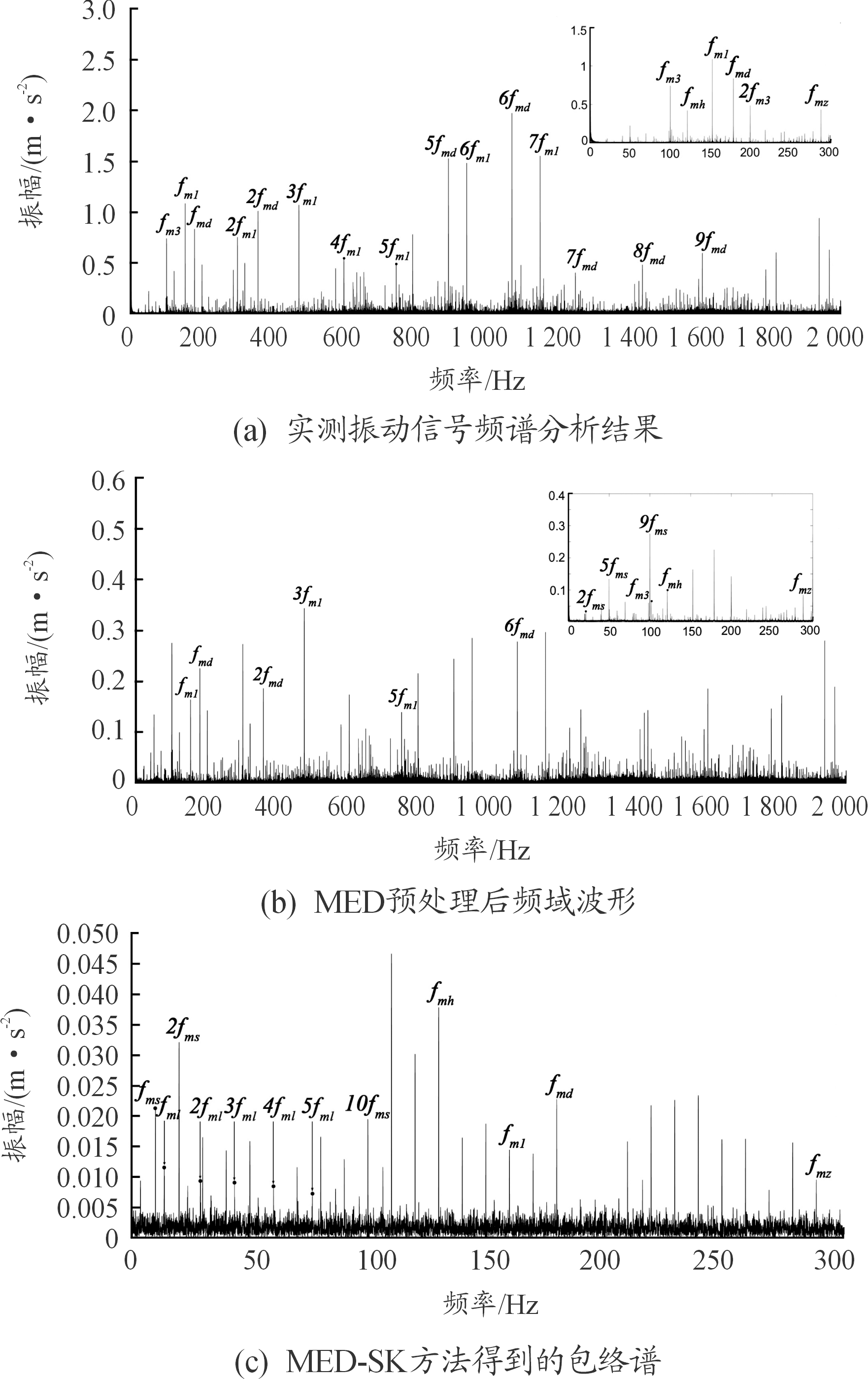
图9 MED-SK方法用于Ⅱ挡工况的故障特征提取
表5 Ⅱ挡工况的典型特征频率
综上所述，MED-SK方法能够在复杂工况、多种工况下有效提取复合行星排太阳齿轮裂纹故障特征。
4 结论
对台架试验获取的箱体表面实测振动信号进行频谱分析，发现振动信号受强噪声污染和信号传递衰减严重，难以体现变速箱主要振动频率成分及齿轮裂纹故障频率成分，需要能够抑制信号噪声，增强信号中冲击成分的信号处理、提取信号中的齿轮裂纹故障的冲击成分。针对该情况，本研究提出了基于最小熵解卷积的谱峭度算法(MED-SK)的基本原理及算法流程。
将信号进行MED-SK算法处理后，提升了信号的谱峭度，抑制了信号中的噪声干扰，使信号的振动冲击成分相比原信号更加明显，突出了齿根裂纹的故障频率，实现了行星变速箱振动信号中裂纹故障成分的识别，也证明了MED-SK算法能够增强信号中微弱的冲击成分，实现了齿轮裂纹等较为微弱的脉冲冲击类故障的诊断，对下一步复合行星排微弱故障研究具有指导意义。
[1] 冯辅周，安钢，刘建敏.军用车辆故障诊断学[M].北京：国防工业出版社，2007：1-42.
[2] 雷亚国，何正嘉，林京，等.行星齿轮箱故障诊断技术的研究进展[J].机械工程学报，2011，47(19):59-67.
[3] 孙灿飞，王友仁.直升机行星传动轮系故障诊断研究进展[J].航空学报，2017，38(7):106-119.
[4] 李波.基于流形学习的特征提取方法及其应用研究[D].合肥：中国科学技术大学，2008：20-21.
[5] 冯辅周，司爱威，饶国强，等.基于小波相关排列熵的轴承早期故障诊断技术[J].机械工程学报，2012，48(13):73-79.
[6] 杨大为，赵永东，冯辅周，等.基于参数优化变分模态分解和多尺度熵偏均值的行星变速箱故障特征提取[J].兵工学报，2018，39(09):1683-1691.
[7] WIGGINS R A.Minimum entropy deconvolution[J].Geo-exploration，1978，16:21-35.
[8] FENG Zhipeng，CHEN Xiaowang，LIANG Ming.Joint envelope and frequency order spectrum analysis based on iterative generalized demodulation for planetary gearbox fault diagnosis under nonstationary conditions[J].Mechanical Systems and Signal Processing，2016，56:242-264.
[9] 王宏超，陈进，董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报，2013，49(1):88-94.
[10] ANTONI J.The spectral kurtosis:a useful tool for characterising non-stationary signals[J].Mechanical Systems and Signal Processing，2006，20:282-307.
[11] 马新娜，杨绍普.典型快速谱峭图算法的研究及应用[J].振动与冲击，2016，35(15):109-114.
Fault Feature Extraction Method of Planetary Gearbox Based on MED-SK Algorithm
Citation format:WANG Zihan， CONG Hua， FENG Fuzhou, et al.Fault Feature Extraction Method of Planetary Gearbox Based on MED-SK Algorithm[J].Journal of Ordnance Equipment Engineering,2021,42(06):256-261.