基于自抗扰的冲压发动机导弹大过载机动控制
1 引言
冲压发动机在比冲方面比固体火箭发动机具有明显优势，导弹发射质量一定的情况下，采用冲压发动机比采用固体火箭发动机的射程显著增加，因此冲压发动机被视作下一代空空导弹、反舰导弹、反辐射导弹的首选动力装置。然而采用冲压发动机作为动力的导弹，其弹体、推进、姿态之间存在强耦合关系，此外地面试验获得的导弹气动特性和发动机推力特性也存在较大的不确定性，这使得冲压发动机导弹具有快时变、强非线性、强耦合、强不确定性、多约束等特点[1-4]。与超燃冲压动力高超声速飞行器不同，采用冲压动力的战术导弹在攻击目标时往往需要做大攻角机动飞行，这无疑使得其快时变、强非线性、强耦合、不确定性问题变得更为突出，为此设计能够有效抑制这种非线性、强耦合、不确定性影响的强鲁棒姿态控制系统就显得尤为必要。
自抗扰控制将控制系统设计时面临的未建模动态、内外部扰动等不确定性统一视为“总扰动”，并将其扩张为新的系统变量，采用扩张状态观测器对系统状态及总扰动进行估计，然后将总扰动估计引入控制器中对系统总扰动进行实时补偿，因而可以显著改善系统的鲁棒性能。与动态逆控制、滑模控制、自适应控制等[5-9]在高超声速飞行器姿态控制中得到了广泛应用并取得了良好效果的非线性方法不同，ADRC对被控对象模型精度要求较低，可以处理非线性、时变、强耦合等复杂不确定性系统，可以保证闭环系统良好的动态性能，同时具有结构简单、易于实现、不存在控制抖振等优点，因此在理论和工程实践中得到不断的发展和应用[10-16]。程明智等[12]针对高超声速飞行器模型参数不确定性问题，设计了滑模自抗扰控制器，获得良好的控制性能，但参数摄动对控制抖振有明显影响。方雪等[13]针对高超声速飞行器巡航飞行中存在的模型参数不确定和外界干扰的问题，采用线性扩张状态观测器对模型不确定项和外界干扰的精确估计和补偿，能够显著提升滑模控制器的扰动抑制能力和系统的鲁棒性。陈辰等[14]针对存在扰动、执行机构死区非线性以及系统不确定性的高超声速飞行器巡航飞行纵向控制问题，设计了非线性扰动观测器对系统复合扰动进行估计和补偿，有效降低了滑模控制器控制增益和抖振，并消除了执行机构死区特性对动态系统的影响。Sun等[15]针对飞行器俯仰通道大空域飞行控制问题，设计了基于增益调度的LADRC控制器，实现了对飞行器的高动态姿态控制。霍斯琦等[16]针对再入飞行器纵向控制问题，采用ESO对阻力加速度进行估计和补偿，所设计的控制器在环境不确定性和导航偏差干扰下仍具有良好的性能。
本文主要研究纵向平面内的大过载机动控制和马赫数控制问题。首先，对导弹纵向动力学模型精确线性化得到导弹过载和马赫数控制数学模型，然后分别设计了过载回路和速度回路的自抗扰控制器，并采用ESO对系统的总的不确定性进行实时估计和补偿，最后通过仿真对所设计的控制器的有效性进行验证。
2 冲压发动机导弹数学模型
2.1 纵向运动动力学方程
下面给出导弹纵向平面运动数学模型：
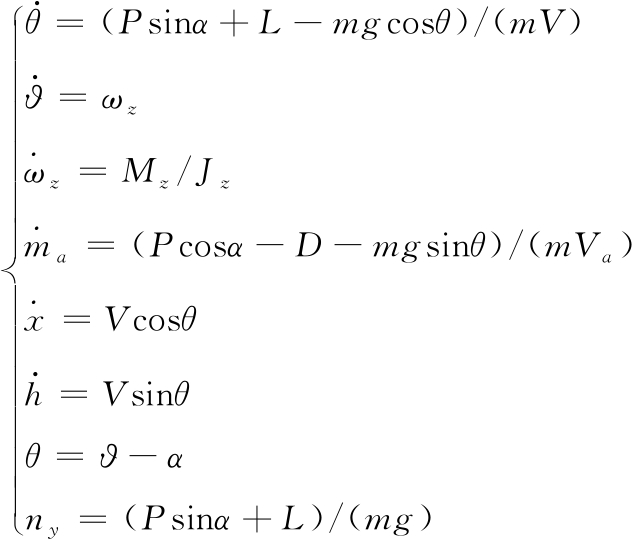
(1)
式中：m、V、α、θ、?、ma、h、ωz、g、Va分别为导弹质量、速度、攻角、弹道倾角、俯仰角、马赫数、飞行高度、俯仰角速度、重力加速度和音速，P、L、D、Mz、Jz分别为发动机推力、升力、阻力、俯仰力矩以及导弹沿着z轴的转动惯量，气动力和气动力矩的具体表达式为：
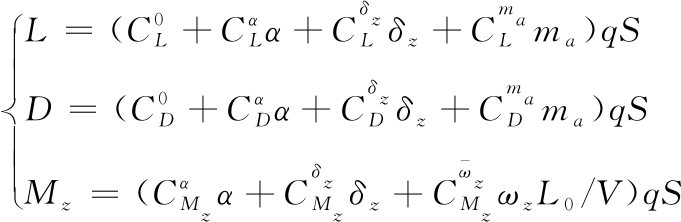
(2)
式中：q、S、L0分别为动压、参考面积、参考长度；δz为俯仰舵偏；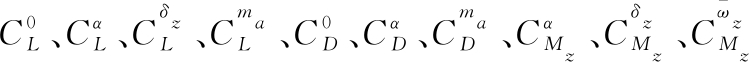
为气动系数。
本文采用冲压发动机为导弹全程主动机动飞行提供推力。冲压发动机推力是飞行高度、马赫数、攻角、燃油流量等变量的函数，具体可描述为[17-18]：
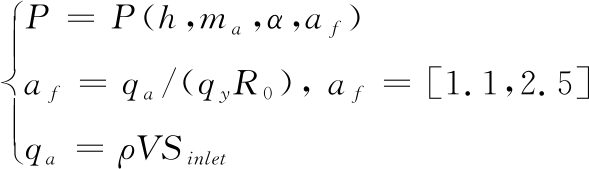
(3)
式中af、qa、qy、ρ、Sinlet分别为余气系数、空气流量、发动机燃油、大气密度和进气道捕获面积，R0为常数。
发动机推力可通过改变燃油流量来实现，燃油流量调节系统可描述为一个二阶系统：
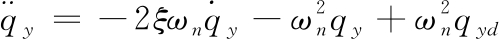
(4)
式中： ξ和ωn分别为二阶系统的阻尼和频率，分别取ξ=0.4，ωn=100，qyd为发动机供油流量调节器指令信号。
2.2 控制模型
式(1)～式(4)给出了冲压发动机导弹纵向运动数学模型，下面给出控制系统数学模型。定义X=[nyma]T，U=[δzqy]T，Y=[nyma]T。控制系统设计目标为希望准确光滑的跟踪期望输出Yd=[nyd mad]T。
为了开展控制器设计，需要对导弹纵向平面内动力学方程进行转换，由式(1)～式(3)可得：
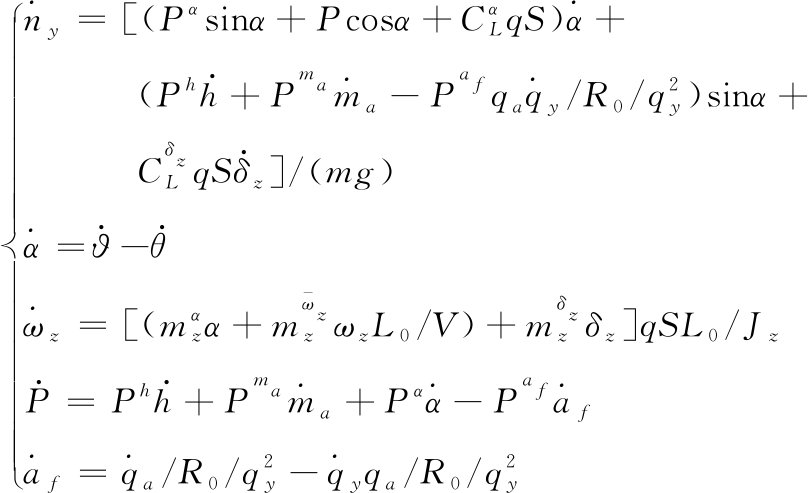
(5)
将上式记为：
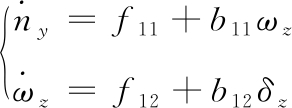(6)
式中：
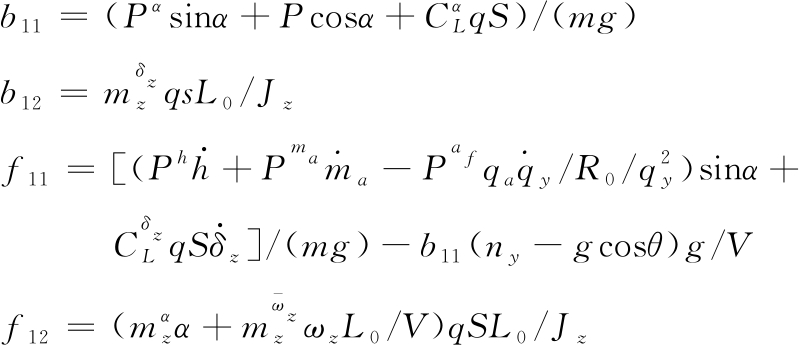
(7)
由于式(6)中过载ny与舵偏量δz不直接相关，因此对其进一步求导，得到：
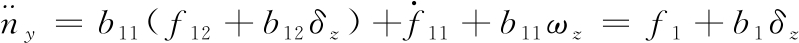
(8)
式中：
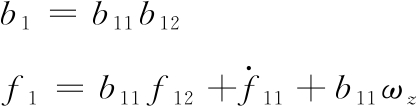
(9)
为了得到马赫数和燃油供油量的直接关系，对式(1)中第四式进行两次微分，并结合式(1)、式(4)、式(5)中第三式可得：
(10)
式中
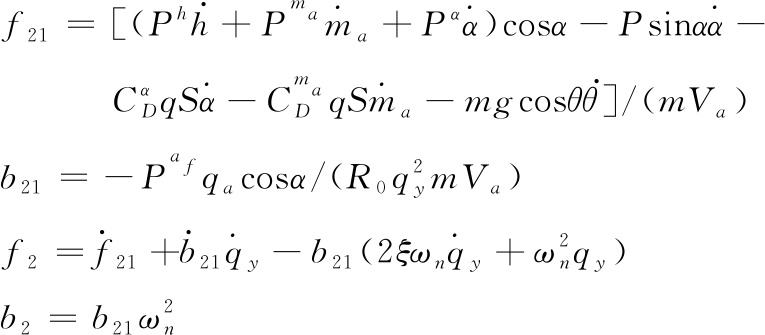
(11)
由式(8)和式(10)可得导弹过载和马赫数控制模型为：
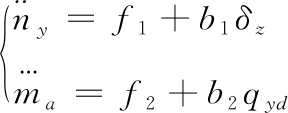
(12)
3 自抗扰控制器设计
3.1 过载回路跟踪控制器
过载回路设计目标是使得导弹过载能够快速准确跟踪过载指令nyd。定义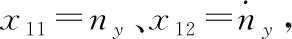
扩张状态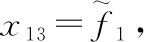
则由式(12)可得到如下扩张状态方程：
(13)
式中：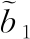
为b1的估计，
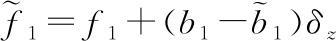为过载通道总扰动，包含系统已知模型部分、模型不确定性以及其他未建模部分，w1(t)为x13的微分，且w1(t)有界。
对式(13)可设计如下扩张状态观测器：
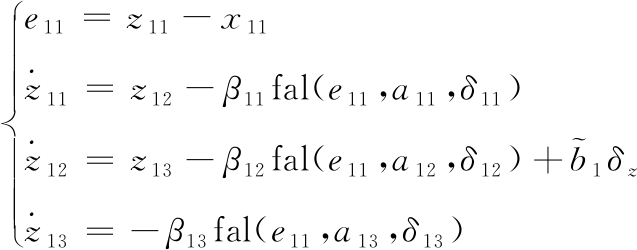
(14)
式中：z1i是x1i的估计，β1i是观测器增益，a1i、δ1i是非线性函数fal(e,a,δ)[8]的参数(i=1,2,3)。选择适当的参数β1i、a1i、δ1i可使得式(14)能够准确的估计式(13)的各状态量。
针对式(13)，取控制量δz为：
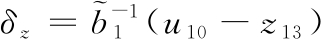
(15)
式中u10为虚控制量，将上式代入式(13)可得到如下积分串联型系统：
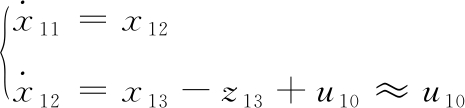
(16)
对上式可设计如下非线性状态误差反馈控制律：
u10=k11fal(e11,a14,δ14)+k12fal(e12,a15,δ15)
e11=υ11-z11
e12=υ12-z12
(17)
式中υ11、υ12为过载指令nyd及其微分，由于冲压发动机导弹过载与发动机推力存在强耦合关系，合理安排过载指令nyd的过渡过程有利于获得更好的控制性能。υ11、υ12的具体计算过程见文献[8]，k11、k12为可调参数，a1i、δ1i(i=4,5)定义与式(14)相同。
过载通道ADRC控制回路结构如图1所示。
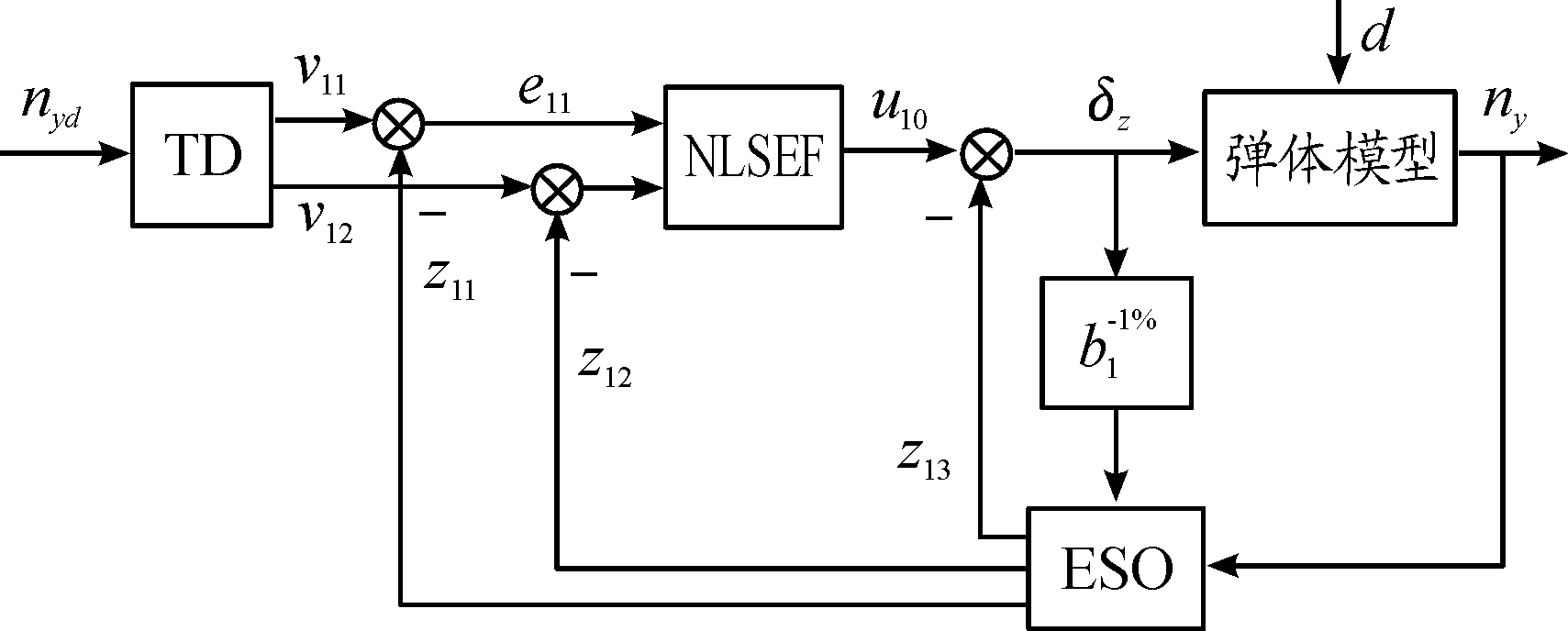图1 过载通道ADRC控制回路结构示意图
Fig.1 ADRC control diagram of overload loop
3.2 马赫数回路跟踪控制器
马赫数回路的设计目标是使得导弹过载能够快速准确的跟踪马赫数指令mad。定义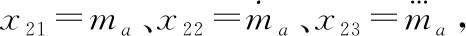
扩张状态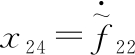
则由式(12)可得到如下扩张状态方程：
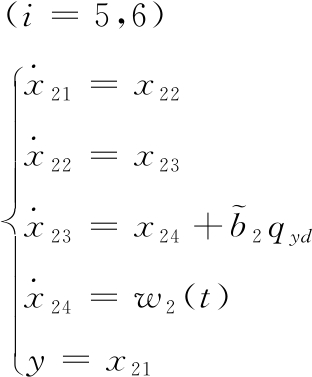
(18)
式中：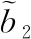
为b2的估计，
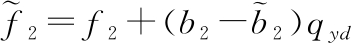为马赫数通道总扰动，包含系统已知模型部分、模型不确定性以及其他未建模部分，w2(t)为总扰动x24的微分，且w2(t)有界。
同样的对式(18)设计如下扩张状态观测器：
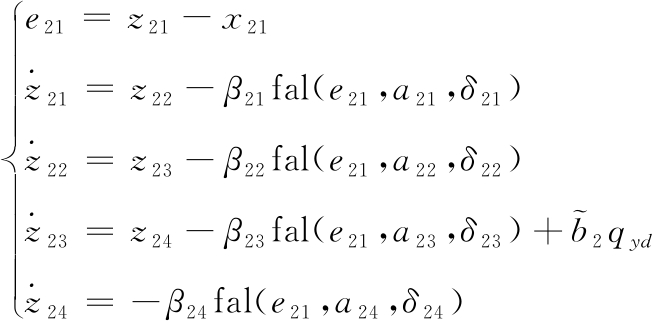
(19)
其中z2i是x2i的估计， β2i是观测器增益，a2i、 δ2i是非线性函数fal(e,a,δ)的参数(i=1,2,3,4)。
针对式(18)，取控制量qyd为：
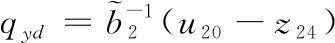
(20)
从而(18)可化为不包含任何未知参数的三阶积分串联型系统：
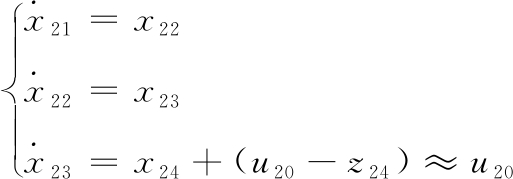
(21)
其中u20为待设计的虚控制量。根据自抗扰控制理论，可以设计如下非线性状态误差反馈控制律：
u20=k21fal(e21,a25,δ25)+k22fal(e22,a26,δ26)
e21=υ21-z21
e22=υ22-z22
(22)
式中υ21、υ22为马赫数指令mad及其微分。k21、k22、a2i、δ2i(i=5,6)的定义与式(17)相同。
马赫数通道ADRC控制回路结构如图2所示。
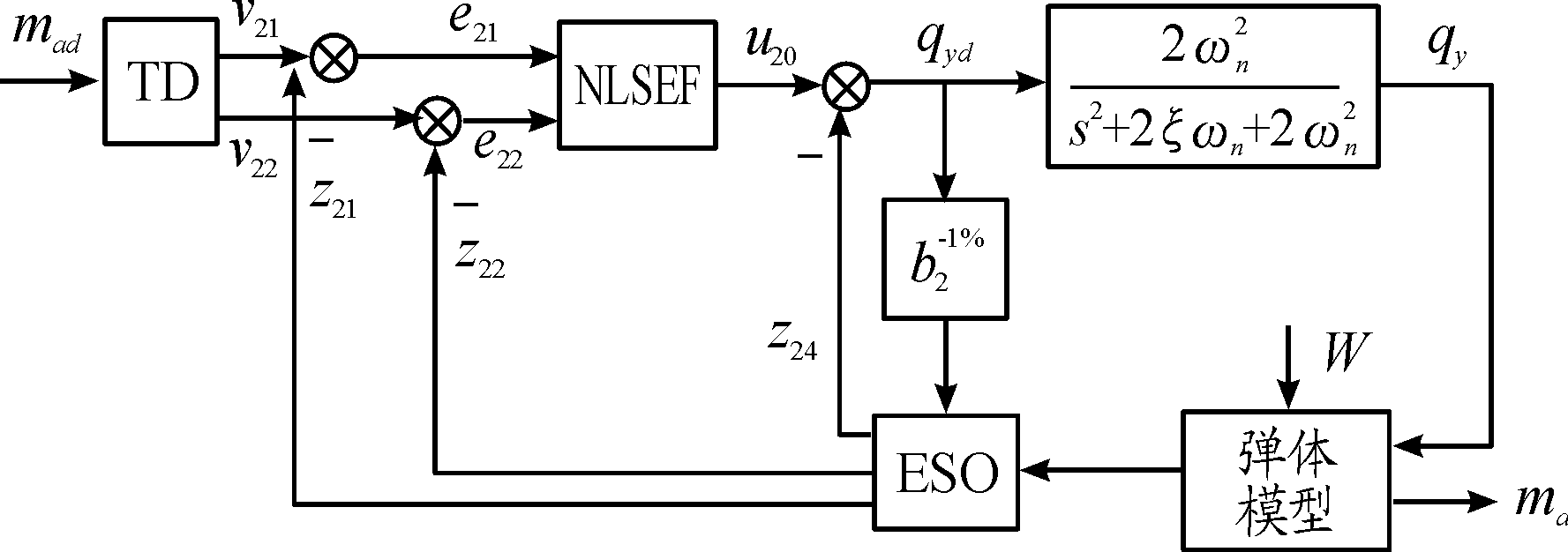
图2 马赫数通道ADRC控制回路结构示意图
Fig.2 ADRC control diagram of Mach loop
4 仿真分析
假定导弹飞行初始参数为：导弹质量m=900 kg，速度V=885 m/s，高度h=10 km，弹道倾角θ=0°，俯仰角和攻角 ?=α=1.3°，舵偏角δz=0，qy=1.1 kg。
控制器参数设置如下：
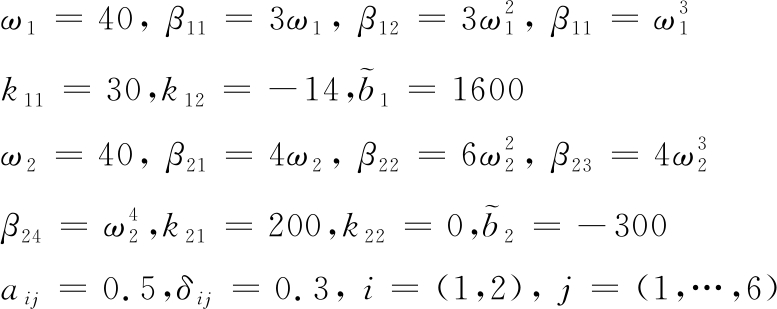
(23)
为了考察控制器性能，分别对马赫数通道和过载通道进行仿真试验。仿真1主要考察马赫数通道指令响应情况，控制指令设置如下：
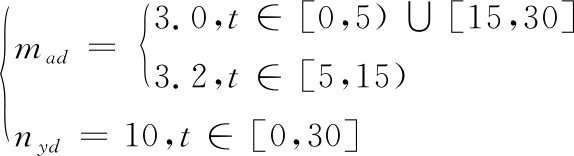
(24)
仿真1结果如图3～图5所示。
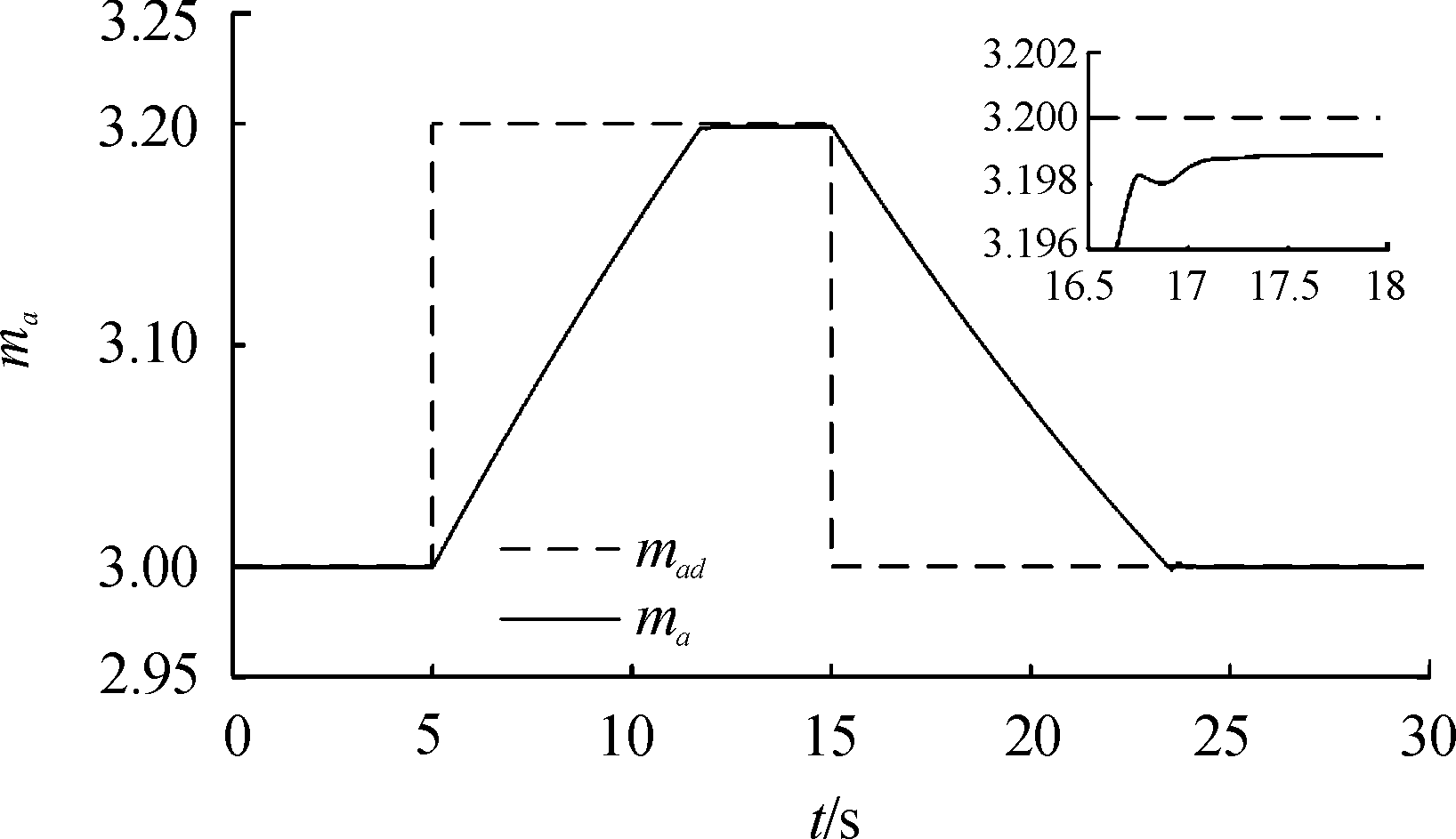
图3 马赫数指令及跟踪曲线
Fig.3 Reference and response of Mach control
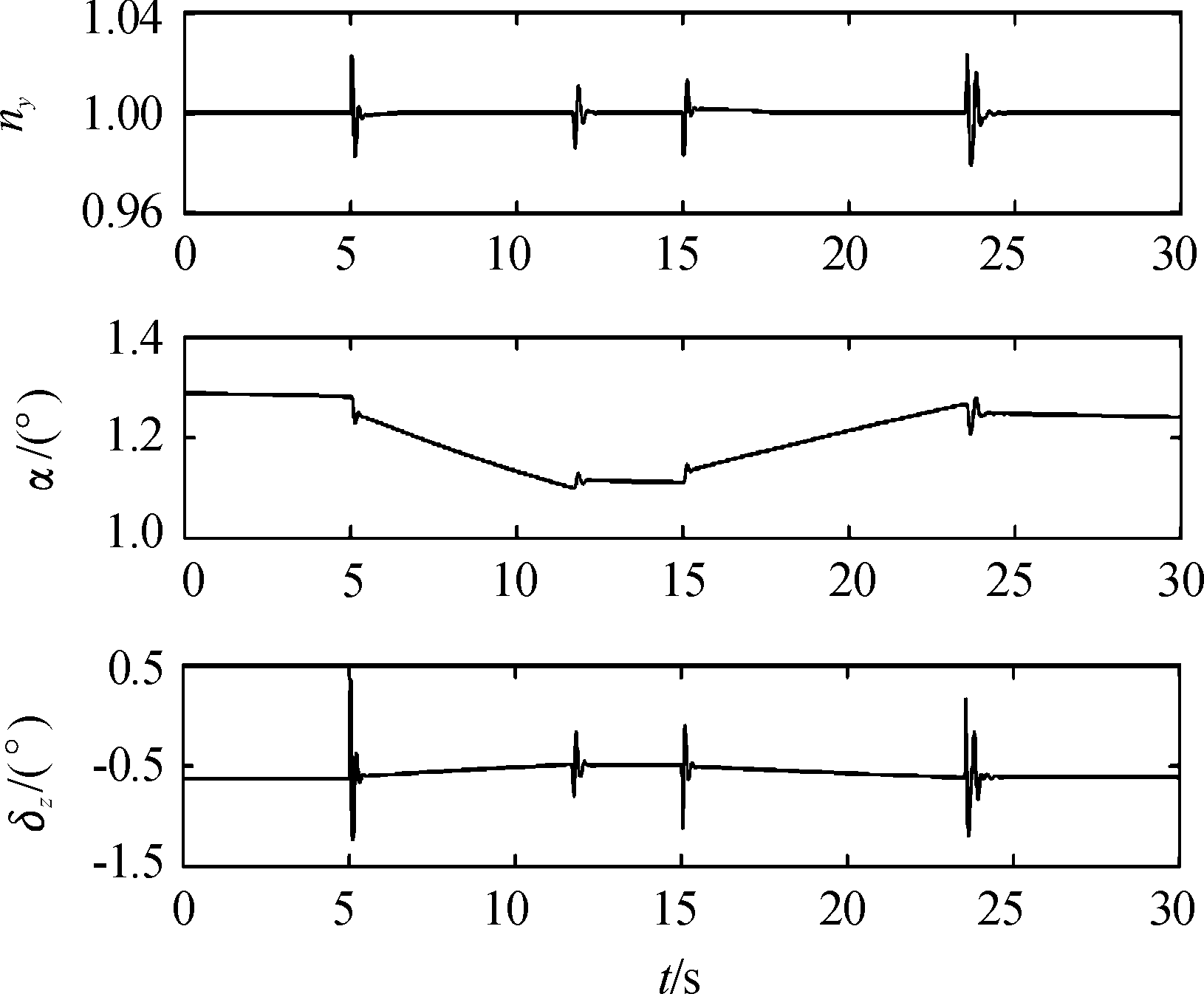
图4 过载、攻角、舵偏响应曲线
Fig.4 Response of overload，attack angle and rudder deflection angle
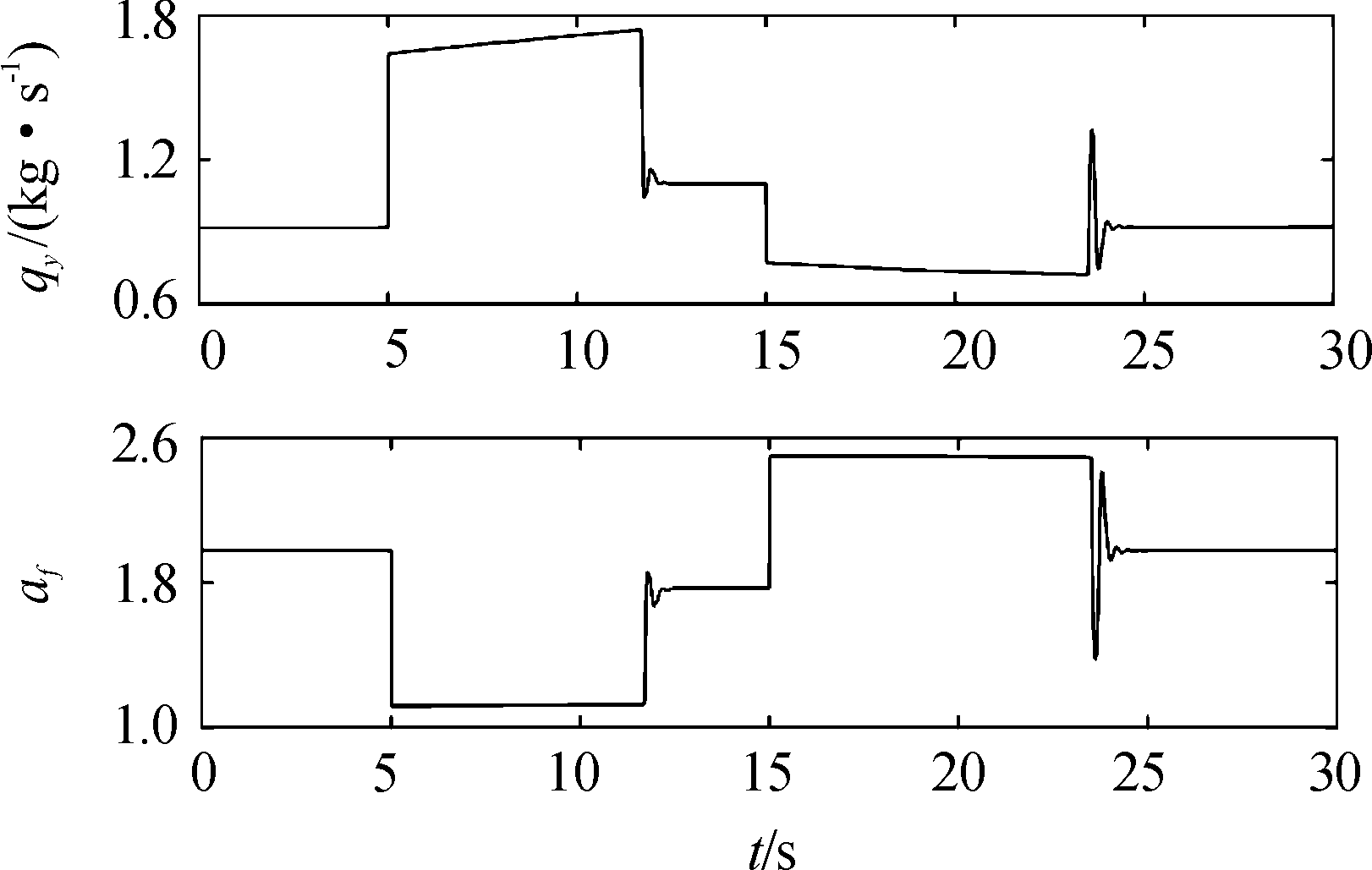
图5 供油量、余气系数响应曲线
Fig.5 Response of fuel flow and fuel-air ratio
从图3可以看出导弹马赫数能够很好的跟踪指令，没有超调量，稳态误差约为1%。马赫数由3.0上升到3.2的时间为11.6 s，这主要是冲压发动机推力裕量较小，在导弹加速过程中af一直处于最小值1.1，即发动机处于最大允许供油状态，这从图5可以看出。此外，从图4可以看出，在导弹加速和减速过程中，导弹过载ny和舵偏δz都仅在马赫数变化率较大的地方发生较大变化，其他时间幅值都较小，这表明所设计的控制器较好的实现了马赫数通道和过载通道的解耦。图4中攻角发生明显变化，这主要是导弹飞行速度变化后，导弹维持巡航飞行所需的配平攻角也发生相应变化。从图5可以看出，冲压发动机在导弹由Ma3.0加速至Ma3.2的过程中处于最大供油状态，在导弹马赫数由3.2减速至3.0的过程中处于最小供油状态。从图6中可以看到，导弹做加减速机动时，马赫数通道的扰动比较大，而过载通道的扰动比较小，这是因为机动过程中导弹攻角变化不大，主要是发动机燃油流量快速变化导致马赫数通达扰动较大。
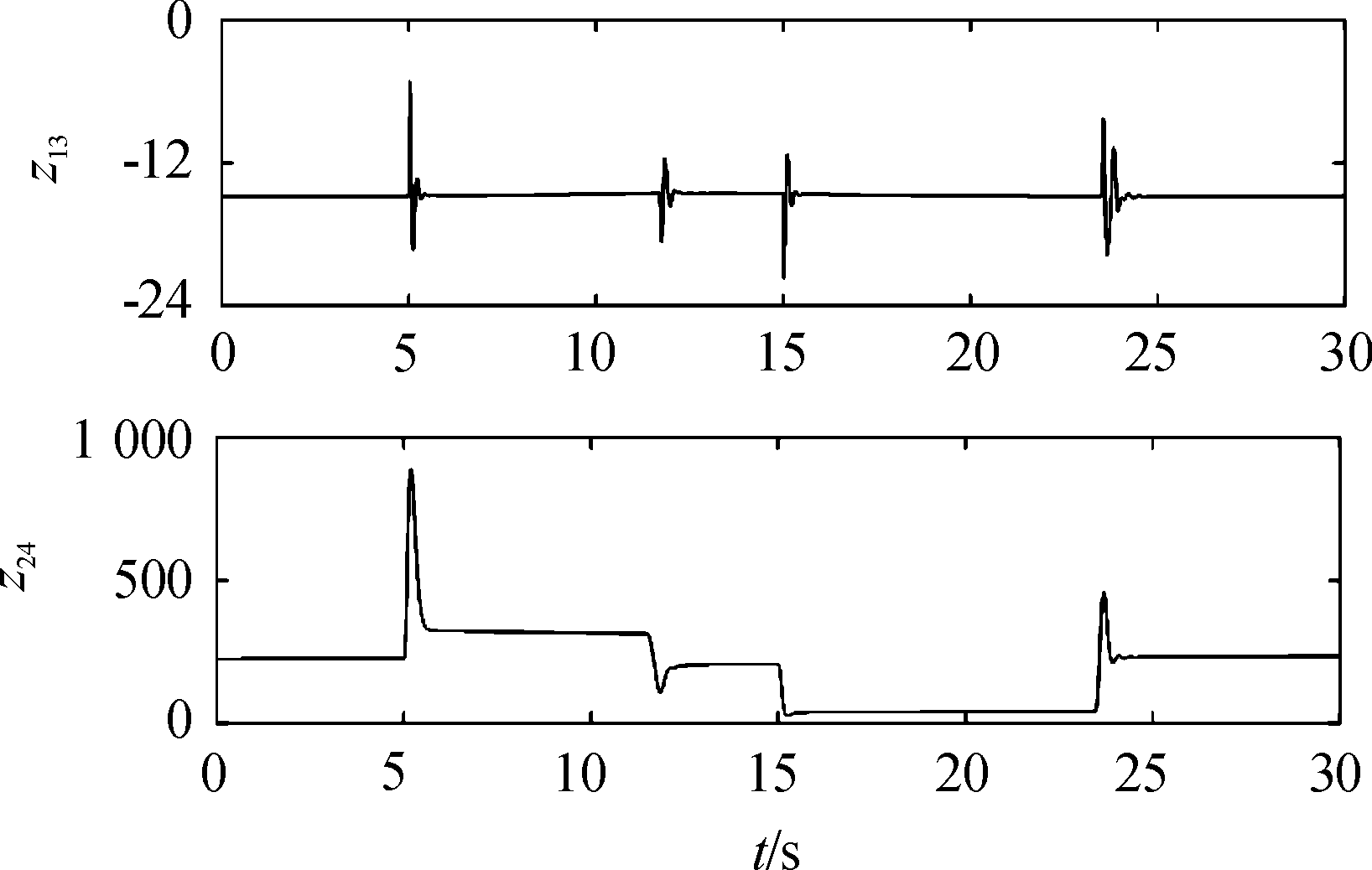
图6 过载通道和马赫数通道总扰动估计曲线
Fig.6 Estimation of overall disturbance of overload loop and Mach loop
仿真2主要考察过载通道指令响应情况，控制指令设置如下：
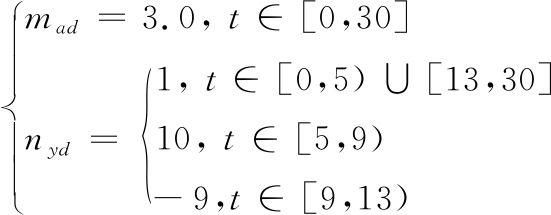
(25)
仿真结果如图7～图11所示。
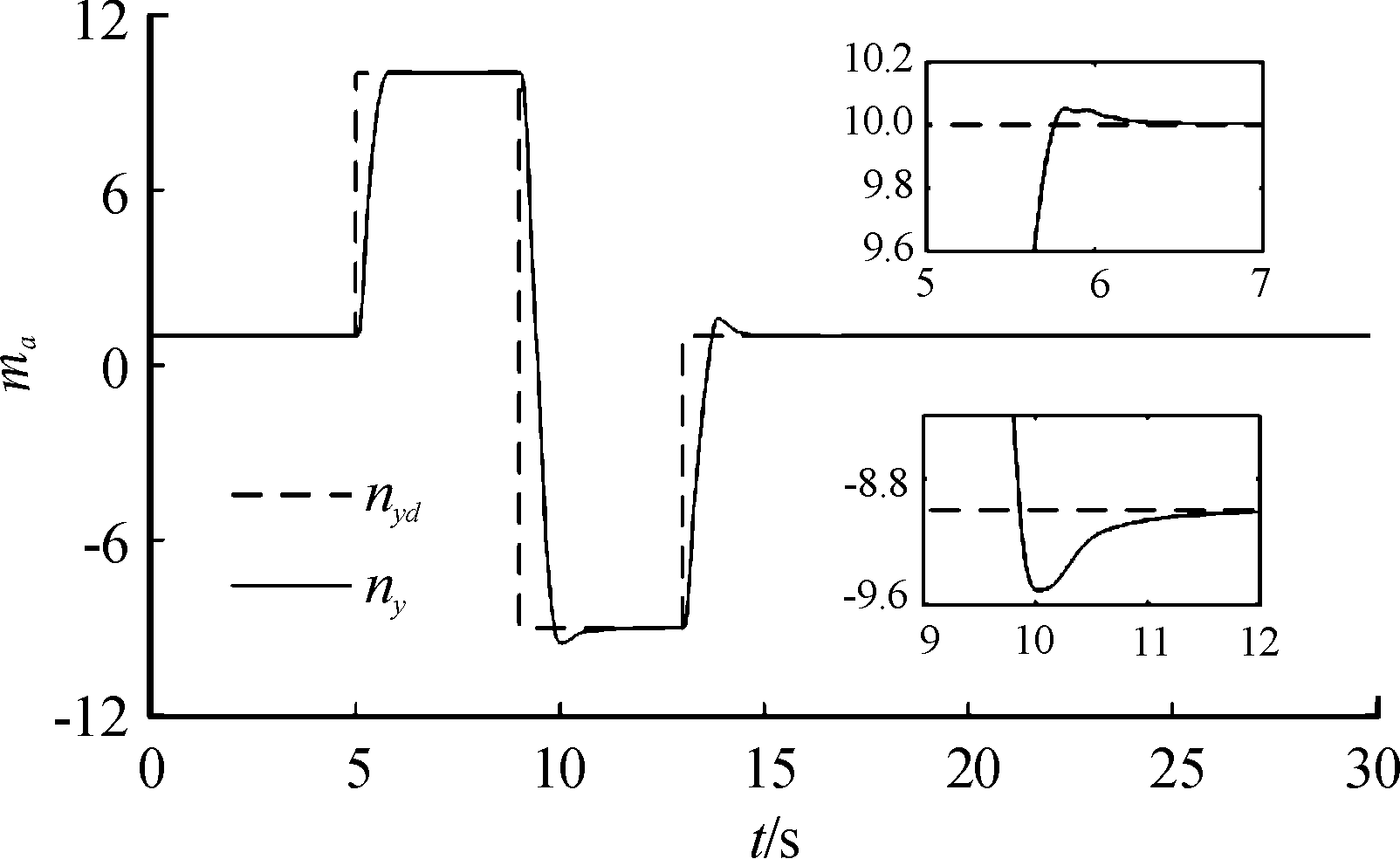
图7 过载指令及响应曲线
Fig.7 Reference and response of overload control
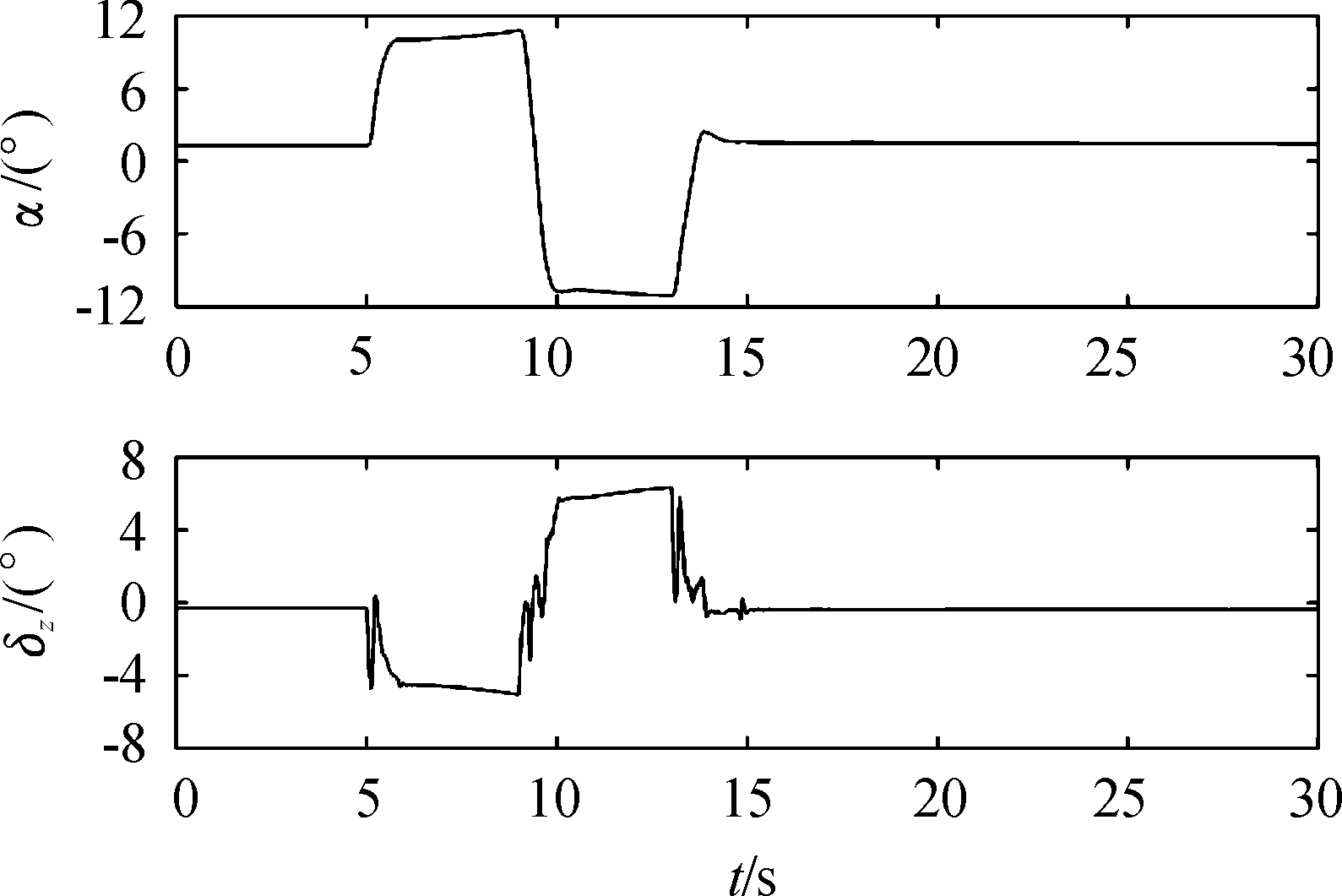
图8 攻角与舵偏响应曲线
Fig.8 Response attack angle and rudder deflection angle
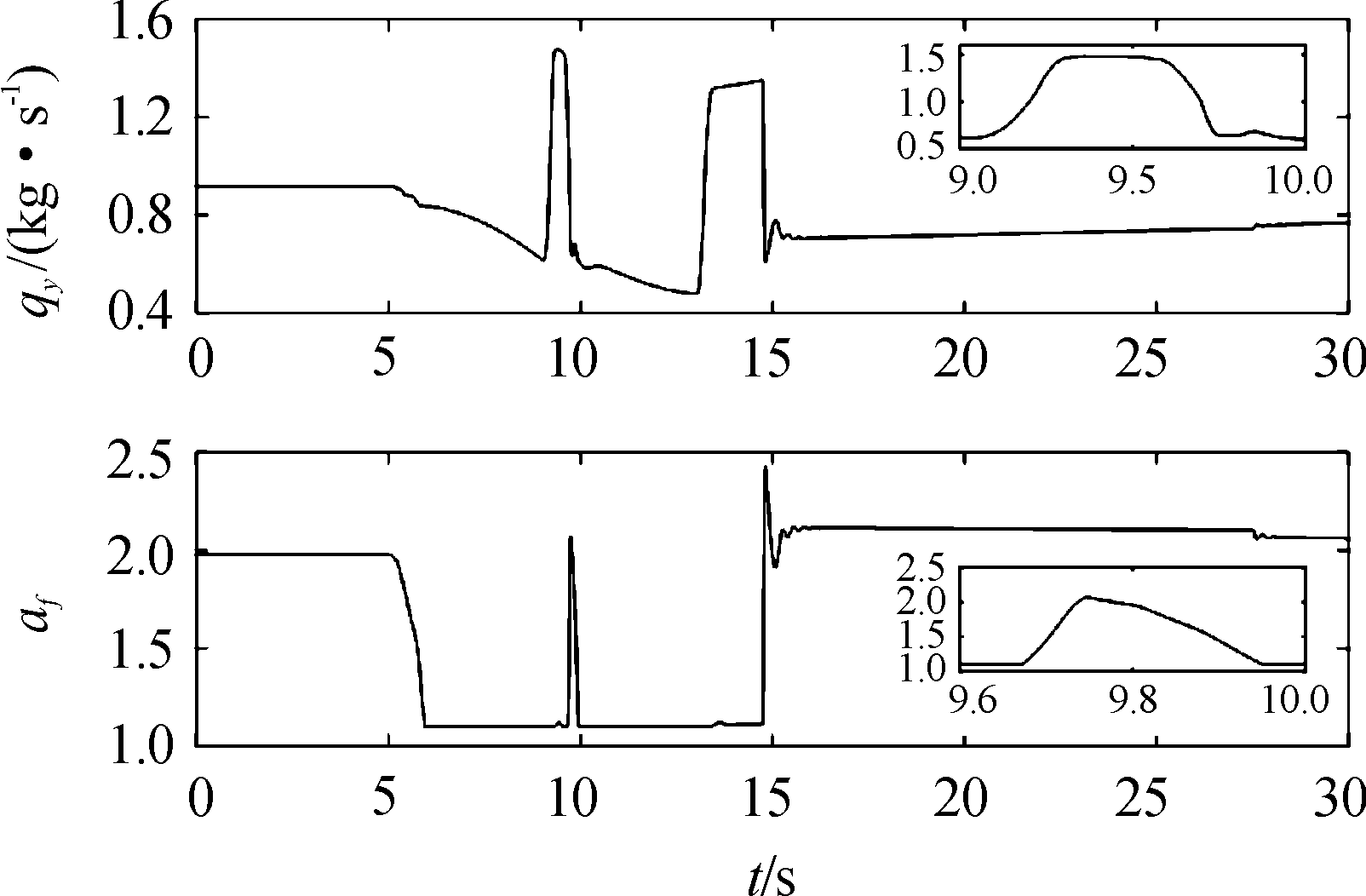
图9 燃油流量与余气系数响应曲线
Fig.9 Response of fuel flow and fuel-air ratio
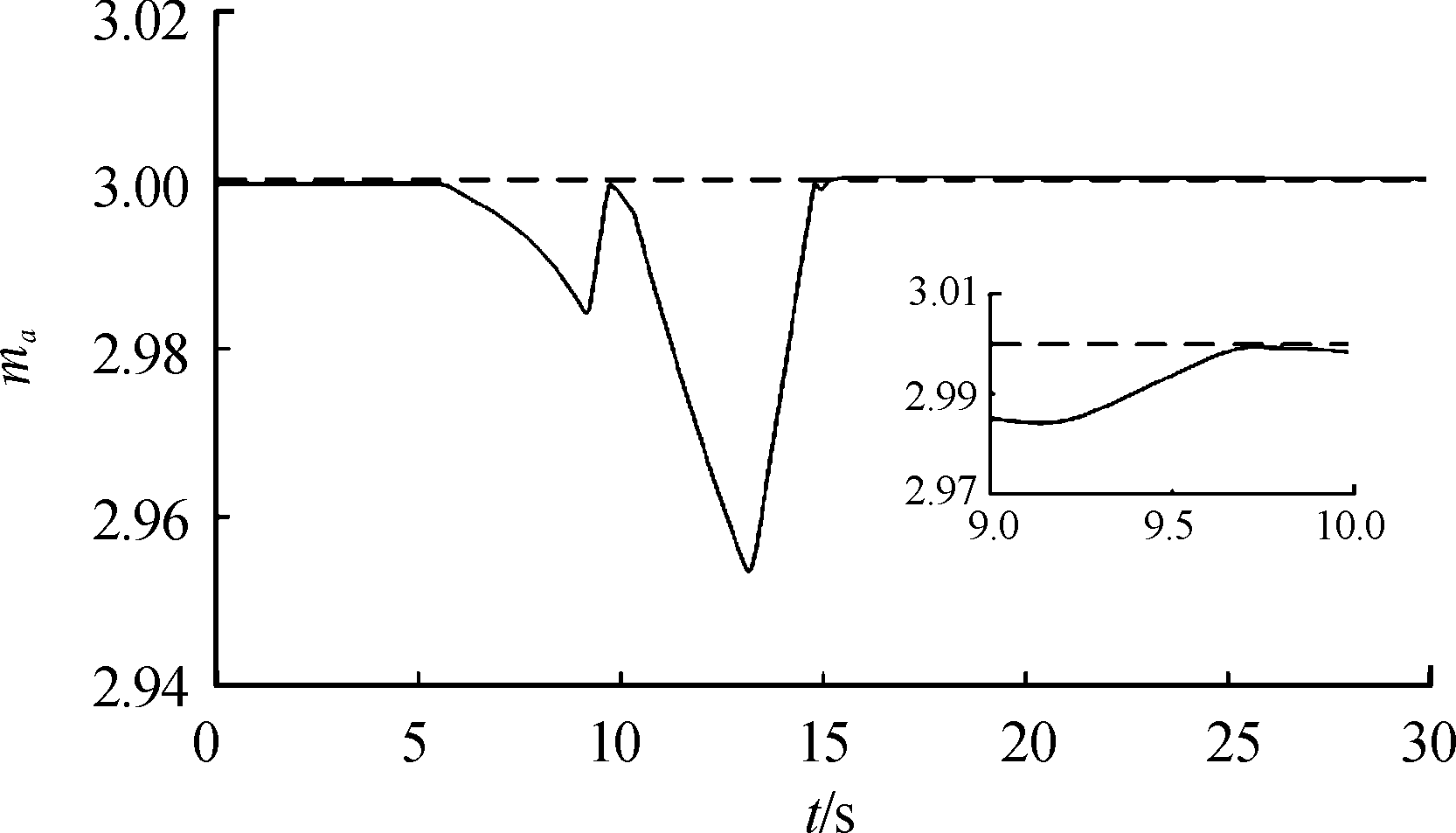
图10 马赫数响应曲线
Fig.10 Response of Mach
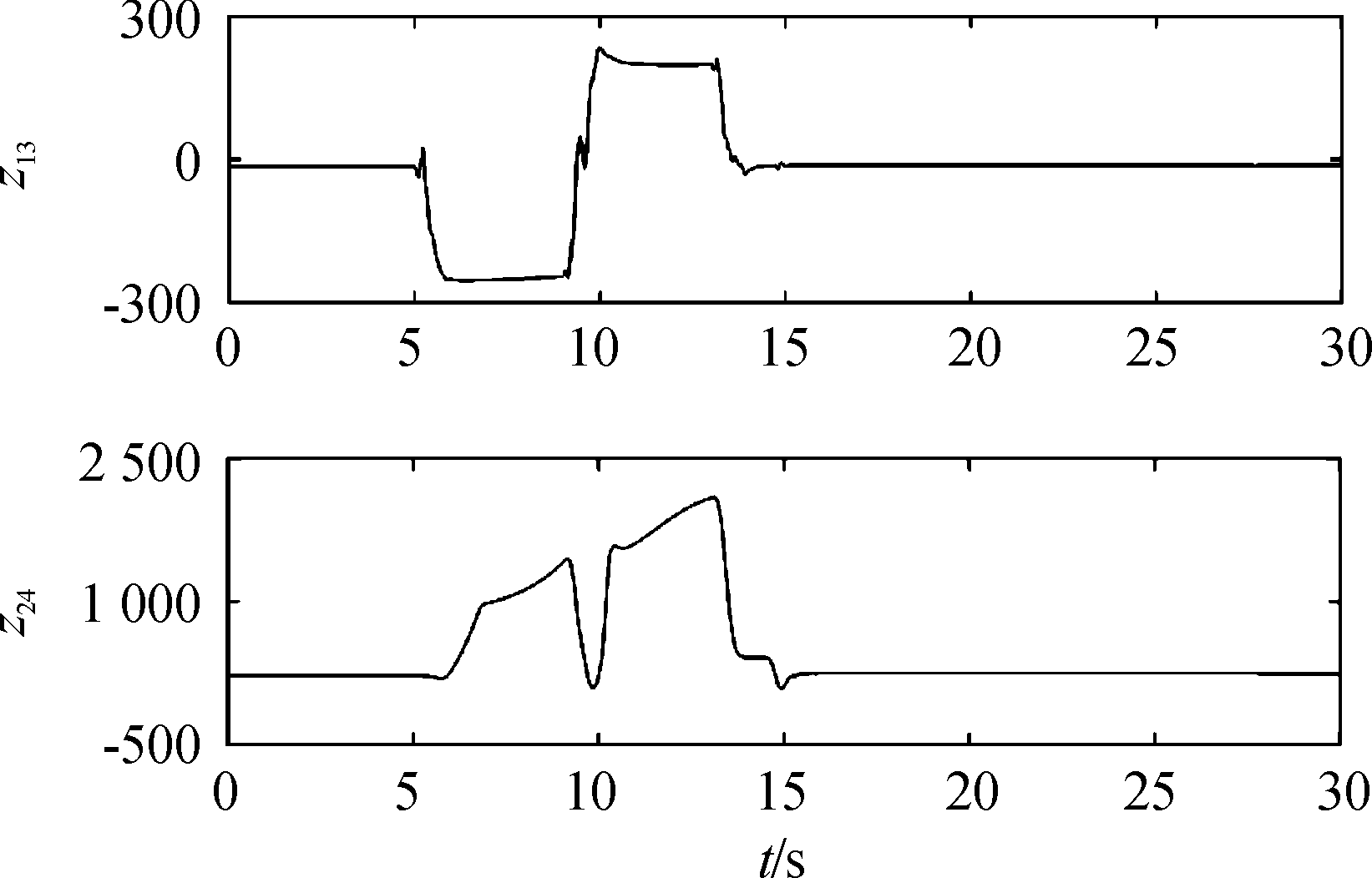
图11 过载通道和马赫数通道总扰动估计曲线
Fig.11 Estimation of overall disturbance of overload loop and Mach loop
从图7可以看出，导弹能够快速的跟踪大过载指令，过载指令从1上升到10的时间为0.75 s，超调量为0.5%，稳态误差小于0.1%；同时从图8可以看出，在导弹跟踪过载指令过程中，舵偏没有抖振现象，其中舵面在控制指令突变时变化较大，这是由于控制指令突变会导致扰动估计值z13发生较大变化，而z13又被直接引入到舵偏指令中。从图8、图9可以看出，导弹平飞时，余气系数af约为2.0，当导弹做大过载机动时，导弹的平衡攻角约为10.76°和-10.7°，此时冲压发动机进气道捕获的进气量迅速减少，余气系数一直处于1.1，即冲压发动机处于最大供油状态，其中余气系数在9.6～10 s，燃油流量在9～10 s期间发生较大的变化，这是由于过载指令在9 s时刻由正10变为-9，攻角从10.76°变为-10.7°，在这一过程中，攻角的绝对值减小，冲压发动机进气道捕获的空气量增加，允许的供油流量增加，导弹飞行马赫数逐渐跟上马赫数跟踪指令，因而余气系数也逐渐增大。从图10可以看出，在导弹跟踪过载指令过程中，马赫数有明显的下降，这种情况并不是由于过载通道和马赫数通道耦合造成的；而是由于导弹做大过载机动时，导弹攻角快速增大，这使得冲压发动机进气道能捕获的进气量下降，根据式(3)，即使余气系数af一直处于最小值1.1，发动机允许的供油量也会减小，相应的发动机推力也较小，从而导致导弹速度下降，从图9也可以看出马赫数偏差较大时，发动机处于最小余气系数工作状态。从图11可以看出，导弹做大过载机动时，过载通道和马赫数通道扰动量都比较大，这主要是气动参数和发动机性能参数都对攻角敏感，攻角的快速变化会使得这两个通道的扰动显著增加。
5 结论
1) 控制器能够快速准确跟踪过载和马赫数控制指令，且通道之间耦合较小，舵面和供油量不存在抖振现象。
2) ESO观测器能够对系统中的扰动进行有效估计，将估计值动态补充到控制器中可显著提高控制器抗扰动能力和系统鲁棒性能。
3) 仿真发现冲压发动机导弹在长时间大过载机动时，导弹速度下降，严重时有可能导致超出发动机正常工作状态，后续将进一步研究考虑冲压发动机稳定工作边界的大过载机动控制问题。
[1] 吴立刚，安昊，刘健行，等.吸气式高超声速飞行器控制的最新研究进展[J].哈尔滨工业大学学报，2016，48(10)：1-16.
WU Ligang，AN Hao，LIU Jianxing，et al.Recent Progress in Control of Air-breathing Hypersonic Vehicles[J].Journal of Harbin Institute of Technology,2016，48(10)：1-16.
[2] MA Liqun，DUAN Chaoyang.Review on Development of Guidance and Control for Long-Range Tactical Missile Based on Ramjet Technique[J].Aero Weaponry，2016，2(04):17-23.
[3] LI Huifeng.The Guidance and Control Technology for Hypersonic Vehicle[M].Beijing：China Aerospace Publishing House，2012.
[4] 王勇，张艳，白辰，等.吸气式高超声速飞行器制导与控制方法综述[J].兵器装备工程学报，2017，38(04)：78-82.
WANG Yong，ZHANG Yan，BAI Chen，et al.Review of Guidance and Control Approaches for Air-Breathing Hypersonic Vehicle[J].Journal of Ordnance Equipment Engineering，2017，38(04)：78-82.
[5] Famularo D I，Valasek J，Muse J A，et al.Adaptive Control of Hypersonic Vehicles Using Observer-Based Nonlinear Dynamic Inversion[C]//2018 AIAA Guidance，Navigation，and Control Conference.2018：0843.
[6]WANG Ling，LIU Xiangdong，SHENG Yongzhi，et al.Disturbance Observer Based Exponential Time-Varing Sliding Mode Flight Control Design for Cruise Vehicle[J].Journal of Astronautics，2013，34(08)：1091-1099.
[7] Liu X，Zhang Y，Wang S，et al.Backstepping Attitude Control for Hypersonic Gliding Vehicle Based on a Robust Dynamic Inversion Approach[J].Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2014，228(8)：543-552.
[8] Ye L，Zong Q，Crassidis J L，et al.Output-Redefinition-Based Dynamic Inversion Control for a Nonminimum Phase Hypersonic Vehicle[J].IEEE Transactions on Industrial Electronics，2018，65(4)：3447-3457.
[9] Sagliano M，Mooij E，Theil S.Adaptive Disturbance-Based High-Order Sliding-Mode Control for Hypersonic-Entry Vehicles[J].Journal of Guidance Control Dynamics，2017，40(3)：1-16.
[10] CHEN Zengqiang，LIU Junjie，SUN Mingwei.Overview of a Novel Control Method：Active Disturbance Rejection Control Technology and its Practical Applications[J].CAAI Transaction on Intelligent Systems，2018，13(06)：865-877.
[11] HAN Jingqing.Active Disturbance Rejection Control Technology[M].Beijing：National Defense Industrial Press，2008.
[12] CHENG Mingzhi WU Yunjie，MA Fei.Sliding Mode Auto-Disturbance Rejection Control of Hypersonic Vehicle under Disturbance[J].Journal of System Simulation，2017,29(10)：2391-2396，2406.
[13] FANG Xue，YANG Wenjun，FAN Zheng，et al.Multi Power Sliding Mode Control of Hypersonic Flight Vehicle[J].Journal of Solid Rocket Technology，2018，41(02)：258-264.
[14] CHEN Chen， MA Guangfu， SUN Yanchao，et al.Recursive Sliding Mode Control for Hypersonic Vehicle Based on Nonlinear Disturbance Observer[J].ACTA Armamentarii，2016，37(05)：840-850.
[15] Sun M，Wang Z，Chen Z.Practical Solution to Attitude Control Within Wide Envelope[J].Aircraft engineering，2014，86(2)：117-128.
[16] 霍斯琦，范世鹏，高琦，等.基于自抗扰的再入飞行器阻力加速度跟踪技术[J].兵器装备工程学报，2019，40(01)：154-158.
HUO Siqi，FANG Shipeng，GAO Qi，et al.Drag Profile Tracking Law Based on Active Disturbance Rejection Control Theory for Reentry Vehicles[J].Journal of Ordnance Equipment Engineering，2019，40(1)：154-158.
[17] SUN Xiaosong，MU Yuqiang，SHEN Haibin，et al.Study on Control and Verification Method of Ramjet Engine[J].Aerospace Control，2017，35(04)：33-36.
[18] LI Yan，Mu Chunhui，NIE Lingcong.Multi-Variable Robust Stability Control for Wide Envelope Ramjet Based on μSynthesis[J].Journal of Propulsion Technology，2019，40(06)：1409-1418.
High Overload Maneuver Control of Ramjet Missile Based on Active Disturbance Rejection Control
Citation format:SHI Yuyang，PENG Xuefeng，QU Lifeng, et al.High Overload Maneuver Control of Ramjet Missile Based on Active Disturbance Rejection Control[J].Journal of Ordnance Equipment Engineering,2021,42(07):13-18.