刚性包带式星箭锁紧机构分离性能研究
1 引言
航天科技发展初期，星箭间的连接与分离主要采用对接面均布爆炸螺栓的方式，当螺栓数量较多，单点失效环节增加，分离可靠性难以保证[1-3]。随后世界各国相继研发多种柔性包带机构，其由扁平薄钢带、V型卡块、弹簧系统和爆炸螺栓等相关零件组成[4-5]，截至目前柔性包带广泛应用于星箭间的连接与分离，同时国内外学者对柔性包带的理论及其性能研究工作已经较为成熟[6-8]。然而火工式柔性包带依然存在承载性能弱、分离冲击大、动态包络大和无法重复使用等不足，因此近年来一种非火工式刚性包带逐渐引起国内外学者的重视。刚性包带凭借其特殊的结构设计和变形方式，使其依靠包带自身较大的弹性变形实现星箭连接与分离功能，摆脱了传统爆炸螺栓驱动解锁分离。国外学者Lancho等[9]设计一种卡环分离系统(clamp ring separation system)，并通过测试证明CRSS可以满足使用要求；欧美各宇航公司也相继开展了刚性包带机构的研究，并逐步替代传统火工式柔性包带，成为国外运载火箭主要使用的星箭分离机构。国内于兵等[10]发明了一种采用整体铝制锻环制造的小包络、低冲击、整环式刚性包带；王林刚等[11]针对整环式刚性包带分离过程进行动态仿真分析并研究了包带直径、摩擦因数和V型角对分离性能的影响。
刚性包带采用刚度较大的厚铝板整体锻造而成，同柔性包带相比，它的承载能力更强，动态包络更可控，分离冲击更小，安装更方便，同时可以重复利用。但是刚性包带系统力学行为复杂，各构件之间存在接触、摩擦、空隙等现象，接触非线性和几何非线性显著[12-13]。因此，刚性包带机构的建模仿真分析及其性能研究将是星箭连接和分离技术研究的热点与重点。
2 仿真模型及方法
新型刚性包带机构主要部件包括：刚性包带、端头、分离弹簧、限位弹簧、卫星对接框和火箭对接框等，如图1所示，其中分离弹簧主要用于实现卫星的弹射分离；限位弹簧起到控制解锁后包带最大径向位移的作用，防止脱离后的包带与卫星相关附件发生干涉。包带自由状态直径为1 480.5 mm，V型槽角度15°，对接框直径选取1 194 mm运载火箭标准接口参数；分离弹簧沿对接框均匀分布4个，刚度系数为80 N/mm，限位弹簧设置于两极端头处，刚度系数0.5 N/mm。模型材料选取锻铝2A14-T6航空级铝合金(旧牌号LD10)，密度为2 790 kg/m3，弹性模量为70.6 GPa，泊松比0.3，屈服强度415 MPa[13]。刚性包带自由状态下两极端头间夹角较大，施加预紧力后包带沿着径向发生较大弹性变形，利用弹性变形能实现连接与分离功能。
图1 刚性包带系统部件组成示意图
Fig.1 Components of band system
基于ABAQUS/Explicit求解器，将刚性包带安装及解锁分离过程仿真分析设置以下4个计算分析步，如图2所示。① 下压过程：上对接框垂直向下移动100 mm，下对接框保持固定，模拟分离弹簧初始受压，下压时间30 s；② 推进过程：对两侧包带设置径向位移边界条件，将其顶推至对接框，使得包带发生弯曲变形，直至包带V型槽与对接框V型缘相互接触，推进时间30 s。③ 预紧过程：对端头螺栓孔施加水平方向集中力模拟螺栓预紧过程，大小为10 kN，使得包带V型槽夹紧上下对接框，其中预紧力加载时间10 s，预紧力恒定时间20 s；④ 解锁分离过程：刚性包带属于典型冷分离机构，不存在以往爆炸螺栓式解锁造成的局部高频、高量级冲击，其分离冲击主要来源于对接框间储存的应变能和刚性包带自身因弹性变形所储存的变形能。因此通过设置预紧力加载幅值曲线可以很好地模拟剪切解锁过程，使得预紧力在0.001 s内降为0，利用刚性包带自身弹性变形能实现解锁后的快速脱离功能，同时在分离能源(分离弹簧)的推动下，卫星对接框实现弹射分离。
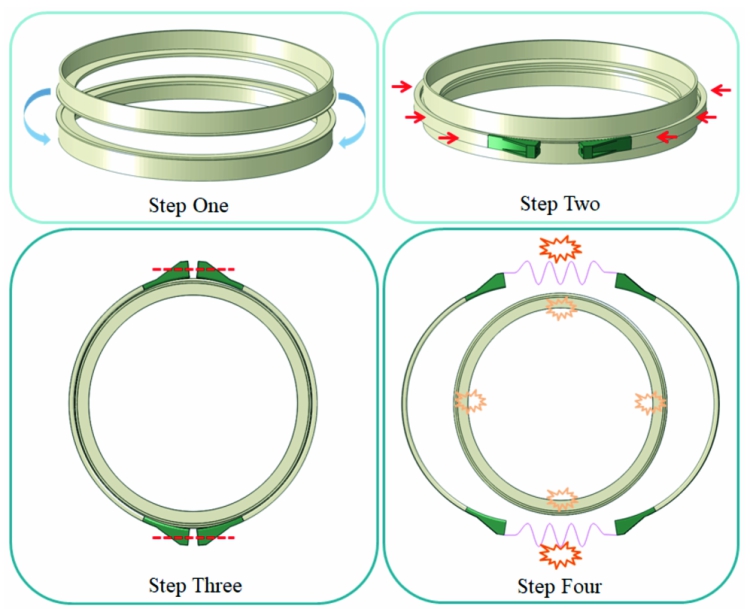
图2 分析步设置示意图
Fig.2 Analysis step settings
基于上述分析步，模型边界条件设置如图3所示。上、下对接框内表面分别与参考点RP1、RP2建立耦合约束，4个端头螺栓孔面分别与参考点RP21、RP22、RP23、RP24进行耦合，各个分析步中边界条件的设置见表1。
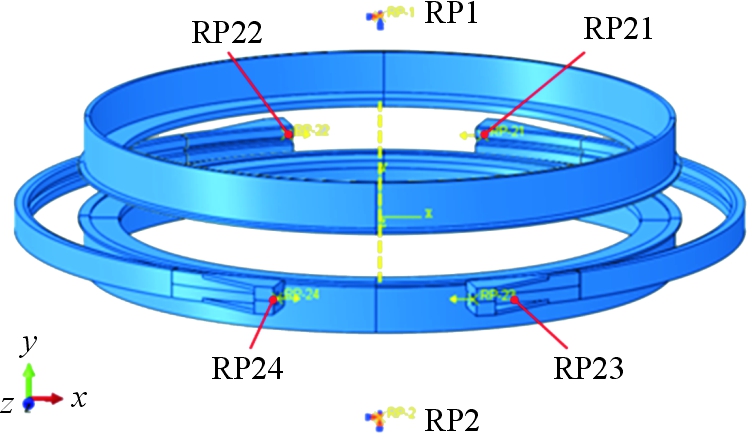
图3 边界条件设置示意图
Fig.3 Boundary condition settings
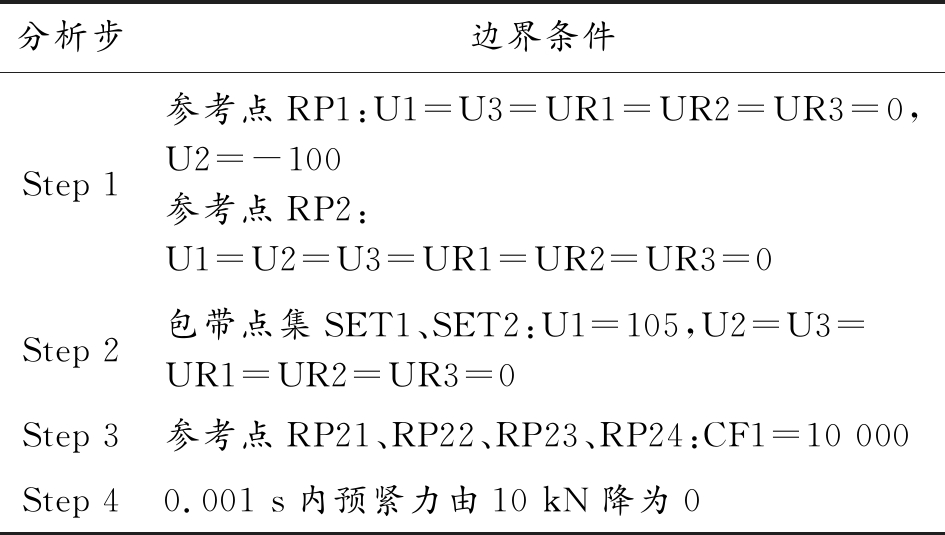
表1 各个分析步的边界条件设置
Table 1 Boundary condition settings for each analysis step
刚性包带系统共涉及3对接触面，分别为V型槽与V型缘间的2对接触面(以下简称C-T接触面)和对接框间的接触面(简称S-X接触面)，其中C-T接触面采用通用接触边界条件，S-X接触面采用Surface-to-Surface接触边界条件。各接触对均采用罚函数法定义摩擦属性，S-X接触面摩擦因数0.3，C-T接触面0.15。刚性包带和对接框采用C3D8R单元，端头采用C3D10M单元，网格总数量 652 604个。
3 仿真模型校验
3.1 轴向接触载荷关系式
刚性包带加载过程中，在各接触部件间正压力、摩擦力、弹簧作用力和螺栓预紧力的共同作用下，整套机构处于静力平衡状态。预紧力过大，导致安装过程中结构屈服破坏；预紧力过小，无法满足初始轴向接触载荷预紧条件，存在安全隐患。轴向接触载荷作为评判星箭连接承载要求的重要指标之一，因此建立起螺栓预紧力与轴向接触载荷间的关系对指导工程实践具有重要意义。
包带系统半圆周受力如图4(a)所示，横截面受力如图4(b)所示，并在计算中作以下假设：
1) 对接框连接面接触应力沿圆周方向均匀分布；
2) 上下对接框结构尺寸相同，即V型槽对上下V型缘压力相同；
3) 刚性包带径向施加的压力沿着圆周方向均匀分布。
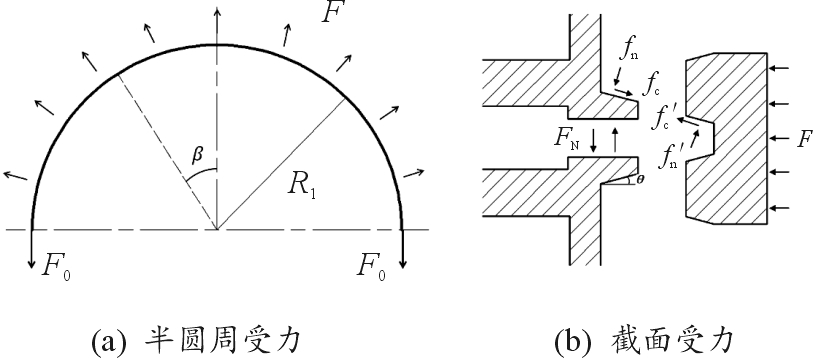
图4 包带系统力学分析示意图
Fig.4 Mechanical analysis ofband system
如图4(a)所示，设端头螺栓预紧力为F0，则有：
2F0=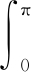
F·R1sinβdθ
(1)
式中: F为单位弧长包带所受的径向压力；R1为包带安装后的半径； θ为V型槽和V型缘倾角。如图4(b)所示，对刚性包带进行受力平衡分析：
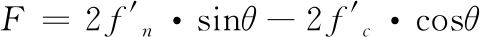
(2)
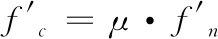
(3)
式中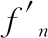
和f′c分别为单位弧长包带所受的正压力与摩擦力；μ为接触面摩擦因数。由式(1)～(3)可以建立螺栓预紧力F0与正压力
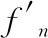的关系式：
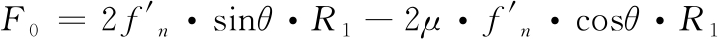
(4)
如图4(b)所示，上、下对接框结构尺寸相同，受力相同，对上对接框：
FN+FC=fncosθ+fcsinθ
(5)
fc=μ·fn
(6)
式中: FN为单位弧长对接框连接面所受的压力； FC为单位弧长对接框所受的弹簧作用力； fn为单位弧长包带与对接框接触面所受的正压力； fc为静摩擦力。考虑到压力FN沿连接面径向呈不均匀分布，其横截面变形如图5所示，设其有效接触宽度为l，连接面宽度为d，包带系统的轴向接触载荷为T，则有：
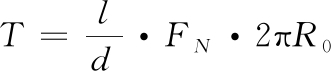
(7)
式中R0为对接框半径。联立式(5)～式(7)可以得出系统轴向接触载荷T与正压力fn的关系式：
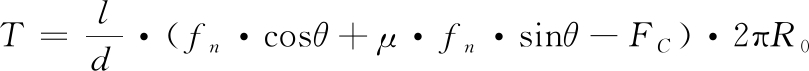
(8)
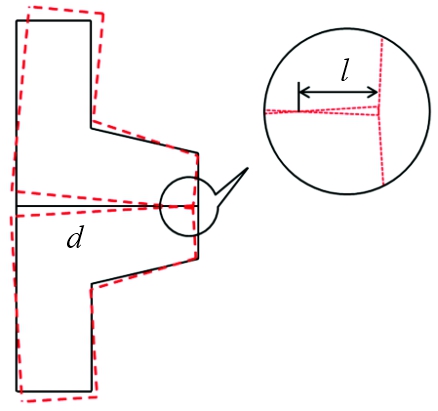
图5 对接框变形图
Fig.5 Deformation diagram of butt joint frame
已知fn和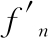
为相互作用力，大小相等。通过式(4)和式(8)可以得出螺栓预紧力与系统轴向接触载荷之间的解析表达式：
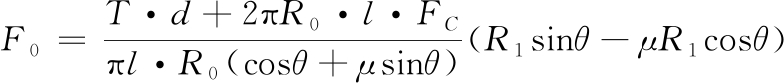
(9)
3.2 理论值与仿真值对比
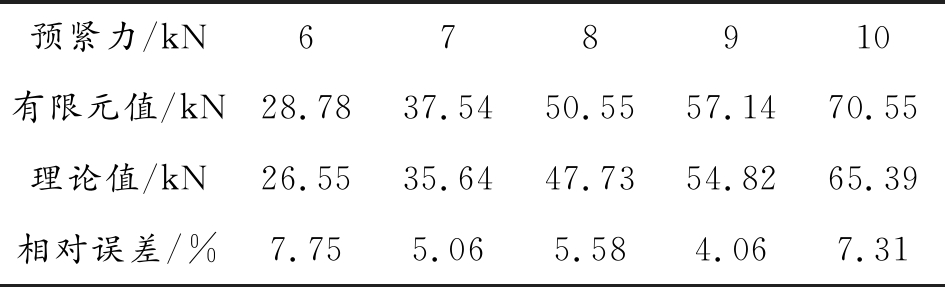
包带系统轴向接触载荷随时间的变化关系如图6所示。下压过程中，通过位移加载方式使得上对接框移动至与下对接框零接触的临界状态，完成分离弹簧初始压缩，因此载荷值为0 kN；推进过程中，V型槽逐步与V型缘产生接触，载荷呈波动增长趋势；预紧过程中，随着螺栓预紧力的增加，V型槽逐渐夹紧对接框，轴向接触载荷值逐渐增加，并最终稳定于70.55 kN。此时从模型中提取有效接触宽度l值为6.80 mm，应用预紧力与轴向接触载荷的关系式计算得到理论轴向接触载荷值为65.39 kN，有限元结果与理论计算结果对比误差为7.31%。不同预紧力下有限元计算结果与理论结果列于表2，从表2可以看出，理论模型得到的轴向接触载荷值均略小于有限元仿真值，同时两者误差均在10%以内，计算结果基本吻合，验证了有限元模型及其分析方法的有效性。
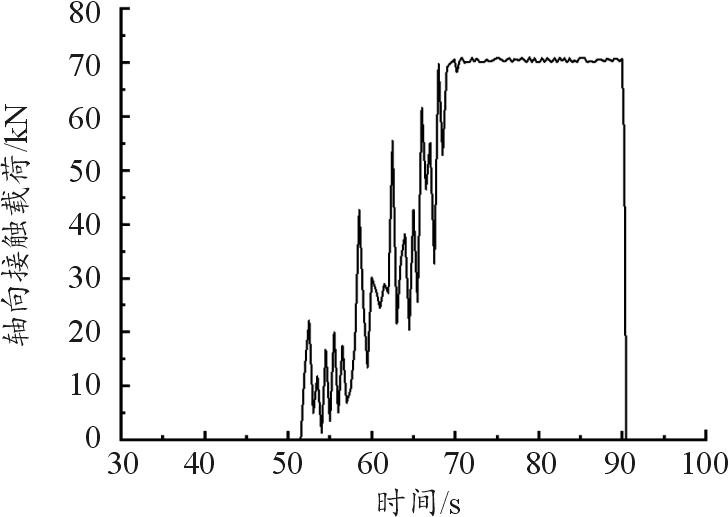
图6 轴向接触载荷时变曲线
Fig.6 Time varying curve of axial contact load
表2 不同预紧力下有限元值与理论值对比
Table 2 Comparison of finite element and theoretical values under different preloads
4 仿真结果分析
4.1 分离时间
分离时间指分离过程中解锁机构启动后包带与对接框发生脱离，当包带距离对接框最近的特征点刚好在V型缘的边界处所用的时间。从包带内壁侧选取特征点位置如图7所示，通过特征点位移时变曲线对分离时间展开计算。
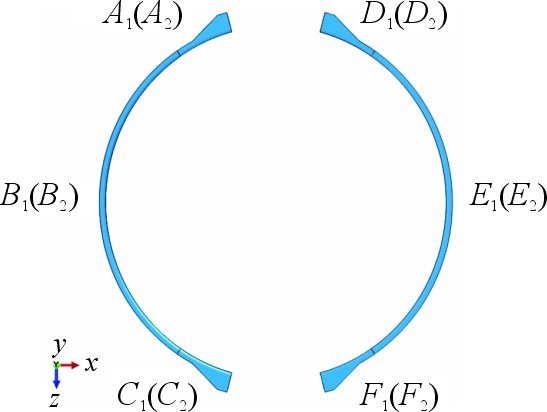
图7 特征点位置示意图
Fig.7 Location of feature points
考虑到模型左右两侧边界条件设置相同，故仅提取测点A1/A2、B1/B2、C1/C2位于X-Z平面内的位移时变曲线如图8。计算得端头特征点A1/A2/C1/C2脱离时间4.1 s，为最先脱离对接框的特征点；最后脱离对接框的特征点B1/B2脱离所用时间26.8 s，该时间即为包带分离时间。其中分离不同步时间为最先脱离对接框特征点与最后脱离对接框特征点时间差值22.7 s。
刚性包带成功分离时的临界状态，即B1/B2/E1/E2特征点刚好移动至V型缘的边界处，此时端头特征点A1/C1/D1/F1沿U1方向的位移分量为59.15 mm，沿U3方向的位移分量为78.50 mm；包带特征点B1/E1仅存在U1方向的位移值为7.25 mm。
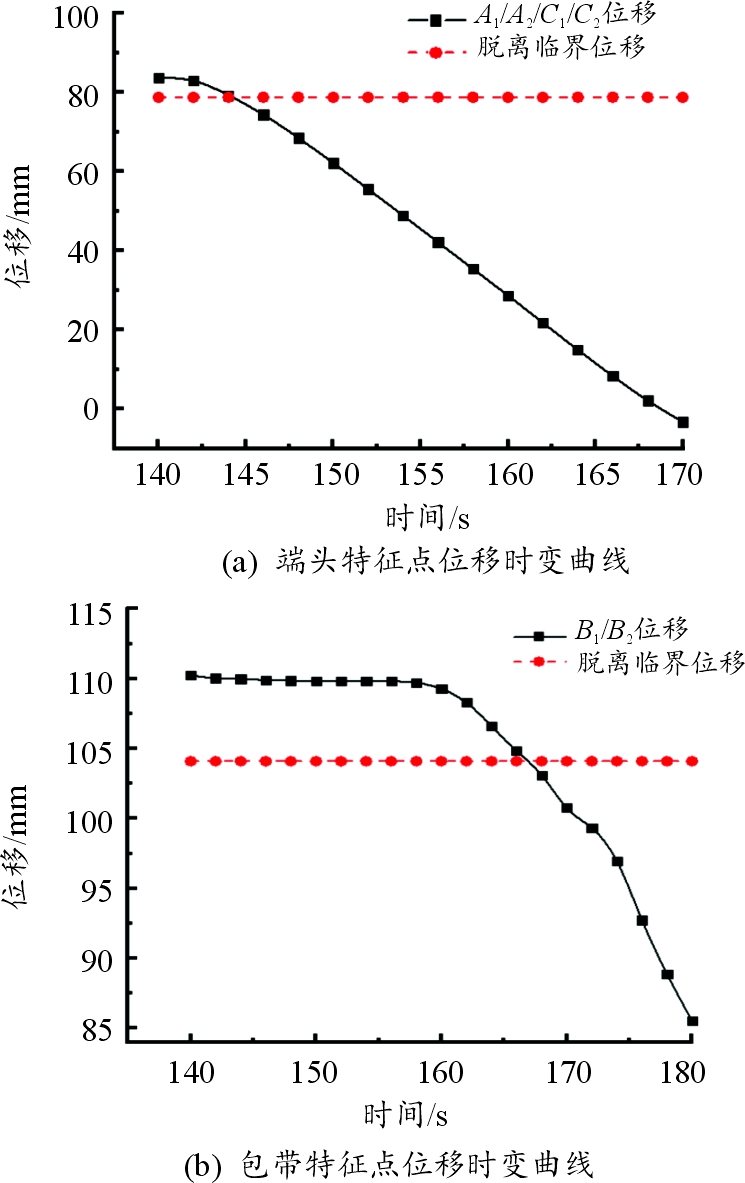
图8 特征点位移随时间的变化关系曲线
Fig.8 Variation of feature point displacement with time
4.2 动态包络
动态包络是指包带在分离过程中运动轨迹的最大轮廓，如图9所示。以对接框几何中心O为参考中心，绘制包带最大轮廓与卫星底面最大轮廓。其中卫星半径R选取990 mm，安全间隙极限值h选取50 mm。设包带解锁后的最大包络距为Nmax，则Nmax应满足：
Nmax≤R-h=940 mm
(10)
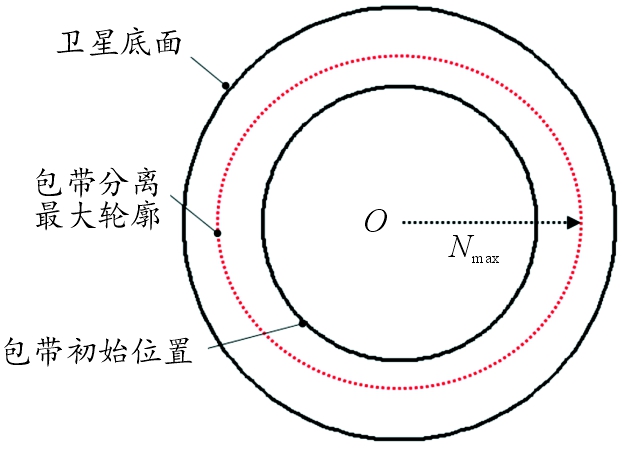
图9 包带包络示意图
Fig.9 Schematic diagram of tape envelope
沿包带外壁均匀选取18个标记点，用这些标记点在分离过程中的最大径向位移绘制包带的包络，如图10所示。从图10可以看出，分离后的刚性包带呈两极稍扁、中间略鼓的椭圆形；包带最小包络距位于两极端头处，其值为787.87 mm；最大包络距位于距离两极端头最远处，其值为802.15 mm。
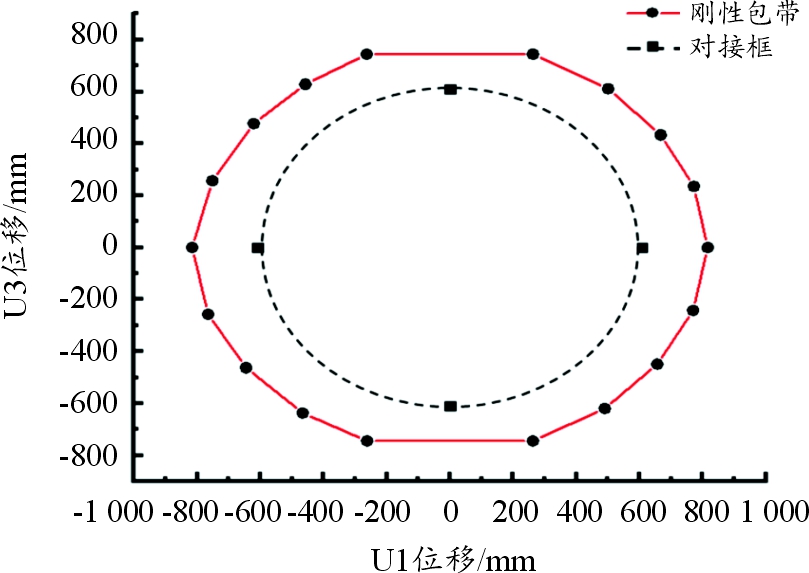
图10 包带动态包络曲线
Fig.10 Dynamic envelope curve of band
5 分离性能影响因素分析
5.1 螺栓预紧力
分离时间随预紧力的变化关系如图11所示，显然随着预紧力的增加，分离时间呈先递增后递减的趋势。当预紧力等于9 kN时，时间达到峰值28.0 s；预紧力小于9 kN时，随着其值的增加V型槽与V型缘接触面的正压力和摩擦力逐渐增加，摩擦损耗的能量不断增大，而此时系统的应变能增长较缓慢，导致分离时间有所延长；预紧力超过9 kN后，摩擦损耗能趋于恒定，预紧力的增加会使得V型槽逐渐夹紧对接框，系统应变能增加，解锁后包带分离动能增加，分离时间降低。系统摩擦损耗能与应变能随预紧力的变化趋势如图12所示。
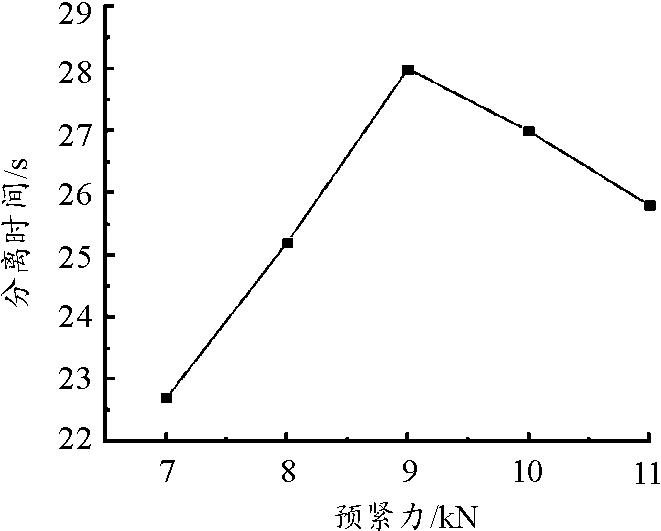
图11 分离时间随预紧力的变化关系曲线
Fig.11 Variation curve of separation time with preload
图12 能量随预紧力的变化趋势直方图
Fig.12 Histogram of variation trend of energy with preload
图13所示为包带包络距随预紧力的变化关系。预紧力取值9 kN时，包络距均出现降低，与前述预紧力对分离时间的影响相对应。从整体变化趋势上看，预紧力的增加使得最大包络距减小，最小包络距增大，原因在于随着预紧力的增加，端头应变能的增长速率大于包带本体应变能的增长速率，如图14所示，导致分离过程中端头的脱离速度大于包带中间位置的脱离速度，即单位时间内端头的位移值大于包带中间区域位移值。同时预紧力的改变对最小包络距的影响小于其对最大包络距的影响，预紧力由7 kN增加到11 kN，最小包络距增大了1.3%，最大包络距减小了3.9%。
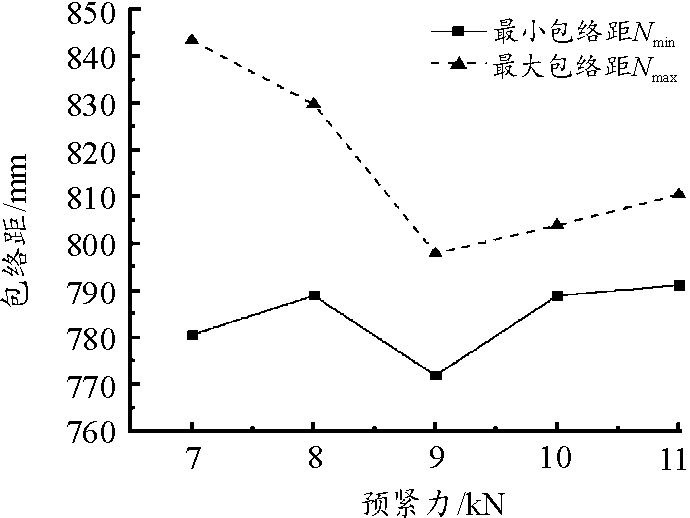
图13 包络距随预紧力的变化关系曲线
Fig.13 Variation curve of envelope distance with preload
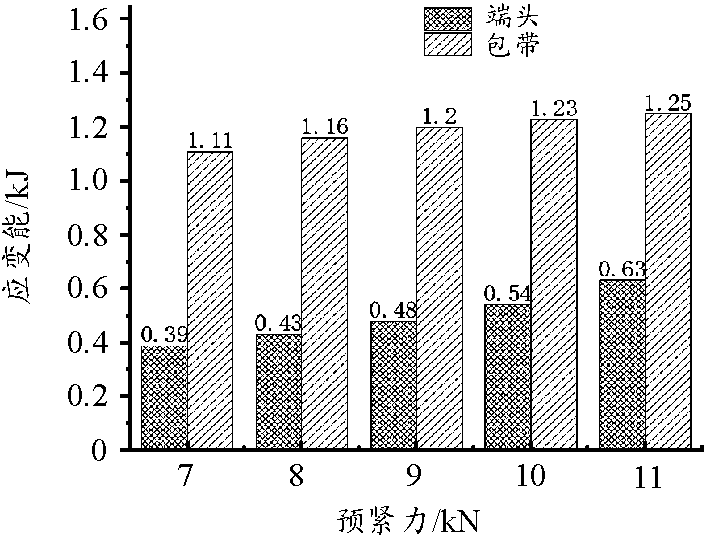
图14 应变能随预紧力的变化趋势直方图
Fig.14 Variation trend of strain energy with preload
5.2 摩擦因数
刚性包带系统共涉及3对接触面，分别为包带V型槽与对接框V型缘的2对接触(C-T接触面)、对接框间的接触(S-X接触面)。其中C-T接触面的摩擦因数决定了包带解锁后的径向移动速度，影响分离时间。
在ABAQUS/Interaction Property窗口中对C-T接触面摩擦因数μ进行修改并仿真。当μ取0.4时，星箭分离出现故障，刚性包带发生单侧局部卡滞现象，如图15(a)所示；μ取0.5时，解锁后两侧包带均未成功脱离而发生卡滞，如图15(b)所示。其原因在于包带解锁后，对接框局部应变能瞬间释放所产生的轴向冲击力和分离弹簧施加的轴向作用力均集中于包带中间区域，使得中部区域C-T接触面正压力和静摩擦力急剧增加，当摩擦因数μ较大时，正压力与摩擦力在U1方向上的分力极短时间内达到平衡状态，导致包带与对接框发生卡滞。
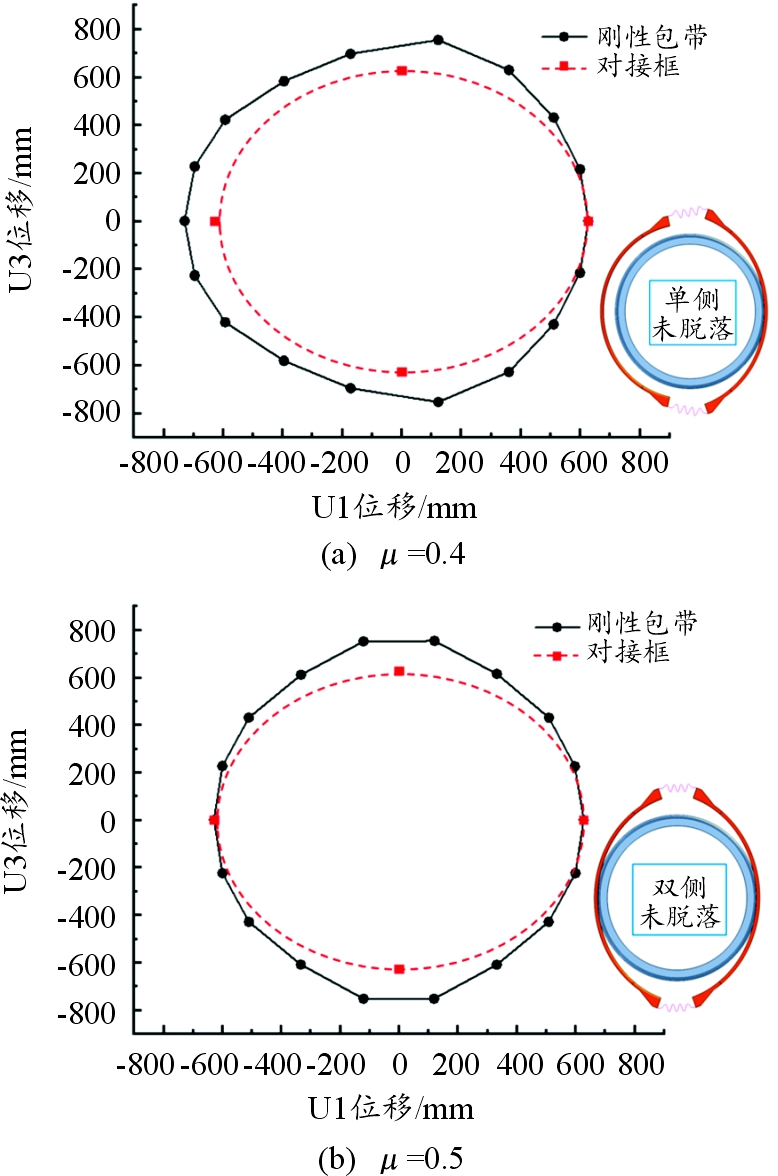
图15 分离故障示意图
Fig.15 Schematic diagram of separation fault
分离时间随摩擦因数的变化关系如图16所示。因数由0增加至0.35，分离时间增加了37.90 s，显然摩擦因数的改变对分离时间影响极为显著，因此航天工程中通常采用在接触面间涂抹二硫化钼的方式进行润滑。摩擦因数对分离时间造成的影响，可以从能量耗散的角度进行解释。随着摩擦因数的增加，摩擦耗散的热量持续上升，系统整体能量不断降低，导致包带分离动能降低，分离所需时间增加。不同摩擦因数下的系统摩擦耗散能如图17所示。
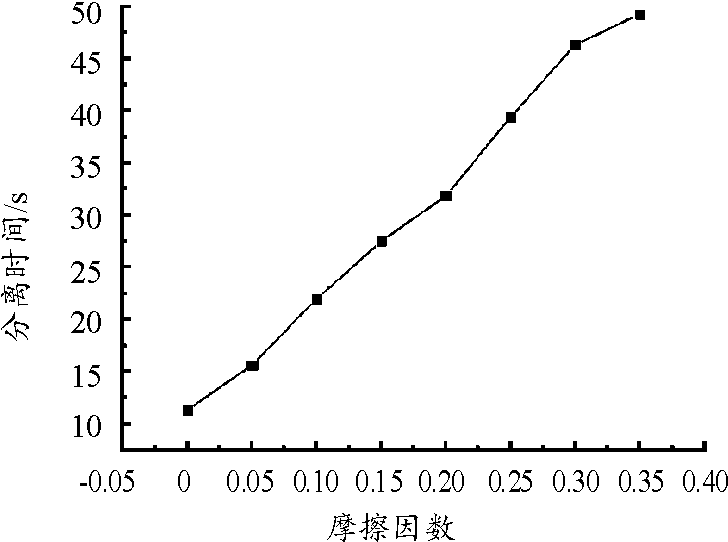
图16 分离时间随摩擦因数的变化关系曲线
Fig.16 Variation of separation time with friction coefficient
图17 摩擦耗散能随摩擦因数变化直方图
Fig.17 Histogram of friction dissipation energy with friction coefficient
包带包络距随摩擦因数的变化关系如图18所示，摩擦因数由0.10增加到0.30，最小包络距减小了6.8%，最大包络距减小了4.3%，摩擦因数的增加会降低包带的包络距，同时对最小包络距的影响大于其对最大包络距的影响。由前述分析可知，摩擦因数增加会造成摩擦损耗能增加，包带分离动能降低，有利于减小包带包络，但因数值过大也会导致包带与对接框发生卡滞现象影响分离。
5.3 分离弹簧刚度
图19所示为分离时间随弹簧刚度的变化关系，随着弹簧刚度的增加分离时间逐渐减小，原因在于弹簧刚度的增加使得弹簧单位压缩量所储存的势能增多，解锁后转化为包带分离动能增加，分离所需时间降低。分离弹簧刚度的改变对分离时间影响较大，弹簧刚度大，分离所需时间少，系统产生的振动与冲击较高，因此应根据实际航天工程需要，去寻求分离时间与系统稳定性两者之间的阈值点。
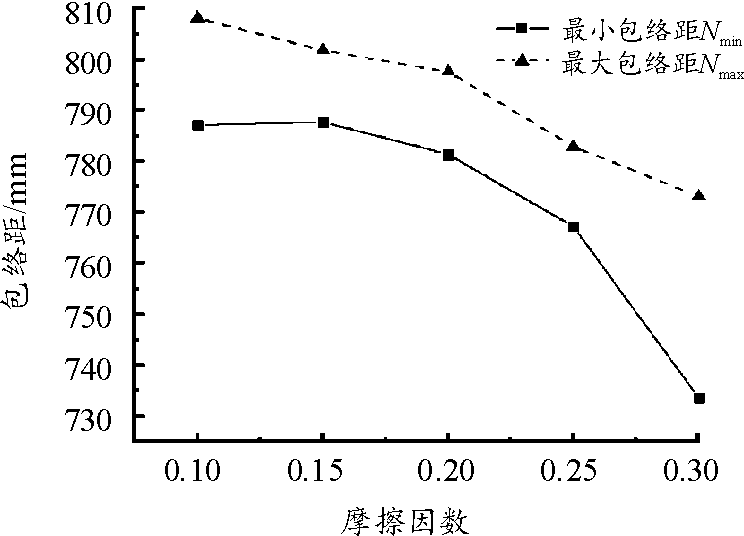
图18 包络距随摩擦因数的变化关系曲线
Fig.18 Variation of envelope distance with friction coefficient
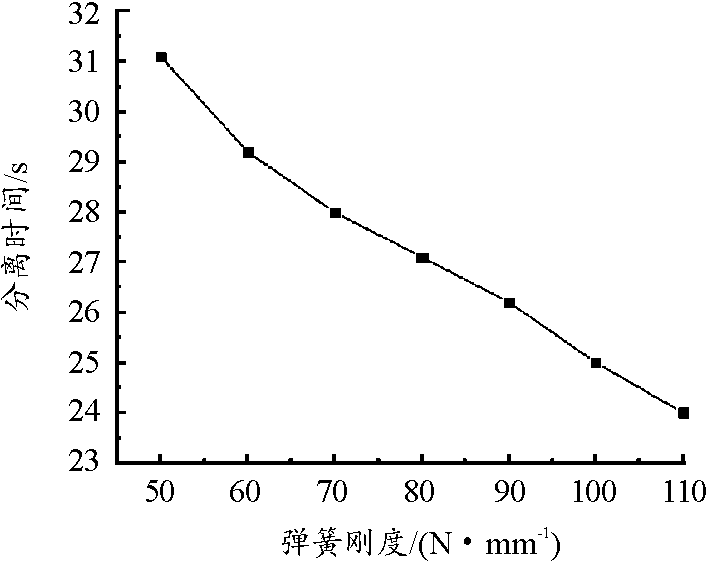
图19 分离时间随弹簧刚度的变化关系曲线
Fig.19 Variation of separation time with spring stiffness
包带包络距随弹簧刚度的变化关系如图20所示，弹簧刚度对最小和最大包络距影响均较弱，刚度值由70 N/mm增加到110 N/mm，包络距均有所增加，最小包络距仅增加了0.43%，最大包络距仅增加了0.63%。
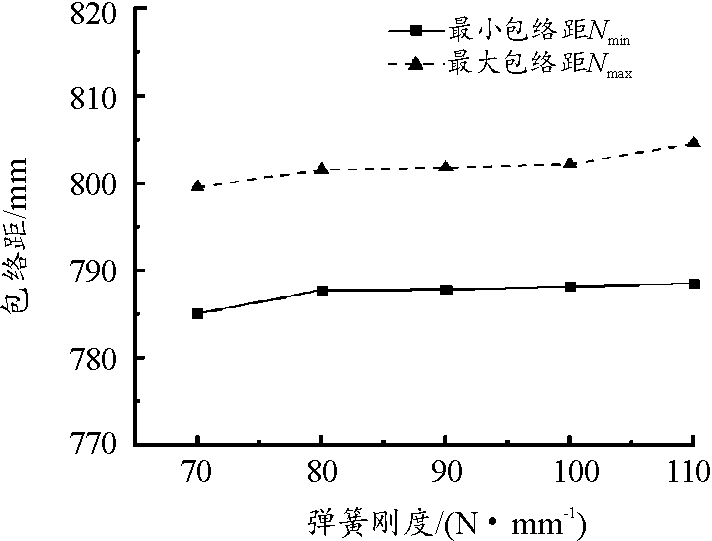
图20 包络距随弹簧刚度的变化曲线
Fig.20 Variation of envelope distance with spring stiffness
6 影响因素显著性评估
采用Min-Max标准化将上述各影响因素的原始数据转换为无量纲化指标测评值，即各指标值都处于同一个数量级别，以便进行显著性分析。Min-Max标准化是对原始数据的线性变换，将结果值映射到[0，1]区间，转换函数公式如下：
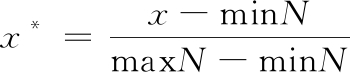
(11)
式中: x为样本数据值，maxN和minN分别为样本数据最大值、最小值。
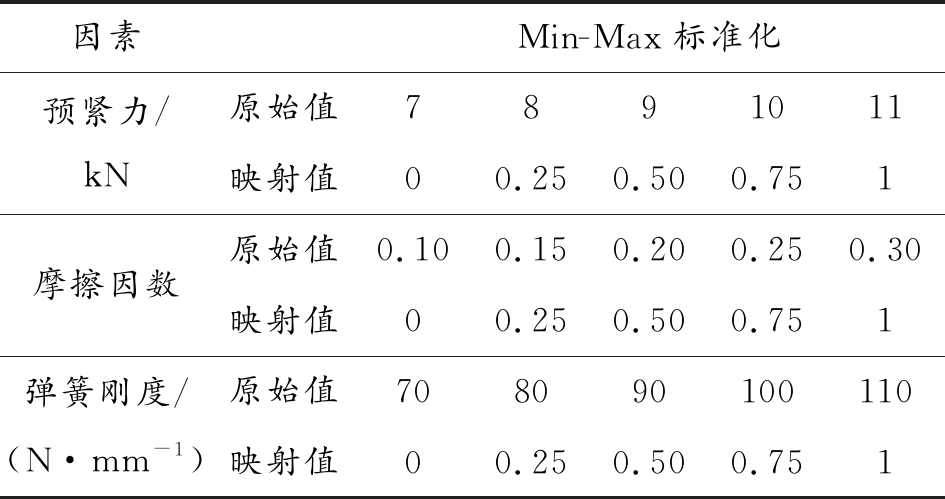
将预紧力、摩擦因数和弹簧刚度的取值范围映射到[0，1]区间，整理成表，如表3。
表3 样本数据的标准化处理
Table 3 Standardized processing of sample data
如图21所示，在给定的取值范围内，各因素对分离时间的影响程度按从高到低的顺序分别为C-T接触面摩擦因数、分离弹簧刚度、螺栓预紧力。摩擦因数值增加0.2，分离时间延长24.3 s；刚度值增加40 N/mm，时间缩短4.0 s；预紧力增加4 kN，时间延长3.1 s。
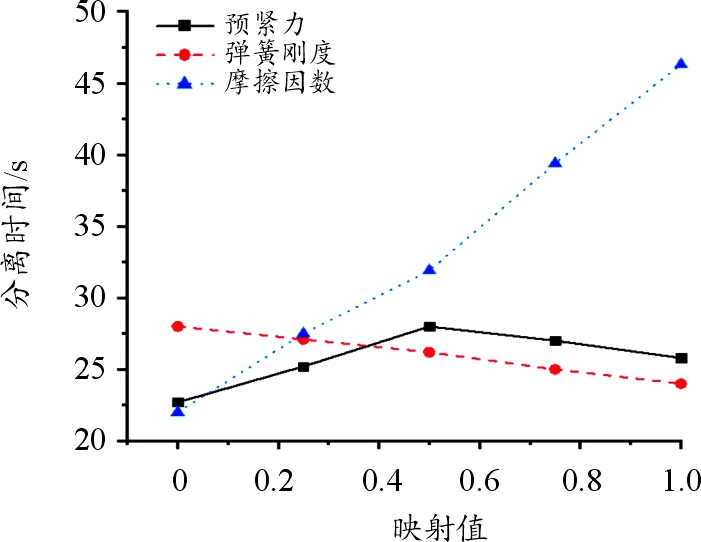
图21 影响分离时间的各因素曲线
Fig.21 Curve of factors affecting separation time
如图22所示，各因素对动态包络的影响显著性按从大到小的次序为C-T接触面摩擦因数、螺栓预紧力、分离弹簧刚度。摩擦因数值增加0.2，最小包络距减小了6.8%，最大包络距减小了4.3%；预紧力增加4 kN，最小包络距增加了1.4%，最大包络距减小了3.9%；弹簧刚度增加40 N/mm，最小和最大包络距分别增加了0.4%和0.6%。
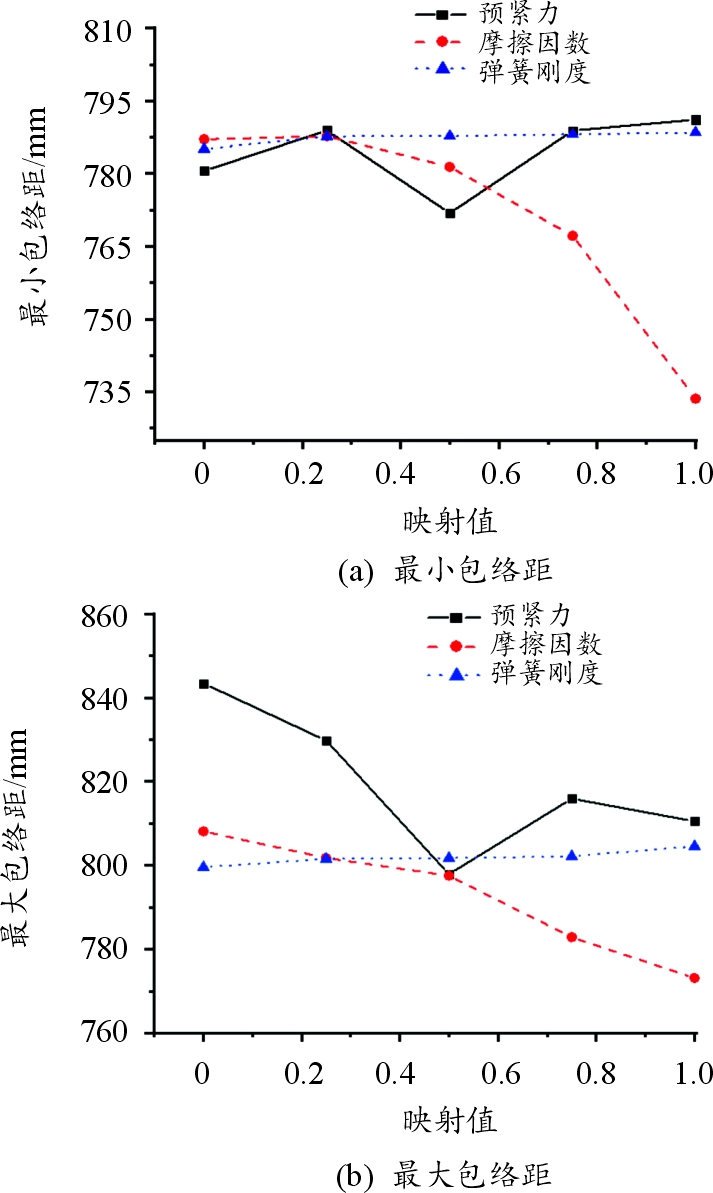
图22 影响包络距各因素曲线
Fig.22 Curve of factors affecting envelope distance
7 结论
1) 轴向接触载荷的理论计算结果和仿真结果的相对误差小于10%，验证了刚性包带有限元模型及其分析方法的有效性。
2) 根据仿真模型计算得出，刚性包带分离时间26.8 s，分离不同步时间22.7 s。动态包络呈两极稍扁、中间略鼓的椭圆形，最小和最大包络距分别为787.87 mm和802.15 mm。
3) 预紧力和摩擦因数的改变均会引起系统应变能和摩擦损耗能发生改变，进而影响包带分离性能。其中V型槽和V型缘接触面摩擦因数对分离时间和动态包络影响最为显著，摩擦因数由0.1增加到0.3，分离时间延长24.3 s，最小包络距减小6.8%，最大包络距减小4.3%。
[1] 宋美茜.有效载荷分离安全性及包络分析[D].哈尔滨：哈尔滨工业大学，2016.
Song M Q.Safety and envelope analysis of payload separation[D].Harbin:Harbin Institute of Technology，2016.
[2] 孙海霞，范瑞祥.星箭包带锁紧机构分离过程动态包络的动力学仿真[J].导弹与航天运载技术，2004(04):15-18.
Sun H X，Fan R X.The dynamic envelope simulation of the clamp band separation process[J].Missiles and Space Vehicles，2004(04):15-18.
[3] 秦朝烨，褚福磊,阎绍泽.包带式星箭连接结构轴向刚度研究[J].宇航学报，2009，30(05):2080-2085.
Qin Z Y，Chu F L，Yan S Z.Axial stiffness analysis of clamp band system[J].Journal of Astronautics，2009，30(05):2080-2085.
[4] 袁家军.卫星结构设计与分析(下)[M].北京：宇航出版社，2004.
Yuan J J.Design and analysis of satellite structures(volume 2)[M].Beijing:China Aerospace Publishing House，2004.
[5] 李恒.考虑空间热环境的星箭包带式连接结构力学特性研究[D].北京：中国地质大学，2016.
Li H.Studies on mechanical characteristics of clamp band joint under space thermal environment[D].Beijing:China University of Geosciences，2016.
[6] Qin Z Y，Yan S Z，Chu F L.Dynamic analysis of clamp band joint system subjected to axial vibration[J].Journal of Sound & Vibration,2010，329(21):4486-4500.
[7] Qin Z Y，Yan S Z，Chu F L.Finite element analysis of the clamp band joint[J].Applied Mathematical Modelling，2012，36(1):p.463-477.
[8] Barrans S M，Khodabakhshi G，Xu Q.Contact Pressure Distribution in Joints Formed by V-Band Clamps[J].Advanced Materials Research，2014，1016:34-38.
[9] Lancho M，Larrauri J V.Gómez-Molinero.CRSS:A separation system for launching very heavy payloads[J].Acta Astronautica,2000，47(2):153-162.
[10]于兵，张乔飞，唐科，张志峰等.一种低冲击、小包络、整环式有效载荷分离机构[P].中国专利：109798809，2019-05-24.
Yu B，Zhang Q F，Tang K，et al.A low impact，small envelope and integral ring payload separation device[P].China:109798809，2019-05-24.
[11]王林刚,梁言,龙连春.刚性包带关键参数对其分离性能的影响分析及包带结构设计优化[C]//中国力学大会论文集(CCTAM 2019).中国力学学会、浙江大学.杭州:2019:8.
Wang L G，Liang Y，Long L C.Influence analysis of key parameters of rigid cladding on its separation performance and optimization of cladding structure design[A].Proceedings of China mechanics Conference(CCTAM 2019)[C]//Chinese Society of Theoretical and Applied Mechanics、Zhejiang University.Hangzhou:2019:8.
[12]白绍竣.包带连接建模与力学特性研究[D].哈尔滨：哈尔滨工业大学，2010.
Bai S J.Studies into modeling and mechanic properties of marmanclampband joint[D].Harbin:Harbin Institute of Technology，2010.
[13]袁家军.卫星结构设计与分析(上)[M].北京：宇航出版社，2004.
Yuan J J.Design and analysis of satellite structures(volume 1)[M].Beijing:China Aerospace Publishing House，2004.