活性复合动能杆对混凝土靶侵爆效应研究
1 引言
海湾战争后，重要战略军事目标的坚固化、地下化，使得世界各国纷纷开始发展钻地武器，随着防护技术日益先进和复杂，常规钻地武器仅依靠单一动能侵彻毁伤难以满足作战需求。由铝颗粒填充的聚四氟乙烯(PTFE/Al)复合材料是一种典型的冲击反应活性材料，由于活性材料在强冲击作用下会迅速发生剧烈化学反应，能通过侵彻和爆炸双重毁伤机理的联合作用实现对目标的高效毁伤[1-3]。众多学者对PTFE/Al材料的制备工艺、冲击释能特性、粒径配比影响以及应用等方面研究较多[4-9]，而研究活性材料对混凝土侵爆毁伤效应的公开文献较少。曹辰等[10]采用SPH数值模拟方法，分析了侵爆战斗部着速和装药长径比对混凝土靶毁伤效应的影响；郭俊等[11]开展了活性分段动能杆对混凝土毁伤效应的实验，依据实验数据采用数值模拟方法探讨了活性分段动能杆惰性前级、活性动能杆结构及质量分数对混凝土靶的毁伤规律。
随着无网格法的兴起，其中物质点法(MPM)发挥了拉格朗日方法和欧拉方法各自的优点，适合应用于超高速碰撞、冲击侵彻、爆炸、滑坡等一系列涉及材料特大变形的问题[12-13]。王晓军等[14]将JH-2、HJC和RHT本构模型引入到物质点法，模拟了陶瓷和混凝土的冲击问题；邹家强等[15]应用物质点法对椭圆骨料混凝土进行数值模拟研究，建立的模型可较好地表征混凝土细观结构的各相信息。
活性复合动能杆由惰性动能杆、活性动能杆串联而成，惰性动能杆采用高强度金属先侵入目标一定深度，活性动能杆沿之前开孔随进，在侵爆耦合作用下对目标内部造成结构性破坏，扩大毁伤范围，并有效降低目标强度，提高了后续惰性杆的侵彻效率。本文针对活性复合动能杆对混凝土靶的侵爆效应进行了研究，首先开展了活性复合动能杆侵彻混凝土靶实验；在实验基础上，采用物质点法开源程序MPM3D-F90[16]，嵌入描述混凝土材料的RHT本构方程[17]及P-α状态方程[18]和描述活性材料的Lee-Tarver状态方程[19]，建立有效的数值计算模型，得到活性复合动能杆对混凝土靶的毁伤过程，通过对比PTFE/Al和PTFE对混凝土靶的毁伤效能，验证活性材料侵爆耦合作用对混凝土的高效毁伤。
2 实验方案
2.1 动能杆制备
实验共制备了2种动能杆：① 活性动能杆有1 mm外壳，由45#钢制成，内核材料为PTFE/Al，采用模压烧结成型法制备满足零氧平衡组分的活性材料，活性试件制备流程如图1所示；② 惰性动能杆无外壳，由钨合金材料制成。
2种动能杆长径比均为2∶1，质量约为8.5 g，2种动能杆尺寸与实物如图2所示。
图1 活性材料制备流程框图
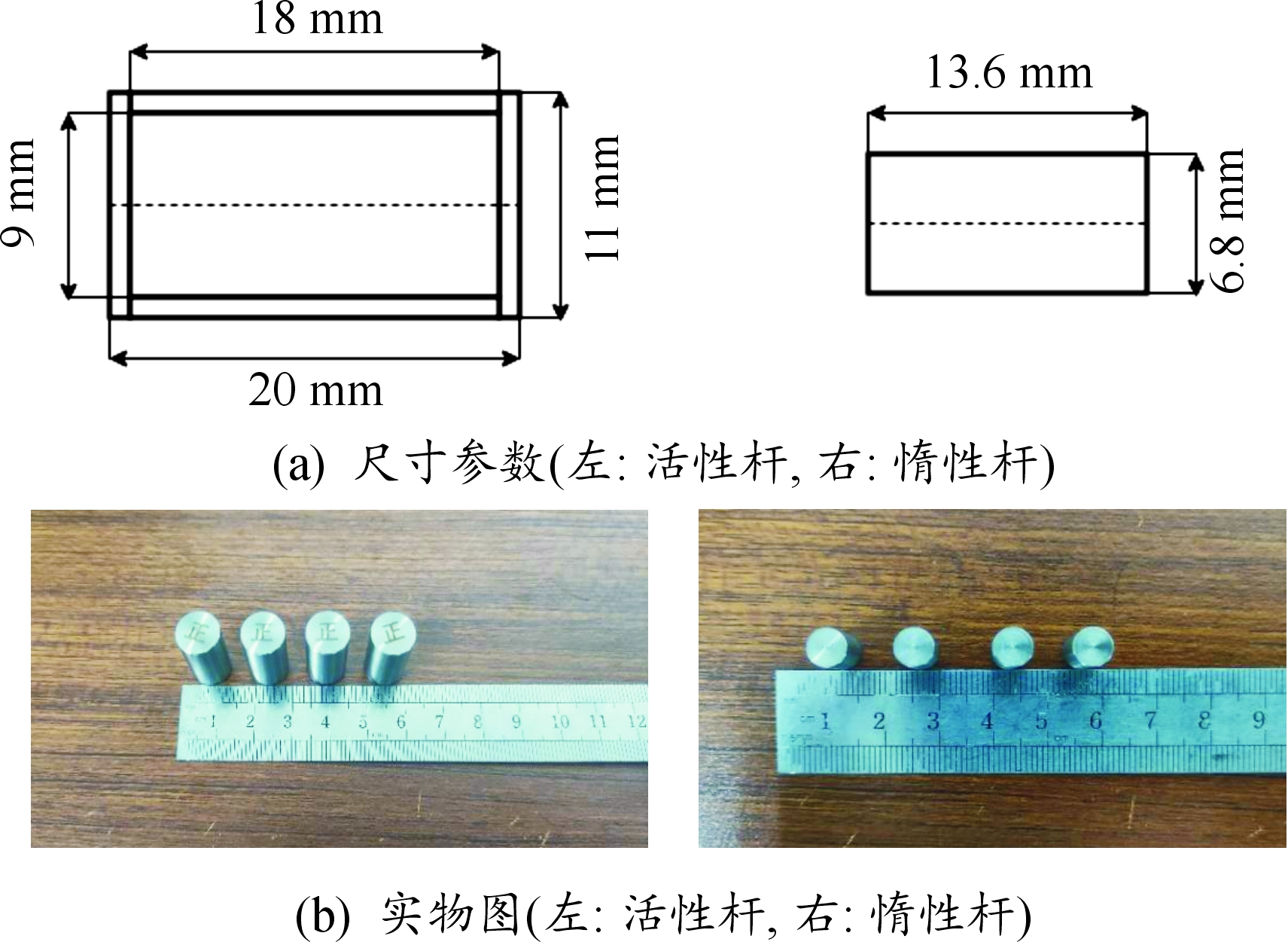
图2 动能杆尺寸设计及实物图
2.2 混凝土靶
混凝土靶采用浇筑成型的方法，经养护后单轴抗压强度为40 MPa，外层钢壳采用45#钢，混凝土靶尺寸与实物如图3所示。
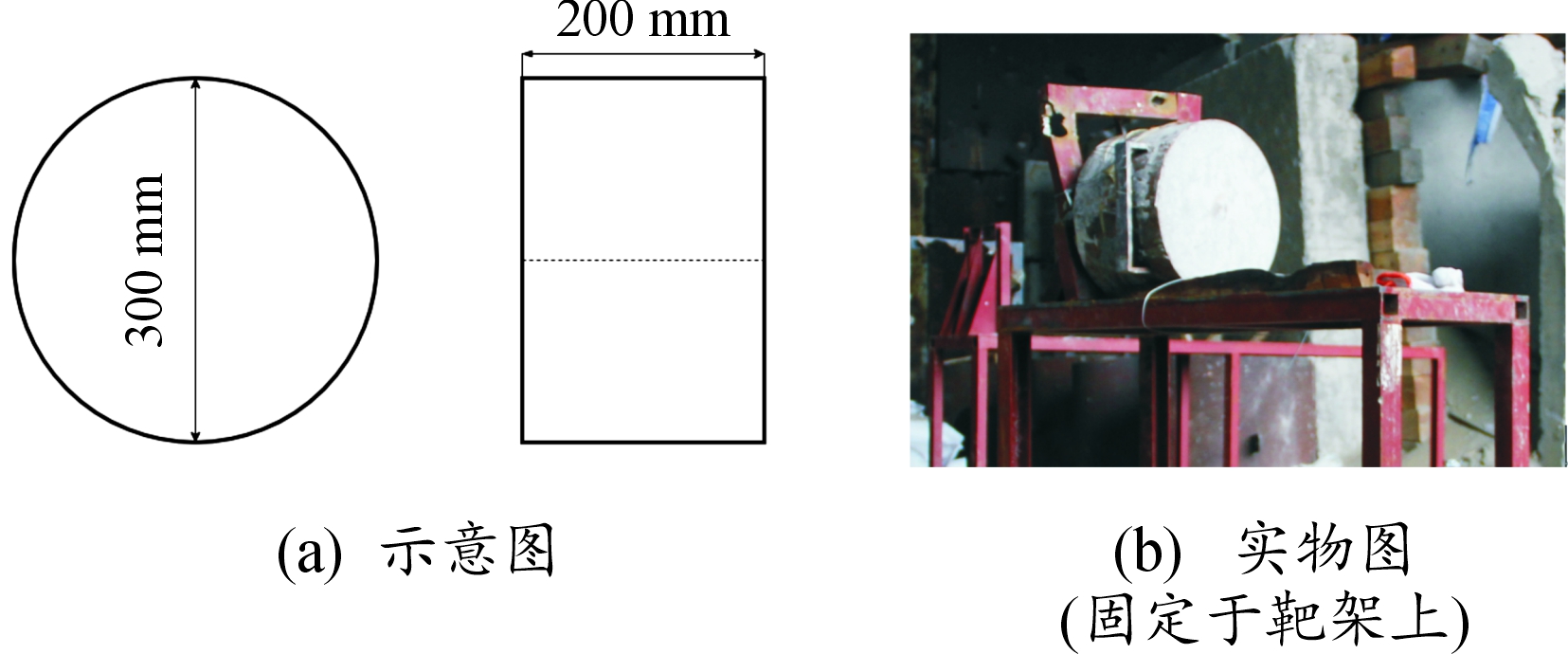
图3 混凝土靶示意图及实物图
2.3 实验系统
图4为本次实验设计场景示意图。实验采用发射药驱动的25 mm口径弹道炮作为加载平台，通过调节发射药筒装药量来控制动能杆初速为1 800 m/s以上；测速装置为双层铝箔纸，并利用高速摄影仪记录动能杆飞行姿态及终点毁伤效应；依次发射惰性动能杆和活性动能杆，通过测量动能杆侵彻深度分析活性复合动能杆对混凝土靶的侵爆效应。实验现场布置如图5所示。
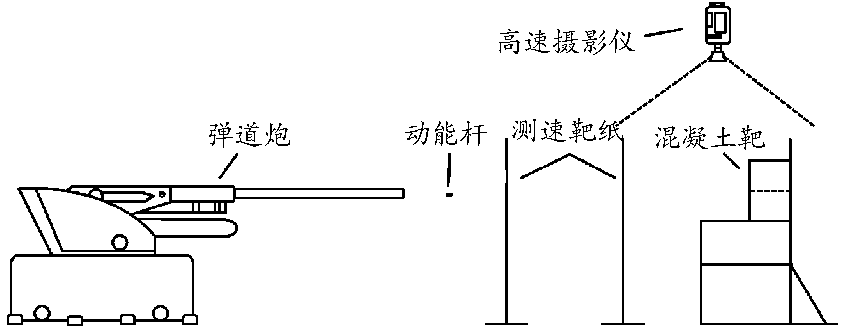
图4 实验设计场景示意图
图5 实验现场布置图
3 实验结果
3.1 高速摄影记录
图6给出了第一组实验中每发动能杆侵彻混凝土靶的高速摄影图像，由于阴雨天气下光线较弱，高速摄影仪不能很好地捕捉弹体的飞行姿态，这里只给出了弹体撞靶后的侵彻过程。
图6 高速摄影记录侵彻过程图像
从图像可以看出，惰性杆只在与靶体碰撞的初始时刻有闪光现象(图像中其他时刻的闪光现象是分离后的弹托与靶架撞击产生)，这是惰性金属与混凝土骨料颗粒碰撞伴随着剧烈摩擦引起的；而活性动能杆侵彻过程中不只有金属壳体与混凝土碰撞产生的闪光，还有活性内核受到挤压发生燃烧、爆炸化学反应出现的发光放热现象。
3.2 毁伤形貌
共进行了3组实验，实验结果如表1所示，图7～图9为每发弹体侵彻的最终形貌图。
表1 实验结果
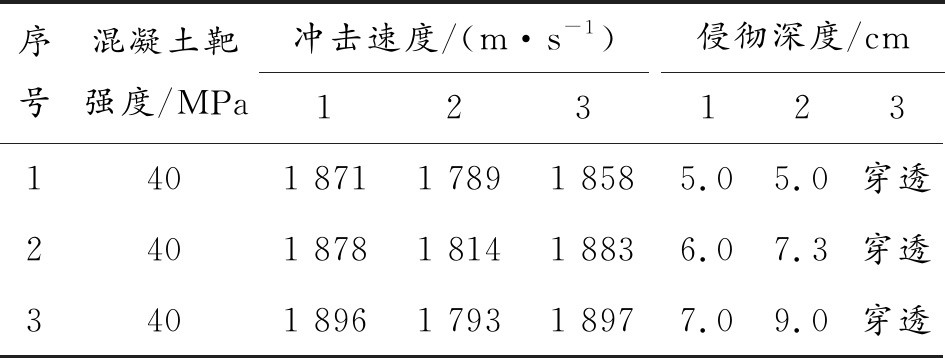
由图7可以看出，第1发钨合金动能杆撞击靶体后，在混凝土靶表面形成了明显的锥形凹坑，侵彻深度在5～7 cm；第2发活性动能杆撞击混凝土靶后，侵彻深度增加不是特别明显，由图8可以看出，活性动能杆撞击过程中发生反应造成混凝土靶表面剥落，破坏面积增大；第3发钨合金动能杆侵彻后完成了对混凝土靶的穿透，靶体背部产生明显的裂纹(如图9(c)所示)。可以推出：经活性动能杆对混凝土靶侵彻后，靶体内部受到较大损伤，材料强度有所降低，钨合金动能杆的侵彻深度明显增加。
图7 第1发钨合金杆侵彻混凝土靶后毁伤情况
图8 第2发活性杆侵彻混凝土靶后毁伤情况
图9 第3发钨合金杆侵彻混凝土靶后毁伤情况
4 数值模拟与结果分析
4.1 物质点法简介
基于更新拉格朗日格式，连续体运动的动量方程为:
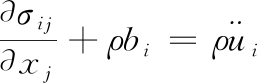
(1)
式(1)中：σij为柯西应力；xj为当前连续体在空间中的坐标；ρ为当前密度；bi为体力；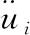
为加速度。
物质点法将连续体数值离散化为一系列物质点，每个物质点携带了密度、速度和应力等各种物理量。由于每个物质点携带的质量固定，自然满足质量方程。采用物质点离散，连续体的密度可近似表示为：
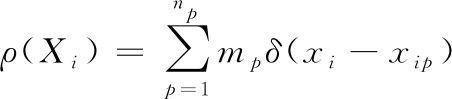
(2)
式(2)中：np为物质点总数；mp为每个物质点的质量；δ(x)为Dirac delta函数；xip为空间上物质点的坐标。
求解动量方程时，物质点与背景网格固连，通过建立背景网格结点有限元形函数NI(xj)，来实现物质点和背景网格之间的信息映射关系。带下标I、J的量表示网格结点变量，带下标p的量表示质点携带的物理量信息，质点与结点映射关系可表示为：
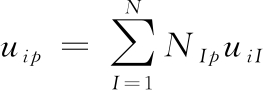
(3)
式(3)中：N为背景网格结点总数；NIp为结点I的形函数在质点p的值；uiI为结点I在i方向的位移。
动量方程可以表示为：
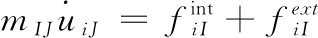
(4)
式(4)中，结点质量、内力和外力可以表示如下：
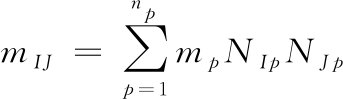
(5)
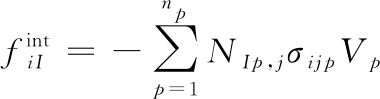
(6)
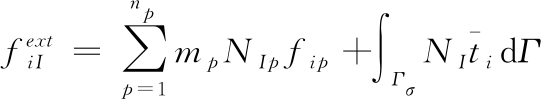
(7)
式(5)～(7)中：NIp,j=NI,j(xp)；σijp为质点p的应力；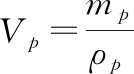
为质点p的体积；Γσ为面力边界；
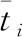为相应的给定面力。
利用中心差分法对式(4)进行积分，得到下一个时间步的动量后，再通过建立在背景网格上的形函数，得到物质点上的物理量计算应变和应力。在下一个时间步，抛弃变形后的背景网格，仍使用初始时规则的背景网格，这样既避免了网格畸变带来的困难，又可避免因对流项造成数值耗散而导致计算效率降低的问题。因此特别适合于分析超高速碰撞、冲击侵彻、爆炸、材料破坏等一系列涉及材料特大变形的问题。
4.2 材料模型与参数
采用物质点法建立活性复合动能杆侵彻混凝土靶的数值计算模型，表2为数值模拟中各材料所用的本构方程及状态方程。
表2 各材料所用的本构方程及状态方程
Lee-Tarver状态方程采用点火、增长两项式描述反应速率，该模型的反应速率为：
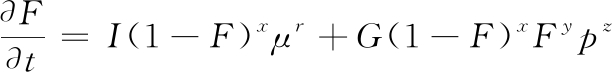
(8)
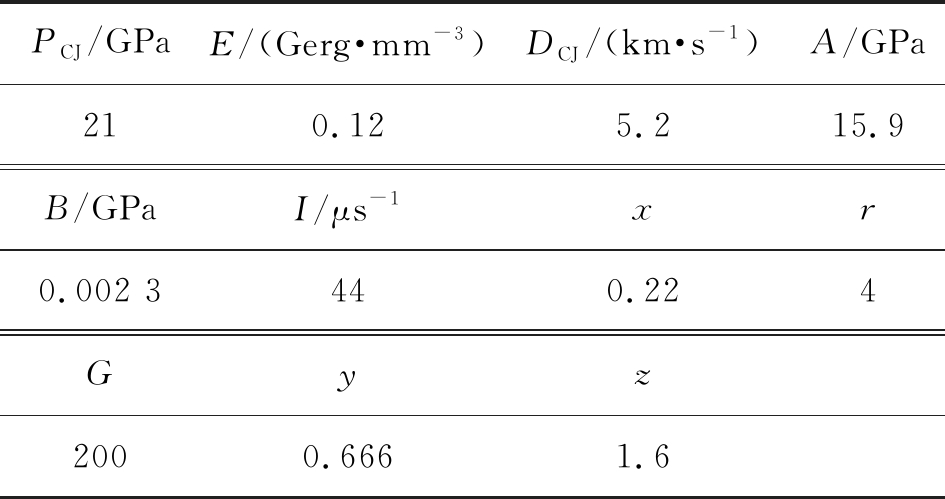
式(8)中：F为反应速率；p为炸药中的压力；I、x、r、G、y和z为材料相关常数；μ为压缩系数。
μ表示为：
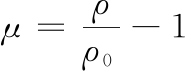
(9)
当压缩系数μ大于C-J压缩系数μCJ时，反应速率F=1，μCJ表达式为：
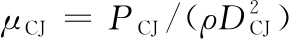
(10)
式(10)中：PCJ为C-J压力；DCJ为C-J爆速。
表3给出了Lee-Tarver状态方程相关参数。
表3 Lee-Tarver状态方程参数
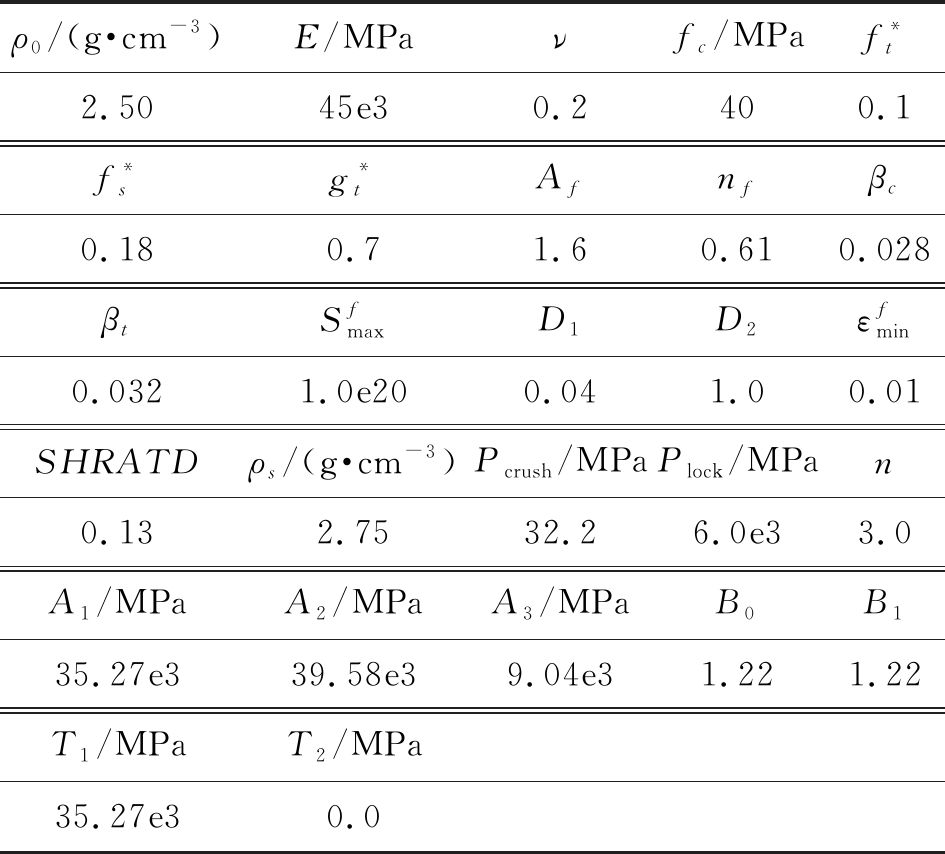
数值计算所使用的混凝土RHT模型和P-α状态方程材料参数如表4所示。
表4 混凝土材料参数
4.3 活性复合动能杆侵彻算例
考虑到对称性，建立1/4模型进行计算。离散时，物质点间距为1 mm，背景网格间距为2 mm，粒子总数约为87万。第1发钨合金杆仿真计算典型时刻如图10所示。
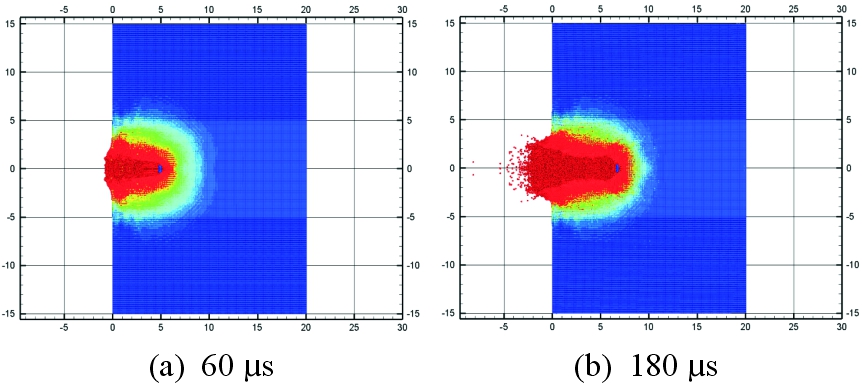
图10 第1发钨合金杆仿真计算典型时刻图
实验中每发动能杆是依次发射的，为了使数值计算更贴合实验工况，需要在每发动能杆侵彻完成后，将下一发动能杆初始位置周边失效物质点删除以防发生穿透，再导出混凝土各状态参量,并添加新的弹体模型形成重启动文件继续计算。照上所述，第2发活性杆仿真计算典型时刻如图11所示。
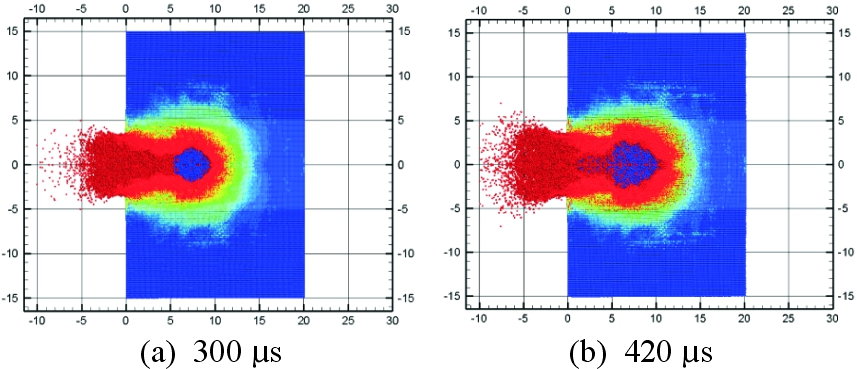
图11 第2发活性杆仿真典型时刻图
采取与第2发活性杆相同的计算形式，得到第3发钨合金杆仿真计算典型时刻如图12所示。
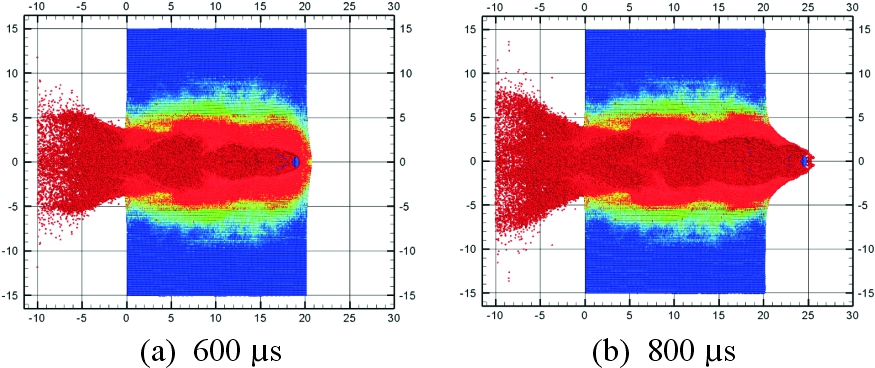
图12 第3发钨合金杆仿真计算典型时刻图
为验证PTFE/Al材料对混凝土的侵爆毁伤效应，将第2发活性杆换为相同密度的PTFE杆，得到PTFE杆对混凝土造成的毁伤形貌如图13所示。
图13 PTFE杆仿真计算典型时刻图
4.4 仿真结果分析
可以看出，数值计算模型得到的结果与实验吻合较好。其中第2发活性杆侵彻深度偏高，这是因为实验过程中第1发钨合金杆终点孔径较小，由于发射精度受限难以保证前后2发动能杆的着靶点相同，而在仿真计算中活性杆是循第1发造成的穿孔继续侵彻，得到的结果是偏理想化的。
图14、图15分别为PTFE/Al和PTFE侵彻后混凝土完全损伤区域。经测量，PFFE/Al完全损伤域宽度达5.4 cm，深度可达14.3 cm；PTFE完全损伤域宽度为4.9 cm，深度为13.7 cm；PTFE/Al的完全损伤区域比PTFE高出33%。
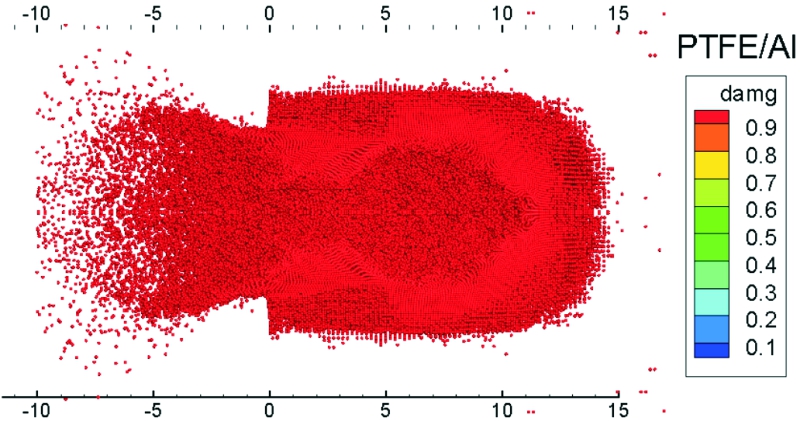
图14 PTFE/Al材料的完全损伤区域仿真图
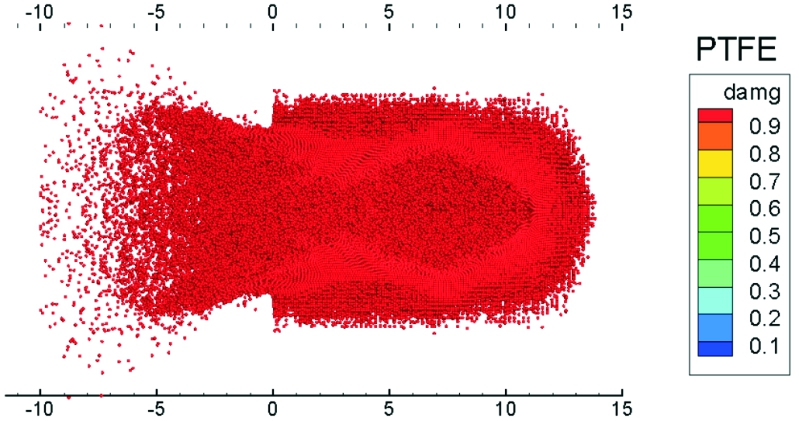
图15 PTFE材料的完全损伤区域仿真图
对PTFE/Al杆和PTFE杆形成孔洞后方混凝土的压力进行观测，图16、图17分别为活性杆和PTFE杆侵彻过程中各位置处的压力时程曲线。由图16、图17可知,活性材料发生反应后应力波迅速传播，到达观测位置后，压力在瞬间达到峰值，然后逐渐衰减。由于爆轰波传播到边界发生反射，会出现峰值较小的负压。
图16 活性杆各位置压力时程曲线
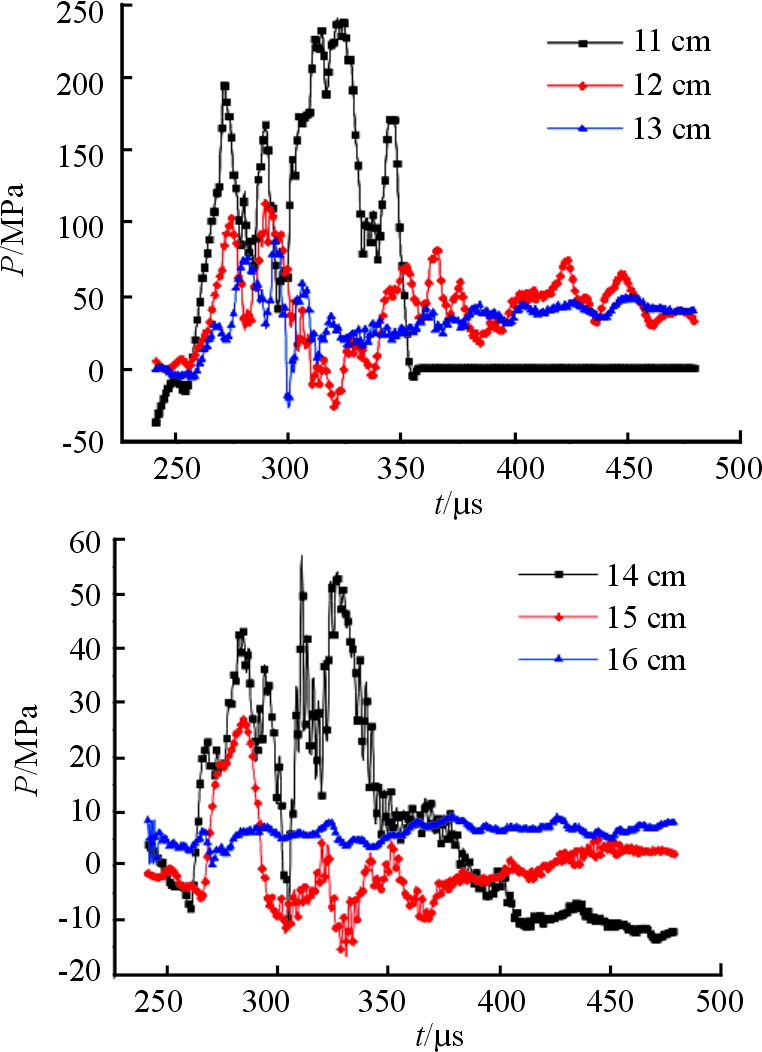
图17 PTFE杆各位置压力时程曲线
随着距离的增加，观测位置处的峰值压力逐渐减小，图18给出了2种材料的压力峰值衰减曲线，从图18中可以看出，在任意位置处PTFE/Al材料的峰值压力都是大于PTFE材料的，距离较近时，PTFE/Al的峰值压力要远高于PTFE，11 cm处PTFE/Al的峰值压力为323 MPa，PTFE的峰值压力只有240 MPa；随着应力波衰减，16 cm处PTFE/Al的峰值压力降为24 MPa，PTFE已经降为8 MPa。
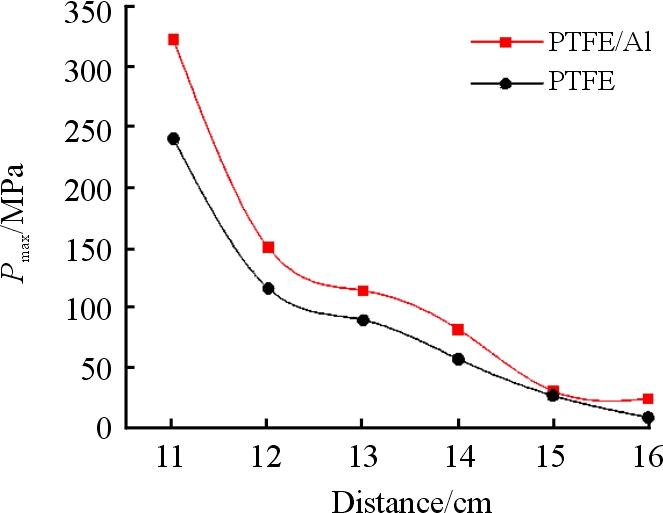
图18 压力峰值衰减曲线
通过上述分析，可以得出活性材料对混凝土造成的冲击更强、破坏面积更大、预损伤范围更广，同时体现了活性材料的动能侵彻和爆炸耦合作用是一种高效的毁伤模式。
5 结论
1) 基于25 mm口径弹道炮发射平台进行了活性复合动能杆对混凝土靶的毁伤效应研究，实验结果表明活性杆的侵彻深度虽然较低，但其侵爆效应能增大混凝土破坏面积，通过对混凝土内部结构造成预损伤降低了靶体强度，大大提高了钨合金杆的侵彻效率。
2) 将物质点法应用于活性复合动能杆侵彻混凝土的数值模拟之中，建立的模型计算结果与实验数据吻合较好，解决了拉格朗日方法在处理大变形问题上网格畸变的缺陷，是一种研究活性材料侵爆效应问题新的有效方法。
3) 对比PTFE/Al杆和PTFE杆对混凝土造成的完全损伤域，活性材料比惰性材料高33%，活性材料的预损伤范围更广；通过压力峰值衰减曲线得到活性材料对混凝土的冲击强度明显大于惰性材料，体现了活性材料侵爆耦合作用的高效性。
[1] Grudza M E，Jann D，Forsyth C，et al.Explosive launch studies for reactive material fragments[C]//Proc.of the 4th Joint Classified BombaAvarhead and Ballistics Symposium.Newport，2001:110-118.
[2] Myriski B.Shear-driven ractive material combustion at high-speed impact[C]//Proc.of the 2005 Joint Classsified Warheads and Ballistics Symposium，Colorado，America，2005.
[3] 王海福,刘宗伟,俞为民,等.活性破片能量输出特性实验研究[J].北京理工大学报，2009，29(08):663-666.
[4] Nielson D B，Tanner R L，Lund G K.High strength reactive materials and methods of making，US,7307117[P].2007-12-11.
[5] MOCK W，HOLT W H.Impact initiation of rods of pressed polytetrafluoroethylene(PTFE) and aluminum powders[C]//Proc.of the AIP Conference Proceedings.American Institute of Physics，2006.
[6] 李尉,任会兰,宁建国,等.Al/PTFE 活性材料的动态力学行为和撞击点火特性[J].含能材料,2020,28(01):38-45.
[7] Mock W，Drotar J T.Effect of aluminum particle size on the impact initiation of pressed PTFE/Al composite rods[J].Shock Compression of Condensed Matter，2007，955:971-974.
[8] 胡万翔，毛亮，姜春兰，等．Al粒径对PTFE/Al活性材料动态力学性能的影响[J]．兵器装备工程学报，2020， 41(05):183-187．
[9] Raftenberg M N,Mock W，Kirby G C.Modeling the impact deformation of rods of a pressed PTFE/Al composite mixture[J].International Journal of Impact Engineering，2008，35(12):1735-1744.
[10]曹辰，肖建光，汪秀明,等.侵爆战斗部作用混凝土靶毁伤效应[C]//第六届全国强动载效应及防护学术会议暨2014年复杂介质/结构的动态力学行为创新研究群体学术研讨会论文集.北京：2014.
[11]郭俊.活性分段动能杆对混凝土靶的毁伤效应研究[D].北京：北京理工大学,2016.
[12]张雄，刘岩.物质点法[M].北京：清华大学出版社，2013.
[13]马上，张雄，邱信明.超高速碰撞问题的三维物质点法[J].爆炸与冲击，2006，26(03):273-278.
[14]王晓军.陶瓷和混凝土冲击问题的物质点法研究[D].北京：清华大学,2012.
[15]邹家强，张巍，刘爱华．物质点法在椭圆骨料混凝土损伤模拟中的应用[J]．人民长江，2019，50(07):174-178．
[16]张雄.冲击爆炸三维物质点法数值仿真软件(MPM3D)[P].CN:2009SRBJ4761.2009.7.
[17]Riedel W，Thoma K，Hiermaier S，et al.Penetration of reinforced concrete by beta-b-500 numerical analysis using a new macroscopic concrete model for hydrocodes[C]//Proc.of the 9thInternational Symposium，Interaction of the Effects of Munitions with Structures，1999.
[18]Herrmann W.Constitutive equation for the dynamic compaction of ductile porous materials[J].Journal of Applied Physics,1969，40(06):2490-2499.
[19]Lee E L,Tarver C M.Phenomenological model of shock initiation in heterogeneous explosives[J].Physics of Fluids，1980,23(12):2362-2372.