初始不均衡量对潜艇悬停操纵的影响
1 引言
潜艇在战斗活动中，为了隐蔽待机、消除动力器材工作噪音以及为了节省电能或冷却蓄电池，而又无合适海底潜坐时，可以选择在安全深度和工作深度范围内进行停车悬停。潜艇水下悬停具有重要的战术意义[1]，潜艇采取悬停操纵方法，不但可以减少电能消耗、延长阵地待机时间，更是降低潜艇噪声，增大声纳发现距离的最有效方法。目前，部分学者对潜艇悬停的运动模型建立和自动悬停控制方法进行了研究。其中，应东对潜艇水下悬停运动进行了建模分析，研究了不同因素对悬停操纵的影响[2]；俞科云等分析了悬停运动的特征，并对潜艇水下悬停运动的控制进行了仿真研究[3]；郝英泽等分析了海水密度变化对潜艇悬停垂向运动的影响，得出了稳定深度与海水密度变化率的量的关系[4]；熊瑛等针对潜艇水下悬停控制设计了一种模糊控制器，通过仿真表明模糊控制器具有超调量小、调整时间段及鲁棒性好的特点[5]。潜艇进入悬停战术机动前，需要进行准确均衡使潜艇的浮力差和力矩差尽量接近零以利于即将进行的悬停操纵。然而由于受限于艇员的操纵训练水平和操艇装备的技术条件限制，潜艇在进入悬停之前完全消除浮力差和力矩差是不现实的。基于此，本文通过分析悬停运动的操纵方法和进入悬停阶段前产生初始不均衡量的原因，进而以模型潜艇为研究对象，在潜艇悬停运动数学模型的基础上进行仿真计算，研究进入悬停机动前的剩余浮力差、剩余力矩差和初始垂速对潜艇悬停操纵的影响。在仿真结果的基础上，分析了初始不均衡量和悬停稳定性之间的逻辑关系。
2 潜艇水下悬停运动的操纵
2.1 悬停运动的4个阶段
潜艇水下悬停操纵可以大致分为4个阶段：
1) 悬停准备阶段。在进入悬停操纵战术机动之前，需要选择合适的悬停海域和悬停深度。阶梯型、海山型、海沟型的海底地貌，容易产生折射流、反射流等不规则的紊乱流场，使潜艇悬停深度不易控制，因此，应选择海底地貌平坦的海区进行悬停。
2) 进入悬停阶段
进入悬停阶段从停车、补充均衡开始，至潜艇稳定于指令悬停深度。本阶段的操纵控制目标是：尽量消除初始不均衡力(矩)，同时控制潜艇垂速尽量接近零，尽快使潜艇进入悬停的稳定深度状态。
3) 保持悬停深度阶段。在这一阶段，通过悬停系统的注排水和艏艉均衡水舱的调水消除引起选悬停深度波动的浮力差及力矩差，使潜艇稳定的保持在目标深度上。在悬停过程中，可能造成潜艇悬停深度波动的主要干扰包括初始不均衡量，海水密度变化以及艇体压缩变化。此外，悬停水域的水文情况、流速流向，尤其是对悬停过程中补充均衡的时机选择，指挥员对本艇零航速潜浮惯性运动特性的认识和掌控，是实现稳定潜艇悬停的关键。
4) 退出悬停阶段。潜艇从悬停状态可直接转入机动航行，并辅以补充均衡即可。有敌情顾虑的情况下，应低速转入机动并采取向浮力调整水舱注、排水和调水措施，操纵潜艇以较大纵倾和垂速迅速驶入有利隐蔽的作战深度。
2.2 进入悬停前的初始不均衡量
由于潜艇上下不对称导致存在零升力和零升力矩，并且零升力(矩)的大小与航速的平方成正比[6]。因此在潜艇由有航速状态逐渐进入悬停状态时，随着航速的不断减小，零升力(矩)逐渐消失，因此会出现艇重，并出现力矩差。为了保持潜艇无纵倾定深悬停，就必须进行准确补充均衡。
在潜艇逐渐降速至零航速状态过程中，按零升力和零升力矩公式计算浮力差的变化量为：
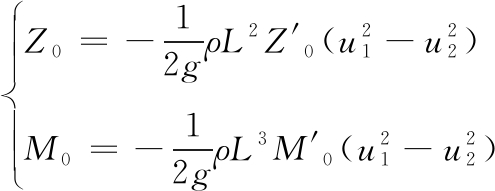
(1)
式中：Z0、M0为潜艇减速至零航速而减小的零升力和零升力矩；u1为停车航速；u2为悬停航速，即u2=0。
停车后均衡量可按下述公式进行计算：
(2)
式中：xv为浮力调整水舱容积中心到潜艇重心的纵坐标；Lvbs为艏艉纵倾平衡水舱容积中心之间的纵向距离。
所谓初始不均衡量，是指潜艇进入悬停前的实际浮力差和力矩差。当潜艇进行悬停机动时，要求潜艇要准确均衡，以保证潜艇的浮力差和力矩差都为零，但在实际悬停过程中很难做到这一点。一般来说，潜艇停车时航速的大小、均衡精度以及可能的人为误差是影响初始不均衡量的主要因素。
3 悬停操纵运动控制数学模型
3.1 悬停运动基本数学模型
据潜艇垂直面运动规律，水下悬停类似于潜艇在垂直面的惯性潜浮运动，因此，由潜艇垂直面操纵运动非线性方程式[7]，经过合理简化后，潜艇水下悬停运动的基本数学模型为：
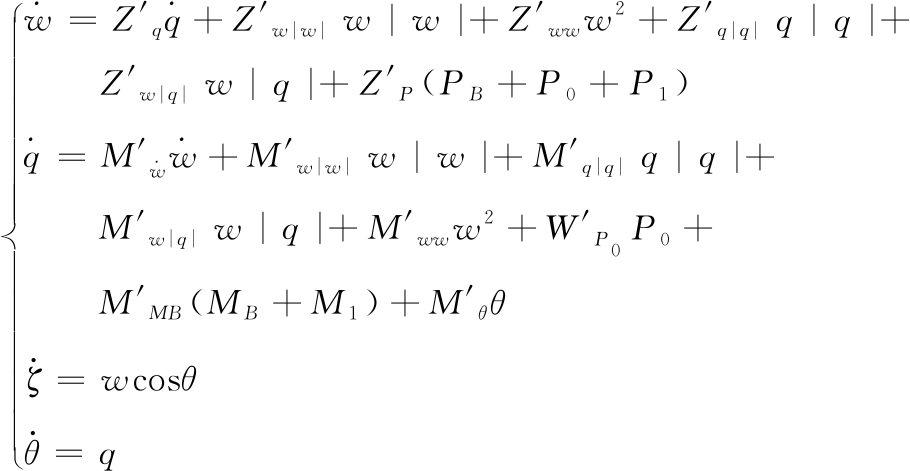
(3)
式中：u、w分别是纵向速度、垂向速度；θ、q分别是纵倾角、纵倾角速度、纵倾角加速度；PB为剩余浮力，由三部分组成，包括初始不均衡量、艇体压缩产生的力和海水密度变化引起的力；P0为主动控制力，即由悬停水舱注排水产生的控制力；P1为外干扰力；MB为剩余浮力力矩，包括初始不平衡力矩和均衡系统产生的力矩；M1为外干扰力矩。其余带下标的参数为潜艇的水动力系数[8]。
3.2 海洋环境干扰力模型
海洋环境对潜艇悬停的影响是非常复杂的[9]，为方便研究，对干扰力模型进行了一定的简化是必要的。由于海水的温度、盐度对潜艇悬停的影响是通过海水密度的变化反映出来的，同时海水压力对潜艇悬停的影响是通过艇体压缩反映出来的，本研究将干扰力模型统一为艇体压缩模型和海水密度变化模型[10-12]。
1) 艇体压缩模型
艇体压缩量随深度增加而变化设为0.029 t/m，艇体压缩产生的力按式(2)计算：
P3=0.029(ζ-ζ0)
(4)
式中：ζ为潜艇当前深度；ζ0为潜艇初始深度。
2) 海水密度变化模型
各深度下海水密度变化产生的力按式(3)计算:
P4=-V(ρ-ρ0)
(5)
式中：V为潜艇水下全排水量；ρ为潜艇初始深度下的海水密度；ρ0为潜艇当前深度下的海水密度。
均匀层情况下取海水密度为一个定值，即认为海水密度不变化。
正梯度情况密度按照以下公式计算：
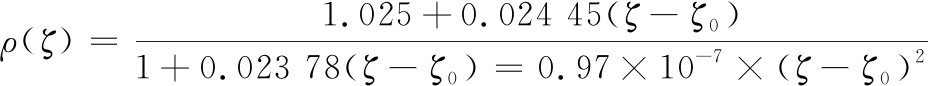
(6)
负梯度情况，密度变化公式为：
ρ(ζ)=1.025-0.000 01(ζ-ζ0)
(7)
式中： ρ(ζ)为当前深度下的海水密度； ζ为当前深度；ζ0为初始深度。
3.3 悬停水舱注排水控制模型
潜艇悬停时所用到的控制执行机构主要是悬停专用水舱。悬停水舱实际水量容积Q为考虑相应控制规律、水舱状态初始条件Q0和最大可能的注排水量Qmax后的水舱状态方程的积分结果[13-15]。
悬停专用水舱状态方程形式如下：
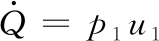
(8)
其中：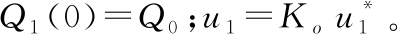
悬停水舱水量满足如下条件：
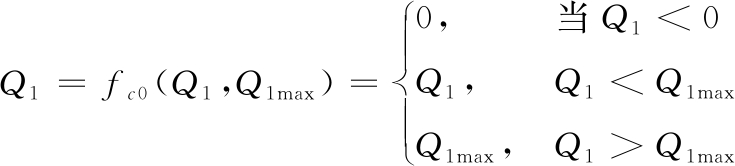
(9)
式中： u1为注排注水控制信号；p1为悬停水舱注排水速率；Q0为悬停水舱初始注水量；Ko为阀门开启系数。
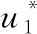由控制率计算，取值含义如下：
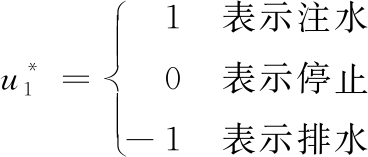
(10)
3.4 悬停水舱阀门开启模型
在初始状态水舱阀门是全关的，阀门开启系数Ko =0，在接收到注排水或调水控制信号后阀门在响应时间内按线性过程由全关变化到全开。
当在进行注排水时，水舱阀门是全开的，阀门开启系数Ko =1，在接收到停止注排水或调水控制信号后阀门在响应时间内按线性过程由全开变化到全关。
3.5 模型有效性分析
为了验证悬停操纵运动控制数学模型的有效性，对海水密度为负梯度条件下的潜艇悬停进行了仿真，仿真条件尽可能与模型潜艇操纵试验时的海洋环境接近。具体的仿真环境为：海水密度梯度类型为弱负梯度，梯度值-0.000 015，悬停稳定深度40 m，潜艇初始不均衡量0.5 t，悬停水舱注排水速率10 L/s。
表1 数学模型有效性比对
Table 1 Comparison of the validity of mathematical models
通过表1的分析对比数据可以看出，在相似海洋环境条件下，悬停仿真值与试验值非常接近，特别是单位时间的注排水次数几乎相等，单位时间注排水量的误差也不到3%。可以得出结论：本文采用的潜艇悬停运动数学模型能够较真实地反映潜艇的实际悬停操纵过程，从而验证了潜艇悬停运动数学模型的有效性。
4 初始不均衡量对水下悬停影响仿真分析
通过前面的分析可以知道，均衡计算误差的存在是不可避免的，因此，研究均衡计算误差也就是初始不均衡量对潜艇悬停的影响是很有必要的。一般来说，初始不均衡量又包括剩余浮力差和剩余力矩差。
海水比重垂直面变化梯度通常有3种典型的形式[4]：第1种是海水密度随深度增加而增大，即密度呈正梯度变化，如图1(a)所示；第2种是海水密度不随深度变化，即密度均匀层，如图1(b)所示；第3种是海水密度随深度的增加而减小，即密度呈负梯度变化，如图1(c)所示。3种典型形式中，负梯度类型对悬停系统的要求是最苛刻的，一艘潜艇如果能在负梯度类型的海水中成功，在均匀层和正梯度类型的海水中也一样能够准确悬停。因此本文的所有仿真均是在对悬停系统性能要求最为苛刻的负梯度类型条件下进行的。
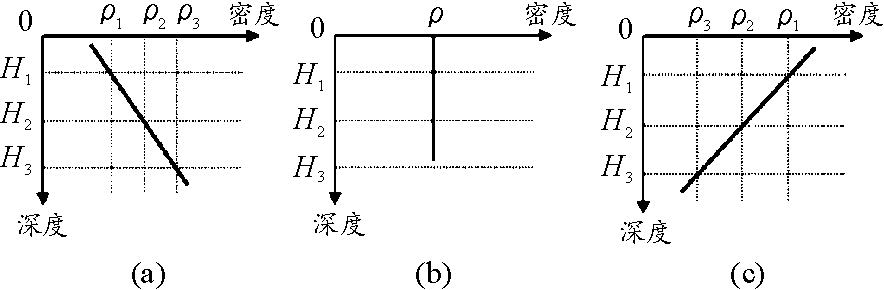
图 1 3种典型梯度类型示意图
Fig.1 Three typical gradient types
基于悬停运动基本数学模型、环境干扰力模型和悬停水舱注排水控制模型，以模型潜艇为研究对象，采用C#语言编写了潜艇水下悬停操纵运动仿真软件，进而通过悬停仿真进一步分析初始不均衡量对潜艇悬停操纵的影响。
4.1 剩余浮力差对悬停的影响
图2～图4分别为均衡计算误差为0.2 t、0.4 t、1.0 t时的悬停仿真结果。仿真图中4条曲线分别是深度、主动控制力、累计注排水量和累计注排水次数与悬停时间的关系。仿真条件设置：海水密度梯度值-0.000 01，悬停水舱注排水速率10 L/s，目标悬停深度100 m，悬停水舱阀门开启时间6 s。
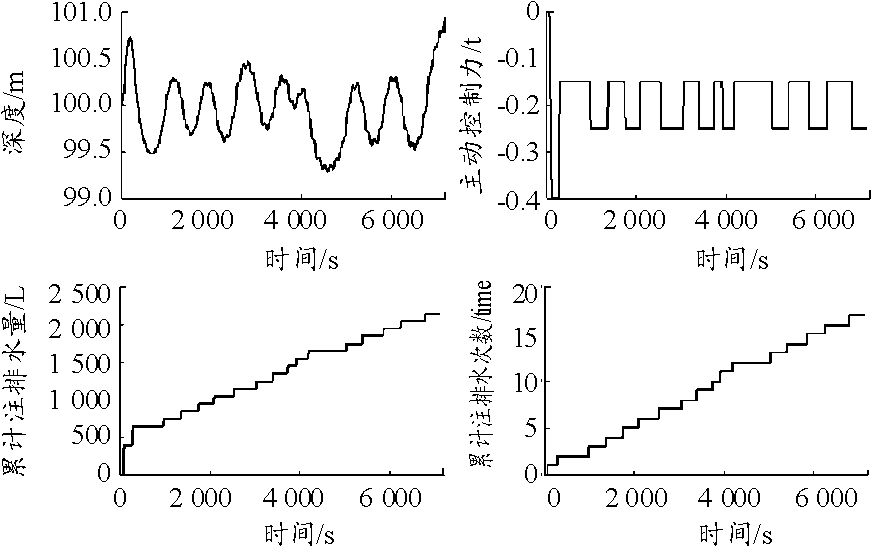
图2 剩余浮力差为0.2 t时的悬停仿真曲线
Fig.2 Residual buoyancy difference is 0.2 t
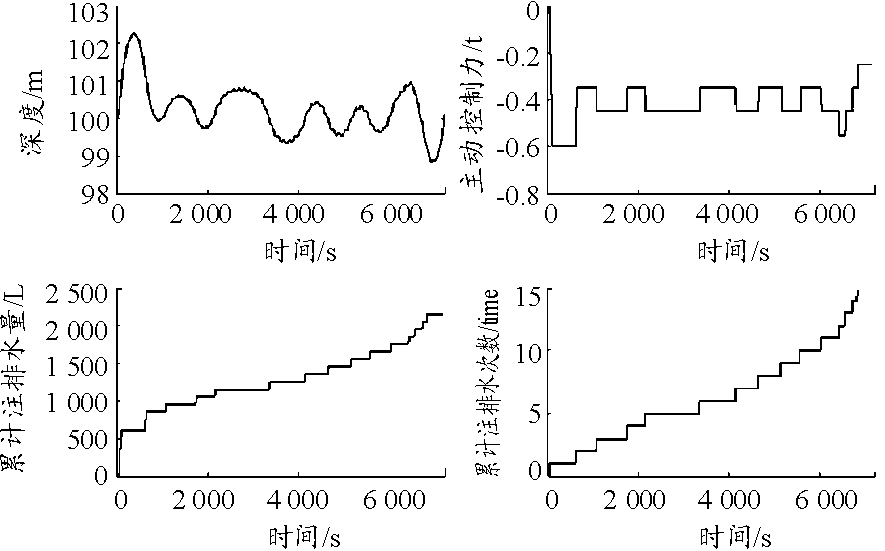
图3 剩余浮力差为0.4 t时的悬停仿真曲线
Fig.3 Residual buoyancy difference is 0.4 t
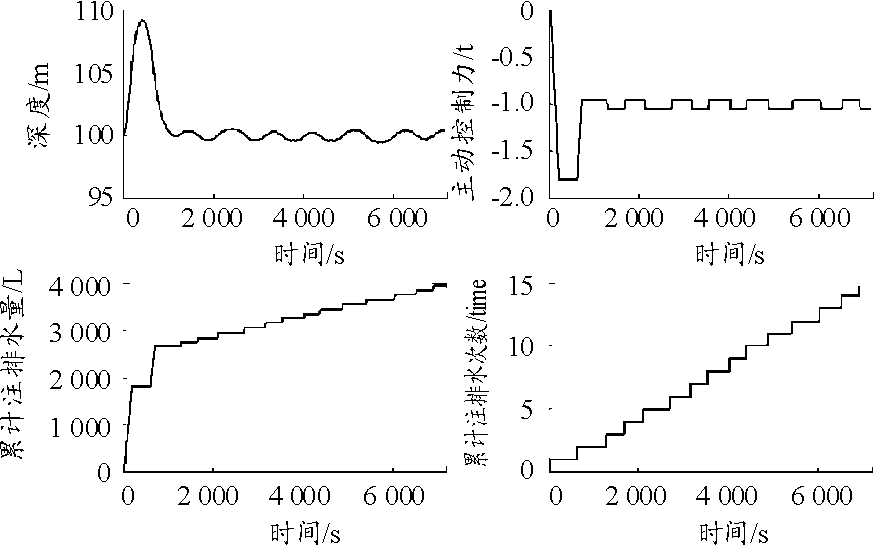
图4 剩余浮力差为0.8 t时的悬停仿真曲线
Fig.4 Residual buoyancy difference is 0.8 t
表2为海水密度梯度值-0.000 01，剩余浮力差对潜艇悬停影响的仿真结果。表2中最后三项数据分别为平均注排水量、平均注排水时间和平均注排水次数，而仿真图中为累计注排水量和累计注排水时间，二者是有区别的。表中的挽回深度定义为：当潜艇存在初始不均衡量时，经过一次注(或排)水，潜艇偏离初始深度的最大值。
表2 剩余浮力差对潜艇悬停参数的影响数据
Table 2 Influence of residual buoyancy difference on submarine hovering
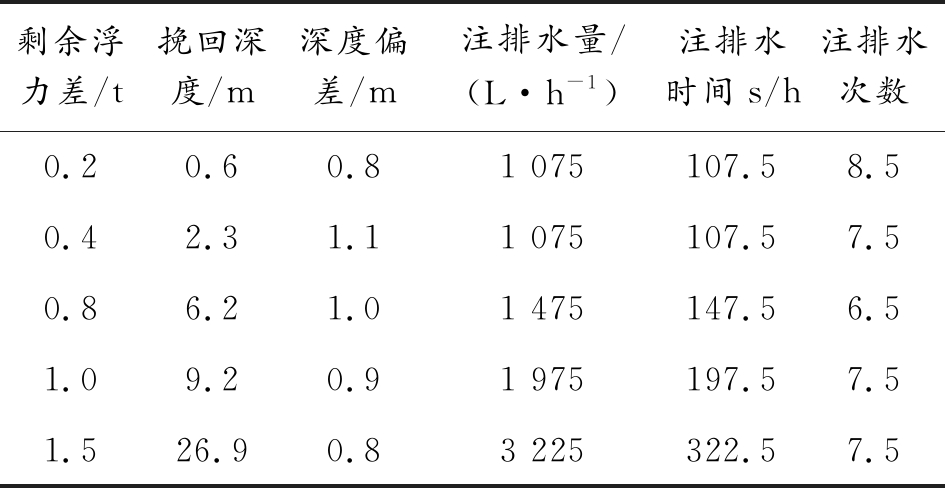
需要特别指出的是，表1及后续表格中的平均注排水量表示单位时间(取1 h)内的平均注排水量，平均注排水时间表示单位时间内的平均注排水时间，平均注排水次数表示单位时间内的平均注排水次数，挽回深度指的是当潜艇存在初始不均衡量时，通过悬停水舱的一次注排水，首次将潜艇深度挽回时潜艇深度与初始时刻时的潜艇深度之间的差值。通过仿真结果可以看出：
1) 剩余浮力差影响最大的是挽回深度、单位时间内平均注排水量和平均注排水时间，剩余浮力差的增加将导致挽回深度、单位时间内平均注排水量和平均注排水时间的迅速增大。剩余浮力差为0.2 t时，挽回深度为0.6 m，单位时间内的平均注排水量和平均注排水时间也分别只有1 075 L和107.5 s；当剩余浮力差为1.5 t时，挽回深度已经增大到26.9 m，单位时间内的平均注排水量和平均注排水时间增大到3 225 L和322.5 s。当剩余浮力差增加到2.0 t时，已经无法控制潜艇深度。
2) 剩余浮力差对悬停深度偏差、最大纵倾角范围和单位时间内平均注排水次数影响不大。随着剩余浮力差的增加，潜艇的悬停深度误差和纵倾角范围能够始终较平稳的保持在±5 m和±1.5°以内，单位时间内平均注排水次数也变化不大，一直保持在7.5次左右。
4.2 剩余力矩差对悬停的影响
当潜艇存在较大的剩余力矩差时，需要通过纵倾平衡系统的纵倾平衡水舱进行调水对潜艇纵倾实施控制，使潜艇纵倾角限制在安全范围以内。图5～图6为初始不均衡力矩分别为-12 t·m、-16 t·m时的悬停仿真曲线。仿真条件设置：海水密度梯度值-0.000 01，目标悬停深度100 m，悬停水舱注排水速率10 L/s，悬停水舱阀门延迟时间6 s，初始不均衡量0.5 t。
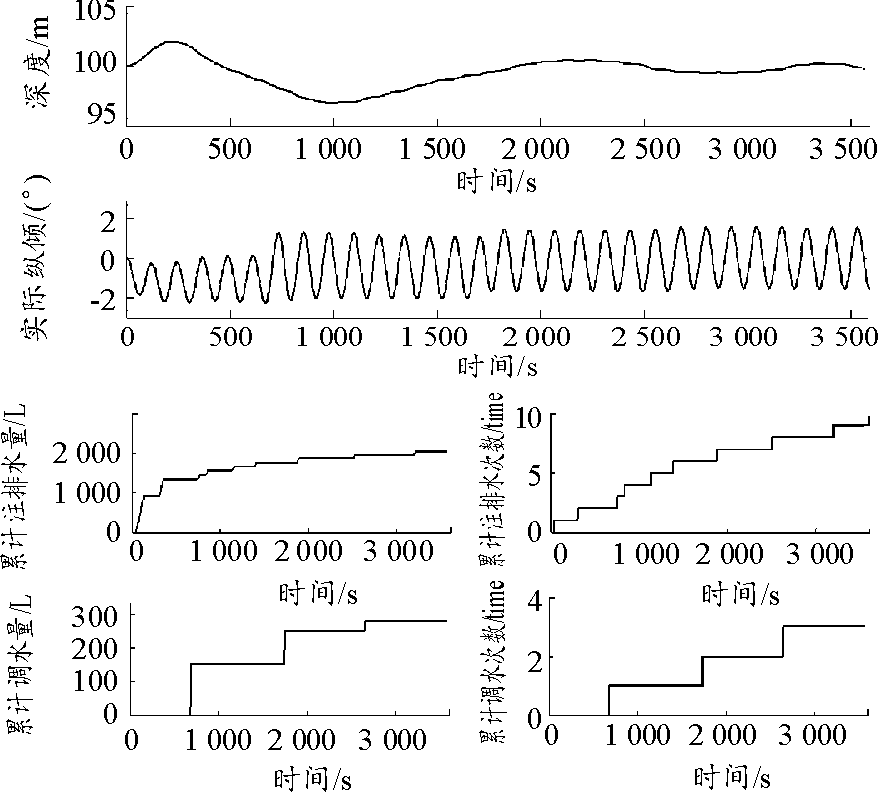
图5 剩余力矩差为-12 t·m时的悬停仿真曲线
Fig.5 Residual torque difference is -12 t·m
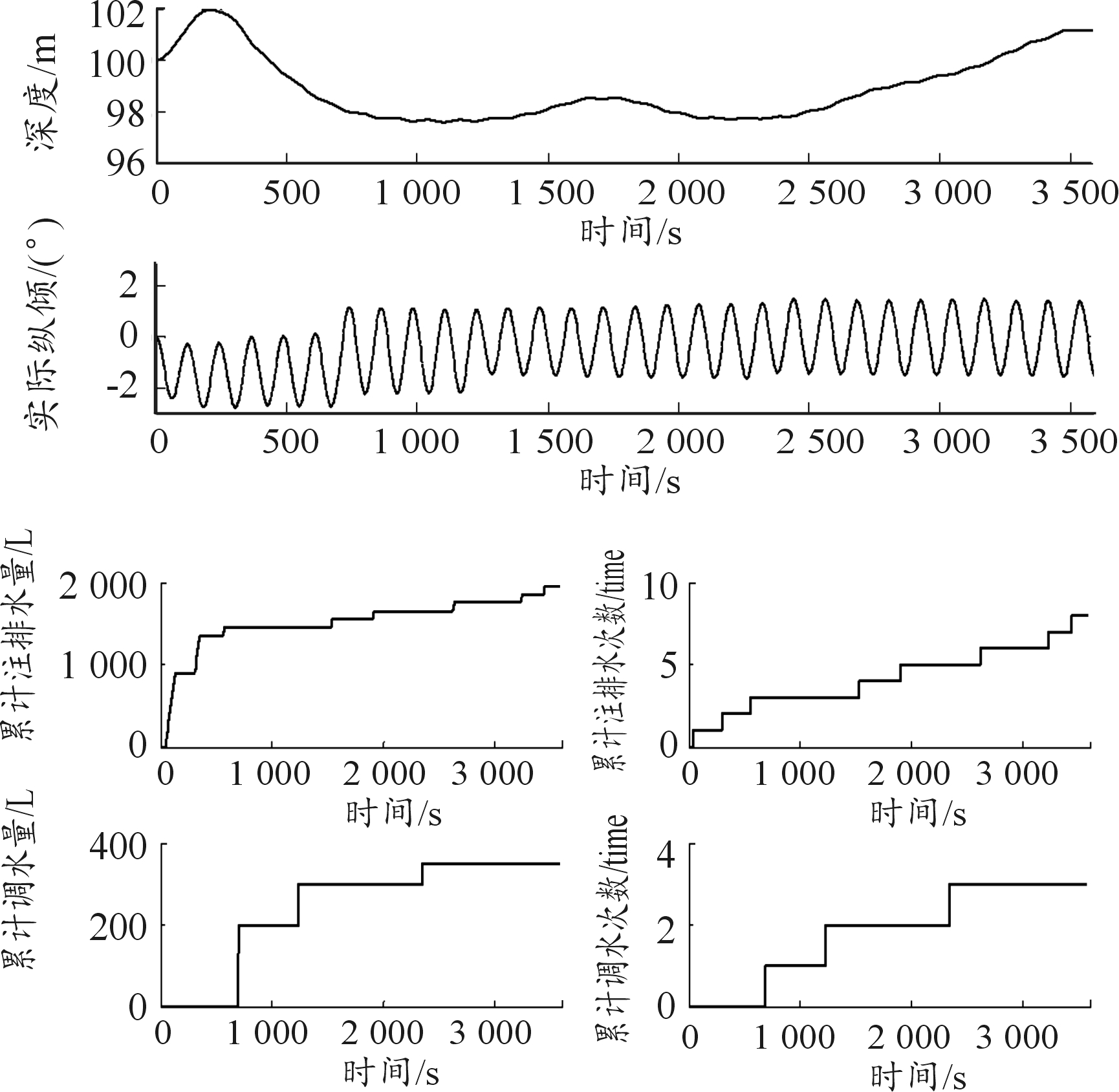
图6 剩余力矩差为-16 t·m时的悬停仿真曲线
Fig.6 Residual torque difference is -16 t·m
表3为剩余力矩差对潜艇悬停影响的仿真结果。
表3 剩余力矩差对潜艇悬停参数的影响数据
Table 3 Influence of residual torque difference on submarine hovering
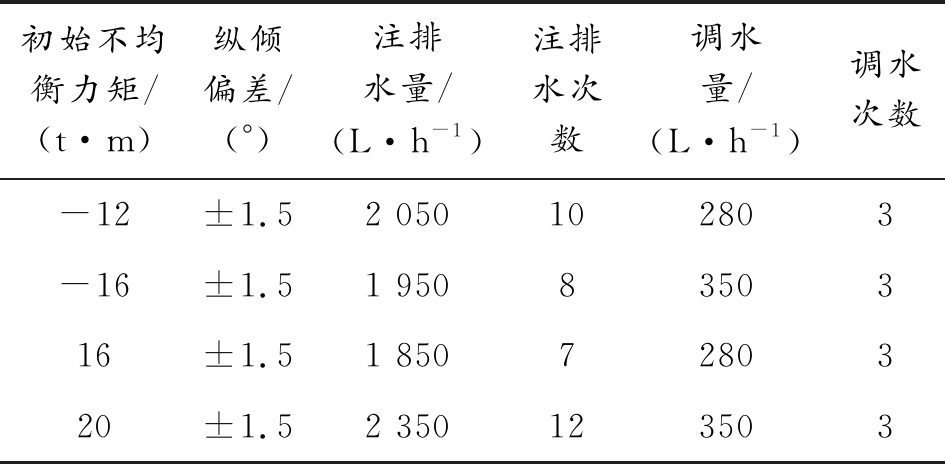
从仿真数据可以看出：
1) 当存在较大的剩余力矩差，潜艇在进行悬停时可引起较大的纵倾角，这时必须使用纵倾平衡水舱通过向首(尾)调水将潜艇纵倾控制在安全范围以内。
2) 当潜艇存在剩余力矩差时，使用纵倾平衡水舱的调水次数一般很少，调水次数基本在5次以内便可将潜艇纵倾控制在±1.5°以内。潜艇悬停时的纵倾是一个周期性的振荡曲线，其振荡周期约为两分钟左右，当通过纵倾平衡水舱的调水平衡掉初始不均衡力矩以后，仅仅依靠潜艇的扶正力矩就能够控制纵倾角保持在要求的范围(±1.5°)以内。
4.3 初始垂速对悬停的影响
所谓初始垂速，是指在即将进入悬停阶段时潜艇的垂速值。有些情况下，剩余浮力差和剩余力矩差为零，由于前潜艇惯性的影响仍然可能存在初始垂速。
图7～9分别为潜艇初始垂速为0.01 m/s、0.04 m/s、0.08 m/s时的悬停仿真图。仿真条件设置：海水密度梯度值-0.000 01，悬停水舱注排水速率10 L/s，目标悬停深度100 m，悬停水舱阀门延迟时间6 s，剩余浮力差和剩余力矩差均为零。
表4为海水密度梯度类型为负梯度条件下(梯度值-0.000 01)初始垂速对潜艇悬停影响的仿真结果。
图7 初始垂速为0.01 m/s时的悬停仿真曲线
Fig.7 Initial vertical speed is 0.01 m/s
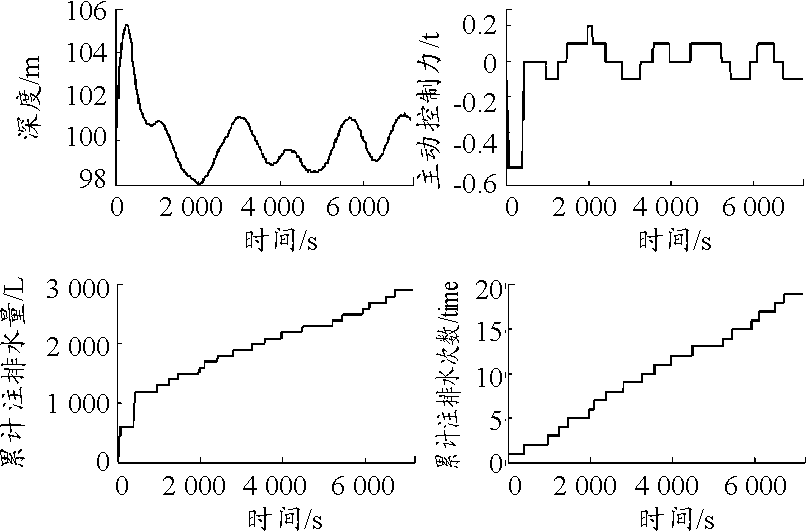
图8 初始垂速为0.04 m/s时的悬停仿真曲线
Fig.8 Initial vertical speed is 0.04 m/s
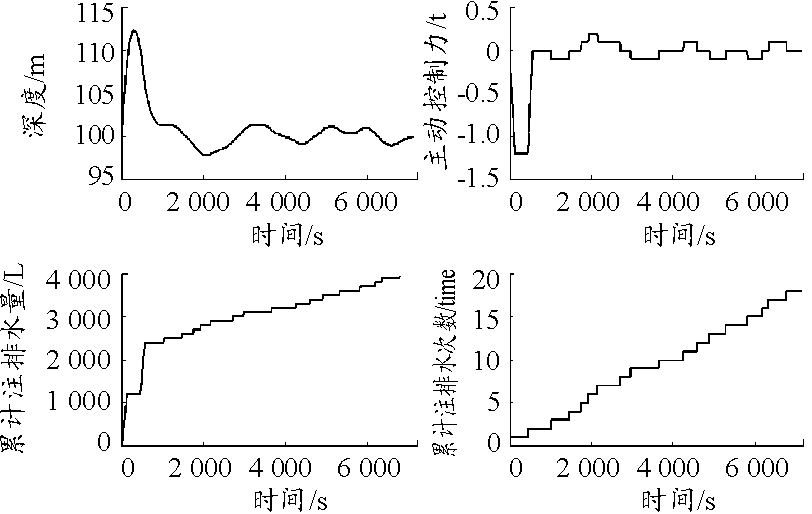
图9 初始垂速为0.08 m/s时的悬停仿真曲线
Fig.9 Initial vertical speed is 0.08 m/s
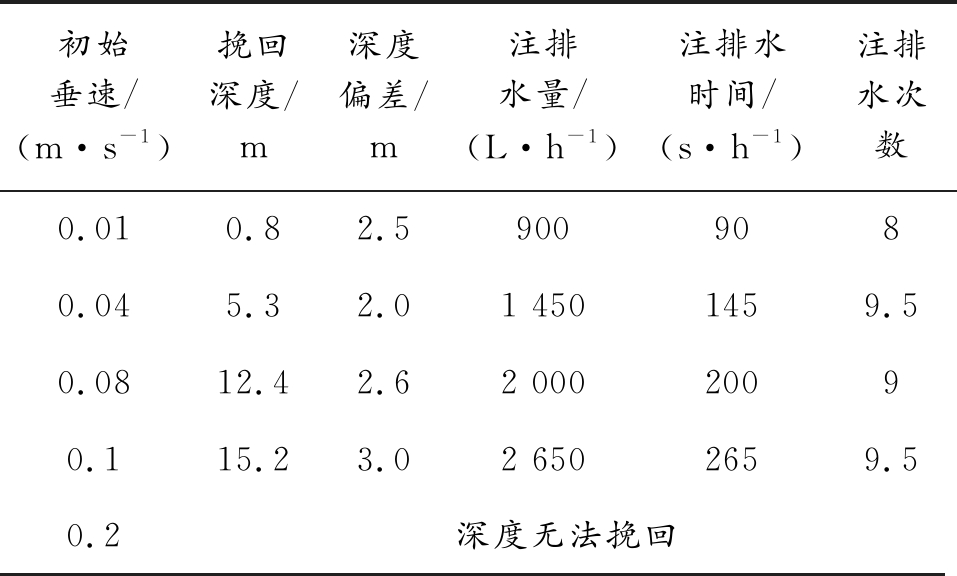
表4 初始垂速对潜艇悬停的影响
Table 4 Influence of initial vertical velocity on submarine hovering
从仿真数据可以看出：
1) 随着初始垂速的增大，挽回深度、单位时间内平均注排水量和平均注排水时间都有明显增大，平均注排水次数也相应有所增加。当初始垂速为0.01 m/s时，挽回深度、累计注排水量、累计注排水时间和累计注排水次数分别为0.8 m、900 L、90 s和8次，当初始垂速增大至0.2 m/s时，深度已经无法挽回(悬停失败)。仿真证明，进入悬停机动前的垂向速度应尽可能控制在0.005 m/s以内。
2) 以最小控制水量100 L为稳定时的潜艇悬停控制量，保证潜艇的垂向运动速度的绝对值不要过大，也就是在潜艇稳定上升过程中需要用2次控制，一次是控制垂速不要过大，一次是使潜艇下潜。
5 结论
1) 为了成功进行悬停机动，初始不均衡量必须保持在一个较小范围内，过大的剩余浮力差和剩余力矩差将会导致挽回深度过大并产生较大纵倾。
2) 垂向速度也是影响潜艇悬停的一个重要因素，过高的垂向速度将会导致大的惯性，增大挽回深度，这对潜艇的悬停是非常不利的。
3) 为了顺利的完成水下悬停机动，在进入悬停机动之前，要求潜艇要准确均衡，尽量保证潜艇的浮力差、力矩差和初始垂速能控制在一个可以接受的范围之内。
[1] 徐亦凡.潜艇操纵原理与方法[M].北京:兵器工业出版社，2002.
Xu Y F.Principle and method of submarine operation[M].Beijing:The Publishing House of Ordnance Industry，2002.
[2] 应东.潜艇水下悬停运动建模与操纵方法研究[J].科学技术创新，2018，34：47-48.
Ying D.Research on modeling and maneuvering method of underwater hovering motion of submarine[J].Scientific and Technological Innovation，2018，34：47-48.
[3] 俞科云，戴余良，施生达.潜艇水下悬停运动控制仿真研究[J].中国舰船研究，2010，5(02):47-48.
Yu K Y，Dai Y L，Shi S D.Simulation research on the motion control of underwater hovering submarine[J].Chinese Journal of Ship Research，2010，5(02):47-48.
[4] 郝英泽，何斌.海水密度变化对潜艇悬停垂向运动的影响仿真研究[J].船海工程，2008，4(02)：117-119.
Hao Y Z，He B.The influence simulation study of the sea density variation upon submarine hovering on the vertical plant[J].Ship & Ocean Engineering，2008，4(02):117-119.
[5] 熊瑛，颜俐，许建.潜艇悬停运动模糊控制[J].舰船科学技术，2013，35(07)：42-50.
Xiong Y，Yan L，Xu J.Research on submarine hovering based on fuzzy control[J].Ship Science and Technology，2013，35(07):42-50.
[6] 施生达.潜艇操纵性[M].北京:国防工业出版社，1995.
Shi S D.Maneuver Ability of Submarine[M].Beijing:National Defense Industry Press，1995.
[7] MUSKER A J，LOADER P R，et al.Simulation of a submarine under waves[J].ISP，1998，35(404)：389-410.
[8] 吴秀恒，刘祖源，施生达，等.船舶操纵性[M].北京：国防工业出版社，2005.
Wu X H，Liu Z Y，Shi S D，et al.Maneuver ability of ship[M].Beijing:National Defense Industry Press，2005.
[9] 张庆国,黄其培,李兴武,等.宽带组合式水声换能器设计研制及应用[J].压电与声光,2020,42(02):223-229.
Zhang Q G.Huang Q P.Li X W.et al.Development and applications of wideband underwater acoustic transducer with combination mode[J].Piezoelectrics & Acoustooptics,2020,42(02):223-229.
[10]孟路，仲晨华.潜艇悬停水舱注排水控制方式比较[J].船海工程，2014，43(04)：160-162.
Meng L，Zhong C H.Comparison of the control mode of water injection and drainage for the submarine hovering water tank[J].Ship&Ocean Engineering，2014，43(04):160-162.
[11]潘国良.潜艇水下悬停运动的操纵控制研究[D].南京：东南大学，2005.
Pan G L.Research on maneuvering control of underwater hovering motion of submarine[D].Nanjing:Southeast University，2005.
[12]赵秀娟.潜艇悬停控制试验系统研究[D].武汉：华中科技大学，2009.
Zhao J J.Research on hovering control test system of submarine[D].Wuhan:Huazhong University of Science and Technology，2009.
[13]张渊博，彭汉国，李春军，等.潜艇悬停注排水估算方程理论推导[J].科技创新导报，2014(09):209-211.
Zhang Y B，Peng H G，Li C J，et al.Derivation of water injection or drainage volume estimating equation during submarine hovering[J].Science and Technology Innovation Herald，2014(09):209-211.
[14]何成，郝英泽，李文龙，等.潜艇悬停数学模型的理论探索[J].四川兵工学报，2009，30(02)：64-66.
He C，Hao Y Z，Li W L，et al.Theoretical exploration of mathematical model of submarine hovering[J].Sichuan Ordnance Journal，2009，30(02):64-66.
[15]朱世开，李明，林莉.基于RBF径向基网络的潜艇水下悬停控制[J].中国水运，2007，1(07)：49-50.
Zhu S K，Li M，Lin L.Submarine hovering system based on RBFNN control[J].China Water Transport，2007，1(07)：49-50.