____________________________________________________________________________________________________________________________________
引用格式:李连升,梅志武,吕政欣,等.X射线脉冲星导航探测技术发展综述[J].兵器装备工程学报,2017(5):1-9.
Citation:format:LI Lian-sheng,MEI Zhi-wu,LYU Zheng-xin, et al.Overview of the Development of X-Ray Pulsar Navigation Detection Technology[J].Journal of Ordnance Equipment Engineering,2017(5):1-9.
______________________________________________________________________________________________________________________________作者简介:李连升(1981—),男,本刊审稿专家,高级工程师,博士,主要从事脉冲星导航技术、航天器优化设计研究。
____________________________________________________________________________________________________________________________________
固体火箭发动机套管型药柱结构的抗冲击研究
摘要:建立了套管型药柱结构的固体火箭发动机燃烧室有限元分析模型,采用冲击响应谱模拟固体火箭发动机受到的外界冲击载荷,分析了固体火箭发动机在横向冲击载荷作用下其药柱、支撑杆的受力、变形。计算结果表明,对于套管型药柱结构的固体火箭发动机,药柱和支撑杆的中部受力和变形最大;随着冲击响应谱斜率增大,套管型药柱的最大应力值逐渐变小。
关键词:冲击响应谱;有限元模型;受力;变形
中图分类号:V11;V57 文献标识码:A 文章编号:2096-2304(2017)05-0001-09
Research on Shock Resistance of Solid Rocket Motor’sCanular Solid Propellant Grains
Abstract: The finite element model of solid rocket motor’s (SRM) combustion chamber with canular solid propellant grains is constructed. The SRM under shock load is simulated by shock response spectrum. The stress and deformation of solid propellant grains and supporting bar are researched with transverse shock load, and results show that the maximum stress and deformation are in the middle of solid propellant grains and supporting bar for canular solid propellant grains solid rocket motor, and the canular solid propellant grain’s maximum stress decreases with the increase of shock response spectrum’s slope.
Key words: shock response spectrum; finite element model; stress; deformation
固体火箭发动机在储存、工作过程中,经常会受到外界冲击载荷的作用,较大的冲击载荷会对发动机的结构产生有害影响,特别是破坏了发动机药柱结构的完整性[1]。为了检验发动机承受冲击载荷的能力,需制定对应的冲击试验规范[2-3]。对发动机进行冲击载荷试验考核,目前使用的方法有冲击波形法、冲击设备法以及冲击响应谱法[4-7]。使用冲击响应谱分析固体火箭发动机在冲击载荷下的响应,可以大大提高计算效率。
冲击响应谱描述了关于单自由度系统受到一系列冲击载荷作用下其物理量(位移、速度或加速度)的最大响应值与系统固有频率之间的函数关系。冲击响应谱是以系统固有频率为横坐标,以单自由度系统响应峰值为纵坐标的曲线。冲击响应谱是由低频段的斜率Φ1 、拐点处的频率f1和高频段的幅值Φ2三个参数描述的一系列曲线[8-9],图1为冲击响应谱试验规范。使用冲击响应谱分析固体火箭发动机所承受的冲击载荷试验,将固体火箭发动机受到的实际时域冲击载荷转化为关于频域的冲击响应谱,然后将冲击响应谱作用在产品上,以此考核发动机的抗冲击载荷能力[10-11]。使用冲击响应谱法模拟实际的冲击效果,一方面考虑了冲击的作用,另一方面考虑了结构的响应,同时将结构的动力学特性与冲击特性有机结合 [12,13]。冲击响应谱法是一种快捷且经济的求解结构响应的方法,其舍去了求解时域下复杂的动力学方程,通过求解系统模态,将模态叠加,即可得到结构响应的最大值。
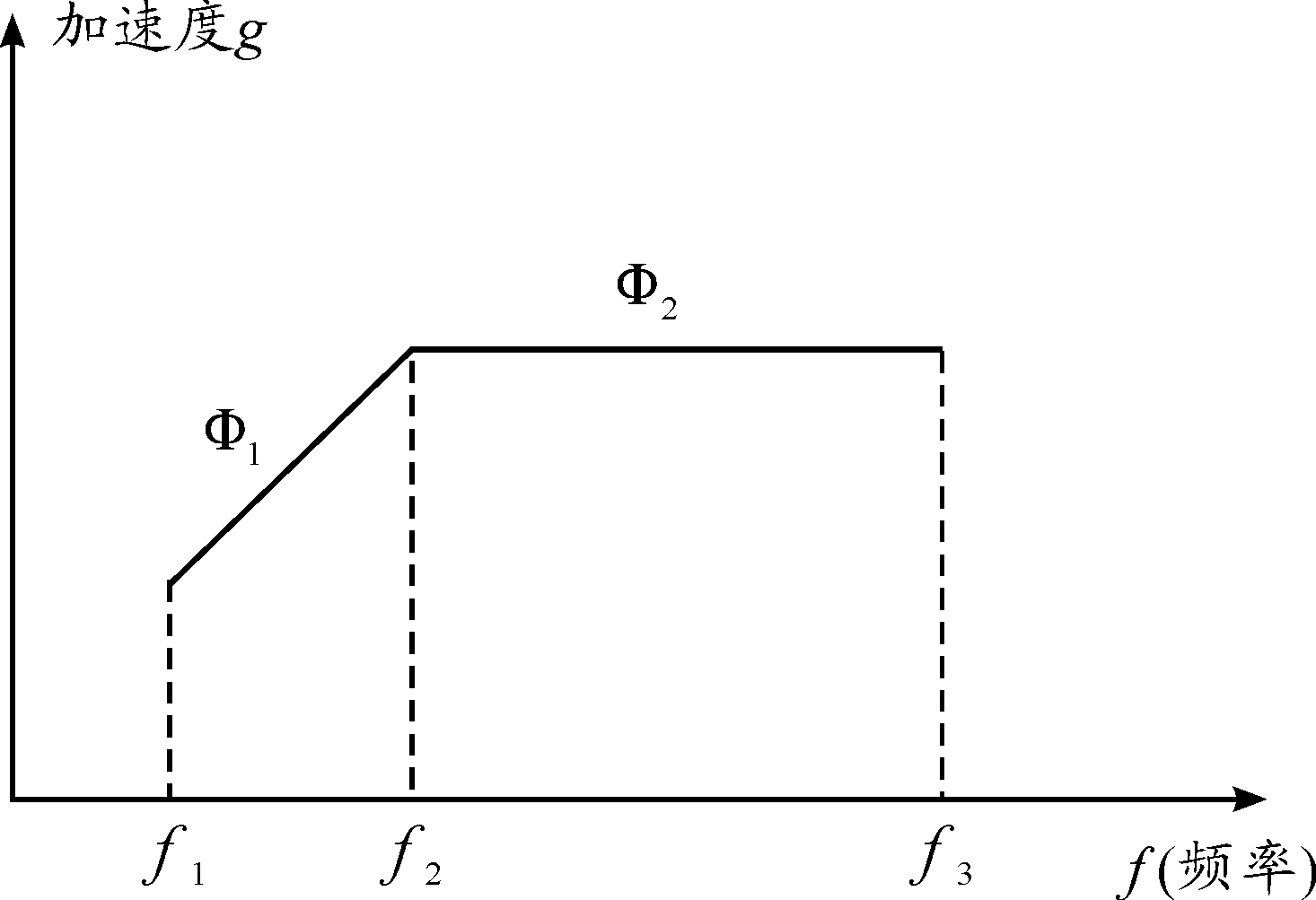
图1 冲击响应谱试验规范
张燕琦[14]使用冲击动力学方法模拟了固体火箭发动机冲击载荷下的响应,由于其求解的是一系列动力学方程,所以计算过程较复杂。李锋等[15]使用冲击响应谱法分析了液体火箭发动机的冲击响应。董龙雷等[16]使用冲击响应谱法分析了高速火箭橇滑轨的冲击响应。对于套管型药柱结构的固体火箭发动机在冲击载荷作用下的响应尚未见到有关文献。套管型药柱结构的固体火箭发动机在冲击载荷作用下药柱的受力、变形比常规药型固体火箭发动机应该更严重。精确计算药柱的冲击响应,可以有效评估药柱的抗冲击性能以及安全裕度。
文中通过建立套管型固体火箭发动机燃烧室的三维有限元分析模型,使用冲击响应谱方法模拟实际冲击环境,计算结构的最大响应值,为套管型固体火箭发动机基于冲击载荷下的结构设计提供理论支持。
1 计算模型
1.1 物理模型
面对称的固体火箭发动机燃烧室如图2所示。燃烧室模型主要由药柱(包扩内药柱和外药柱)、壳体、绝热层、支撑杆以及前堵盖组成。固体火箭发动机通过上支耳和下支耳与飞行器连接在一起工作,飞行器产生的冲击载荷通过支耳传递到固体火箭发动机的燃烧室,燃烧室内部的推进剂由于受到冲击载荷产生应力和变形。
由于冲击载荷的复杂性,对物理模型引入以下简化假设:
1) 由于固体火箭发动机结构和所受载荷面对称,为简化计算量,将模型沿对称面分开,只取实际模型的一半计算。
2) 认为药柱、绝热层、壳体、支撑杆之间的界面在冲击载荷作用下不脱粘。
3) 将两个支耳与飞行器通过螺栓连接简化为支耳中心孔的固支约束条件。
4) 由于冲击载荷作用时间短,将药柱看做线弹性材料。

图2 燃烧室示意图
1.2 冲击响应谱的计算方法
冲击响应谱是指一系列单自由度质量阻尼系统,当其公共基础受到冲击激励时各单自由度系统产生的响应峰值作为单自由度系统固有频率的函数曲线。
对于一个实际的多自由度物理系统,可以将其分解为多个不同的单自由度系统,然后对每个单自由度进行冲击响应分析,得到每个单自由度响应的最大值和与其对应的固有频率,将表示这些值的数据点用光滑曲线连接即可得整个系统在特定冲击激励下的的冲击响应谱。
x(t)将物理系统分解成包含有n个不同固有频率的单自由度系统,而每个子系统都可以简化成质量—弹簧—阻尼模型。单自由度质量—弹簧—阻尼系统受基础激励冲击的物理模型图3所示。计算得到其相应x(t)为:
x(t)=Ae-2ξωntsin(![]() t+α)+Bsin(ωt+φ)
t+α)+Bsin(ωt+φ)
(1)
式中, ωnωn=2πfn,其中ωn为系统的固有圆频率, fn表示系统的固有频率,令 fn= f1,求解式(1)可以得到x1(t),找出其最大值![]() 同理,设 fn=f2,得到
同理,设 fn=f2,得到![]() 直到求出
直到求出![]() 在对数坐标系下做出
在对数坐标系下做出![]() 的曲线,即可得到特定冲击激励载荷下的冲击响应谱曲线(位移响应谱曲线)。对式(1)中的x(t)依次求一阶导数和二阶导数,并按求解位移响应谱曲线的方法,得到速度响应谱曲线和加速度响应谱曲线。图1为加速度响应谱曲线的一般形式,一般低频部分使用斜率Φ1 表示,斜率单位为dB/oct,表示分贝每倍频,其计算方法为Φ1=10×lg(Φ2/Φ3)/log2(f2/f1),其中Φ3 表示频率f1对应的加速度幅值。
的曲线,即可得到特定冲击激励载荷下的冲击响应谱曲线(位移响应谱曲线)。对式(1)中的x(t)依次求一阶导数和二阶导数,并按求解位移响应谱曲线的方法,得到速度响应谱曲线和加速度响应谱曲线。图1为加速度响应谱曲线的一般形式,一般低频部分使用斜率Φ1 表示,斜率单位为dB/oct,表示分贝每倍频,其计算方法为Φ1=10×lg(Φ2/Φ3)/log2(f2/f1),其中Φ3 表示频率f1对应的加速度幅值。
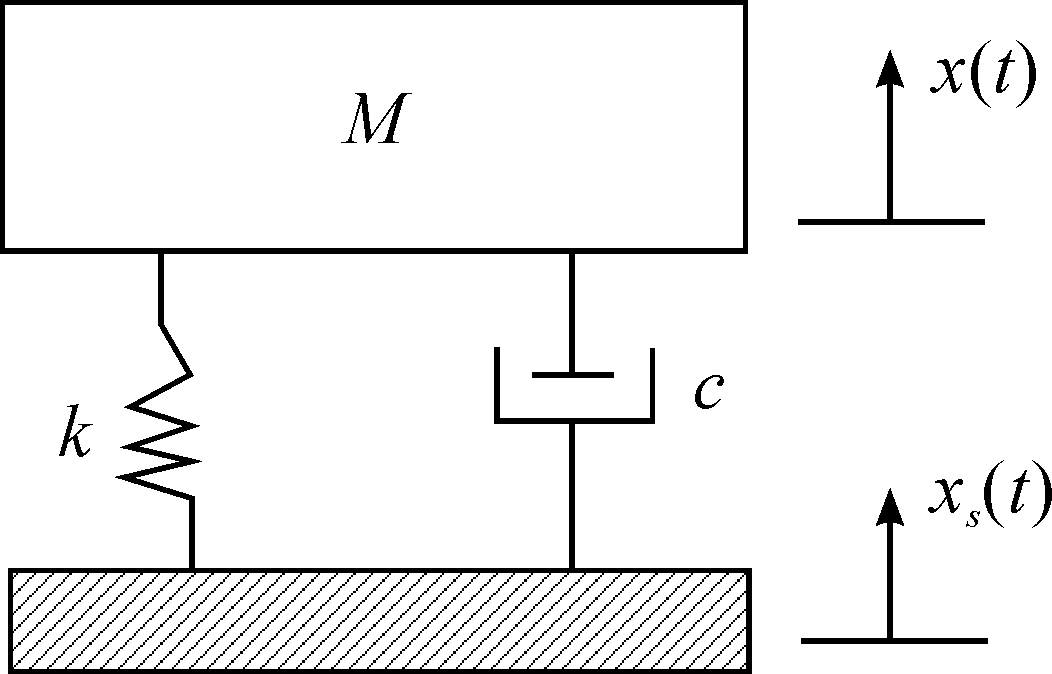
图3 单自由度质量-弹簧-阻尼系统物理模型
1.3 控制方程
三维线弹性动力学的控制方程为:
平衡方程为
σij, j+fi=ρui,tt+μui,t (在V域内)
(2)
几何方程为
εij=![]() (ui, j+uj, i) (在V域内)
(ui, j+uj, i) (在V域内)
(3)
物理方程为
ui,tui,ttσij=Dijklεkl (在V域内)
(4)
式中, ρ是质量密度; μ是阻尼系数; ui,tt和 ui,t分别是ui对t的二阶导数和一阶导数,即分别表示i方向的加速度和速度。
1.4 边界条件和冲击载荷条件
1) 上、下支耳固定条件:上、下支耳平动位移,转动位移均被约束为零;
2) 面对称条件:垂直对称面方向的平动位移为零,对称面内的转动位移为零;
3) 基础运动条件:基础的运动激励通过上、下支耳传递到固体火箭发动机燃烧室,由加速度响应谱给出,品质因数Q=10,见表1所示。
表1 冲击试验条件

2 计算方法
冲击响应谱方法经济方便,可以快捷的求解出结构在外界载荷激励下的峰值响应值,如位移、应力等物理量。首先计算结构系统的各阶模态,然后通过模态振型叠加计算结构在冲击载荷作用下的响应值。
本文使用有限元计算结构响应,对模型离散化后,结构系统的自由振动方程为:
[M]{u″}+[C]{u′}+[K]{u}=0
(5)
求解上式可以得到第任意α阶模态以及此阶模态下的系统固有频率wα。
在相应谱分析中,首先计算在某一方向(设为k方向)的冲击响应谱作用下,第α阶模态产生的响应峰值:
(6)
其中![]() 为在α阶模态下,固有频率为wα,阻尼为ξα时响应谱的值,ck为缩放比例系数
为在α阶模态下,固有频率为wα,阻尼为ξα时响应谱的值,ck为缩放比例系数![]() 为k方向与j(j=x,y,z)方向的方向余弦, Γαj为α阶模态在j(j= x,y,z)方向上的分配系数。
为k方向与j(j=x,y,z)方向的方向余弦, Γαj为α阶模态在j(j= x,y,z)方向上的分配系数。
本文的计算中,k方向为坐标系的y方向,所以式(6)即为:
(7)
第α阶模态下的响应峰值![]() 可以通过将所有方向冲击载荷作用下的响应值叠加:
可以通过将所有方向冲击载荷作用下的响应值叠加:
(8)
对于本文的计算工况而言,因为冲击响应谱只在y方向上作用,所以式(7)即为:
(9)
将各阶模态下的![]() 叠加,可以得到某一物理量R在y方向的响应谱激励下的峰值
叠加,可以得到某一物理量R在y方向的响应谱激励下的峰值![]() 叠加的方式较多,有绝对值相加法、平方根相加法以及完全二次方程合并法等,本文计算采用平方根相加法:
叠加的方式较多,有绝对值相加法、平方根相加法以及完全二次方程合并法等,本文计算采用平方根相加法:
(10)
3 算例验证
根据文献[17]中对简支梁的计算,图4中简支梁的横截面积为355.6 mm×37 mm,梁的材料密度为1.047 3 × 105 kg/m3,梁基础的加速度载荷(图4中 ys)沿垂直方向施加在梁的两个简支点。
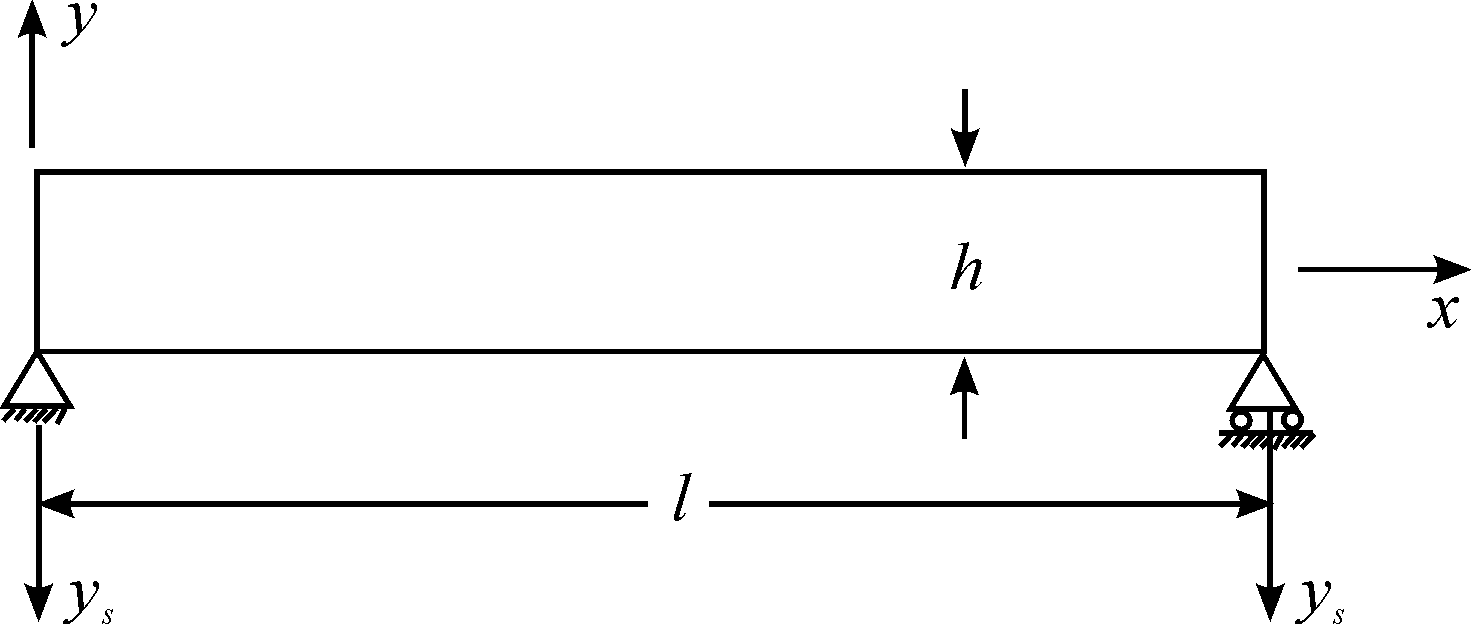
图4 响应谱测试的简支梁
梁所受到的载荷为动载荷,梁基础的加速度载荷曲线如图5。通过上一节求冲击响应谱的计算方法,可以得到其对应的加速度响应谱值,见表2。
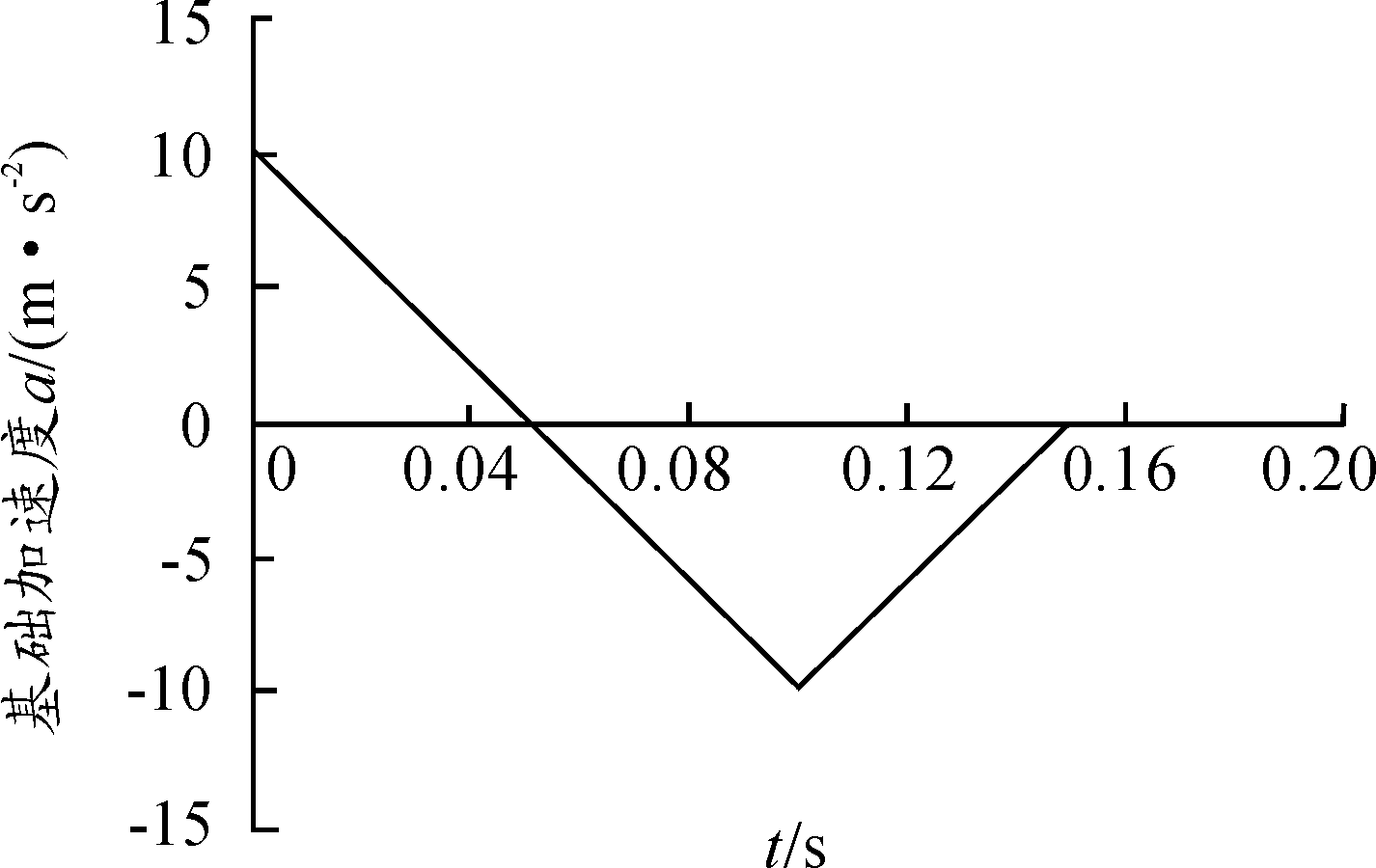
图5 梁基础的加速度载荷曲线
表2 加速度相应谱

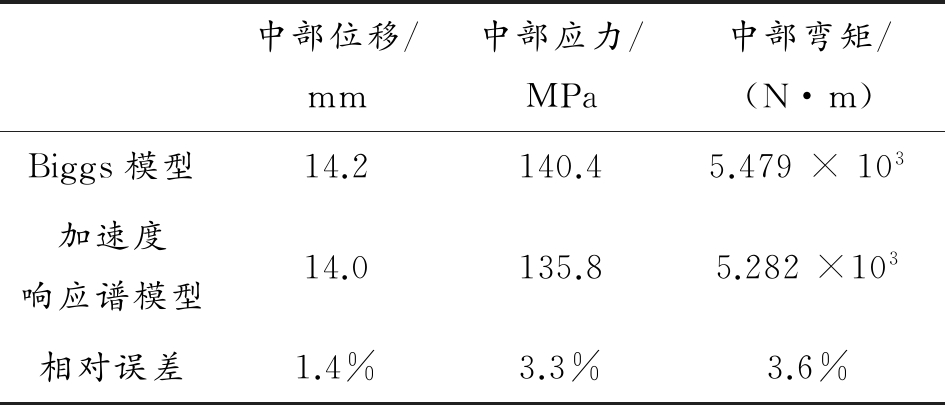
根据文献计算的结果与使用加速度响应谱计算的结果见表3,从表3可以看出使用加速度响应谱计算结果得到的中部位移、中部应力、中部弯矩值均相互接近,误差最大仅为3.6%,本算例验证了使用加速度响应谱模拟计算结构受冲击载荷的有效性。
表3 计算结果对比
4 计算结果及分析
4.1 计算参数选取
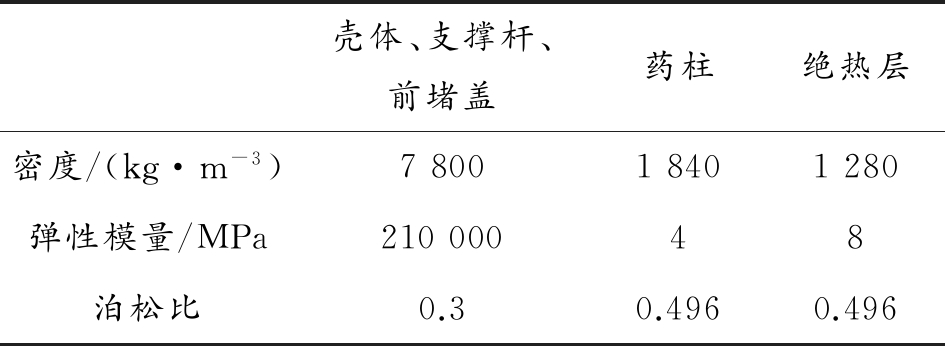
燃烧室的示意图见图2。据此构建有限元分析模型,模型离散为三维实体单元,单元总数大约8万个。本计算模型中,各部件的材料参数值如表4。冲击载荷条件和边界条件见1.4节。计算时,先进行模态分析,计算出系统的前1 000阶模态,特征值的求解使用Lanczos方法。
表4 计算材料参数
4.2 药柱在纵向冲击载荷作用下的计算结果分析
外部环境的冲击载荷通过燃烧室壳体的两个支耳传递至推进剂,推进剂产生应力、变形。本文采用冲击响应谱首先求解燃烧室结构的各阶模态,然后求解各阶模态对结构响应的贡献值,并将各模态叠加起来,从而得到燃烧室结构的响应值。
图6为在纵向冲击载荷作用下,燃烧室内药柱的横向位移分布云纹图。可以看出,在纵向冲击载荷作用下,燃烧室内药柱可以近似看做是两端固定的横梁,在惯性力作用下产生横向弯曲,药柱中部挠度最大,中部纵向最大挠度2.16 mm。由于内药柱中部弯曲程度最大,造成药柱中部Mises应力最大,内药柱Mises应力分布云纹图见图7。由图7可见,药柱中部Mises应力最大值为0.123 MPa,位于药柱中部内孔处。
内药柱Mises应力沿药柱内孔轴向变化曲线见图8,由曲线可见,内药柱Mises应力分布基本上呈左右对称。

图6 内药柱的纵向位移分布云纹图(单位:mm)

图7 内药柱的Mises应力分布云纹图(单位:MPa)
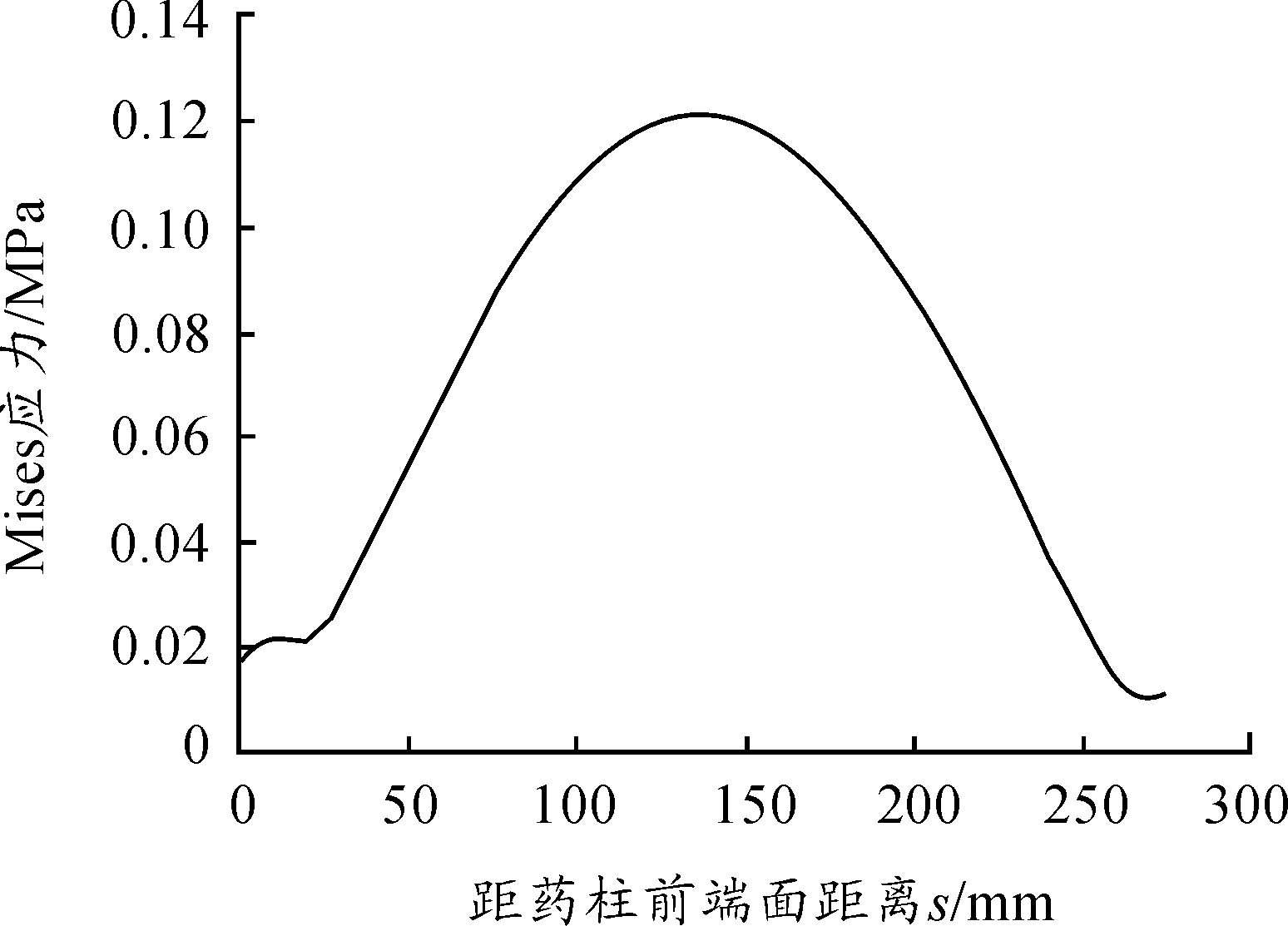
图8 内药柱的Mises应力沿药柱内孔轴向变化曲线
图9为冲击载荷作用下,外药柱Mises应力云纹图。由图9可以发现,外药柱最大应力位于靠近支耳部位,但是外药柱最大应力值较小,仅为0.001 5 MPa,可以认为外界冲击载荷对外药柱的影响较小。由于外药柱与壳体之间存在绝热层,当外载荷通过壳体传递到药柱时,绝热层对药柱有缓冲作用。同时,外药柱在纵向与绝热层粘接,纵向位移受到限制,而内药柱纵向没有约束,所以内药柱纵向刚度比外药柱低。在纵向冲击载荷作用下,内药柱会外药柱变形更大,应力更大。
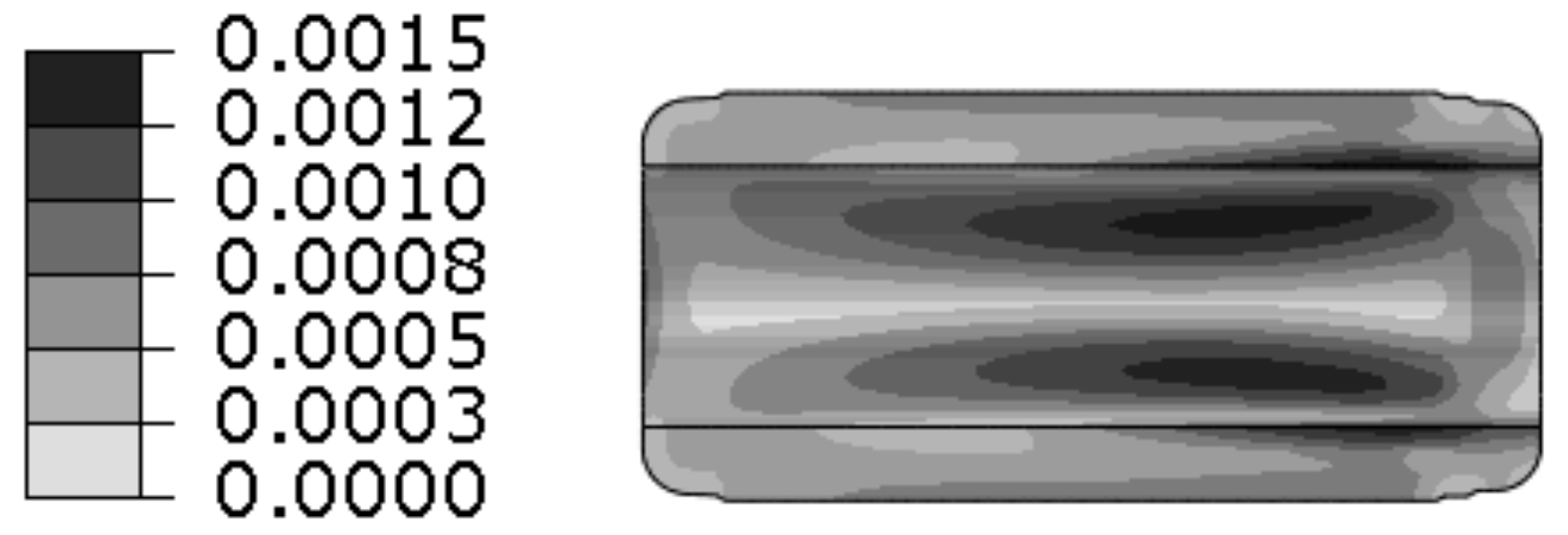
图9 外药柱的Mises应力分布云纹图(单位:MPa)
4.3 支撑杆在纵向冲击载荷作用下的计算结果分析
图10为在纵向冲击载荷作用下,支撑杆沿Y方向的位移分布云纹图。可以看出,支撑杆在Y方向上的变形规律与内药柱变形规律相似,都是中部沿Y方向产生弯曲变形,支撑杆中部位移最大,为1.08 mm。
图11为支撑杆Mises应力分布云纹图。可以看出,在Y向冲击载荷作用下,支撑杆应力最大值的位置在图中A处,Mises应力值为240 MPa。支撑杆中部应力值也较大,为178 MPa。所以在支撑杆结构设计中,需要考虑增加A处的结构强度,适当降低应力值,防止在冲击过程中发生断裂,造成药柱失稳,影响发动机正常工作。
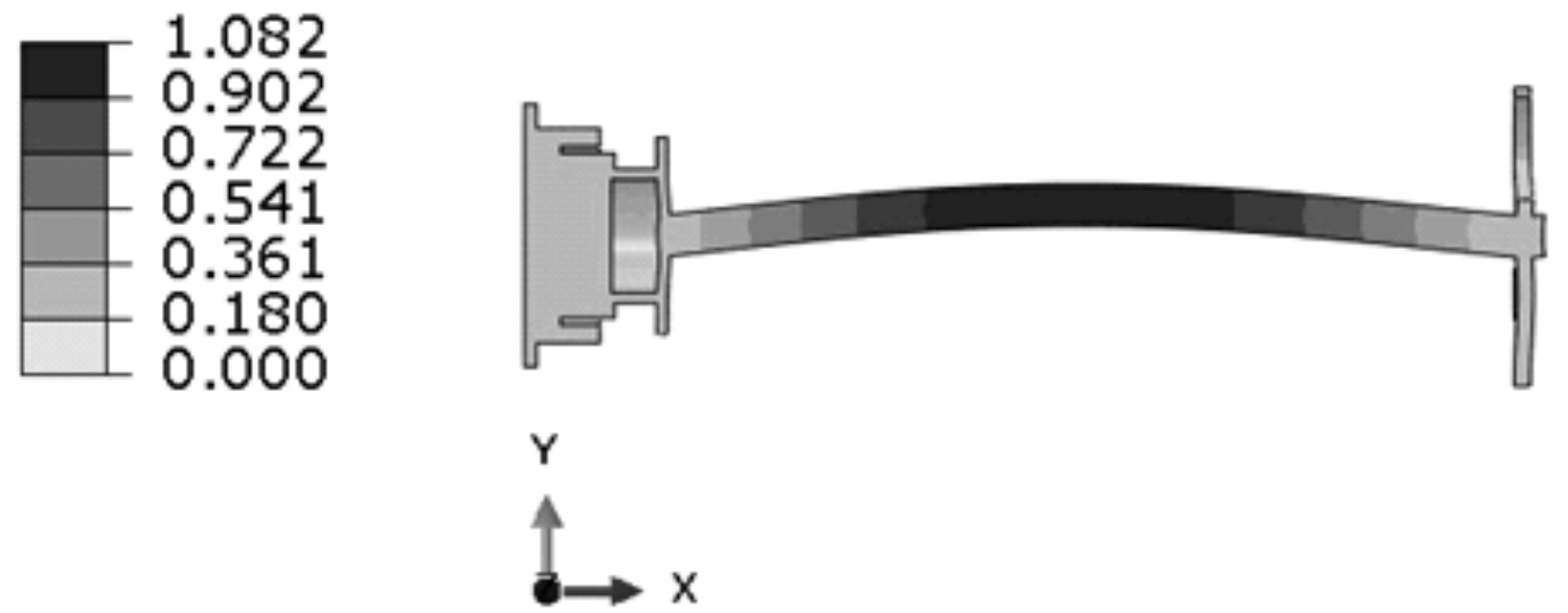
图10 支撑杆沿Y方向的的位移分布云纹图(单位:mm)
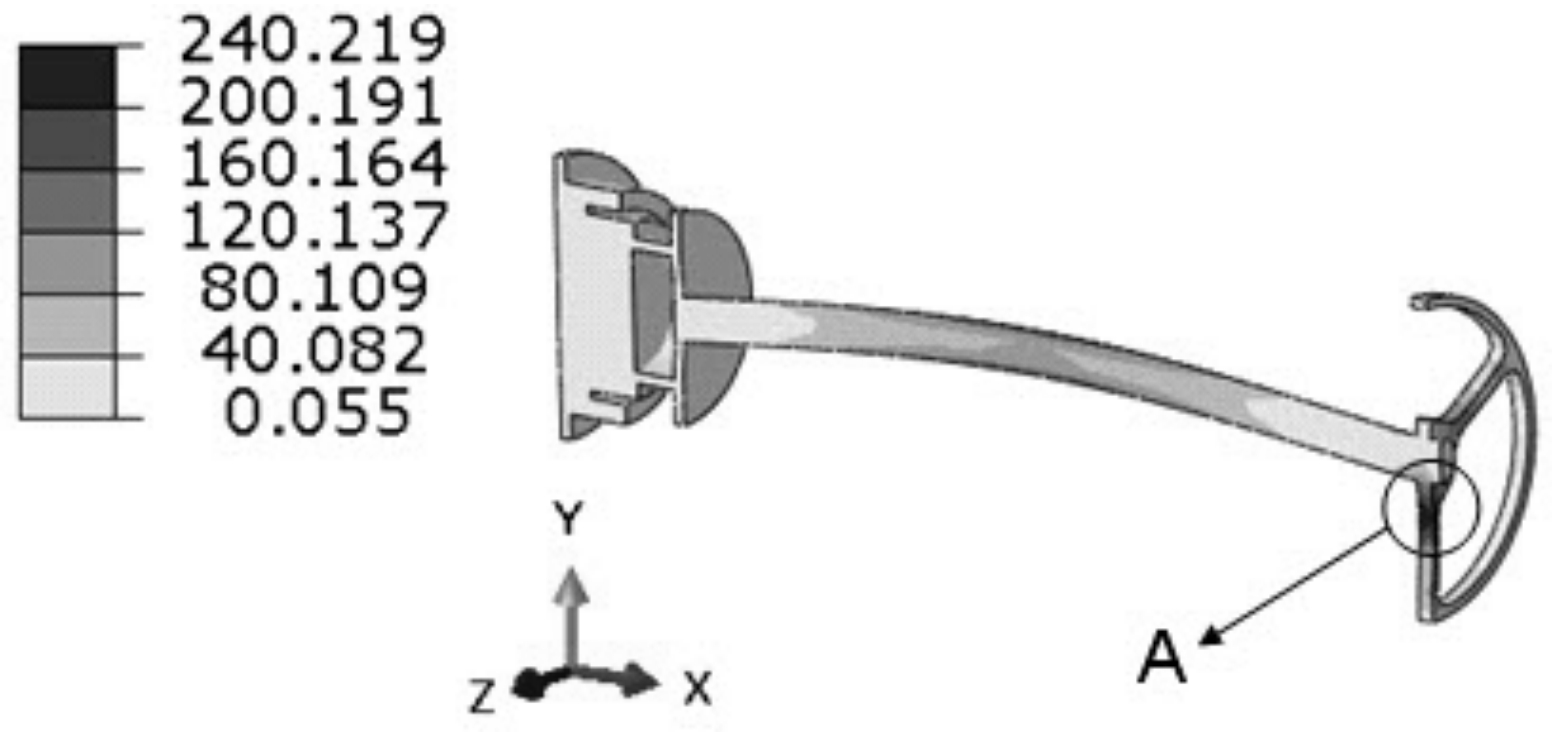
图11 支撑杆的Mises应力分布云纹图(单位:MPa)
4.4 冲击响应谱斜率大小对结构响应的影响
图12是斜率为9 dB/oct下内药柱Mises应力分布云纹图。可以看出,改变冲击响应谱的斜率,其药柱的应力分布规律基本一致,但是应力的大小值发生变化。这说明冲击响应谱的斜率只是反映了冲击载荷传递到发动机后的强度大小,冲击模式没有发生变化。

图12 斜率为9 dB/oct下内药柱的Mises应力 分布云纹图(单位:MPa)
图13为不同斜率的冲击响应谱下的药柱最大Mises应力曲线。可以看出,随着冲击响应谱斜率增大,药柱的最大Mises应力值逐渐变小。一般与固体火箭发动机连接的飞行器的阻尼直接影响冲击响应谱的上升斜率,阻尼越大,上升斜率越大,对应的结构响应值变小。所以,在结构设计过程中,适当增大结构阻尼值,可以降低冲击载荷对固体火箭发动机药柱的影响。
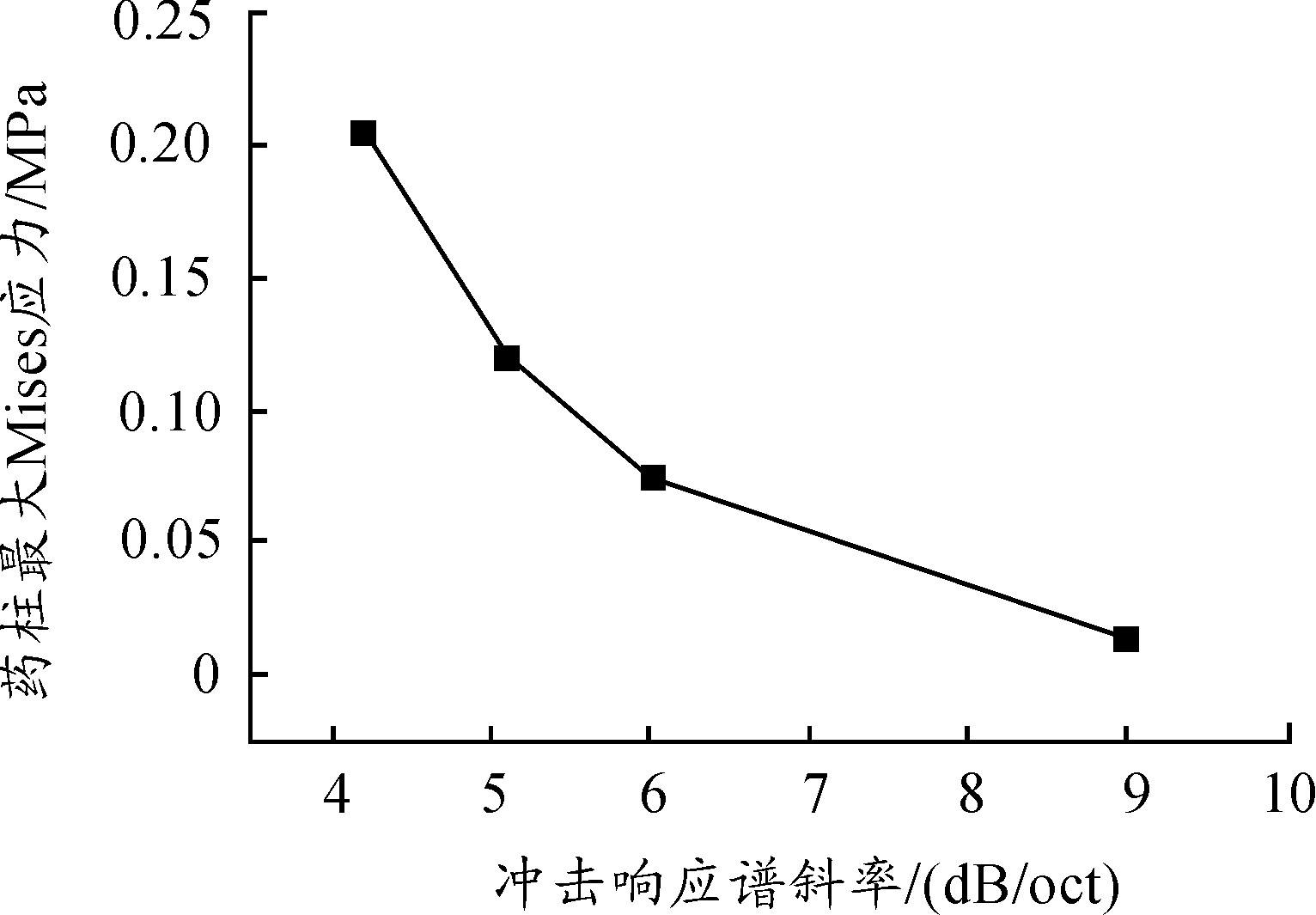
图13 药柱最大Mises应力-冲击响应谱斜率曲线
5 结论
通过建立套管型药柱结构的固体火箭发动机承受冲击载荷的有限元模型,采用冲击响应谱分析了发动机的力学性能,得到如下结论:
1) 建立基于冲击响应谱下的固体火箭发动机药柱结构完整性的有限元模型,有限元计算结果和计算结果对比显示两者误差较小,验证了有限元计算模型的可行性。
2) 套管型药柱结构的固体火箭发动机在纵向冲击载荷作用下,内药柱产生的应力、位移均比外药柱大,外药柱产生的应力、位移非常小。
3) 套管型药柱结构的固体火箭发动机在纵向冲击载荷作用下,应力集中在支撑杆靠近车轮处的A处,在支撑杆设计过程中需重点考虑增加此处的强度。
4) 随着冲击响应谱斜率增大,药柱Mises应力值逐渐变小,结构设计中适当增加结构阻尼,可以减少套管型药柱结构的固体火箭发动机对冲击响应值的大小。
参考文献:
[1] 张建华.航天产品的爆炸冲击环境技术综述[J].导弹与航天运载技术,2005(3):30-36.
[2] 卢来洁,马爱军.冲击响应谱试验规范述评[J].振动与冲击,2002,21(1):18-31.
[3] 朱子宏.大型航天产品冲击响应谱试验方法探讨[J].航天器环境工程,2001,68(3):49-54.
[4] 任昌,潘宏侠.基于冲击信号的冲击响应谱研究[J].火炮发射与控制学报,2010,21(3):21-24.
[5] 王翠荣,施广富,郭军.固体火箭发动机冲击信号响应谱分析[J].固体火箭技术,2003,26(2):57-60.
[6] 穆瑞忠,张建华,皮本楼.航天器的冲击谱模拟试验方法[J].强度与环境,2008,35(5):32-37.
[7] 都军民,戴宗妙.冲击响应谱在冲击试验中的应用研究 [J].舰船科学技术,2007,29(1):19-21.
[8] 华师韩,田恒春.冲击响应谱计算相关参数选择的研究[J].遥测遥控,2005,26(6):52-57.
[9] 刘继承,黄光萍.冲击响应谱试验参数的设置[J].现代雷达,2010,32(2):91-94.
[10] 郭勤涛,张令弥.以冲击响应谱为响应特征的有限元模型确认[J].振动与冲击,2005,24(6):32-36.
[11] 王冰,田振强,张巧寿.摆锤式冲击响应谱试验台的仿真研究[J].强度与环境,2012,39(3):26-31.
[12] YANG Zhengwen.Finite element simulation of response of buried shelters to blas loadings[J].Finite Elements in Analysis and Design,1997(24):113-132.
[13] LIANG Chochung,YANG Minfang.Prediction of shock response for a quadrupod-mast using response spectrum analysis method[J].Ocean Engineering,2002,29:87-914.
[14] 张燕琦,徐秉恒.固体火箭发动机轴向冲击响应有限元分析[J].固体火箭技术,2006,29(6):400-403.
[15] 李锋,邓长华,鲍福廷.液体火箭发动机冲击响应谱分析计算方法[J].西安工业大学学报,2009,29(1):28-31.
[16] 董龙雷,张静静,赵建平.基于冲击响应谱的高速火箭橇滑轨路谱分析[J].西南交通大学学报,2015,50(6):1170-1174.
[17] BIGGS J M.Introduction to Structural Dynamics[M].McGraw-Hill,1964:256-263.
