____________________________________________________________________________________________________________________________________
引用格式:张浩,闻泉,王雨时,等.炮射子母弹定时开舱高度散布仿真[J].兵器装备工程学报,2017(10):46-49.
Citation formatZHANG Hao,WEN Quan,WANG Yushi, et al.Simulation Research on Dispersion of Opening Height of Gun Launched Submunition Carrier Projectile with Time Fuze[J].Journal of Ordnance Equipment Engineering,2017(10):46-49.
______________________________________________________________________________________________________________________________作者简介:张浩(1992—),男,硕士研究生,主要从事引信、弹药技术研究。
____________________________________________________________________________________________________________________________________
炮射子母弹定时开舱高度散布仿真
摘要:基于6自由度弹道方程,采用符合误差因素分布特征的随机数,运用蒙特卡罗方法建立炮射子母弹定时开舱高度散布仿真预测模型。以某155 mm口径火炮为例,分别得到了最大射程、最大射程2/3处、最大射程1/2处和最大射程1/3处定时开舱高度散布的仿真数值。结果表明:以最大射程、最大射程2/3的射程射击时,开舱高度散布受纵风影响较大,而最大射程1/2、1/3处,装定时间散布是影响开舱高度散布的主要因素;配定时开舱引信的炮射子母弹不适合以最大射程攻击目标。
关键词:子母弹;开舱高度;6自由度弹道模型;蒙特卡罗方法;仿真
中图分类号:TJ013.2 文献标识码:A 文章编号:2096-2304(2017)10-0046-04
Simulation Research on Dispersion of Opening Height ofGun Launched Submunition Carrier Projectile with Time Fuze
Abstract: The 6-DOF trajectory equation were applied, and the simulation predicition model for dispersion of opening height of gun launched submunition carrier projectile was established by using Monte-Carlo method and applying random number series according to the feature of error factor. The corresponding dispersion simulation values under one-third firing-range, a half firing-range, two-thirds firing-range and maximum firing-range were obtained taking a 155 mm caliber gun for a numerical example. The result shows that the maximum firing-range and two-thirds firing-range vertical dispersion of opening height is influenced greatly by longitudinal wind. And the spread in timer time has a great impact on the vertical dispersion under one-third firing-range and a half firing-range. The gun launched submunition carrier projectile is unfit to attack target with the maximum firing-range.
Key words: submunition carrier projectile; opening height; 6-DOF trajectory model; Monte-Carlo method; simulation
按照子母弹飞行过程,子母弹弹道主要由一条母弹弹道和由母弹抛出许多子弹形成的集束弹道所组成[1]。使用子母弹射击时,在一定的初速、射角下子母弹从炮口飞出,在时间引信的作用下,子母弹在目标区域的预计高度上开舱抛出子弹[2]。但由于该预计高度是由时间引信定时实现的,所以在实际射击过程中,会因各种散布因素的影响,使子母弹并不能严格地在预定高度开舱,而是存在开舱高度高低散布的现象。在子母弹靶场试验中,现场测量出子母弹开舱高度高低不一,有些弹甚至落地还没有开舱[3-4]。文献[3-4]以某型火炮为例,综合分析影响子母弹开舱高度各种因素的概率误差和敏感因子,运用误差合成的方法计算并分析了某火炮子母弹开舱高度的高低散布随高度、初速和射角的变化及各因素所占的比重,提出了子母弹最低开舱高度的确定方法,但未考虑纵风对开舱高度高低散布的影响。本文以某155 mm口径火炮为研究对象,利用Matlab软件建立外弹道弹丸6自由度刚体运动方程,综合考虑影响子母弹开舱高度的各种因素,运用蒙特卡洛方法,对一定条件下子母弹开舱高度进行仿真,分析子母弹开舱高度的高低散布。
1 理论分析
1.1 6自由度弹道方程[5]
6自由度弹道方程具有较高的精度,可用于射表编制,能够完整描述弹丸在空中的各种动态过程。本文对弹丸及飞行条件作如下假设:
1) 气象条件是标准的,且风速恒定;
2) 弹丸质量分布均匀且轴对称,刚体;
3) 地表为平面,重力加速度为常数,方向铅直向下;
4) 忽略科式惯性力的影响。
1.2 开舱高度影响因素分析
1.2.1 弹道散布引起的开舱高度高低散布
弹道散布是发射过程中初速、射角、弹道系数和风等因素引起的。在弹道学和射击学中,落点的散布通常用中间误差E表示,对于子母弹,其开舱高度散布仍用中间误差E表示。子母弹飞行过程中,在时间引信的作用下,母弹在空中开舱抛出子弹,弹道散布会引起子母弹开舱点高度的高低散布。影响子母弹开舱高度弹道散布的因素主要有[6-11]:
1) 初速散布Ev0。初速散布是由火药性质、装药结构、点火传火、弹炮相互作用、膛压特性、后效期以及起始段章动特性等散布因素综合作用的结果;
2) 射角散布Eθ0。射击时炮身的随机弯曲、炮身振动、火炮后坐、高低机和方向机空回、火炮放列的倾斜度、弯曲等因素共同作用形成射角散布;
3) 弹道系数散布Ec。弹道系数(c=id2×103/m, i=cx0(1+kδ2)/cx0n)的随机变化是由弹丸直径d、弹丸质量m和阻力系数cx0(1+kδ2)引起的,后者又与弹丸结构参数和攻角的大小有关。弹丸结构参数带来的随机误差主要影响弹丸飞行稳定性,引起阻力等气动力的变化,造成弹道散布。弹丸直径、质心位置、质量偏心、动不平衡角、赤道转动惯量和极转动惯量等在工程实践中随机变化范围小,对弹道散布影响很小,可以忽略,而弹丸质量的随机变化对弹道散布影响较大。文献[9]和文献[11]中在建立地面密集度预测模型时均将弹道系数散布Ec用弹丸质量散布Em近似代替,本文也借鉴这一做法,用弹丸质量散布Em近似代替弹道系数Ec对弹道散布的影响;
4) 纵风散布EWx。
1.2.2 引信装定时间散布引起的开舱高度高低散布
无论是机械时间引信还是电子时间引信,都存在引信计时散布。机械时间引信的定时散布较大,电子时间引信的定时散布较小,引信装定时间散布将引起子母弹开舱点高度的高低散布[4]。
1.2.3 开舱高度的综合高低散布
由于弹道散布的误差源与引信装定时间散布的误差源不相关,所以根据误差合成方法,可用几个综合参数的微小变化(如初速、射角、弹质量等散布)分析和计算开舱高度散布。子母弹开舱点高度的综合高低散布概率误差可写为[4]
Ey=![]() =
=![]()
式中:αi代表各误差源; Eyαi为各误差源引起的开舱高度散布。
2 仿真模型与方法
本文运用蒙特卡罗方法计算子母弹开舱高度散布的思路如下[11-14]:
1) 基于文献[5]中的6自由度弹道模型,建立弹丸6自由度外弹道方程;
2) 根据弹道散布各误差影响因素的分布规律,结合蒙特卡洛方法,生成符合各误差因素分布类型及统计特性的随机数序列来描述各误差因素的分布;
3) 设预计开舱高度为H,取标准弹道的弹道高H处的时间为定时时间t,将各伪随机数序列分别代入外弹道方程,取时间t处的高度为子母弹的开舱高度;
4) 根据由3)得到的一系列数据,计算各误差因素影响下的子母弹开舱高度散布。
基于以上思路,应用Matlab软件建立子母弹开舱高度仿真模型,使用龙格-库塔法求解作为二阶常系数非线性常微分方程组的6自由度外弹道方程组,时间步长取为0.001 s。
以某155 mm口径火炮为例进行计算,弹丸初速v0=897 m/s,初始射角θ0=50°。表1、表2分别列出了外弹道计算所用的弹丸特征参数和气动力参数。计算结果与参考值(弹丸设计计算书中的弹道模型计算结果)对比,如表3所列,其中:X表示射程;T表示飞行时间;Y表示最大弹道高;θc表示落角;vc表示落速。
表1 某155 mm口径火炮外弹道计算用参数
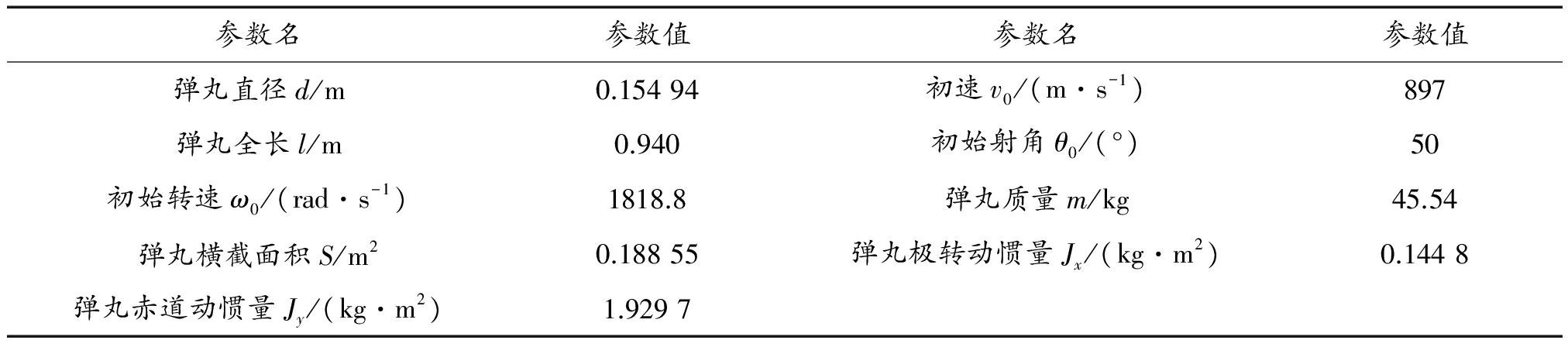
表2 某155 mm口径火炮6自由度弹道计算用气动力参数
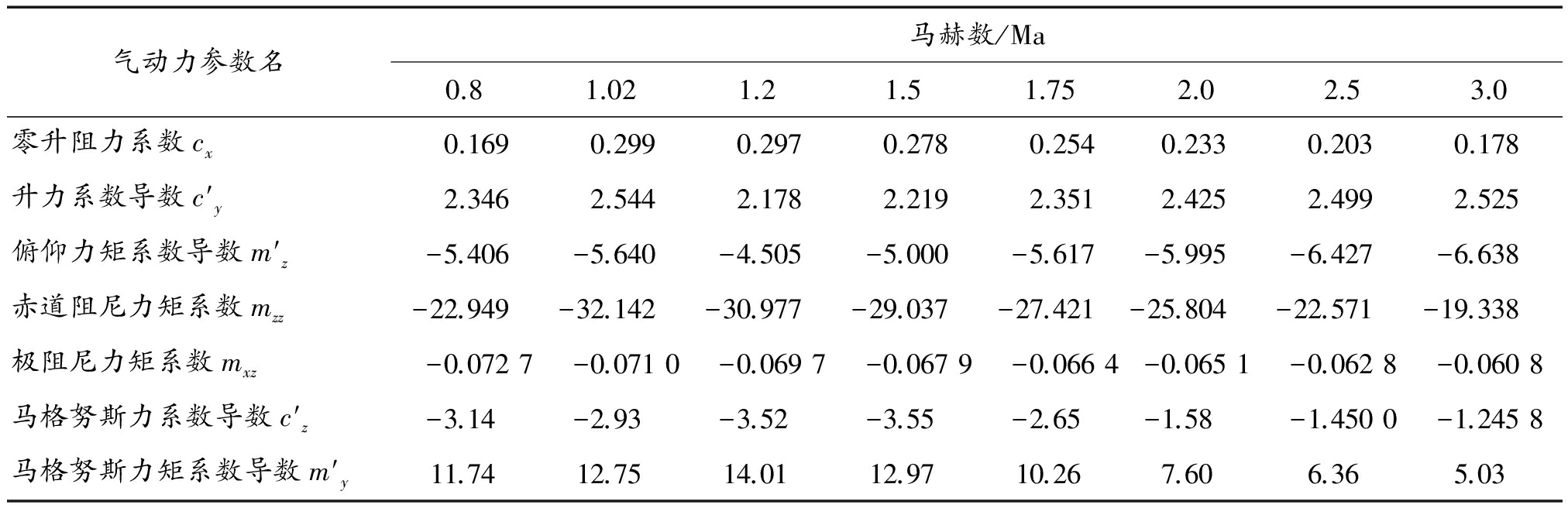
表3 外弹道诸元计算结果与参考值对比
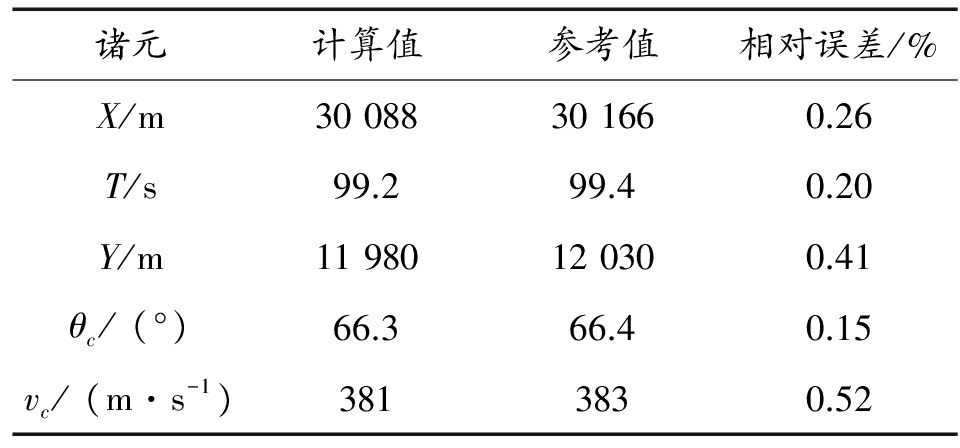
上述结果表明,该外弹道程序符合实际情况,时间步长选取恰当,结果具有足够的准确性和较高的可信度。
查阅相关资料,影响开舱高度的主要误差因素有[6]:初速误差Ev0、初始射角误差Eθ0、质量误差Em0、纵风EWx、定时误差Et。表4列出了各影响因素的误差分布规律及概率误差。
表4 某155 mm口径子母弹开舱高度影响因素概率误差

以某155 mm口径火炮为例,取上述影响因素概率误差,计算子母弹开舱高度。为便于研究,在此以外形和质量均比较接近的榴弹外弹道参数(包括气动力参数)近似代替子母弹的参数。
3 仿真结果及其分析
利用建立的开舱高度散布仿真模型,分别计算各误差因素影响下弹丸全射程(约50°射角)、最大射程2/3处(约17°射角)、最大射程1/2处(约11°射角)、最大射程1/3处(约6°射角)的开舱高度散布,结果如表5所列,其中H为预计开舱高度,t为对应的开舱时间;Eyαi表示单个误差因素影响下开舱高度中间误差;![]() 表示单个误差因素对开舱高度Ey的影响程度
表示单个误差因素对开舱高度Ey的影响程度![]()
由表5可看出,最大射程时,射角散布Eθ0对开舱高度Ey基本无影响,影响其开舱高度Ey的主要因素是初速散布Ev0(6.2%)、质量散布Em0(23.6%)、纵风散布EWx(63.5%)、时间散布Et(6.5%); 最大射程2/3处纵风散布EWx对开舱高度Ey的影响最大,其余各因素影响均较小;而最大射程1/2处和最大射程1/3处装定时间散布Et对开舱高度Ey的影响最大。
表5 不同射程下Ey各因素所占比值
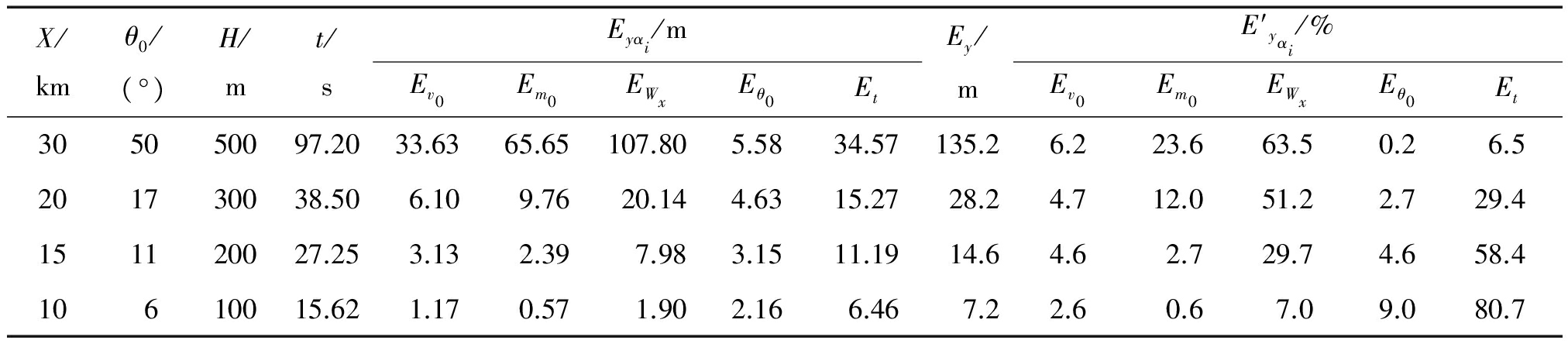
开舱点高度需大于4Ey才能以99.3%的概率保证子母弹在空中开舱,根据表5中的计算结果,最大射程时,高低散布Ey达135.2 m,而4Ey=540.8 m,因此此时为保证母弹在空中开舱且开舱后其内子弹正常作用,引信装定时间名义上应保证母弹最低开舱高度大于540.8+50(子弹姿态平稳和子弹引信解除保险所需最小降落高度)≈590 m。
文献[3-4]中取Ev0=0.2%v0、Eθ0=0.2mil、Ec=1.2%c、Et=0.1 s,运用误差合成方法得到155 mm口径火炮子母弹最大射程时高低散布Ey=130 m。与文献[3]、文献[4]中取相同的误差因素和数值,运用上述所建立仿真模型仿真得最大射程时高低散布Ey=138.4 m。在多考虑了纵风误差因素影响之后(但误差数值有所不同,初速误差偏小46%,与弹道系数误差相对应的弹丸质量误差偏小44%,初始射角误差和定时误差相同),本文仿真结果为Ey=135.2 m,在数值上与其基本一致。
4 结论
通过以上仿真计算,可得到如下结论:
1) 以最大射程、最大射程2/3的射程射击时,定时开舱高度高低散布受纵风影响大,其余各因素影响均较小。而对最大射程1/2、1/3的射程射击时,装定时间散布是影响定时开舱高度散布的主要因素;
2) 最大射程时,子母弹定时开舱高度高低散布Ey达135.2 m,开舱点高度需大于4Ey才能以99.3%的概率保证子母弹在空中开舱。因此为保证母弹在空中开舱,且开舱后其内子弹正常作用,引信装定时间名义上应保证母弹最低开舱高度大于590 m;
3) 同理,以最大射程2/3条件射击时,射击装定诸元中的名义最低开舱高度应大于4×28.2+50≈163 m;以最大射程1/2条件射击时,射击装定诸元中的名义最低开舱高度应大于4×14.6+50≈109 m;以最大射程1/3条件射击时,射击装定诸元中的名义最低开舱高度应大于4×7.2+50≈79 m;
4) 由于子母弹开舱点越高,子弹命中地面目标概率越低,所以从确保对目标命中和毁伤的角度考虑,配定时开舱引信的炮射子母弹不适合以最大射程攻击目标。
参考文献:
[1] 杨启仁.子母弹飞行动力学[M].北京:国防工业出版社,1999:1-9.
[2] 刘怡昕,王兆胜,钟宜兴.子母弹射击学与弹道学[M].北京:海潮出版社,2011:1-2.
[3] 王兆胜.火炮射击精度分析的模型与应用[M].北京:国防工业出版社,2013:116-119.
[4] 王兆胜.子母弹开舱高度高低散布研究[J].火炮发射与控制学报,2012(2):21-24.
[5] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2014:118-159.
[6] 郭锡福.火炮武器系统外弹道试验数据处理与分析[M].北京:国防工业出版社,2013:100-105.
[7] 王兆胜.远程炮武器系统射击精度研究与射击精度战技指标论证[D].南京:南京理工大学,2003:25-28.
[8] 王宝元.中大口径火炮射击密集度研究综述[J].火炮发射与控制学报,2015(2):82-86.
[9] 鲁玉祥,崔万善,徐坚,等.火炮最大射程地面密集度分析与预测[J].火炮发射与控制学报,2011(2):39-42.
[10] 钱明伟,王良明,郭锡福.火炮武器高原射击时的弹道特性研究[J].弹道学报,2009,21(4):21-25.
[11] 张浩,闻泉,王雨时,等.炮弹地面密集度性能与射程关系仿真研究[J].弹道学报,2016,28(1):56-59.
[12] 王国平,芮筱亭,陈卫东.多管武器系统密集度仿真技术[J].系统仿真学报,2004,16(5):963-966.
[13] 王锋,于存贵,马大为,等.舰载多功能火箭炮射击密集度仿真分析[J].弹箭与制导学报,2006,26(2):737-739.
[14] 姚志军,王国平,芮筱亭,等.简易控制远程多管火箭密集度仿真[J].系统仿真学报,2007,19(5):1127-1130.
