____________________________________________________________________________________________________________________________________
引用格式:张斐,周春桂,韩阳阳,等.玻璃射流对带壳装药冲击起爆的数值模拟[J].兵器装备工程学报,2017(12):86-89.
Citation formatZHANG Fei,ZHOU Chungui,HANG Yangyang, et al.Numerical Simulation on Glass Jet Initiating Explosive with Shell[J].Journal of Ordnance Equipment Engineering,2017(12):86-89.
____________________________________________________________________________________________________________________________________
作者简介:张斐,硕士研究生,主要从事高效毁伤战斗部设计及数值仿真研究。
____________________________________________________________________________________________________________________________________
玻璃射流对带壳装药冲击起爆的数值模拟
摘要:利用非线性动力学分析软件AUTODYN-2D对玻璃射流冲击起爆带壳B炸药进行了仿真研究,研究了不同装药参数对带壳装药冲击起爆的影响,实现了玻璃射流对带壳B炸药的穿而不爆。仿真结果表明,射流u2d值随着药型罩壁厚和锥角的增大逐渐减小,随着装药长径比的增大逐渐减小;玻璃射流冲击起爆带壳B炸药的u2d阀值均在15.543 mm3/μs2左右,说明玻璃射流可以用于反爆炸式反应装甲战斗部。
关键词:玻璃射流;带壳装药;起爆阀值;穿而不爆
中图分类号:TJ413 文献标识码:A 文章编号:2096-2304(2017)12-0086-04
Numerical Simulation on Glass Jet Initiating Explosive withShell
Abstract: In order to eliminate the interference of the reaction armor to the main jet, to achieve the glass jet on the shell with the penetration-but-not-detonated, numerical simulations by AUTODYN-2D software was carried out to emulate that glass jet initiate B explosive with shell. The effect of different charge parameters on the impact initiation of shell loading was studied, and the effect of glass jet on the shell B explosive was realized. The results indicate that the u2d decreases as the thickness and taper angle of liner increases,but the value of the jet u2d decreases as the charge-to-length ratio increases. The initiating value u2d of glass jet to B explosive with shell is about 15.543 mm3/μs2. The results show that glass jets can be used for Anti-Explosive Reaction Armor warhead.
Key words: glass jet; explosive with shell; initiating value; penetration-but-not-detonated
爆炸反应装甲(ERA)使传统的反坦克武器面临前所未有的挑战。目前串联战斗部是应用广泛且比较成熟的反ERA弹药 [1]。南京理工大学王健等的研究表明EFP可以对ERA实现穿而不爆,从而为主射流开辟道路[2]。但串联战斗部使用双引信, 增加了延时机构,若坦克在该时间间隔内发生横向偏移,前级装药所开辟的通道便失去了意义,且这种装药结构复杂导致破甲率和可靠性有所降低。射流能否引爆ERA夹层装药主要取决于透射冲击波的强度。低声抗材料聚合物形成的射流产生的压力比高声抗材料如铜射流产生的压力低得多。Cauchetier,J提出了一种结构更为紧凑的战斗部,用低密度射流侵彻ERA为后继主射流开辟通道[3]。A. Helte等人对这种战斗部的前级射流侵彻ERA进行了试验研究,发现氧化铝粉末和铝粉以及低密度材料药型罩形成的射流可以实现对反应装甲的穿而不爆[4]。国内中北大学王志军、董方栋等利用非线性动力学分析软件AUTODYN-2D对特氟龙、尼龙等低密度材料射流冲击起爆带壳B炸药进行了仿真研究,并分别实现了高速下对带壳B炸药的穿而不爆[5]。
本文用采用非线性动力学分析软件AUTODYN-2D,对玻璃射流侵彻ERA进行了数值模拟,得出了浮法玻璃射流对带壳装药冲击起爆判据,以期对反ERA战斗部设计提供一定理论依据。
1 数值仿真模型
1.1 有限元模型及算法
聚能装药中炸药爆炸以及药型罩的压垮均属于大变形问题,因此主装药、药型罩均采用Euler算法;带壳炸药面板、夹层炸药和背板采用Lagrange算法,带壳装药与聚能装药、药型罩以及空气进行流固耦合,在欧拉域采用中心加密的渐变网格,并在空气边界上添加“Flow_out”边界条件来消除边界效应。聚能战斗部有限元模型如图1所示。装药口径为36 mm,

图1 有限元模型
装药高度为36 mm,药型罩锥角为70°,且药型罩内端圆角半径为3 mm,药型罩外部圆角半径为药型罩内端半径与壁厚之和,壁厚为3 mm。带壳装药的面板、夹层炸药、背板厚度分别为2 mm、4 mm、2 mm[6],在夹层炸药中设置6个高斯点,以便观察夹层炸药各点的压力。
1.2 材料模型及参数
药型罩材料为浮法玻璃,用Polynomial状态方程和Johnson-Holmquist强度模型来描述其本构关系。面板和背板材料为30CrMnSi,用Linear状态方程和Johnson Cook强度模型来描述本构关系。主装药和被装药均为军用B炸药,分别用JWL和Lee-Tarver状态方程来描述,所用材料参数均来自AUTODYN程序材料库。
2 装药引爆判据
射流侵彻反应装甲时,射流头部撞击前面板产生的冲击波,射流冲击波压缩装药,装药受到比能
E=put
(1)
式中: p为冲击波后压力; u为波后质点速度; t为冲击波作用时间。冲击波作用时间为:
t=dj/2c
(2)
式中: dj为射流直径; c为声速。冲击波后压力P可以表示为
p=ρ0uD
(3)
式中: ρ0为装药密度; D为冲击波传播速度。故装药受到比能为:
E=ρ0u2Dd/(2c)
(4)
由于u与冲击波强度有关,冲击波强度又与射流速度有关,因此有:
u=Avj
(5)
此外,声速与冲击波速度关系为:
c=BD
(6)
因此有:
E=![]() ×v2dj=K1v2dj
×v2dj=K1v2dj
v2dj=![]() =K=const
=K=const
其中K为常数,是装药起爆判据,当达到临界值时,装药会被引爆。对于不同材料的射流,K值不同[7]。
对于聚能装药射流的密度对起爆阀值的影响, Held则定义了u2d,它对应于坑底的驻点压力,其中u是高能炸药中的开坑速度,对于流体动力学的侵彻过程,开坑速度用Bernoulli方程给出
故
K=u2d=![]() d
d
对于B炸药,K=23 mm3/μs2。其中ρH和ρp分别是炸药及射流的密度。因此,本文将采用这一起爆判据。
3 数值仿真模拟结果及分析
3.1 射流成型过程
浮法玻璃射流在不同时刻的成型状态如图2所示。从图2可知,低密度药型罩在主装药爆轰的情况下,可以形成高速射流。浮法玻璃药型罩在被压垮闭合过程中具有射流成型各阶段的的典型特征。主装药起爆约8 μs后,爆轰产物将以很高的压力冲量作用于药型罩顶部,引起药型罩顶部的高速变形,药型罩开始被压垮、并在轴线上闭合,在中心发生相互碰撞、挤压,13 μs时已完成汇聚,形成高速侵彻体。由于药型罩顶部的有效装药量大,因而压垮速度大,形成的射流速度高;而在药型罩底部,有效装药量少,压垮速度和相应的射流速度较低。由于头尾速度差的存在,侵彻体在运动中逐渐拉伸,出现颈缩现象,当运动到一定炸高时射流被拉断。
3.2 数值仿真结果分析
本文对装药口径为36 mm,采用不同锥角及壁厚的玻璃药型罩冲击起爆位于3倍口径炸高的带壳装药进行了数值模拟。分析讨论了射流的u2d随不同药型罩壁厚δ,不同药型罩锥角2α,不同装药长径比λ的变化情况。
聚能装药的装药长径比λ为0.9、药型罩锥角2α为90°时,浮法玻璃药型罩形成的射流的u2d值随药型罩壁厚δ变化曲线如图3所示,夹层炸药的冲击起爆结果如表1所示。由图3和表1可知:当长径比λ和药型罩的锥角2α一定时,浮法玻璃药型罩形成的射流的u2d值随着药型罩壁厚δ的增大而逐渐减少,夹层装药的状态由爆炸逐渐过渡到未爆,即其冲击起爆能力在逐渐递减,而穿而不爆的能力在逐渐递增。
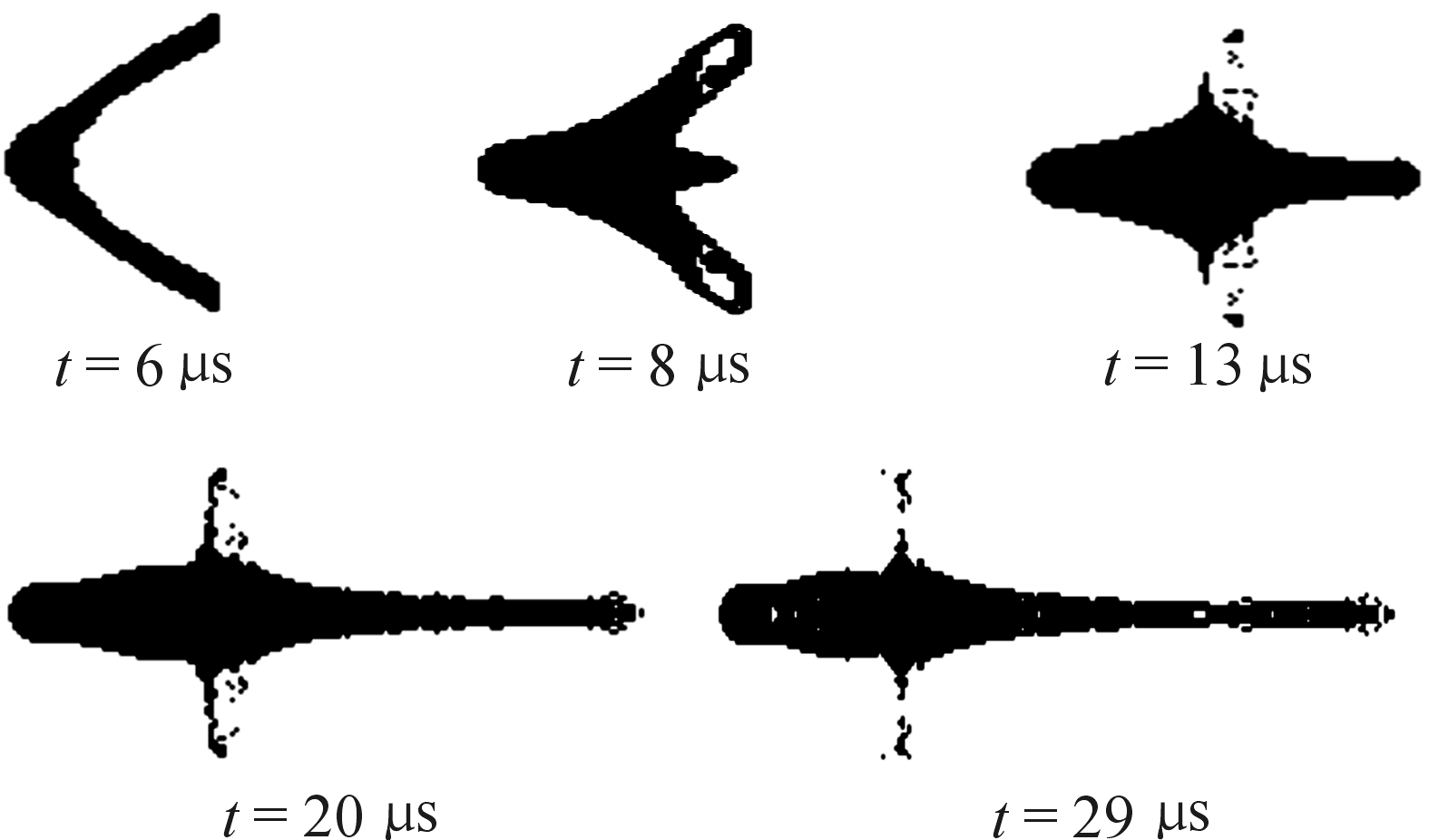
图2 射流成型过程
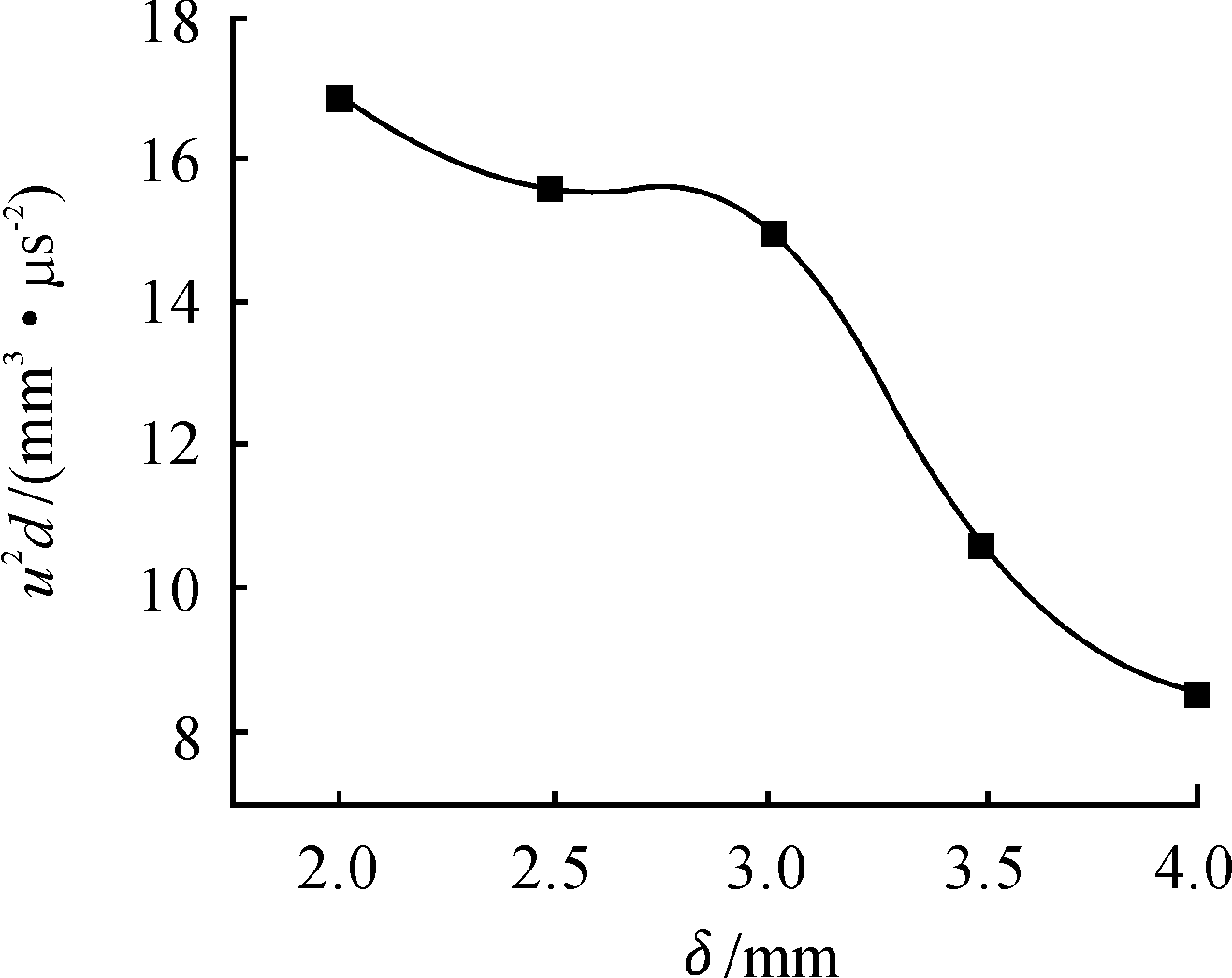
图3 u2d值随壁厚δ的变化曲线
表1 λ=0.9,2α=90°时,夹层炸药冲击起爆结果

聚能装药的装药长径比λ为0.9、药型罩壁厚δ为3 mm时,浮法玻璃药型罩形成的射流的u2d值随药型罩锥角2α的变化曲线如图4所示,夹层炸药的冲击起爆结果如表2所示。由图4和表2可知:当长径比λ和药型罩的壁厚δ一定时,随着药型罩锥角2α的增大,射流的着靶速度在减小,起爆系数K=u2d也在减小,冲击起爆能力在逐渐递增,而穿而不爆的能力在逐渐递减。
药型罩壁厚δ为3 mm,锥角2α为90°时,浮法玻璃药型罩形成的射流的u2d值随装药长径比λ的变化曲线如图5所示,夹层炸药的冲击起爆结果如表3所示。由图5和表3可知:当药型罩的壁厚δ和锥角2α一定时,随着装药长径比λ的增大,射流的着靶速度在增大,夹层装药的状态由未爆逐渐过渡到爆炸,即其冲击起爆能力在逐渐增强,而穿而不爆的能力在逐渐减弱。
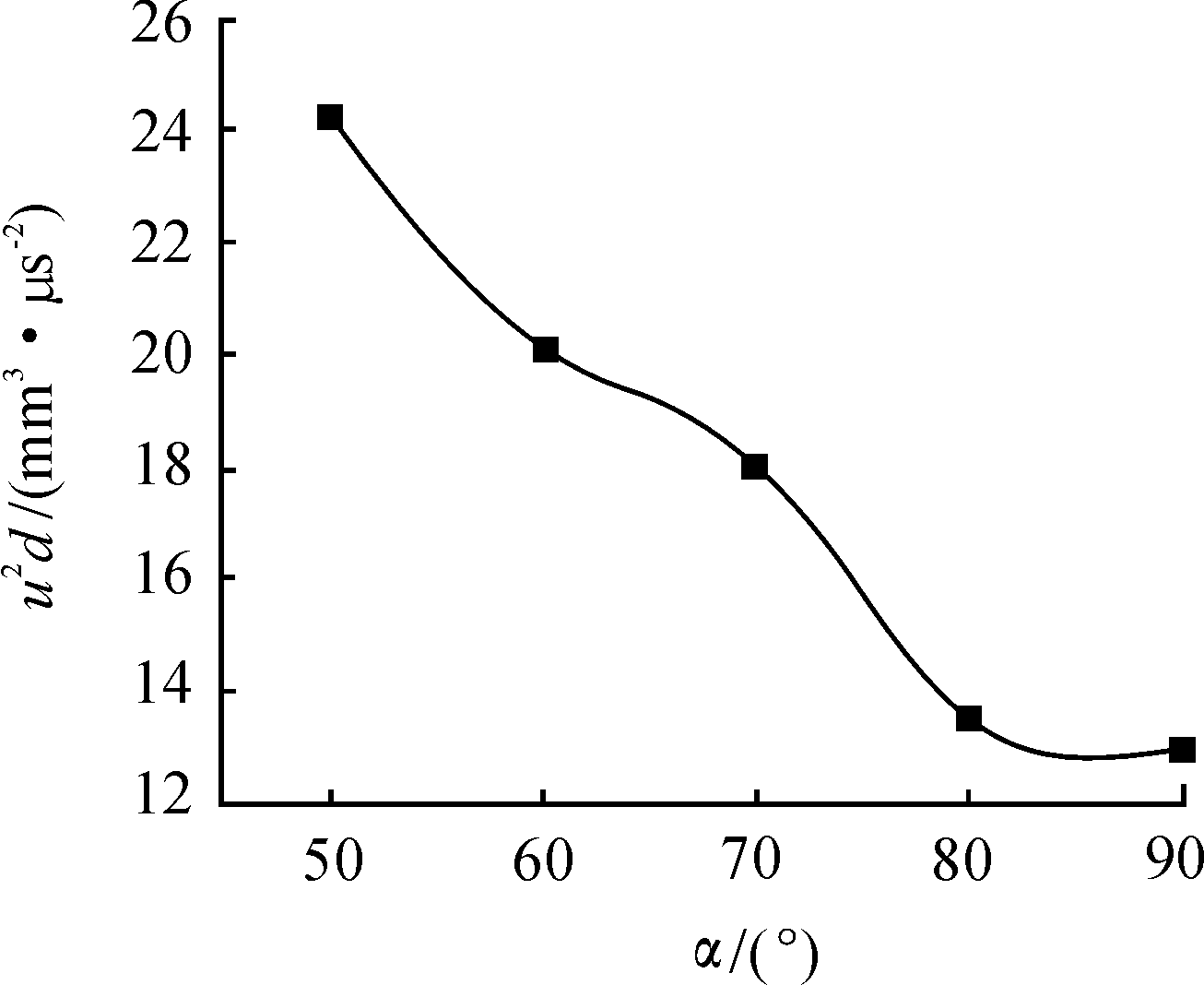
图4 u2d值随锥角2α的变化曲线
表2 λ=0.9,δ=3 mm时,夹层炸药冲击起爆结果

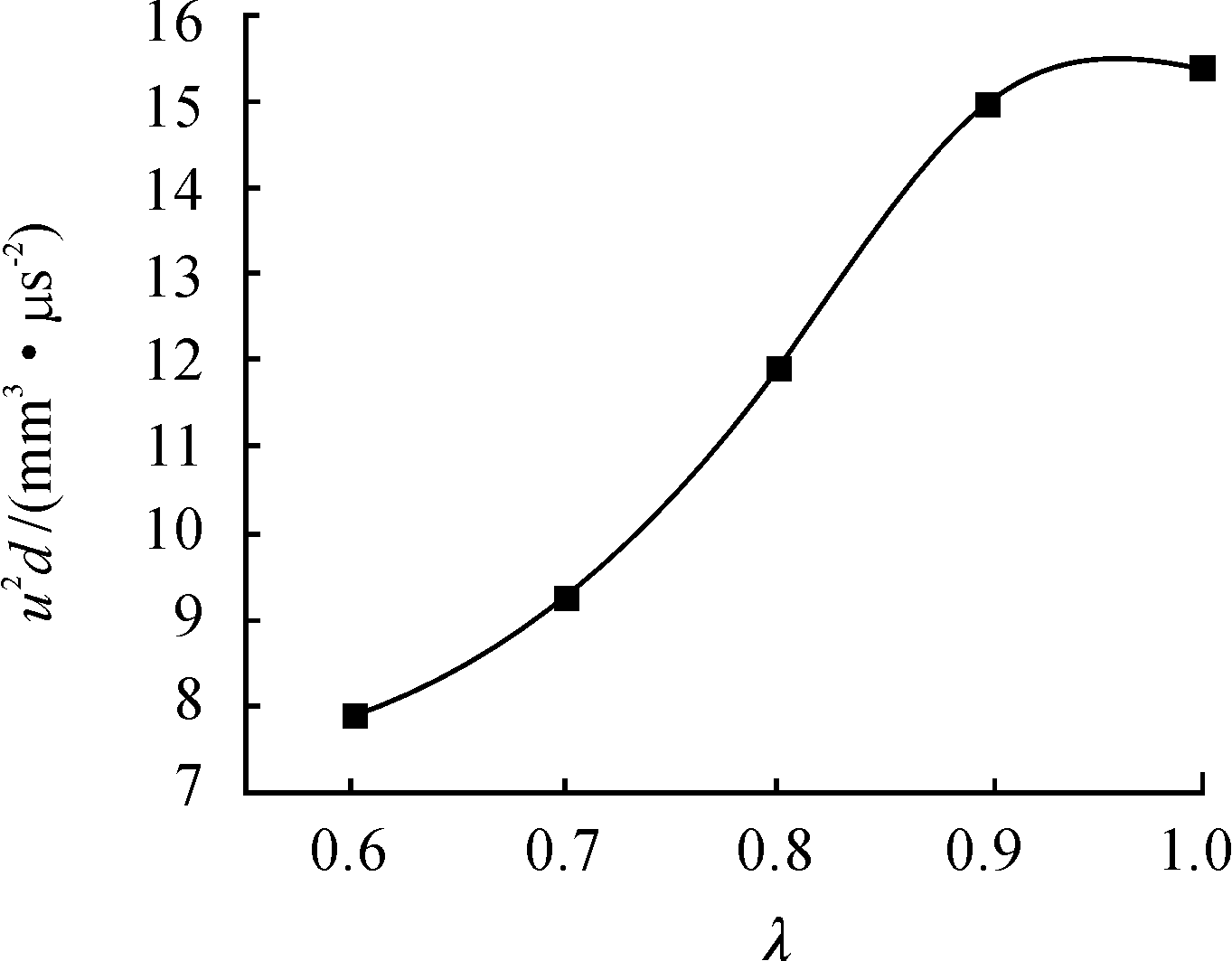
图5 u2d值随装药长径比λ的变化曲线
表3 2α=90°,δ=3 mm时,夹层炸药冲击起爆结果

3.3 夹层装药分析
夹层装药反应度云图如图6,图6从左到右B炸药状态依次为未爆、爆燃和爆炸。图7为夹层装药爆燃时,观测点的压力随时间的变化曲线。从图7可以看出夹层装药为B炸药时,其爆燃时的最大压力为5.48GPa,而B炸药的临界起爆压力为5.63 GPa,仿真结果与试验结果值的误差为2.66%。
计算B炸药的起爆阈值时采用Held判据,在公式u2d=![]() d中,由于浮法玻璃药型罩在被压垮形成射流后,其密度随着闭合拉伸程度的增大而减小,经仿真计算,密度在1.34~1.4 g/cm3之间,故在计算中射流密度应为侵彻带壳装药前的射流密度。经计算得到浮法玻璃药型罩形成的射流冲击引爆带壳B炸药的u2d阀值K=15.543 mm3/μs2。
d中,由于浮法玻璃药型罩在被压垮形成射流后,其密度随着闭合拉伸程度的增大而减小,经仿真计算,密度在1.34~1.4 g/cm3之间,故在计算中射流密度应为侵彻带壳装药前的射流密度。经计算得到浮法玻璃药型罩形成的射流冲击引爆带壳B炸药的u2d阀值K=15.543 mm3/μs2。
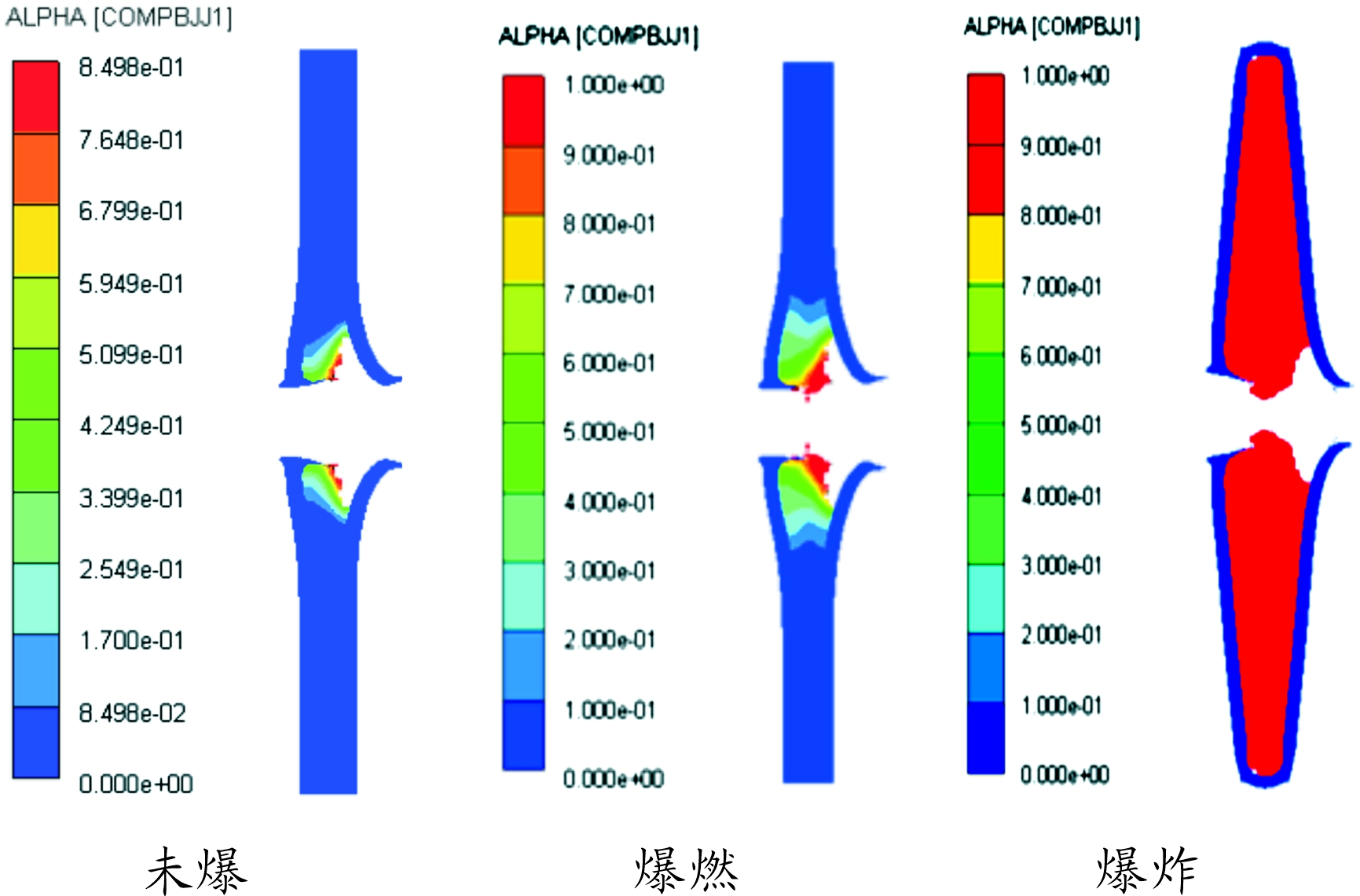
图6 夹层装药反应度云图
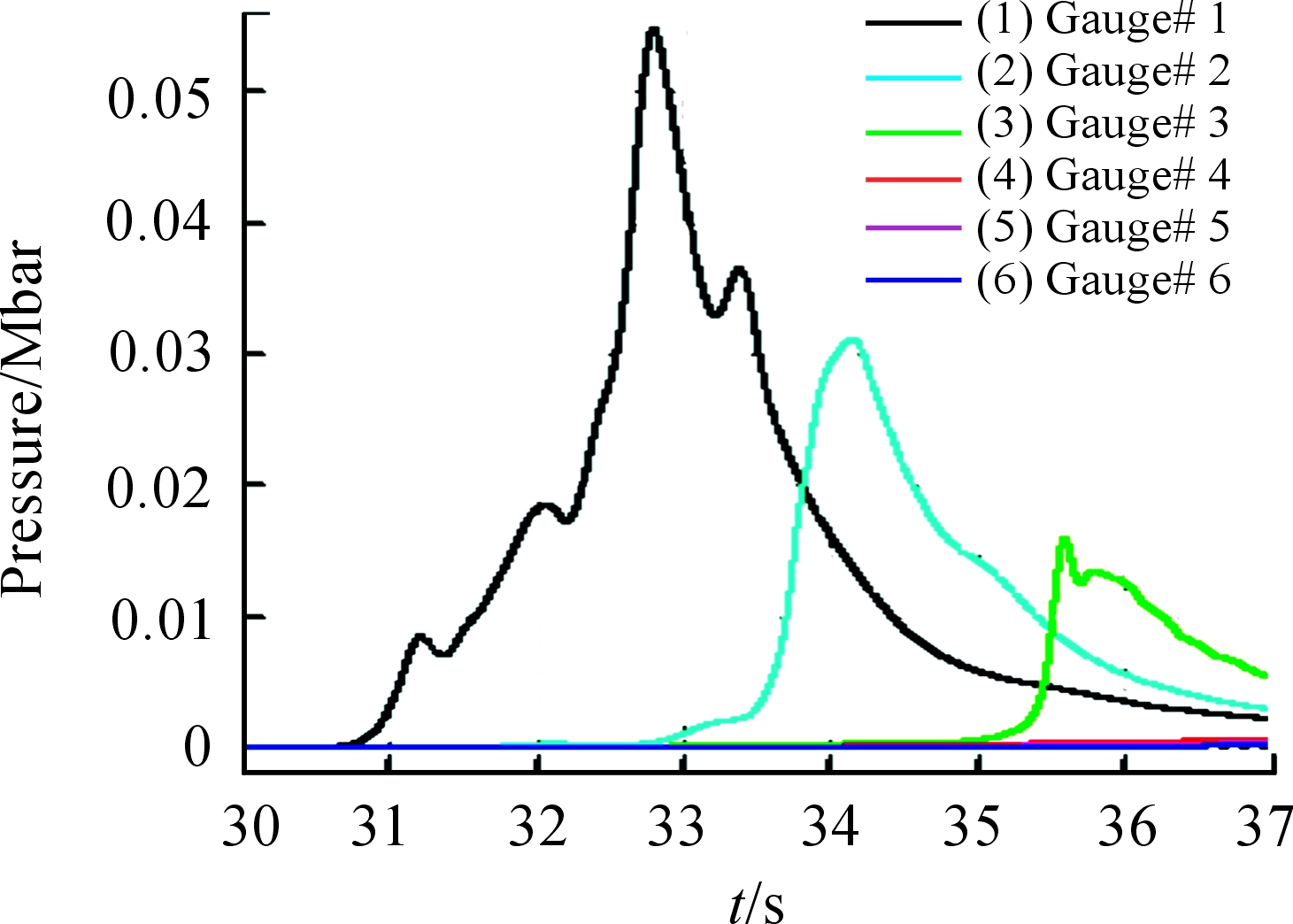
图7 夹层装药观测点压力变化曲线
4 结论
本文通过对浮法玻璃射流对夹层炸药冲击起爆的数值仿真,得到以下结论:
1) 浮法玻璃射流冲击引爆ERA的u2d阀值为15.543 mm3/μs2,说明了数值仿真研究射流冲击起爆的可行性;
2) 在一定条件下,浮法玻璃射流冲击引爆ERA的u2d阈值与药型罩壁厚和锥角成正相关,与装药长径比成负相关,但其起爆阀值基本不变。
3) 浮法玻璃射流可对ERA实现穿而不爆,可以作为穿破型串联战斗部的前级装药,为后级主射流开辟通道,可应用于反ERA的战斗部中。
参考文献:
[1] 郎明群,徐学华.多级串联聚能装药隔爆时间的计算与测试[J].南京理工大学学报,2002,26(6):625-628.
[2] 王健,曹红根,周箭隆. EFP侵彻爆炸反应装甲过程研究[J].南京理工大学学报,2008,32(1):9-12.
[3] CAUCHETIER J. Explosive Device with a Hollow Charge,Designed for Penetrating Armor Protected by Active Primary Armor[P]. US Patent 5394804.1995-7-3.
[4] Non-inttiating Precursor Charge Technology Against Era[C]// 26th International Sympositum on Ballistics Miami,FL,2011:12-16.
[5] 董方栋,王志军,尹建平,等.低密度射流冲击带壳装药起爆阈值的数值仿真[J].兵器材料科学与工程,2013,36(4):15-19.
[6] 刘宏伟.爆炸反应装甲飞板变形及干扰射流模型[D]南京:南京理工大学.2007.
[7] HELD M. Discussion of the experiment findings from the initiation of covered but unconfined high explosive charge with shaped charge jets[J].Propellants, Explosive, Pyrotechnics, 1987, 12: 167-174.
