一种用于柔性飞机风洞静气动弹性试验的数据处理方法
静气动弹性表征了系统气动载荷和结构弹性之间的耦合作用,对飞行器的气动性能与飞行安全有着重要影响。风洞试验作为一种可靠的飞行器载荷评估方法,在飞行器的研制过程中有着重要的意义[1-2]。随着新材料等领域的快速发展,为获得较好的升阻特性,越来越多的复合材料被用到了大展弦比飞机的机翼中[3],这也导致这类飞机机翼在气动载荷作用下会产生较大形变,且非线性特性明显[4],由此带来的风洞试验安全问题也越来越严峻。因此,大展弦比飞机的静气动弹性效应问题日益被重视,成为当前飞行器气动弹性专业领域的研究热点之一[5]。
美国通过F/A-18A飞机的主动气动弹性翼(Active Aeroelastic Wing,AAW)风洞试验,尝试利用机翼的气动弹性效应达到更好的颤振抑制和飞行控制性能[6]。Carlson[7]通过对某大展弦比后掠机翼进行低速静气动弹性风洞试验,研究了机翼的变形量、气动力和气动力矩的变化规律。杨超等[8]通过曲面涡格法与有限元的耦合对某柔性飞机飞行载荷进行了计算。付志超等[9]通过MD Nastran软件对某大展弦比柔性飞机结构动力学特性参数进行了计算。
为得到某柔性飞机飞行载荷准确数据,本文对某柔性飞机全模进行风洞试验,并通过地面加载试验及相应数据处理方法对大展弦比机翼应变-载荷数据进行快速估测,提高风洞试验效率与安全性。最后通过对比天平信号的处理结果,验证这种试验方法的准确度。
1 试验说明
1.1 试验模型与设备
此次试验采用了翼身组合体整机模型,如图1所示。机身是刚性的,只提供整流作用;机头与机尾部分分别由树脂材料与铝合金材料加工而成。在试验中,模型通过圆柱铰链与支架相连,机翼则通过螺钉与机身相连。
加工两套厚度为6 mm与7 mm的变截面大展弦比柔性机翼,称作1号机翼与2号机翼,分别用于在试验中正负攻角的工况。


图1 整机模型图(风洞试验中)
1.2 试验流程
整个试验分为地面加载试验与风洞试验两部分,其中地面加载试验是通过向机翼两侧悬挂的砝码架增加砝码的方式分别向两套机翼施加载荷,待机翼稳定后,通过应变-全桥电路测量机翼的变形,得到两套机翼在不同载荷下的应变值。同时,通过处理地面加载试验数据得到两套机翼应变-载荷拟合方程。
在随后的风洞试验部分,对中国航天空气动力技术研究院FD-09风洞[10]中安装有不同机翼的模型分别固定攻角3.77°和-7.33°,依次增加风速进行吹风,同时通过DASP数字采集系统对机翼的应变量进行采集。在一个车次的吹风结束后,通过本文改进的k均值聚类方法对此车次中采集到的大量离散点进行快速处理,从而得到此车次中不同风速下机翼的应变量。将不同风速下机翼的应变量插值入地面试验得到的机翼应变-载荷拟合方程中,即可得到不同风速下机翼所受载荷。
对比机翼载荷-风速曲线与机翼的安全极限,可为后续车次试验的风速控制提供指导。整个试验流程如图2所示。
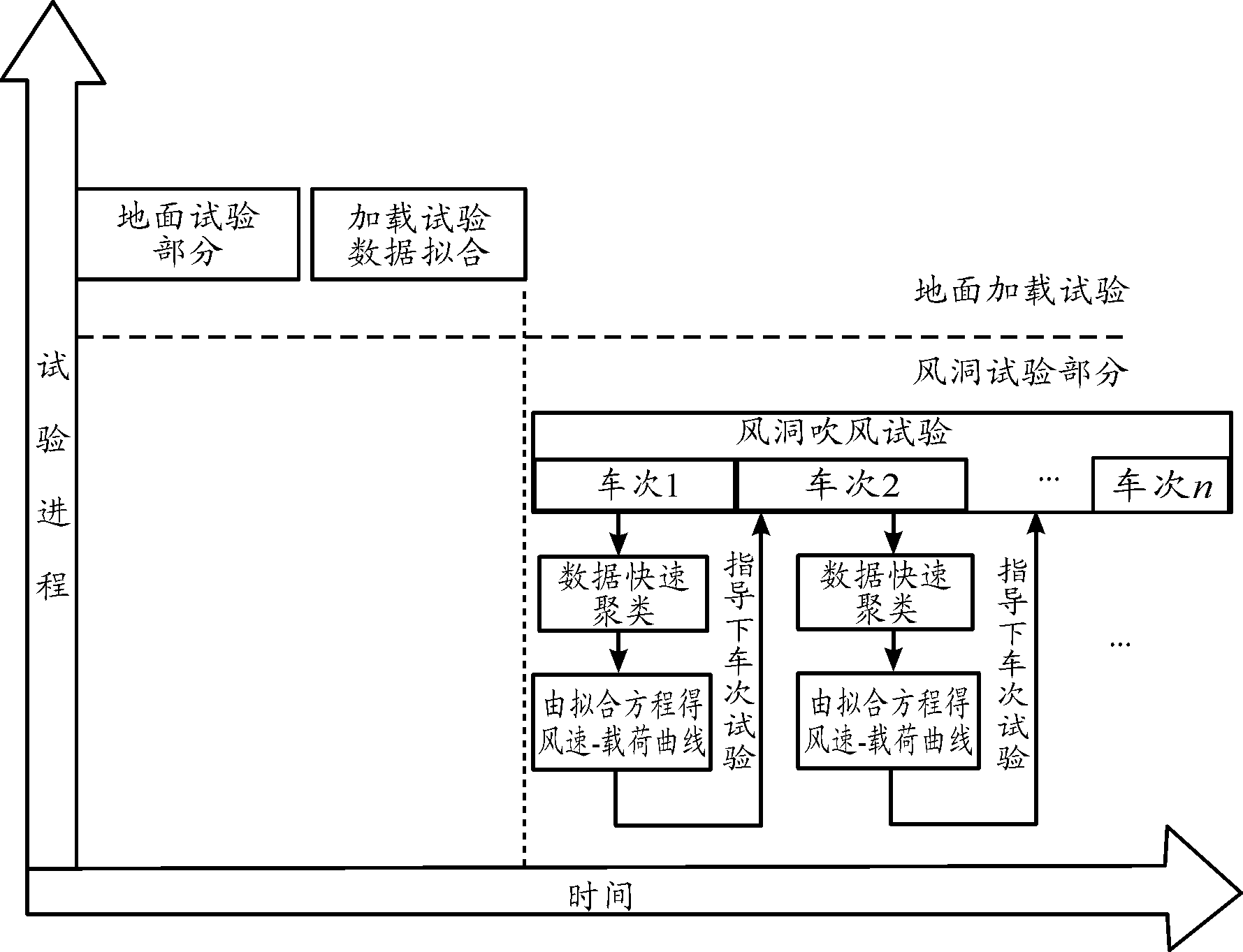

图2 试验流程设计
2 数据处理方法
为更准确地刻画机翼的变形信息,此试验中设计数字采样频率51.2 Hz,因此原有风洞数据处理方法难以实现数据快速处理。本文通过数据聚类思想,设计了一种基于k均值聚类法的迭代式聚类方法,并结合地面试验拟合方程,用于风洞试验中快速得到机翼在不同风速下的载荷情况,数据处理的基本思想如图3所示。
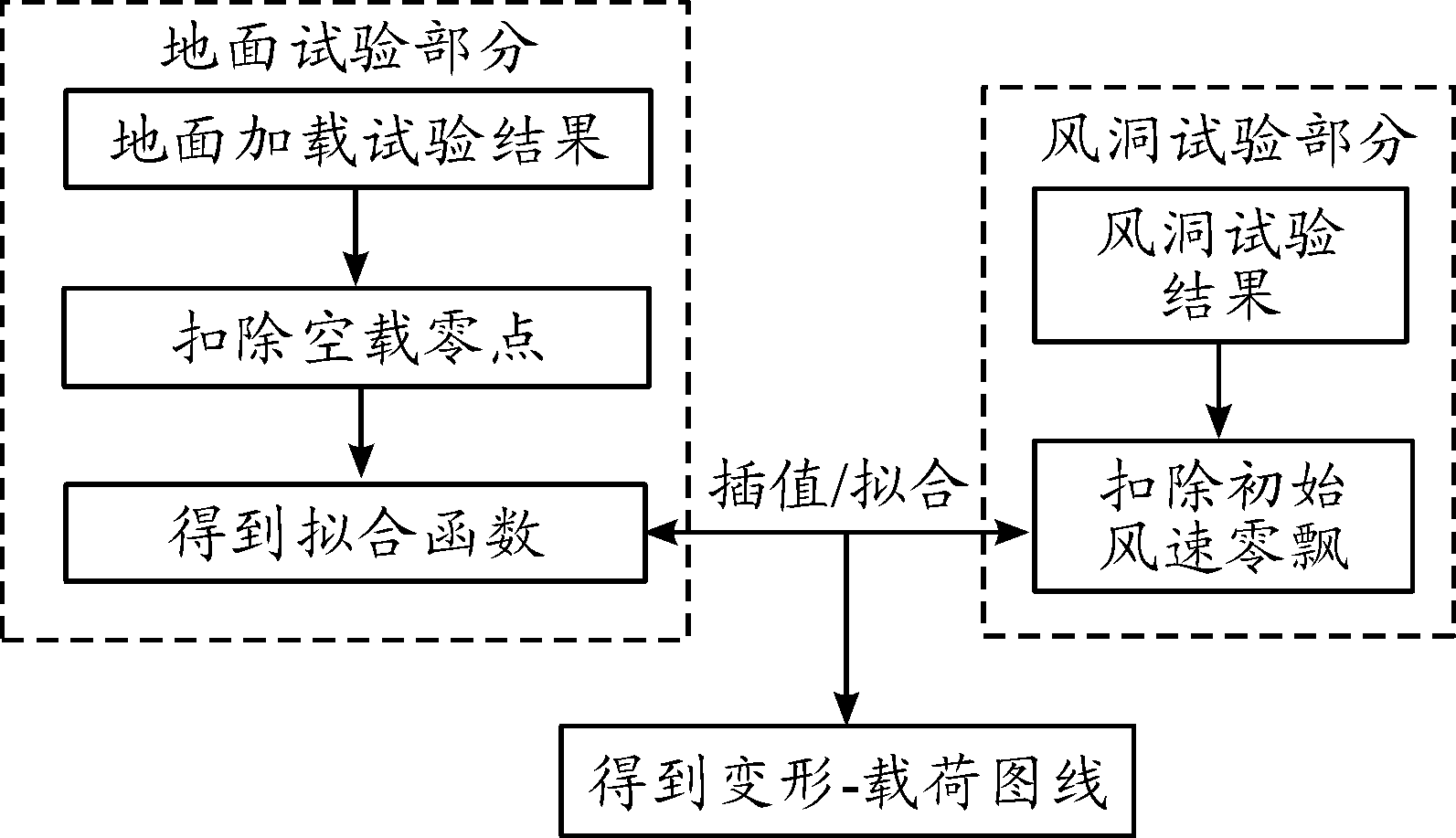

图3 数据处理流程示意图
2.1 地面数据拟合
通过地面加载试验可以得到不同载荷下机翼的应变,如图4和图5所示。
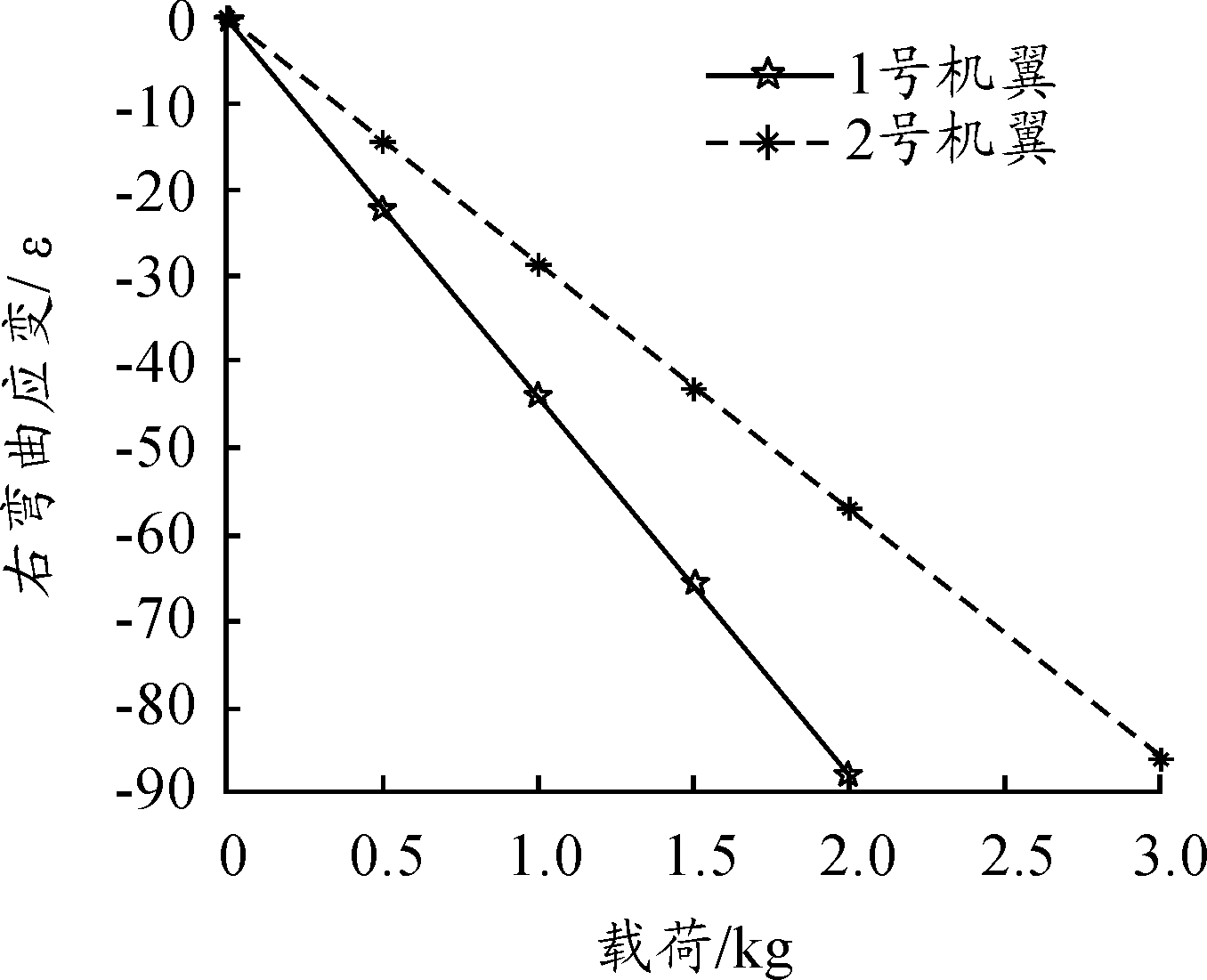
图4 地面试验左侧机翼应变


图5 地面试验右侧机翼应变
由地面加载试验结果可发现,随着载荷的增加,两套机翼均产生较大的弯曲应变,且较厚的2号机翼具有较大的弯曲刚度;而对于同一机翼,在相同载荷下左右弯曲应变增量基本一致。
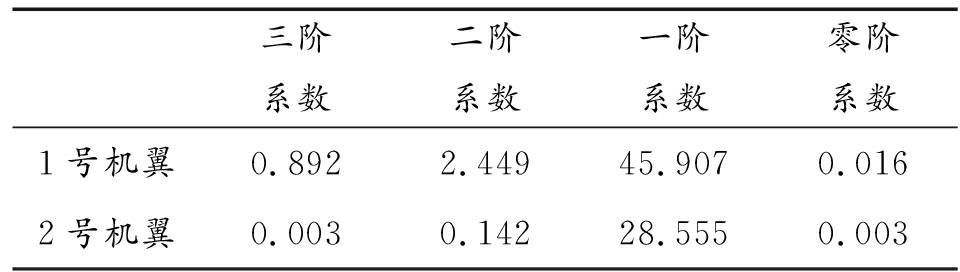
结合材料力学思想,通过高次多项式对两套机翼的应变—载荷关系进行拟合[11]。通过试验发现三次多项式对地面加载试验数据有很好的拟合效果。综合考虑,采用三次多项式对两套机翼的应变—载荷关系进行拟合,拟合结果如表1。
表1 两套机翼应变—载荷拟合系数

2.2 风洞数据处理
在风洞试验中,风速按照阶梯形式逐步上升,数字采集系统同时对各传感器所监测的物理信号进行采集,但由于数据采集频率高,机翼弯曲过程中微振动明显,快速稳定的数据处理方法至关重要。本文在传统k均值聚类方法的基础上,结合本次试验数据特点发展出一种聚类数目已定的k均值聚类方法[12]。
2.2.1 传统k均值聚类方法
传统的k均值聚类方法用于对D维空间RD中的n个数据X={x1,x2,…xn} 进行聚类,将其归为C1,C2,…,Ck共k大类,且满足k大类之间不重不漏。每个类的类心为其几何中心mj。
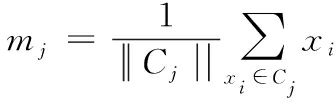
(1)
式(1)中,||Cj||表示第j类中样本的个数。
而每个样本到不同类之间的距离,根据其到每个类类心的欧式距离d定义[12]
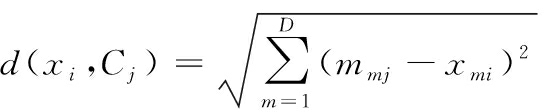
(2)
对于聚类效果,由总体离散度F进行评价,在满足实际问题边界的前提下,总体离散度越小,表明类间差异越大而类内差异越小[13-14]。
![]()
(3)
综上所述,传统k均值聚类方法步骤如下:
1) 对样本数据,随机选择k个初始类心m01,m02,…,m0k,取初始总体离散度F0=+∞;
2) 根据样本到初始类心的距离将其归入到距离最近的类中,得k个大类C1,C2,…,Ck;
3) 重新计算每个类的类心,得到归类后类心m1,m2,…,mk,同时计算此时总体离散度F;
4) 计算样本到类心的距离,并将其归入聚类最近的类中,得k个大类![]()
5) 重新计算每个类的类心,得到归类后类心![]() 同时计算此时总体离散度F′;
同时计算此时总体离散度F′;
6) 将此时总体离散程度与上一步进行对比,若F′=F则聚类结束,否则由步骤4)开始重新进行迭代,直至前后两次聚类总体离散度一致。
2.2.2 本文改进后k均值聚类方法
柔性飞机机翼在风洞试验阶梯变化的风速中主要呈现出阶梯状的变形特性,机翼的大柔性导致机翼在变形过程中微振动明显。同时,相比数据采集频率,风洞风速变化过程缓慢,常用数据处理方法难以判别和剔除风速变化过程中所采集的机翼变形信号。为减小这些误差的影响,在传统k均值聚类方法的迭代过程中加入人工控制过程。
首先,在初始化阶段将传统方法中随机确定的类心更改为由风洞控制系统给出的风速变化时刻的数据采集点。
其次,在k均值聚类方法的每一步迭代过程中加入均值滤波操作。设置聚类效果的度量值α和均值过滤控制参数β,当迭代前后总体离散度满足![]() 时,即认为此次迭代效果强烈,对迭代后每一个类的内部元素进行过滤,剔除区间B以外的元素,其中B=[(1-β)mj(1+β)mj]。
时,即认为此次迭代效果强烈,对迭代后每一个类的内部元素进行过滤,剔除区间B以外的元素,其中B=[(1-β)mj(1+β)mj]。
最后,为防止出现局部最优化,设置过滤控制参数β为迭代次数p的减函数,防止B区间随着迭代次数的增加扩大。
在引入以上人工控制过程后,针对此次柔性飞机风洞静气弹试验的改进k均值聚类方法流程如图6所示。


图6 改进k均值聚类流程
在试验过程中,通过上述改进后的k均值聚类方法可以在某车次试验结束后快速得到机翼在不同时刻下的应变,再通过对地面试验拟合方程的插值就可以得出不同风速下机翼所受载荷,为后续车次的风速控制提供指导。
3 试验结果分析
通过改进的k均值聚类方法,可以快速得到两套机翼在不同风速下的机翼应变值与天平所测整机升力,如图7~图9所示。通过观察数据处理结果可发现:随着风速增加,固定正攻角3.77°的1号机翼应变量逐渐正向增大而固定负攻角-7.33°的2号机翼应变值逐渐负向增大,两套机翼的弯曲应变规律均与地面加载现象一致。
由于模型支持轴承的横向间隙会使模型产生偏航角误差,同时应变片安装精度也会产生零飘误差,因而对于同一机翼,在相同风速下左右两侧产生的弯曲应变会有差异。
通过风洞试验中所测得机翼的应变对地面拟合方程的插值,可以得到两套机翼在不同风速下所受载荷。为使对比结果更加清晰,在数据处理中对天平所测整机升力与应变插值所得机翼载荷均扣除初始风速(15 m/s)下的载荷,所得结果如图10所示。
由图10可发现,随着风速增加两套机翼所受载荷与天平所测得模型升力变化规律一致;改进k均值聚类方法得到的机翼应变对地面试验拟合函数进行插值可以快速计算柔性机翼载荷,综合误差小于8%。且误差主要由模型加工的非对称性、模型平尾攻角安装偏差、模型支撑轴横向间隙所造成。
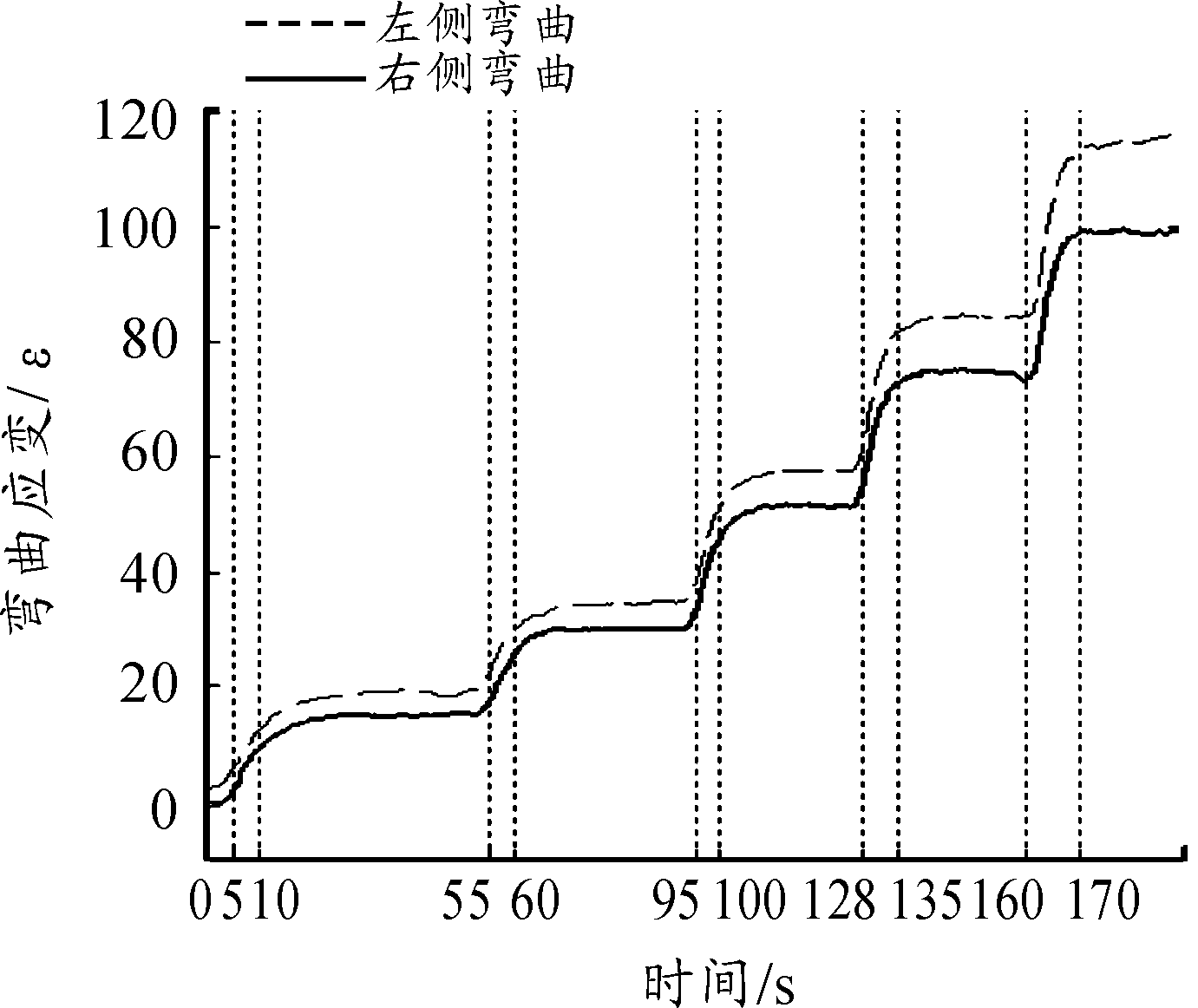
图7 1号机翼风洞
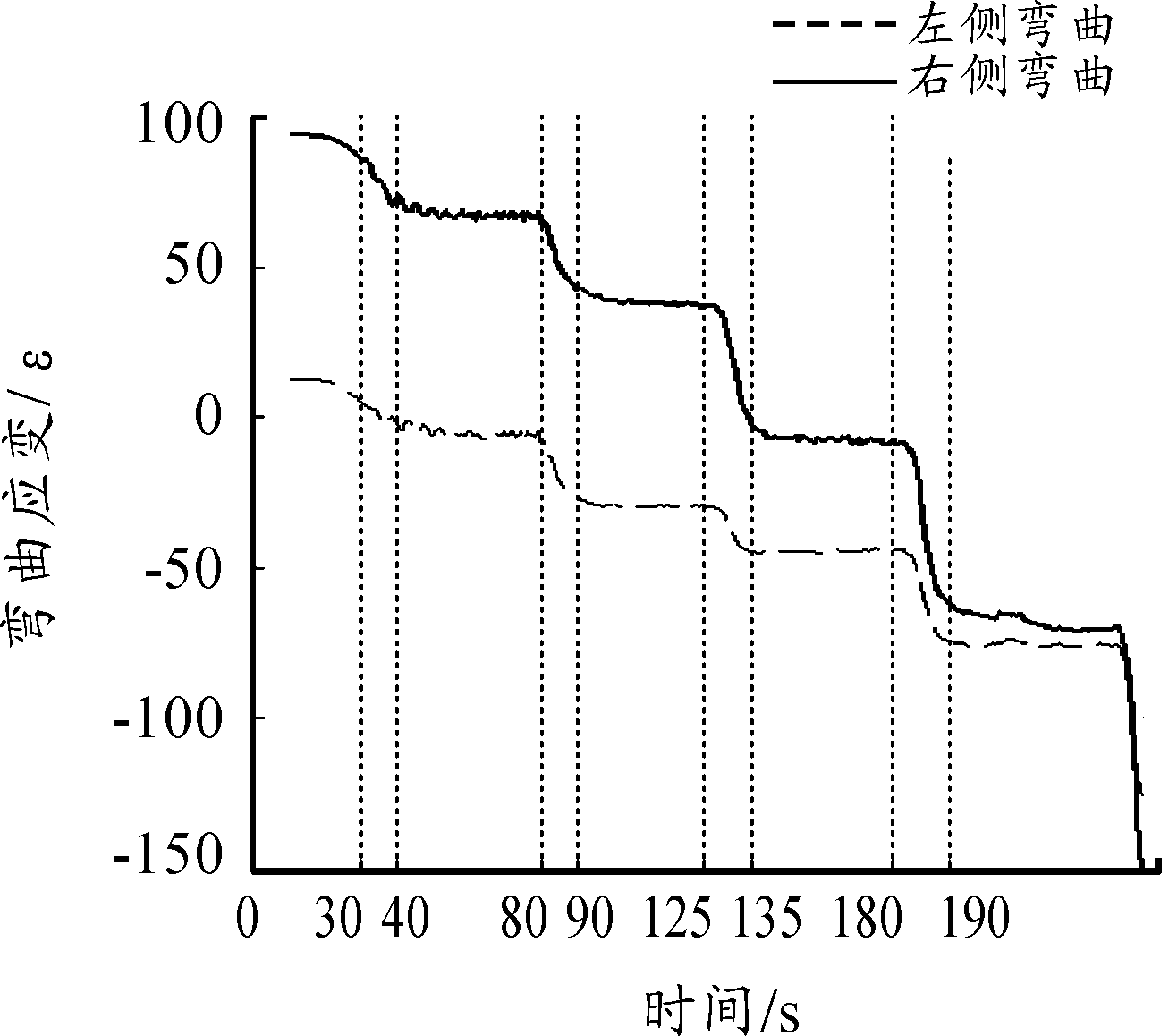
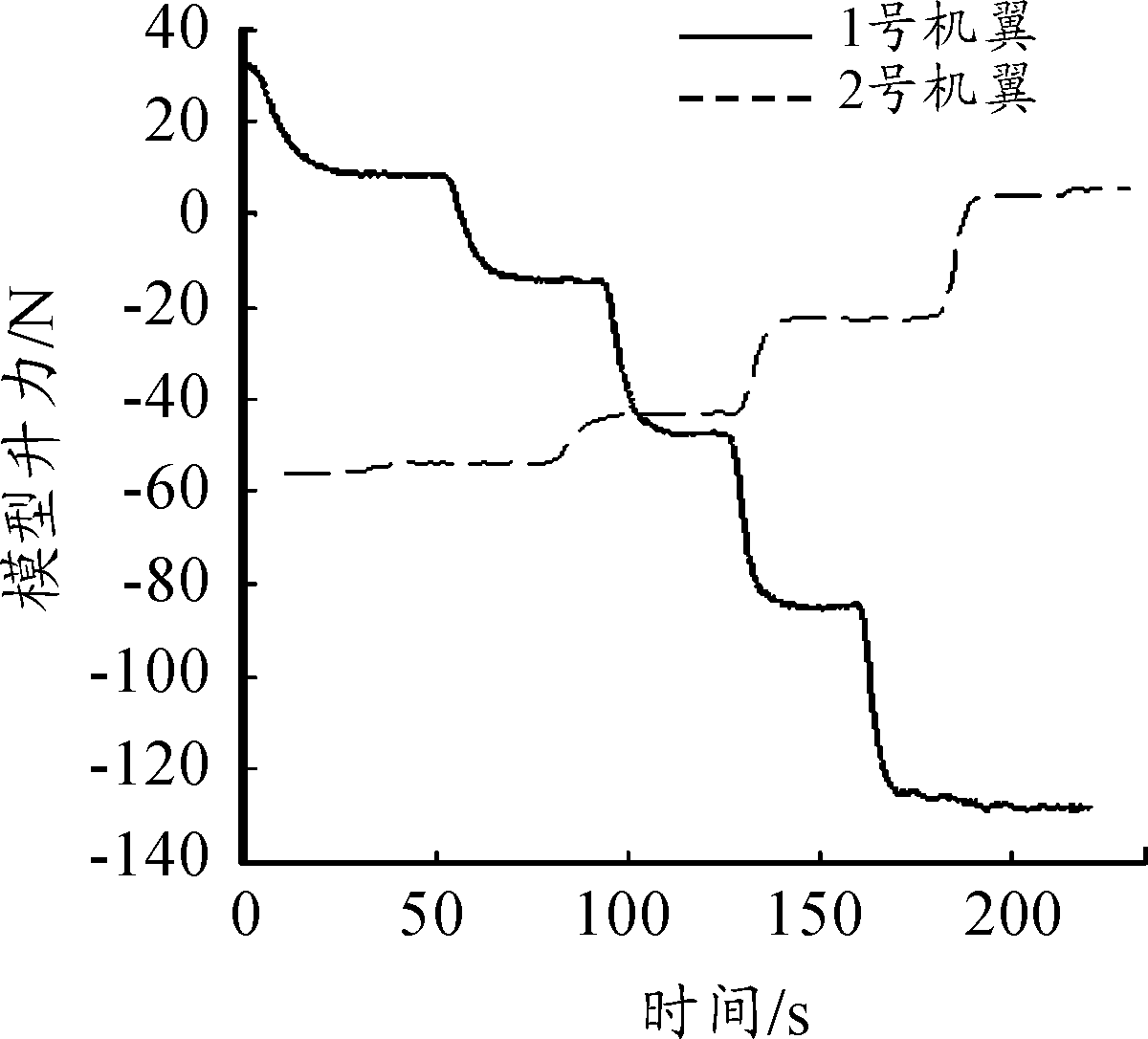
图8 2号机翼风洞
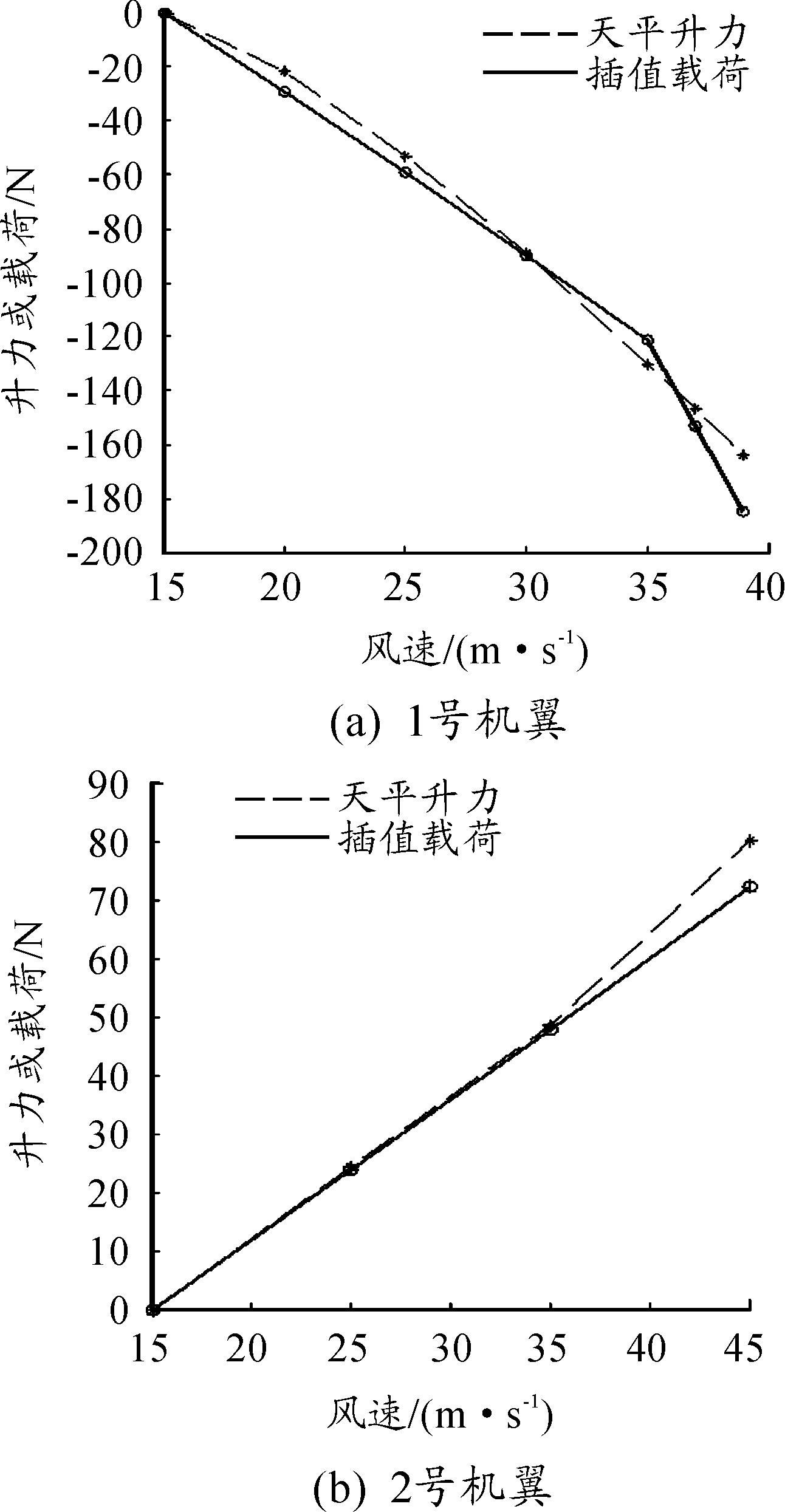

图9 两套机翼天平

图10 两套机翼地面-风洞试验插值载荷与天平升力
4 结论
对某大展弦比柔性飞机静气动弹性效应进行了风洞试验研究,得到了两套机翼的静气动弹性特性。同时本文在地面加载试验基础上通过改进k均值聚类方法对风洞试验数据进行快速处理,发展了一种机翼载荷的快速计算方法,并通过对比风洞天平数据对这种方法进行了验证。通过与风洞天平数据的对比,这种机翼载荷快速计算方法所得到结果有较高的准确性。这种机翼载荷快速计算方法为后续车次的试验提供了指导,提高了风洞试验的安全性与效率。
[1] 杨超.飞行器气动弹性原理[M].北京:北京航空航天大学出版社,2016.
[2] 季辰;刘子强;李锋.钝前缘梯形翼高超声速风洞颤振试验[J].气体物理,2018(1):54-63.
[3] 邱波.现代军用飞机[J].四川兵工学报,2007(4):7-10.
[4] 谢长川,胡锐,王斐,等.大展弦比柔性机翼气动弹性风洞模型设计与试验验证[J].航空学报,2016,33(11):249-256.
[5] 钱卫,张桂江,刘钟坤.大展弦比机翼低速静气动弹性模型的设计、制作和风洞试验[J].实验流体力学,2013,27(3):93-97.
[6] ANDERSEN G,FORSTER E,KOLONAY R,et al.Mutiple control surface utilization in active aeroelastic wing tehnology[J].Journal of Aircraft,1997,34(4):552-557.
[7] CARLSSON M.Control surface response of a blended wing body aeroelastic wind tunnel model[R].AIAA Paper 2003-0450,2003.
[8] 杨超,王立波,谢长川,等.大变形飞机配平与飞行载荷分析方法[J].中国科学:技术科学,2012,42(10):552-557.
[9] 付志超,仲维国,陈志平,等.大展弦比柔性机翼的结构动力学试验研究[J].航空学报,2013,34(9):2177-2183.
[10] 贾毅,蔡国华.FD-09风洞发展历程及在风工程与工业空气动力学方面的应用和前景[C]//2010年中国结构风工程研究30周年纪念大会文集.北京:中国土木工程学会,2011.
[11] 范钦珊.材料力学[M].北京:高等教育出版社,2005.
[12] 朱建宇.k均值算法研究及其应用[D].大连:大连理工大学,2013.
[13] 逄玉俊,柳明,李元.k均值聚类分析在过程改进中的应用[J].华中科技大学学报(自然科学版),2009,37(S1):245-247.
[14] 张红云,李萍萍.一种基于层次聚类的k均值算法研究[J].微计算机信息,2010,26(4/3):228-229 232.
