基于结构方程模型的卫星应用体系评估研究
Research on Satellite Application System Assessment Based on SEM
针对当前卫星应用体系评估方法受主观因素影响较大,缺乏足够的说服力,本文结合结构方程模型(Structural Equation Modeling,SEM)[1],提出了一种更加客观的卫星应用体系评估方法。该方法建立在卫星应用能力体系、卫星应用装备体系和卫星应用技术体系聚合关系基础上,分析了内在的固有属性,可以为制定卫星应用体系的发展规划提供决策支持[2]。
1 结构方程模型基本原理
结构方程模型于20世纪70年代初由Karl.Joreskog提出,是应用线性方程系统表示显变量与潜变量之间,以及潜变量之间关系的一种统计方法[3]。其基本思想是:如果某些变量不能直接观测(潜变量),但是可以通过一些能够直接观测的变量(显变量)进行表征,即可以建立两者之间的映射关系,通过分析显变量,来发掘潜变量之间的隐藏关系[4-5]。
结构方程模型中,依据变量的观测属性及影响关系,可以划分为显变量、潜变量、外生变量和内生变量四种类型[6]。其中,显变量是能够直接观察或直接测量获得,获得的数据可以转化为量化数据,通常也称观测变量、测量变量和外显变量;潜变量是不可直接测量或无法直接观察得到的,只能以间接的方式推论出来,通常也称无法观察的变量、建构变量[7];外生变量是不受其他任何变量影响但对于其他变量存在影响的变量,通常也称自变量、上游变量;内生变量是受到任何一个其他变量影响的变量,通常也称因变量、上游变量[3]。结构方程模型示意图如图1。
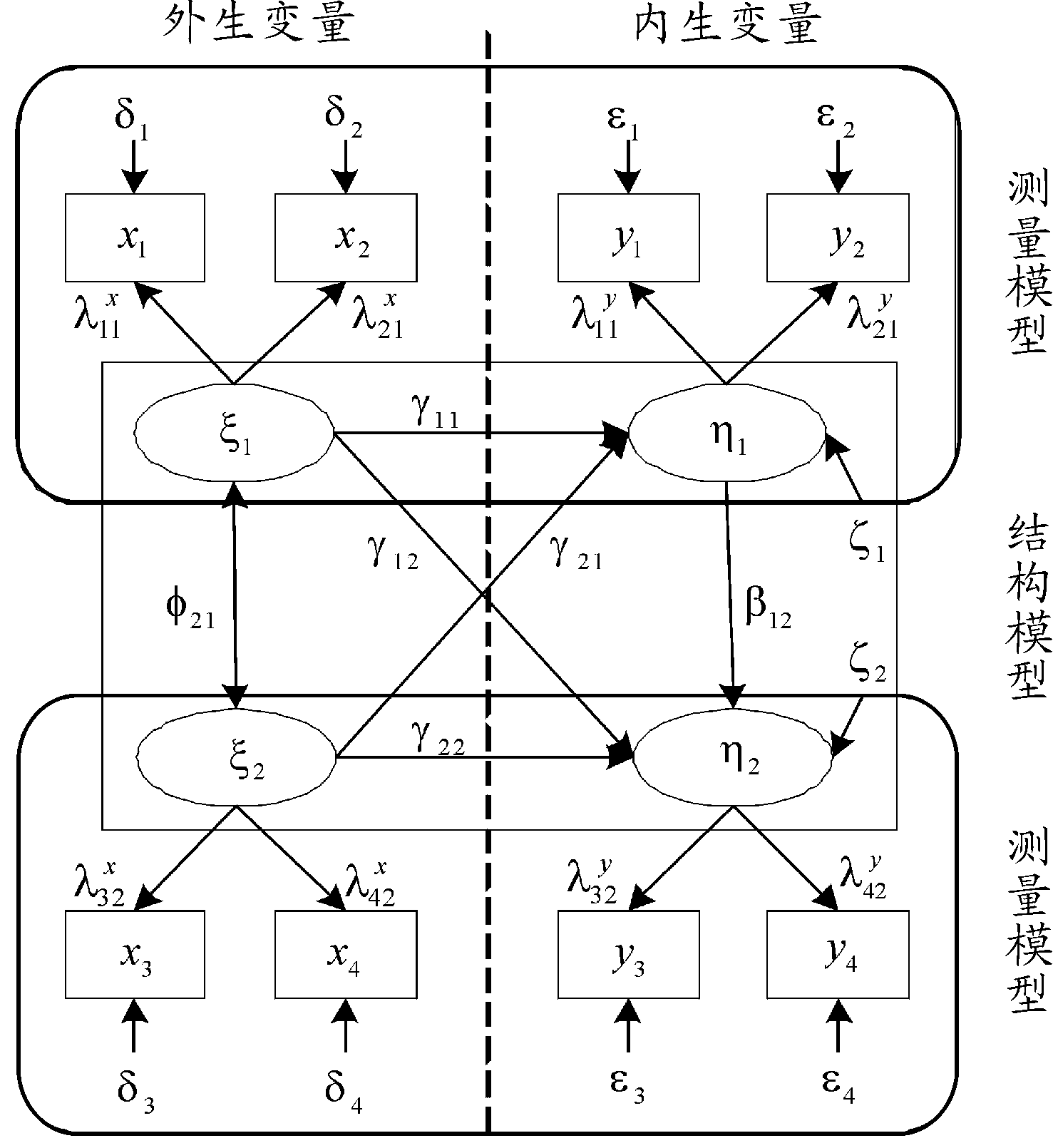
图1 结构方程模型示意图
在测量模型中,ξ1和ξ2是两个外生潜变量,η2是内生潜变量,η1是中介潜变量,既受到外生潜变量ξ1和ξ2的作用,又作用于内生潜变量η2。x1和x2、x3和x4分别是ξ1和ξ2的外生显变量,y1和y2是中介潜变量η1的中介显变量,y3和y4是内生潜变量η2的内生显变量。δ1、δ2、δ3、δ4分别是外生显变量x1、x2、x3、x4的残差项,ε1和ε2是中介显变量y1和y2的残差项,ε3和ε4是内生显变量y3和y4的残差项![]() 和
和![]() 和
和![]() 反映外生潜变量ξ1和ξ2对外生显变量x1和x2、x3和x4的负载,
反映外生潜变量ξ1和ξ2对外生显变量x1和x2、x3和x4的负载,![]() 和
和![]() 反映中介潜变量η1对中介显变量y1和y2的负载,
反映中介潜变量η1对中介显变量y1和y2的负载,![]() 和
和![]() 反映内生潜变量η2对内生显变量y3和y4的负载。
反映内生潜变量η2对内生显变量y3和y4的负载。
在结构模型中,γ11和γ21是外生潜变量ξ1和ξ2对中介潜变量η1的结构系数,反映外生潜变量ξ1和ξ2和中介潜变量η1之间的结构关系,γ12和γ22是外生潜变量ξ1和ξ2对内生潜变量η2的结构系数,反映外生潜变量ξ1和ξ2和内生潜变量η2之间的结构关系。φ21是外生潜变量ξ1和ξ2之间的结构系数,反映外生潜变量ξ1和ξ2之间的结构关系,β21是外因潜变量η1对内因潜变量η2的结构系数,反映外因潜变量η1和内因潜变量η2之间的结构关系。ζ1和ζ2是中介潜变量η1和内生潜变量η2的残差项。
在明确变量的基础上,结构方程模型通过测量模型和结构模型来表示。
测量方程模型:X=ΛXξ+δ,Y=ΛYη+ε
结构方程模型:η=Bη+Γξ+ζ
上述结构方程模型中所用的符号及定义如表1所示。
表1 结构方程模型符号及定义

矩阵方程式中的变量与路径图中变量的对应关系为
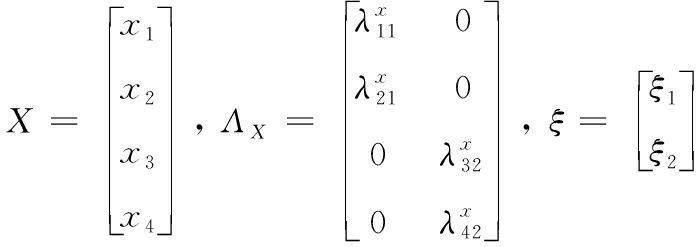
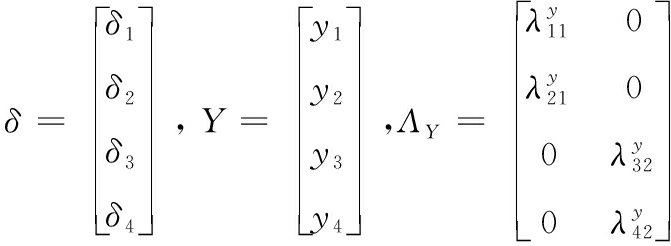
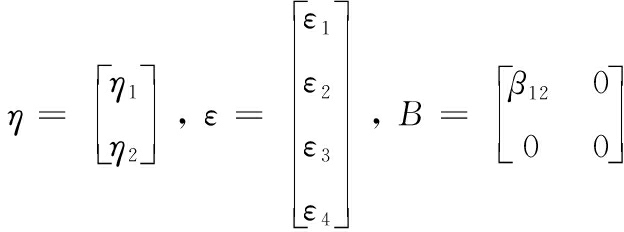
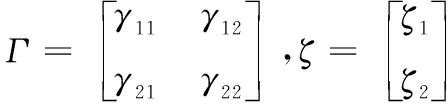
测量模型和结构模型设定之后,结构方程模型分析的基本框架也搭建完毕,此时,初步构建的理论模型所包含的所有关系都可以通过结构方程模型路径图或结构方程模型方程式的形式显现。目前结构方程模型的构件、参数的估计以及评估修正的过程通常可以通过LISREL、AMOS、SAS[8-9]等分析软件实现,本文主要使用AMOS软件进行分析。
2 卫星应用体系评估过程
基于结构方程模型的卫星应用体系评估的基本过程是从卫星应用技术体系、卫星应用装备体系和卫星应用能力体系出发,对卫星应用体系进行评估。在获取卫星应用技术体系、卫星应用装备体系和卫星应用能力体系样本数据基础上,建立从卫星应用技术映射到卫星应用装备,再从卫星应用装备映射到卫星应用能力的解析模型,其中建立卫星应用技术与卫星应用装备,以及卫星应用装备与卫星应用能力之间的解析模型是该方法的核心。建模步骤如下:
1) 提取作战方案的关键要素。根据基本作战想定,分析作战方案,提取构成作战方案的卫星应用体系关键要素指标。
2) 构建卫星应用体系评估指标体系。以卫星应用关系为基础,对卫星应用体系指标进行细化分解,建立卫星应用体系的评估指标体系。
3) 获取卫星应用技术体系、卫星应用装备体系和卫星应用能力体系的样本数据。如果条件允许,可以使用真实数据作为样本数据;在难以获得真实数据时,使用专家打分法、调查问卷法获取样本数据。
4) 推导解析模型。建立卫星应用体系评估的结构方程模型,进行参数估计,推导卫星应用技术体系指标映射到卫星应用装备体系指标,以及卫星应用装备体系指标映射到卫星应用能力体系指标的解析模型。
5) 评估卫星应用体系。根据解析模型对卫星应用体系的影响要素进行分析。
基于结构方程模型的卫星应用体系评估过程如图2所示。
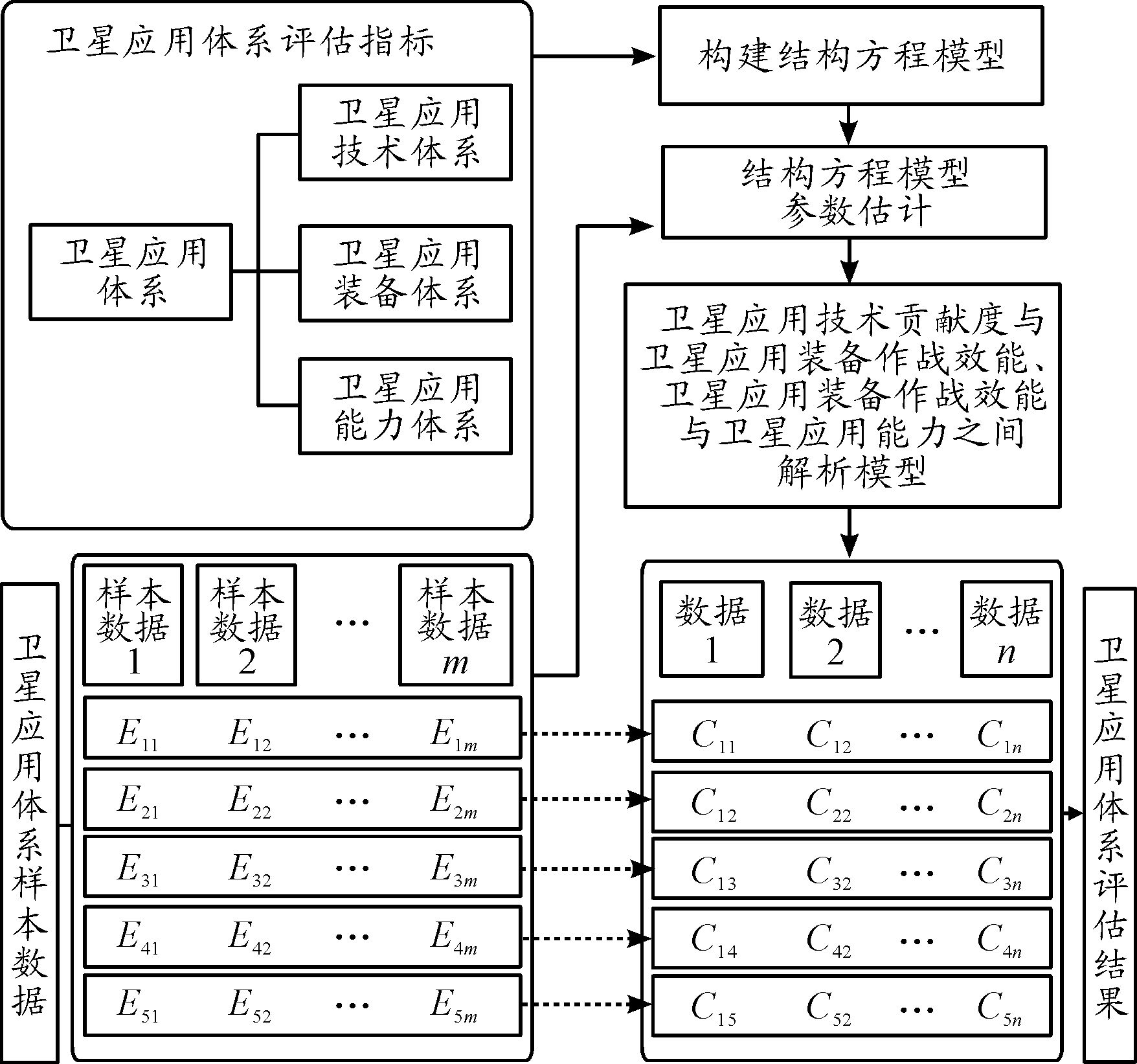
图2 基于结构方程模型的卫星应用体系评估过程
3 实例分析
现以某次远程精确打击为例,对卫星应用体系评估进行验证。远程精确打击作战模拟,如图3所示。
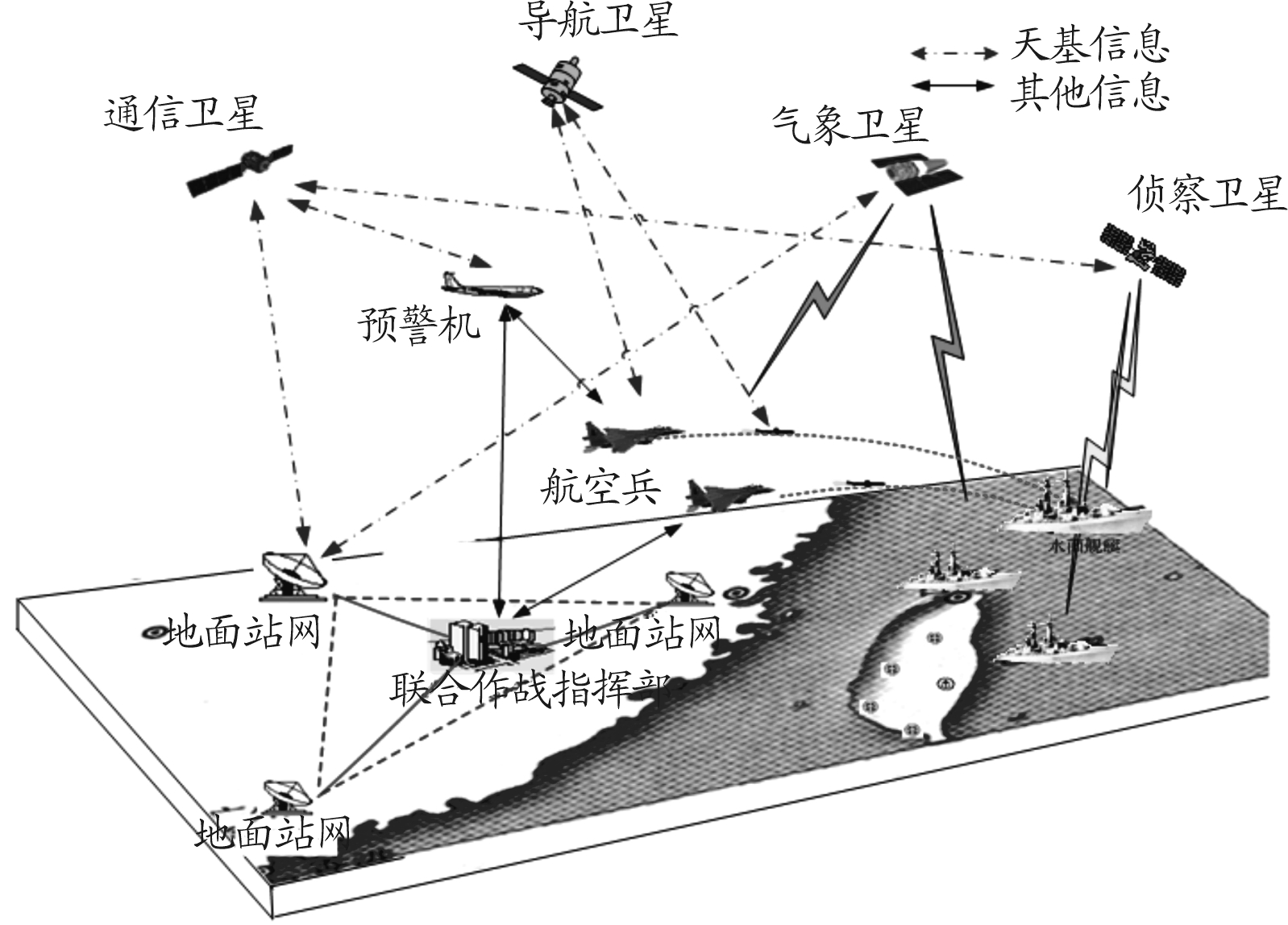
图3 远程精确打击作战模拟
3.1 作战想定与卫星应用方案设计
基本想定:蓝方出动水面舰艇编队欲攻击红方重要军事目标,红方侦察卫星发现蓝方舰艇编队的活动迹象,并对目标周围海域进行搜索,意图在蓝方舰艇编队发动攻击前,出动海军航空兵对其进行攻击,消灭威胁[10-11]。
卫星应用方案设计:红方依靠海洋环境监测卫星和气象卫星探测蓝方舰艇编队水域的水文气象情况,判断战场环境是否满足实施远程精确打击,根据侦察卫星和海洋监视卫星实时监视蓝方睡眠舰艇编队的航向、航速,红方联合作战指挥部通过卫星通信下达作战命令到海军航空兵部队,海航战斗机依靠太空导航定位系统到达目标打击区域范围后,搜索蓝方舰艇编队,根据舰艇类型确定攻击武器的类型,并发动攻击。
3.2 结构方程模型构建
根据实际的调研结果,卫星应用技术贡献度越大,卫星应用装备作战效能越强,则卫星应用能力越强,因此,卫星应用技术贡献度越大,卫星应用能力也越强。卫星应用技术体系、卫星应用装备体系、卫星应用能力体系是主要潜变量,分别构建它们的观测变量。结构方程模型中的显变量和潜变量如表2所示[12]。
根据结构方程模型理论和潜变量、显变量之间的关系,卫星应用体系评估结构方程模型如图4所示。
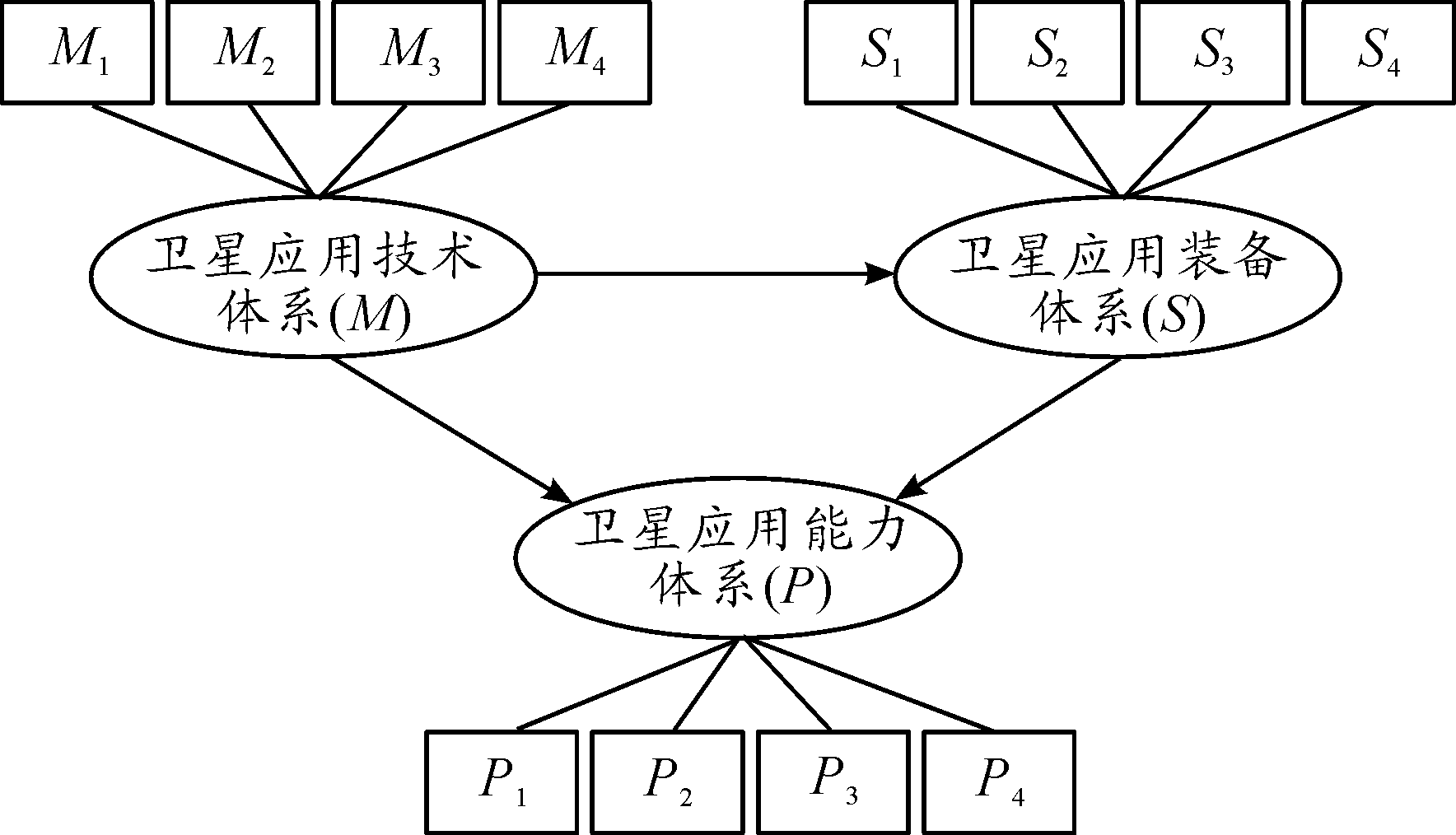
图4 卫星应用体系评估结构模型
表2 结构方程模型中的显变量和潜变量

其中,卫星应用技术体系是一个外生潜变量;卫星应用装备体系是一个内生中介变量,在受到卫星应用技术体系影响作用的同时,又作用于卫星应用能力体系;卫星应用能力体系是一个内生潜变量,同时受到卫星应用装备体系和卫星应用技术体系的作用。
依据卫星应用体系评估结构方程模型,建立卫星应用体系评估结构方程模型路径图,如图5所示。
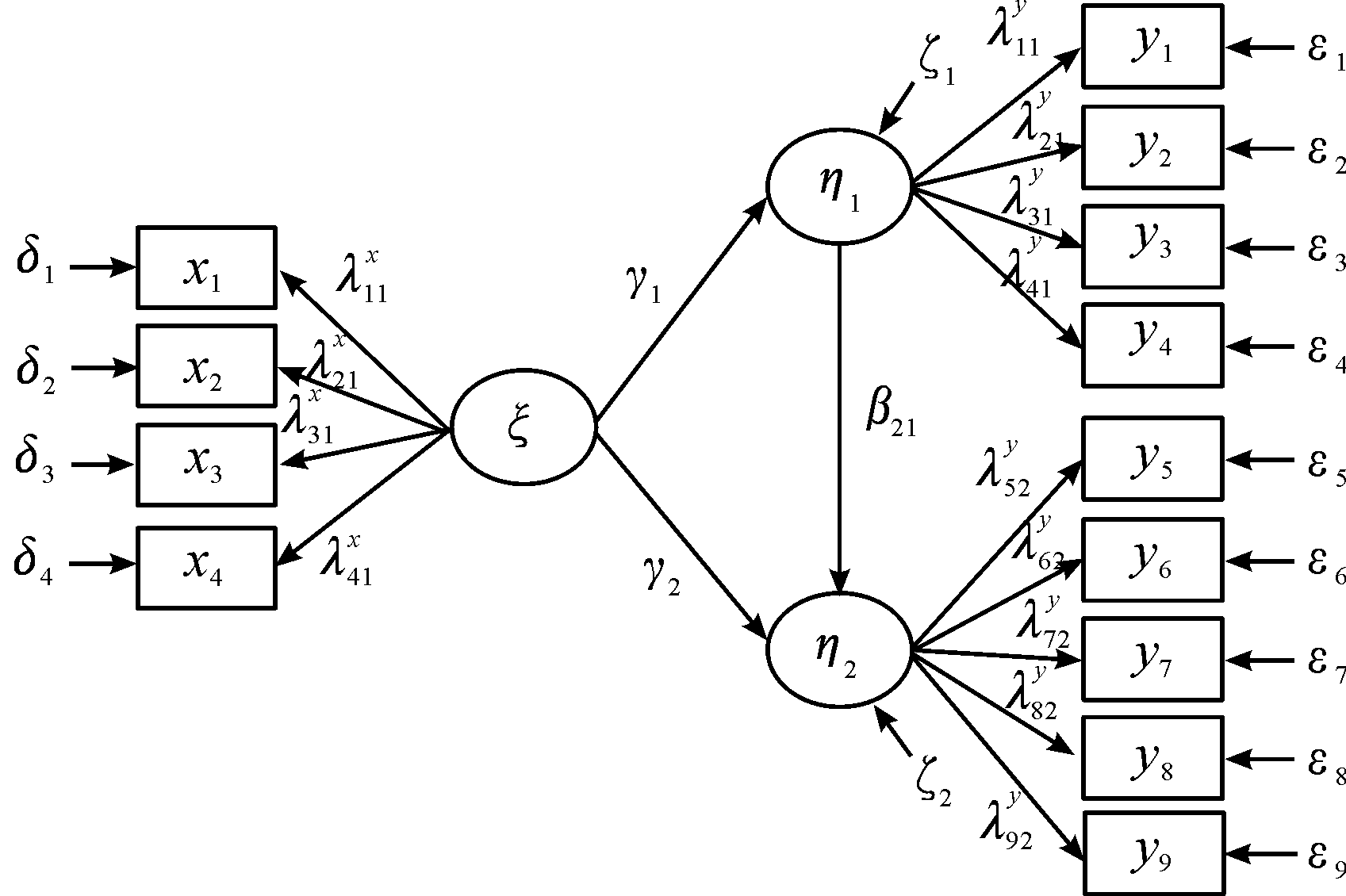
图5 卫星应用体系评估结构方程模型路径
结构方程模型可以表示为:
结构方程:
η=Bη+Γξ+ζ
即: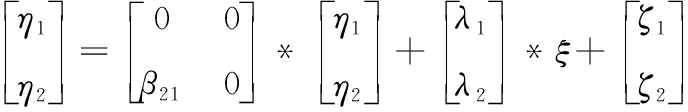
测量方程:
X=ΛXξ+δ
即: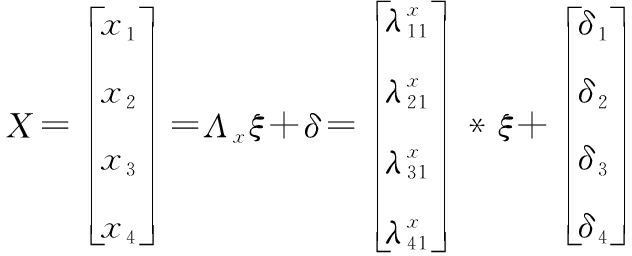
Y=ΛYη+ε
即:
模型中,外生显变量(用p表示)、内生显变量(用q表示)的数量分别为4个和9个,未知参数数量为31个,根据t规则,t=31≤(p+q)*(p+q+1)/2=91,所以结构方程模型是可以识别的。
根据结构方程模型测量方程推导,通过显变量来构建潜变量。
卫星应用技术体系评估模型:
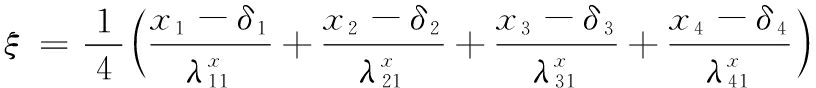
卫星应用装备体系评估模型:
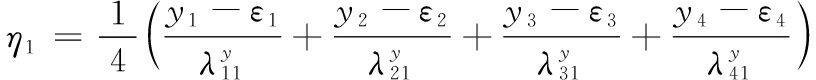
卫星应用能力体系评估模型:

根据结构方程模型结构方程推导,构建潜变量之间的线性关系。
卫星应用装备体系与卫星应用技术体系线性关系模型:
η1=λ1ξ+ζ1
卫星应用能力体系与卫星应用装备体系、卫星应用技术体系线性关系模型:
η2=β21η1+λ2ξ+ζ2
3.3 结果分析
由于缺乏真实的卫星应用体系样本数据,通过调查问卷的方法,收集获取500组卫星应用体系的样本数据。得到样本数据如表3所示,由于篇幅关系,此处只列举部分数据。
表3 卫星应用体系样本数据

使用AMOS构建模型,输入样本数据,进行参数估计,并对模型进行评估修正,最后得到结构方程模型的路径图,如图6。
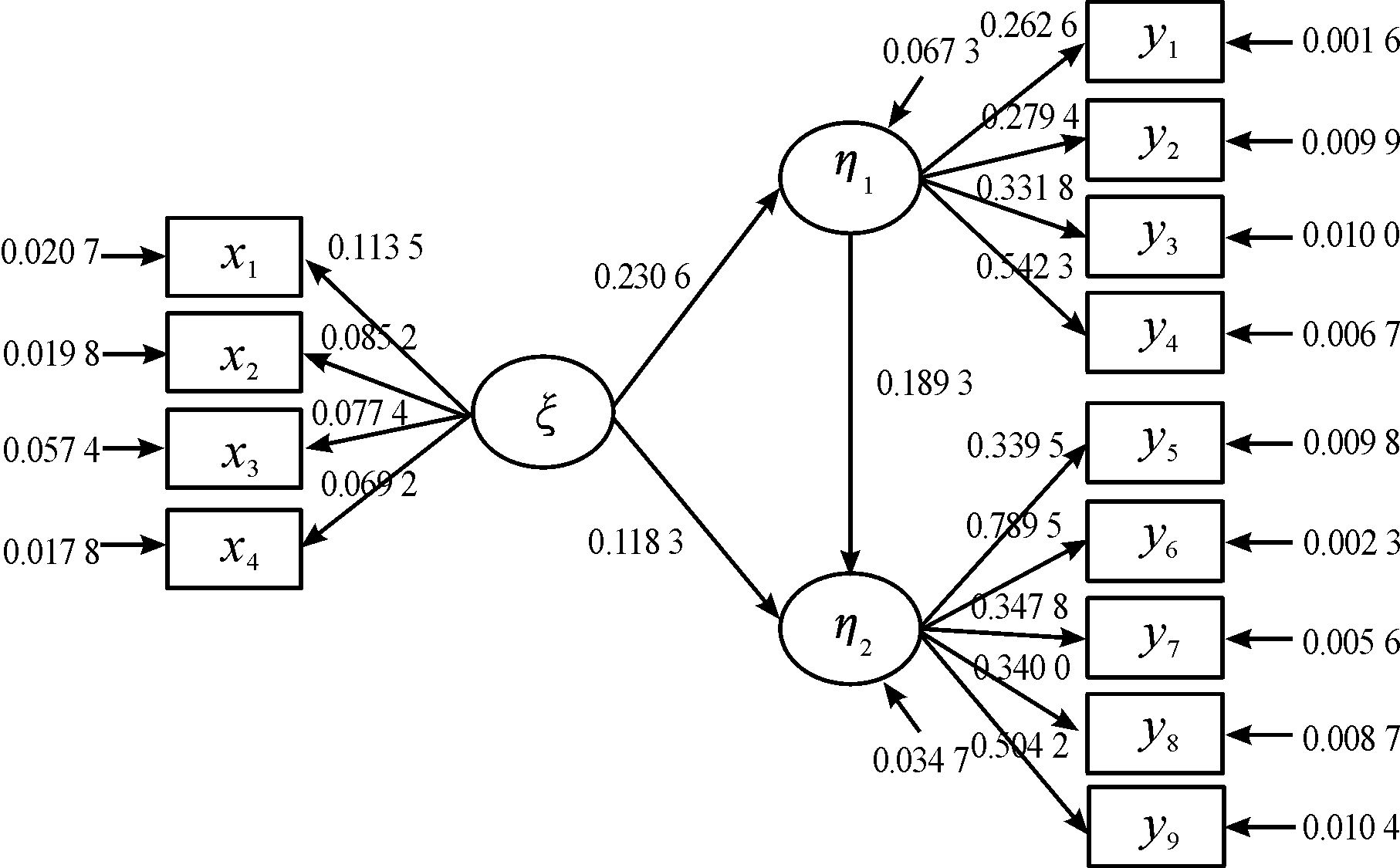
图6 结构方程模型路径
根据测量方程推导,通过显变量来构建潜变量。
卫星应用技术体系评估模型:
ξ=2.202 6x1+2.943 2x2+3.230 0x3+
3.612 7x4-0.176 8
卫星应用装备体系评估模型:
η1=0.952 0y1+0.894 8y2+0.753 5y3+
0.461 0y4-0.021 3
卫星应用能力体系评估模型:
η2=0.589 1y5+0.253 3y6+0.575 0y7+0.588 2y8+
0.396 7y9-0.018 7
从上述模型中潜变量与显变量之间的关系可以得出,相对于卫星应用技术体系,卫星应用终端技术、卫星信息处理技术、卫星系统运行控制技术、卫星应用体系构建技术的影响依次减弱;相对于卫星应用装备体系,信息获取类卫星应用装备、信息传输类卫星应用装备、时空基准类卫星应用装备、综合类类卫星应用装备的影响依次减弱;相对于卫星应用能力体系,太空侦察监视能力、太空导航定位能力、太空通信中继能力、战场环境监测能力、太空预警探测能力的影响依次减弱。
根据结构方程推导,构建潜变量之间的线性关系。
卫星应用装备体系与卫星应用技术体系线性关系模型:
η1=0.230 6ξ+0.067 3
卫星应用能力体系与卫星应用装备体系、卫星应用技术体系线性关系模型:
η2=0.189 3η1+0.118 3ξ+0.034 7
从上述模型中潜变量之间的关系可以得出,相对于卫星应用能力体系,卫星应用装备对提高卫星应用能力的影响更大;而相对于卫星应用装备体系,仅有卫星应用技术会影响卫星应用装备作战效能的发挥,与卫星应用能力无关,这也符合卫星应用体系的内在规律。
4 结论
结构方程模型在医学、统计学等民生领域得到广泛的应用,但在军事领域的应用尚不广泛。本文针对结构方程模型在卫星应用体系评估领域展开研究,对拓展太空信息在军事领域的应用具有重要意义。同时,本文也存在很多问题,如卫星应用体系评估指标不完善、模型的评估没有达到最优效果等,在下一步研究中将逐步改进。
[1] 李健宇.结构方程模型导论[M].合肥:安徽人民出版社,2004.
[2] 薛益新,马艳.装备作战能力和效能评估中有关问题的探讨[J].海军航空兵工程学院学报(军事科学版),2014(12):115-117.
[3] 林蒿.结构方程模型原理及AMOS应用[M].武汉:华中师范大学出版社,2008:1-6.
[4] 郝旭东,高进涛,刘道伟.基于结构方程模型的作战能力评估方法[J].火力指挥与控制,2014(12):115-117.
[5] 金璐.基于结构方程模型的我国财险公司偿付能力实证研究[D].大连:东北财经大学,2012:18-25.
[6] 侯杰泰,温忠麟.结构方程模型及其应用[M].北京:教育科学出版社,2006.
[7] 吴明隆.结构方程模型—AMOS的操作与应用[M].重庆:重庆大学出版社,2010:21.
[8] KEVIN J,GRIMM,NILAM RAM.Nonlinear Growth Models in Mplus and SAS[J].Structural Equation Modeling,2009(16):676-701.
[9] 林蒿.结构方程模型原理及AMOS应用[M].武汉:华中师范大学出版社,2008:1-2.
[10] 施令,杨凡德,强立.中段反导系统指挥控制能力评估指标体系研究[J].兵器装备工程学报,2018(2):106-110,118.
[11] 成浩,何新华,屈强,等.武器装备体系作战能力探索性评估方法研究[J].兵器装备工程学报,2018,39(5):1-4.
[12] 吴文刚,张志文,王庆生.基于模糊综合评判和AHP信息安全风险评估模型[J].重庆理工大学学报(自然科学),2017(7):156-161.
