作者简介:熊镐(1993—),男,硕士,主要从事弹道计算与气动仿真研究。
基于fluent的一级气体炮内弹道研究
Research on Internal Ballistics of Single-Stage Gas Gun Based on Fluent
气体炮是一种利用压缩气体做为动力源推动弹丸运动的发射装置,相比于以火药做为动力源的传统火炮,气体炮在获得较高初速的同时,不存在火炮发射时高温高压,发射相对稳定,安全可靠,且弹丸膛内运动时,需要承受的加速度和应力较小,炮身也不需要承受高温特性,使用寿命长。
现有主要的一级气体炮内弹道模型有两种,一种是基于等温膨胀假设的模型[1],一种是基于绝热膨胀假设的模型[2],后一种适用范围更广。这两种模型都是根据火炮内弹道模型演化而来,且都用平均膛压作为弹底压力计算弹丸运动情况,再采用次要功系数对模型进行修正。李锋等[3]在绝热膨胀模型的基础上,提出一种基于密度均匀假设的内弹道模型修正方案,考虑了气室容积对内弹道的影响,得到一种更准确的内弹道模型。这些模型都没有考虑阀门对膛内气流的影响。Z.J.Rohrbach等[4]提出一个根据通过阀门的气体流量计算气体炮内弹道的模型,并通过实验验证;文献[13]中也对阀控气体炮内弹道进行了研究,但这两种针对阀门流量的内弹道计算都是在有一定实验基础的前提下针对固定气体炮的内弹道计算。
为了研究气体炮内弹道过程中膛内气体流动状态,分析阀门对气体炮的影响,笔者利用计算流体力学商业软件fluent建立气体炮CFD模型,仿真分析了内弹道过程中气体炮膛内气体流动状态和弹丸的运动状态。
1 内道模型
气体炮工作时,气室内充满高压气体,当阀门打开,弹丸在高压气体的推力作用下沿着身管向前。图1所示为气体炮结构简化模型。
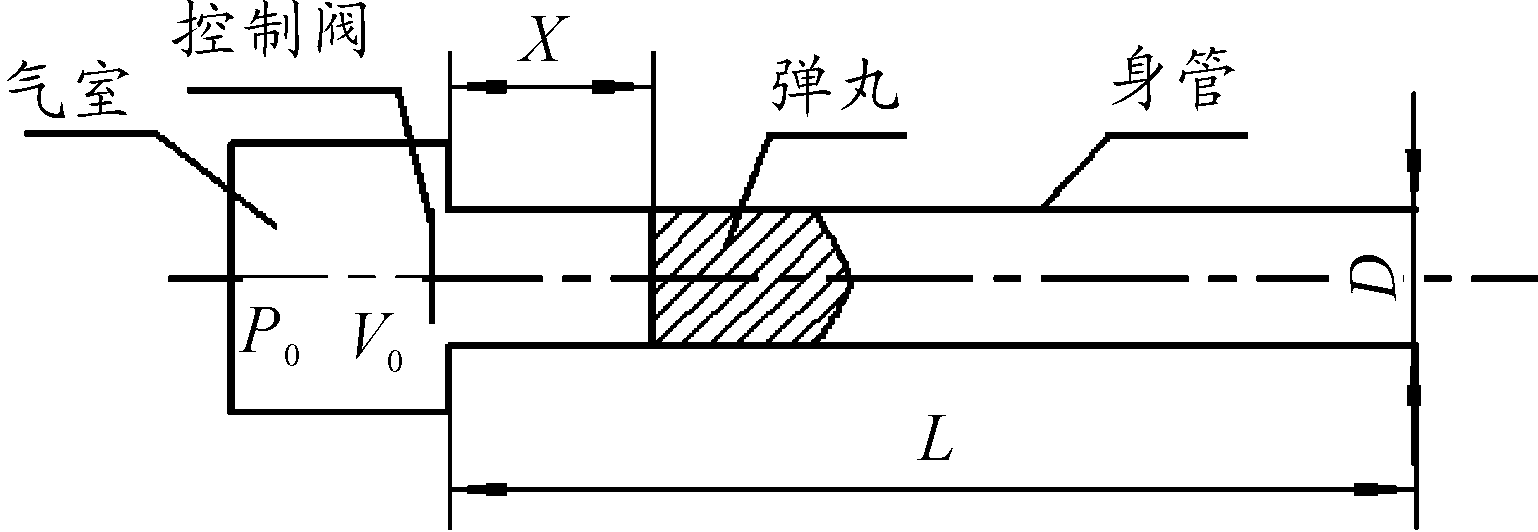
图1 一级气体炮基本结构简化模型
式(1)和式(2)分别为气体炮在绝热膨胀假设下和等温膨胀假设下的内弹道方程。假设气体为理想气体,通过气体动力学计算膛内平均压力,并引入虚拟质量系数φ,计算各类能量损失,最后根据牛顿运动定律积分得到[1,2,5]。
绝热膨胀假设下的内弹道方程:
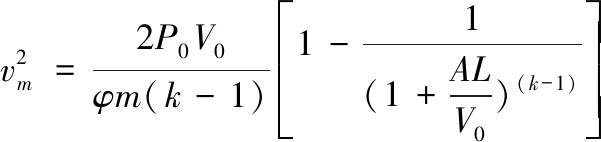
(1)
等温膨胀假设下的内弹道方程:
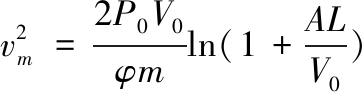
(2)
式(2)中:vm为弹丸初速;k为气体绝热指数;A为身管截面积;m为弹丸质量。
其中,次要功系数φ的表达式为
(3)
式(3)中:K为与摩擦力、弹丸旋转等能量有关的修正系数,本文中取1.05;式(3)等式右边第二项为气体动能修正,mg为气体质量,可通过气体状态方程方程得到。
2 CFD模型
2.1 控制方程
假设流体不可压缩,通过对连续性方程和动量守恒方程的求解来获得膛内流场的数值模拟。连续性方程和动量守恒方程[6]为
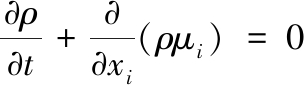
(4)
(5)
其中: p为静压; ρgi、Fi为重力体积力和其他体积力;τij为应力张量。
采用的湍流模型为RNG(重正化群) k-ε模型[7],湍动能k方程和湍能耗散率ε方程与标准k-ε方程相似,即:
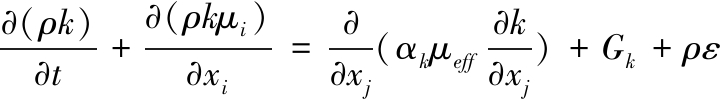
(6)
(7)
其中:
μeff=μ+μt
(8)
(9)
(10)
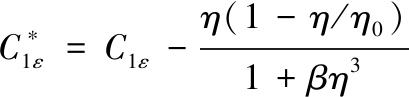
(11)
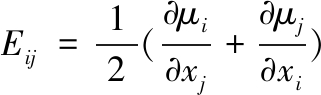
(12)
其中:Gk为平均速度梯度所引起的湍动能生成项;经验常数C1ε、C2ε、η0、β取值分别为1.42、1.68、4.377、0.012。
2.2 计算模型、网格划分及计算方法
本文选用空气做为气体工质,空气的相关参数:k=1.4,摩尔质量μmol=0.002 806 4 kg/mol。计算模型如图2所示,其中气室容积V0=1.8 L,身管长L1=1 m,阀门与弹底的距离L2=5 mm,口径D=35 mm,弹重m=0.3 kg,气室初始压力P0=10 MPa,初始温度为300 K。
为了达到提高计算效率的目的,本文将三维模型简化为二维模型计算。本文主要关注气体炮膛内气体流动状态,由于弹丸膛内运动速度较低,不会在弹前形成激波,相比于弹底压力,弹前空气阻力忽略不计。
动网格模型是用来模拟由于计算域边界运动而引起的计算域形状随时间改变问题的流体流动。动网格模型的关键技术是网格重新生成方法,本文同时采用弹簧光顺和局部网格重构两种方法,当变形较小时,采用弹簧光顺方法,当变形增大时,采用局部网格重构来避免网格质量下降[6]。网格模型如图3所示,网格数据为:网格数138 523个,节点数46 175个。
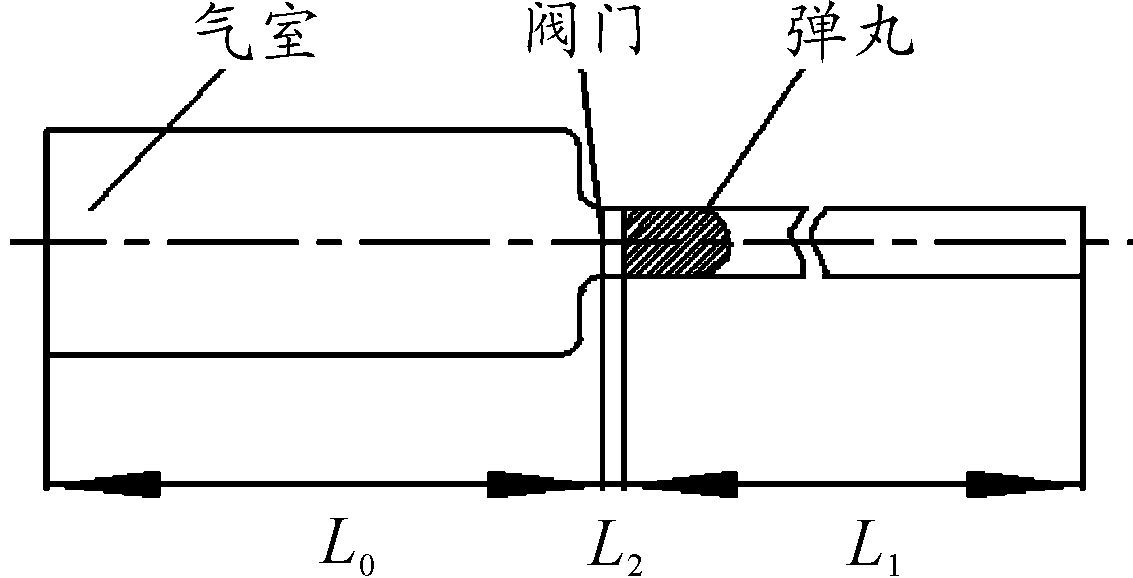
图2 气体炮计算模型
图3 弹体周围网格模型
由于阀门结构不同,且开启过程时间极短,这里忽略阀门开启过程,即假设阀门瞬间开启,在模型中不建阀门的模型,而是在fluent中利用patch功能定义阀门后的气室压力和阀门前的大气压力,实现阀门完全开启瞬间的压力条件。
在fluent中利用用户自定义函数(UDF)读取弹底压力变化和定义摩擦阻力,利用DEFINE_CG_MOTION函数赋予弹丸膛内运动。湍流模型选用上述的RNG(重正化群)k-ε模型,综合考虑计算的效率和精度,压力和速度耦合方法采用coupled算法,Green-Gauss Node Based压力方程利用PRESOT方法离散,动量方程,湍动能耗散率等均采用而二阶迎风方程(Second Order Upwind)来计算。
由于膛内气流流动状态变化迅速,从阀门打开到弹丸出膛口,总的时间约为10 ms,UDF通过读取弹体表面压力计算弹丸在时间步内的速度,一方面单位时间过长会造成本应该在时间步内降低的压力保持一定,导致计算结果不准确,另一方面,随着速度的增加,单位时间内运动的距离增大,会导致网格变形增大,不利于计算精度。本文根据多次计算分析,选1×10-7 s的时间步长。
3 计算结果与分析
图4和图5是有阀门和无阀门两种结构下的膛内气流速度云图和压力云图,图中所示为弹后空间内气体流动状态。
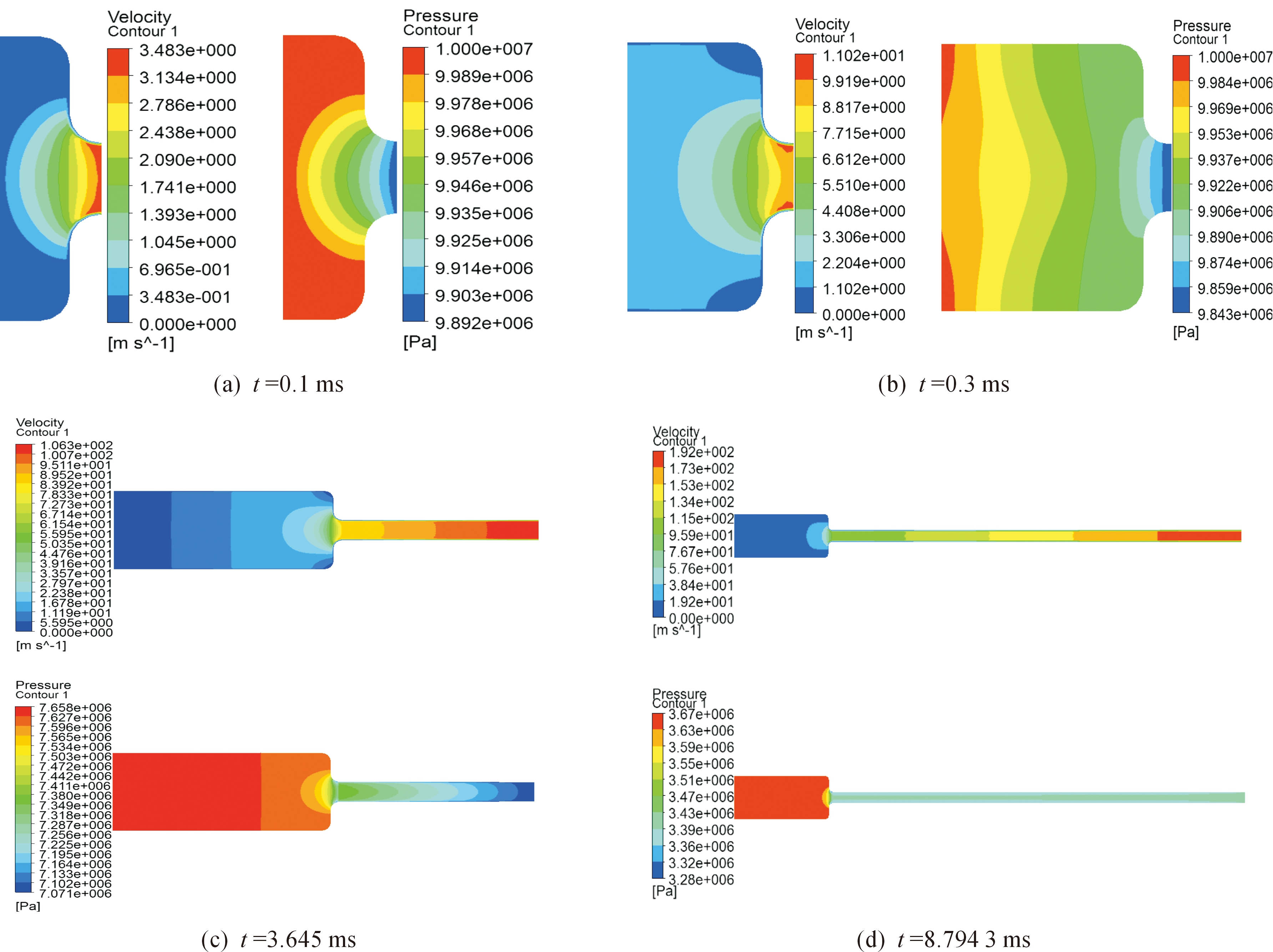
图4 无阀门时膛内气体流动状态
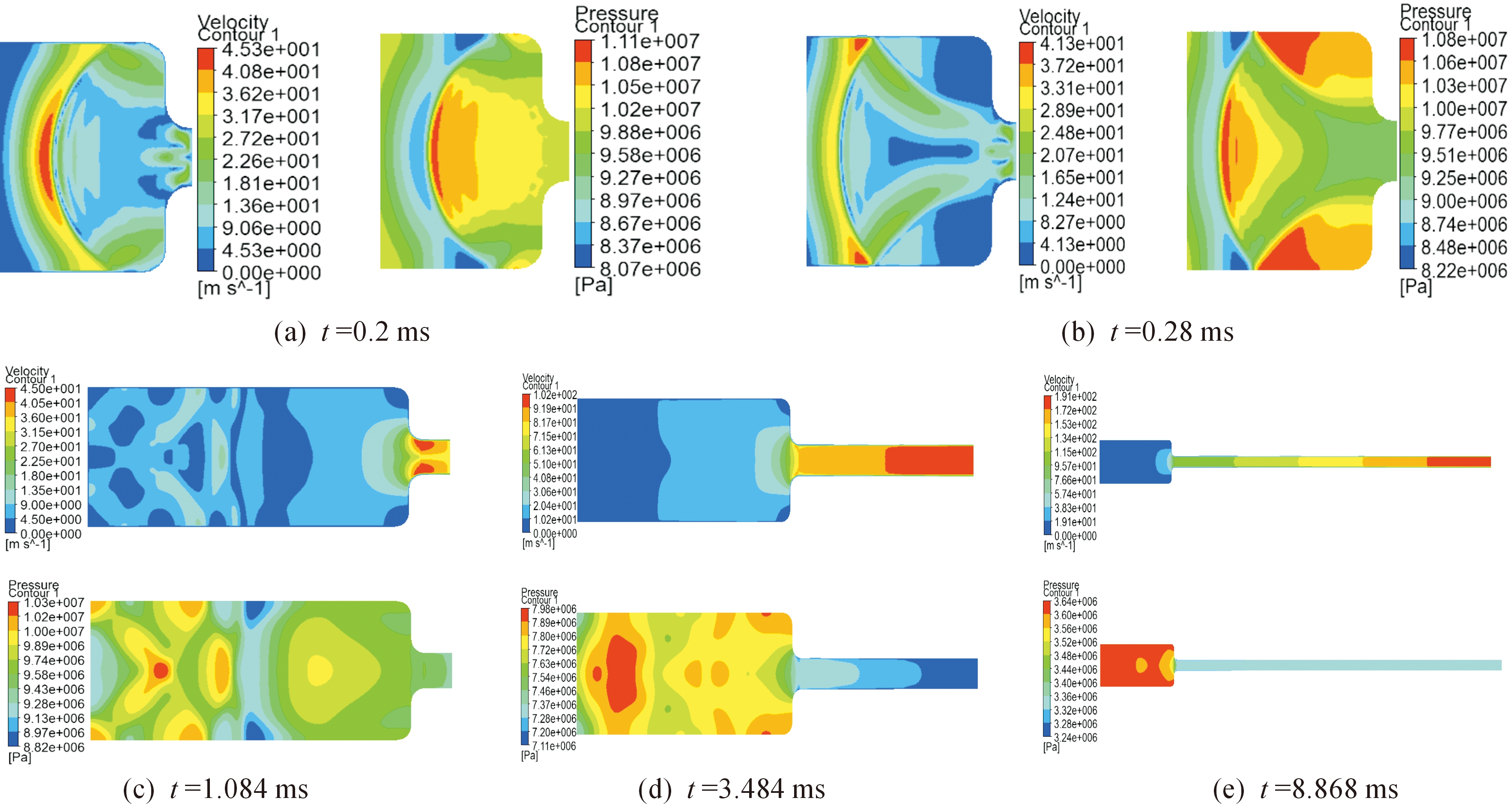
图5 有阀门时膛内气体流动状态
内弹道计算中,假设膛内气体速度线性线性分布[8],即:
(13)
式中:u为膛内内任意位置的速度。
由图4速度云图可以看出,无阀门时,弹后空间中,身管内的气体基本保持线性分布,但是在气室与身管连接处存在较大的速度梯度,这是由于身管与气室连接处存在较大的收缩比,由气体动力学理论可知,亚声速气流在截面积逐渐缩小的管道内将不断加速[9],传统火炮内弹道计算假设膛内气体速度线性分布,一方面火炮膛压高,气流速度较快;另一方面,火炮弹膛与身管截面积变化较小,截面积变化对膛内气流的影响较小。对于同一种气体工质,在相同温度下,气体做工能力主要和压力和气室容积相关[10],因此,气体炮往往有极大的气室容积和收缩比,气体炮内弹道计算不能只考虑膛内气流线性分布,还应充分考虑收缩比变化对气体流动状态的影响。
图5所示为有阀门时膛内气体流动状态,可以看出,阀门打开后,气体先是向前流动(身管指向为前),当气流流到弹底时,弹丸开始运动,由于气流速度远高于弹丸速度,气体开始回流,当回流与来流相遇,形成弹后气体复杂流动状态,经过极短时间后,弹后气体形成向气室底部传递的激波,一方面,来流与回流相遇形成气室中心的激波,激波前后有压差和速度差造成了图5中的压力云图与速度云图的局部断面,另一方面,激波在气室壁面上的反射使壁面附近形成高压区域,激波在膛内的反复传递形成了膛内压力和气流速度的不均匀。
图6所示为弹后压力的变化曲线,可以看出,有阀门结构时,弹底压力在阀门打开时,先是迅速的上升,达到了最大约12.2 MPa的弹底压力,之后在11 MPa上下剧烈的变化,直到约0.2 ms,弹底压力开始下降,然后保持一定的规律在无阀门结构弹底压力曲线上下波动,直到约3.5 ms,随着弹丸速度和位移的增加,弹丸逐渐远离气室,气室内气流的波动对管内气流的影响逐渐减小,弹底压力逐渐趋于稳定,并且与无阀门结构的弹底压力一致。由图6、图7可以看出:无阀门结构与有阀门结构在内弹道初期,弹底压力有较大的不同,但是整个内弹道过程中,有阀门结构的压力曲线主要在无阀门结构弹底压力曲线上下波动,最终保持一致,弹丸运动速度始终保持较高的一致性。
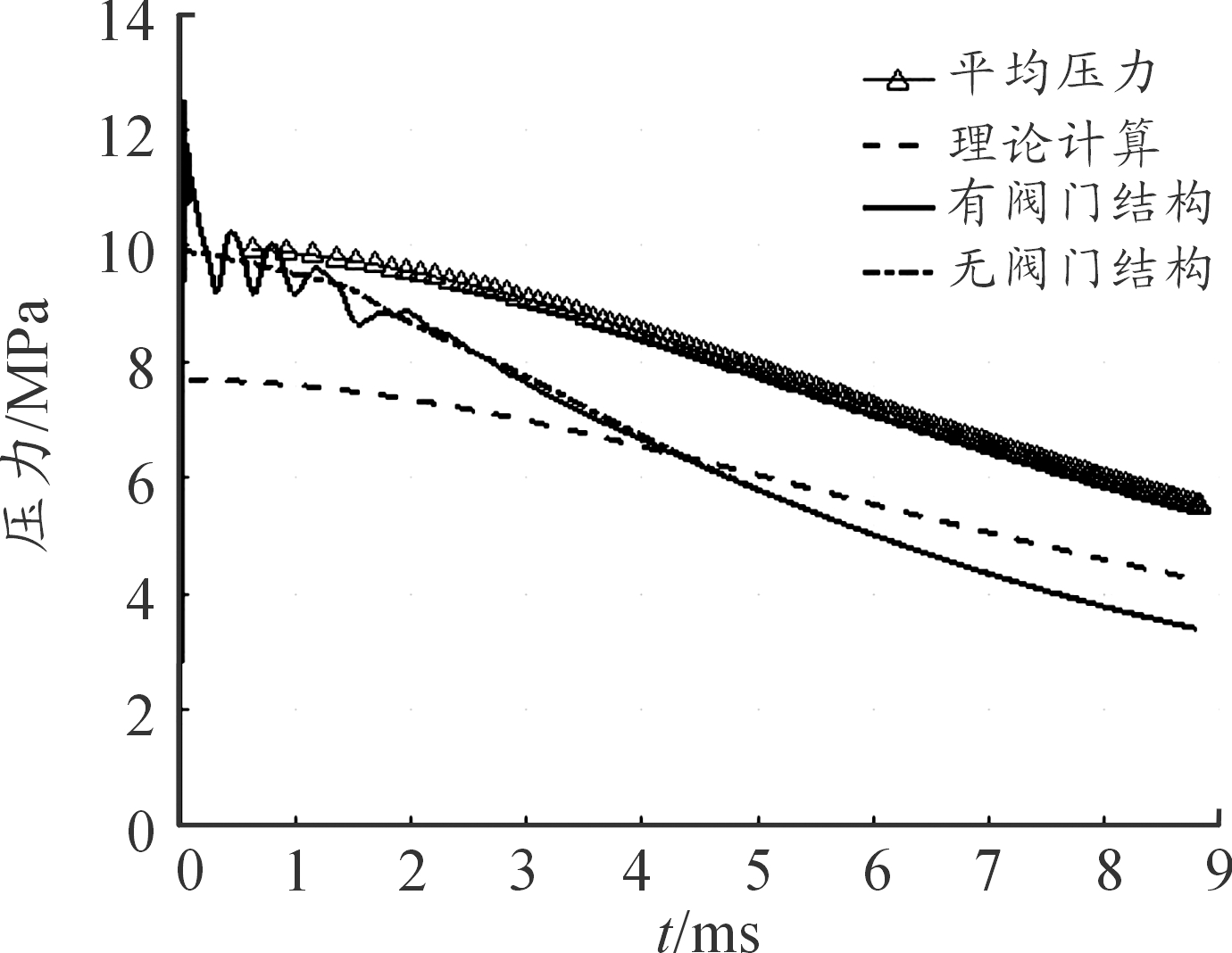
图6 弹底P-t曲线
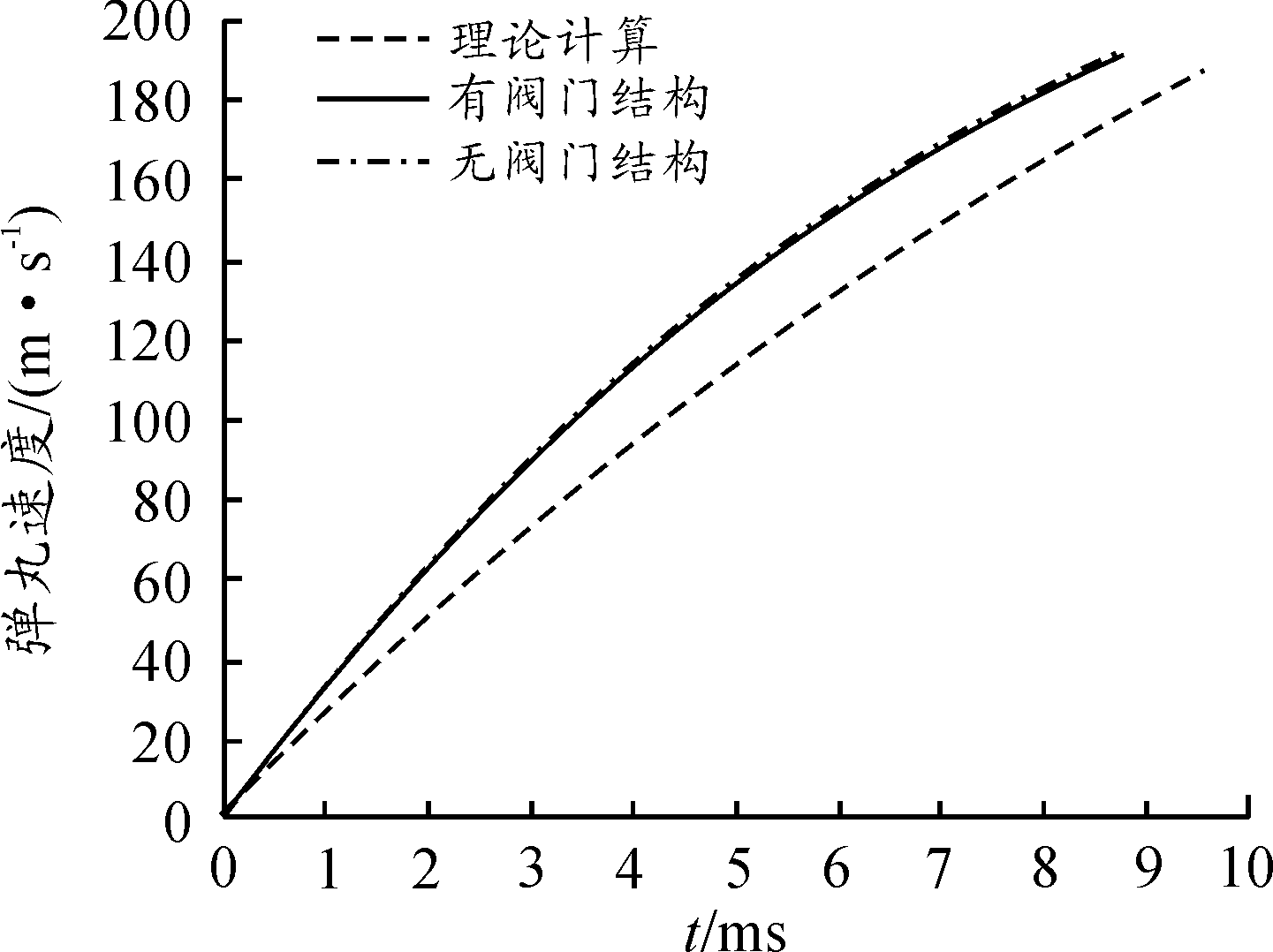
图7 弹丸v-t曲线
图6、图7、图8中理论内弹道模型与仿真结果可以看出:膛内平均压力与仿真结果的弹底压力有较大的区别,内弹道计算中用次要功系数与平均压力计算弹丸运动情况,计算出的弹底压力与仿真结果仍有较大的误差,且弹丸速度也远低于仿真结果。
表1所示为弹丸初速的对比结果可以看出:与实验数据相比,fluent仿真结果与理论计算模型有相同的弹丸速度变化规律,且仿真结果与实验结果的误差很小,相比于理论计算的结果更接近实验结果。由图4可以看出,气流在身管与气室连接处有较大的速度和压力梯度,式(3)中气体动能项未考虑气室容积和收缩比造成的膛内气流状态变化,从而造成弹底压力计算不准确。
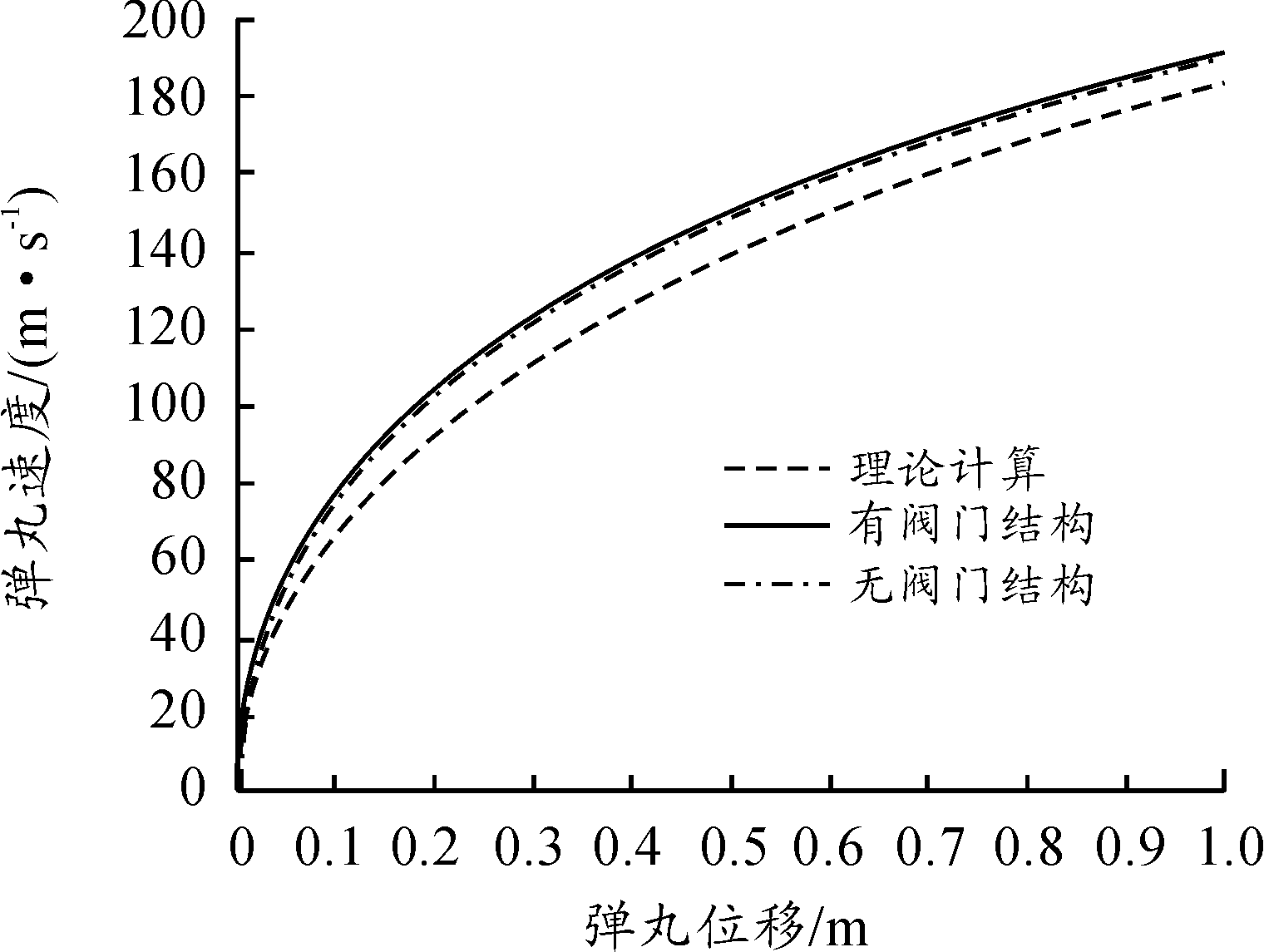
图8 弹丸v-L曲线
表1 弹丸初速对比

4 结论
本文利用fluent动网格技术和UDF对气体炮内弹道过程进行了仿真,有阀门结构会造成弹底气体回流,内弹道初期弹底压力反复变化,但是随着弹丸速度和位移增加,气室内气流运动对弹丸影响减小,弹底压力逐渐与无阀门结构的弹底压力一致,两种结构的弹丸速度变化情况基本一致。但阀门会影响膛内气流状态,当身管长度较小时,应尽量减小弹底与阀门的距离,减小气流加速距离,减小对气体流动状态的影响。
对比仿真结果和现有内弹道计算模型,认为现有计算模型在弹底压力计算上未考虑气室容积和收缩比对膛内气流的影响,导致弹丸运动速度计算结果低于实际结果,fluent仿真的结果相比于理论模型更接近实验结果,在气体炮内弹道的研究上具有一定的可信度。
[1] DENNY M.Internal ballistics of an gas gun[J].Phys.Teach,2011,49:81-83.
[2] 赵俊利,高跃飞.气体炮实用内弹道技术研究[J].太原理工大学学报,2003(3):288-290.
[3] 李锋,拜云山,冯晓伟.一级气体炮内弹道方程修正及验证[J].弹道学报,2016,28(1):14-18.
[4] ROHRBACH Z J,BURESH T R,MADSEN M J.Modeling the exit velocity of a compressed gas gun[J],Am.J.Phys.,2012,80(1).
[5] 丁廷哲.有限容积高压气源高效膨胀技术研究[D].南京:南京理工大学,2017.
[6] 温正.fluent流体计算应用教程[M].北京:清华大学出版社,2013.
[7] 张师帅.CFD技术原理与应用[M].武汉:华中科技大学出版社,2016.
[8] 张小兵.枪炮内弹道学[M].北京:北京理工大学出版社,2014.
[9] 王新月.气体动力学基础[M].西安:西北工业大学出版社,2006.
[10] 王焕然.一种新型压缩空气储能系统理论分析[J].南方能源建设,2015(2):16-19,56.
[11] 刘海刚.杀伤元气动模拟发射技术研究[D].太原:中北大学,2017.
[12] 赵俊利,曹锋.气体炮实用内弹道方程及应用[J].火炮发射与控制学报,2003(3):48-51.
[13] 庞博,尚彬彬,张佳俊,等.阀控气体炮内弹道建模及实验研究[J].兵器装备工程学报,2018(9):51-53.
