作者简介:韩伟(1982—),男,博士研究生,高级工程师,主要从事高效毁伤技术研究。
锆钽复合药型罩EFP成型及侵彻研究
Investigation of EFP Forming and Penetration of Ta/Zr Double-Layered Shaped Charge Liner
第二次世界大战以来,随着制导精度的提高和破甲能力的增强,聚能战斗部已经在反装甲武器上得到了广泛应用[1]。但随着复合、复反应装甲和贫铀装甲等技术的出现,各种军事目标的防护能力不断加强,使得传统聚能战斗部迎来了巨大的挑战。为实现对目标的高效毁伤,近年来人们提出双层药型罩、含能药型罩等各种弹药设计来提高聚能装药对新型装甲的侵彻能力。传统的聚能装药都是单层罩结构,利用其形成的射流或EFP(爆炸成型弹丸)进行动能侵彻和毁伤。而根据材料阻抗匹配关系,设计双层含能药型罩可以获得更高的压垮速度,能量转换与吸收机制更有效,侵彻性能更强。
Phillips通过对金属材料的物理属性和经济性等方面的考量,认为目前可适用于制造药型罩的金属有紫铜、铝、钽和锆等[1]; Faibish[2]制备了双层焊接药型罩,对小锥角双层药型罩射流成型过程进行了数值仿真和实验研究;臧涛成等[3]发现了双层药型罩相比于单层药型罩的优势,形成的射流侵彻能力更强;Weiman K和Blache A为了提高EFP的侵彻能力和飞行稳定性,提出了外铁内钽的双层药型罩形成EFP的技术方案[4]。
综上所述,国内外陆续开展了多层药型罩的研究,以求增强聚能装药的毁伤效果。利用活性材料代替外层惰性金属,由其形成的EFP尾部材料随进EFP头部的开孔,发生化学反应,释放化学能,扩大毁伤效果[5,6]。本文提出外层为锆,内层为钽的双层含能药型罩设计。内层钽形成EFP头部侵彻靶板,外层锆随进在靶后放热产生后效。由于很难对EFP成型和侵彻进行理论研究,且为了减少实验的成本,本文采用AUTODYN软件模拟EFP成型,研究典型大锥角装药结构下不同厚度的锆/钽双层药型罩形成EFP速度及对靶板侵彻规律,得到典型大锥角双层含能药型罩不同内外罩厚度比的成型情况,并进行了部分实验验证,对于锆/钽双层含能药型罩的研究具有重要的指导意义。
1 理论模型分析
1.1 EFP的成型分析
多年来,学者们进行了大量仿真和实验研究,但对于EFP成型的理论分析没有太多进展。得出的EFP的成型过程大致为:EFP的成型伴随着压垮和翻转。压垮就是炸药起爆后,药型罩受到爆轰波的压缩发生压垮现象,压垮的程度与炸药的材料、起爆方式、起爆点的选择和药型罩的材料及加工方式等众多因素有关。而EFP发生翻转是因为部分微元的速度无法克服材料的屈服强度,无法运动到轴线上。按照郑宇[7]的理论,将大锥角的药型罩分为如图1所示的3个区域。
1.2 双层药型罩EFP压垮计算
由PER理论[8]得出射流速度方程:

(1)
其中,V0为压垮速度,α为药型罩半锥角,δ为药型罩微元的极限偏转角,β为压垮角。
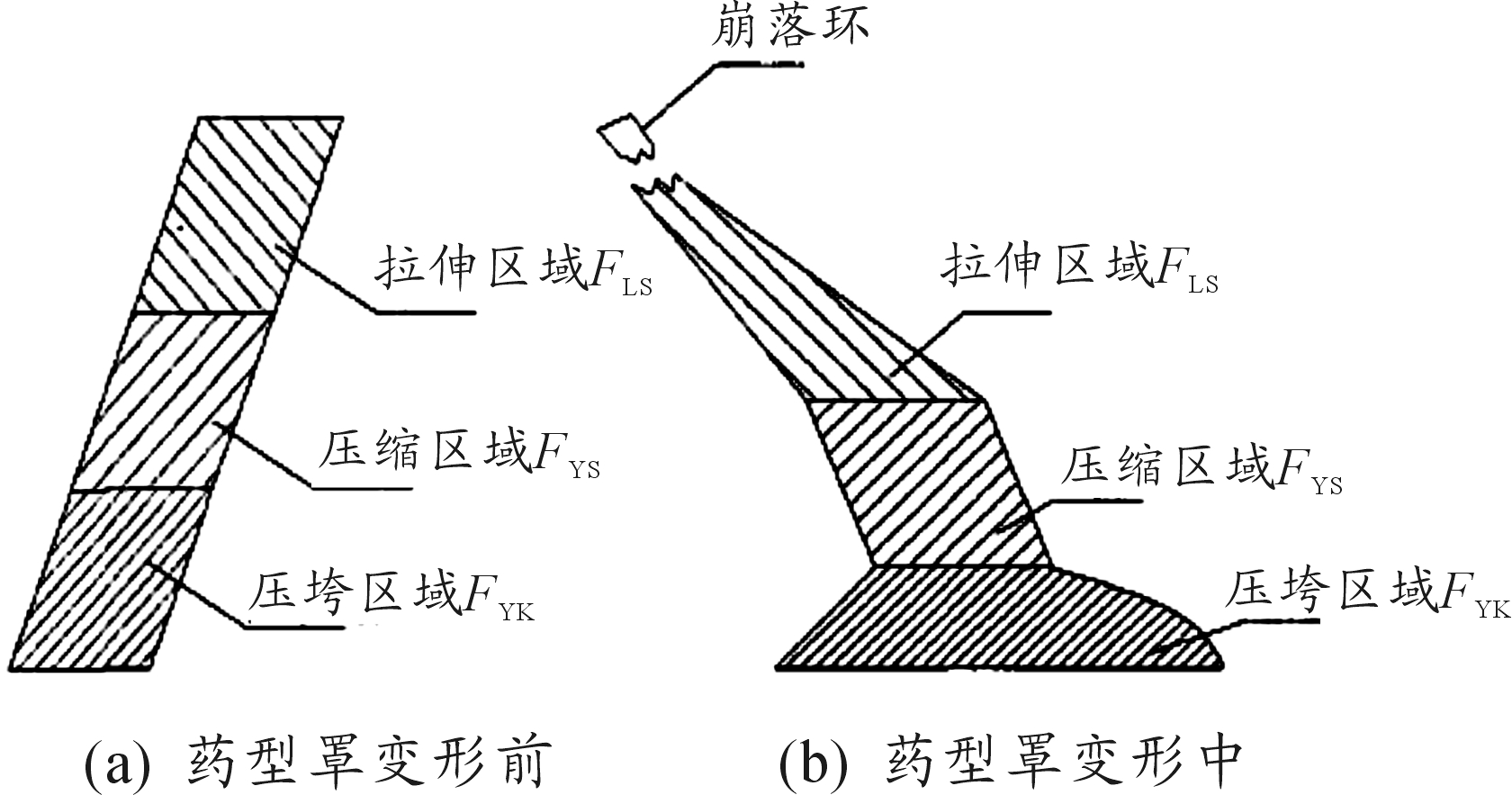
图1 大锥角药型罩的变形[7]
药型罩微元压垮速度简化公式[9]:

(2)
其中,B为考虑装药、药型罩结构、爆轰波入射角等多种影响因素的系数,b为双层药型罩壁厚,ρ为双层药型罩微元平均密度,P为内层铜罩压垮压力。
炸药爆轰后,冲击波运动至药型罩表面时会发生透射和反射现象,透射波和反射波的性质由相邻介质材料本身决定。爆轰冲击波从低阻抗(R0)炸药传到高阻抗(R2)紫铜界面上时,反射波压力为Pr2,透射波压力为Pt2,阻抗失配方程的基本形式为:

(3)
式中,P0为炸药爆轰初始压力。
基于复合材料系统中的阻抗适配原理[9-10],当在炸药和紫铜罩中间加入阻抗为R1(R0<R1<R2)的材料后,作用在紫铜上的透射压力将增大为:
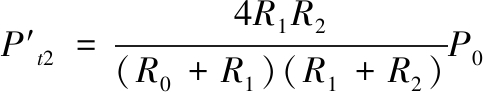
(4)
可以看出,通过配置合适的外层罩材料可以提高双层药型罩微元压垮速度,增大射流速度。
2 数值模拟
聚能装药EFP的形成和侵彻是一个高压、大应变的过程。非线性动力学仿真软件AUTODYN可以很好的解决大变形过程。本文使用AUTODYN软件模拟EFP的成型与侵彻问题。Euler算法适宜求解大变形和流体流动问题,但是耗费大量的求解资源。本文在计算EFP的形成时,选用Euler算法,而EFP侵彻靶板宜采用Lagrange算法。在仿真过程中,当应力波或爆轰产物到达边界时会发生应力波固壁反射以及爆轰产物回流,将对仿真结果产生很大影响,故设置边界条件为“Flow-out(All Equal)”,假设所有的物质可以无障碍流出,且应力波可以在边界无反射传播出去。由于聚能装药结构为对称圆柱体,在仿真中为减少求解时间,将其简化为二维轴对称模型。
2.1 计算模型
仿真计算聚能装药采用60基准弹无壳体装药结构,以140°锥形药型罩为原型,主装药为8701炸药,中心点起爆,装药结构示意图为图2,结构参数值见表1。
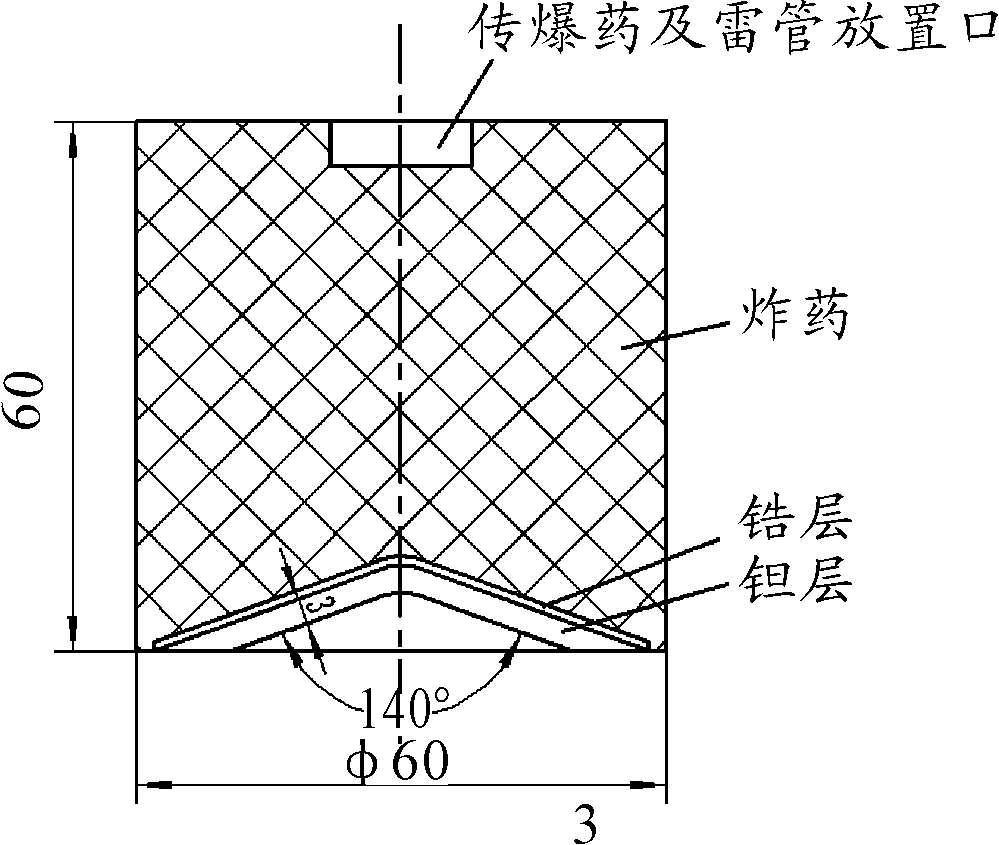
图2 聚能装药结构示意图
表1 聚能装药药柱参数值
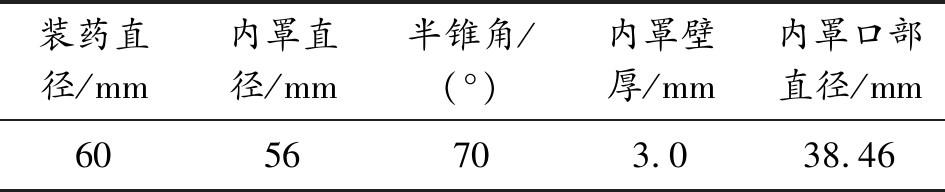
药型罩选用内外罩壁厚比为1/3、2/3、3/3三种结构进行计算。图3为双层药型罩内外罩厚度比为3/3的有限元模型,模型由空气域、主装药、壳体、外罩和内罩构成。由于EFP的形成和侵蚀过程都是在轴线位置上发生的,因此为计算的方便,轴线附近的网格设置为0.2×0.2,其他网格为0.5×0.5。
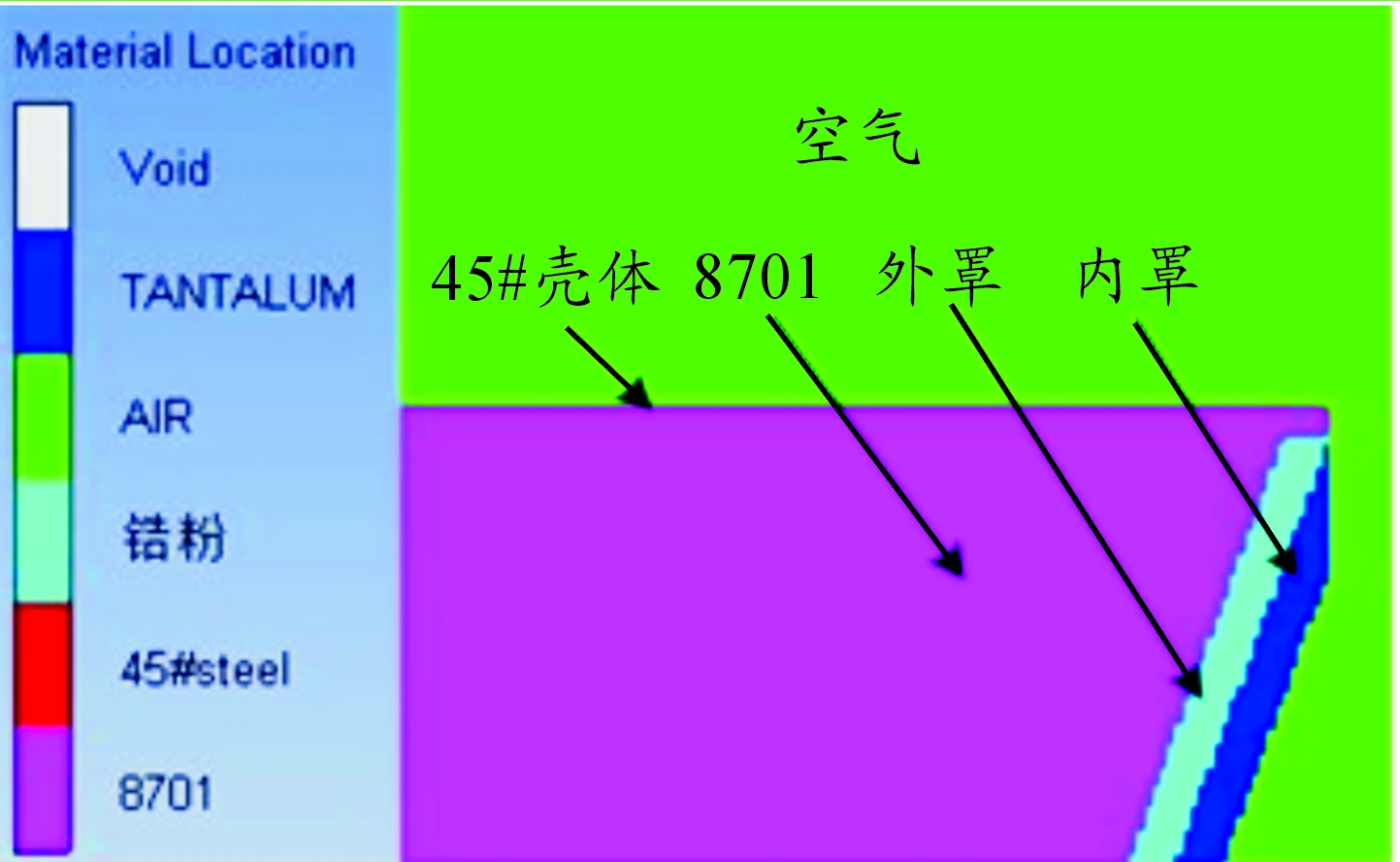
图3 锆/钽药型罩内外厚度3/3的二维计算模型
2.2 材料模型
选取锆和钽两种金属作为双层药型罩材料。锆的密度比钽小得多,但材料声速比钽略大,声阻抗介于炸药和钽之间,根据上一节理论分析可知,这样的结构有利于增大药型罩压垮速度。材料状态方程和强度模型如表2所示,其物理参数如表3所示。表中C为材料声速;γ0为Gruneisen系数。
主装药选用8701炸药,计算采用高能炸药燃烧材料模型和JWL状态方程共同描述炸药爆轰过程。JWL状态方程表达式为[6]
pu=Fpe(V,E)
(8)
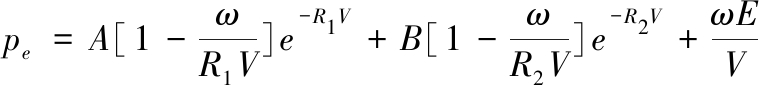
(9)
式中: pu为任意时刻炸药微元所释放的压力;pe为来自JWL状态方程的炸药爆轰产物压力; F为炸药燃烧质量分数; V为相对体积;E为单位体积内的内能密度;e为比动能。
表2 各材料状态方程及强度模型

表3 药型罩材料物理参数

8701炸药的JLW方程中的主要参数如表4所示,其C-J参数如表5所示。表中ρ为实验制备主装药的平均密度;D为爆速;e0为初始比动能。
表4 8701炸药JWL状态方程参数
表5 8701炸药C-J参数

2.3 高斯点设置
设置动、静态高斯点跟踪和监测材料相关信息:动态高斯点附着在罩材料上,可以实时显示罩材料流动的位置,记录药型罩压垮过程中对应材料的速度、密度、应力等的动态数据。计算结束后判读各个高斯点的速度、位置等信息,比较内外罩不同厚度比情况下EFP的速度状态及成型情况。
如图4所示,在轴线上的药型罩两端,共设置三个流动高斯点,以其瞬时监测EFP从形成到侵彻等一系列过程的速度、密度、压力等参数,还在Euler区域的轴线上每隔50 mm设置一个固定高斯点,以其监测冲击波和EFP经过时速度、密度等信息的变化。
设置高斯点记录EFP成型过程中的数据信息,计算结束后对数据进行处理便可分析出任意时刻EFP成型性能及材料流动情况。

图4 计算模型局部高斯点设置
3 仿真及实验结果分析
3.1 锆钽双层药型罩EFP成型结果
以内外罩厚度比3∶3为例,如图5所示,炸药爆轰后约0.02 ms时药型罩被压垮,内外罩同时发生变形,内罩形成EFP头部。运动至0.13 ms时双层罩同时翻转,外罩向后流动形成尾部。在大约0.86 ms时EFP基本完成最终成型。

图5 锆钽双层药型罩EFP成型过程
对1/3、2/3、3/3壁厚下锆/钽双层药型罩结构进行EFP成型数值计算,EFP飞行至约500 mm(9倍炸高)时各装药结构EFP成型基本完成,此时的EFP速度最大,如图6所示。从锆/钽药型罩形成的EFP图6(a)、(b)、(c)分析对比可以看出,在相同的装药及起爆条件下,随着含能层(锆层)厚度的增加,EFP的翻转形成弹丸长径比变小,这将导致其飞行速度衰减快,侵彻能力下降。
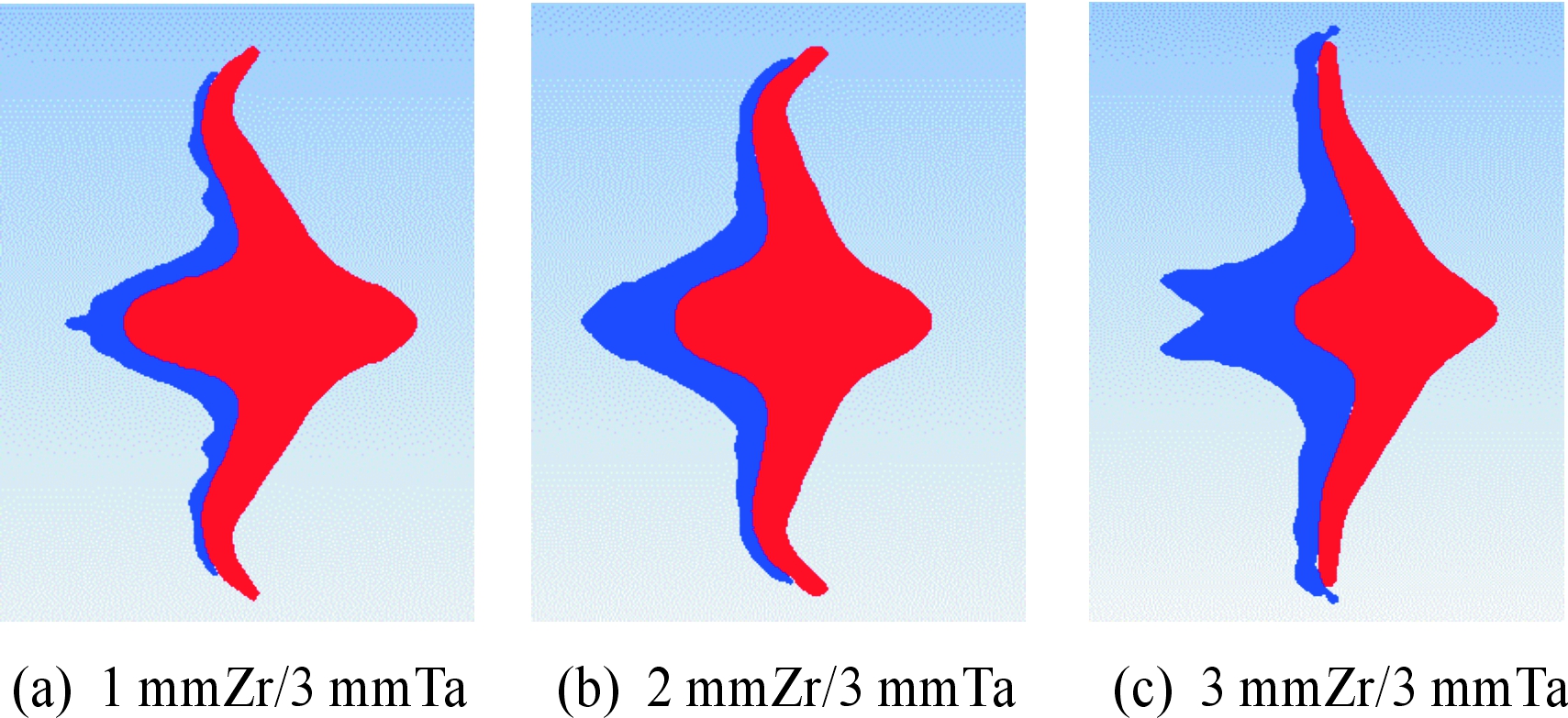
图6 双层药型罩EFP成型结果
3.2 双层药型罩EFP侵彻靶板
对1/3、2/3、3/3壁厚下锆/钽双层药型罩结构进行EFP后对半无限45#钢靶板的侵彻进行数值仿真,在9倍炸高下的侵彻速度最高,侵彻能力最好,对比3种不同内外罩厚度比药型罩形成EFP侵彻45#钢侵彻结果如图7所示。显然,在同一装药结构条件下,相同位置处,随着外罩厚度的增加,EFP的侵彻深度下降。

图7 在9倍装药口径炸高处EFP侵彻情况
将1 mmZr/3 mmTa双层药型罩、2 mmZr/3 mmTa双层药型罩、3 mmZr/3 mmTa双层药型罩形成EFP对半无限靶侵彻的3种仿真结果加以对比分析,见表6,表7和表8。
表6 1 mmZr/3 mmTa药型罩EFP侵彻仿真结果

表7 2 mmZr/3 mmTa药型罩EFP侵彻仿真结果
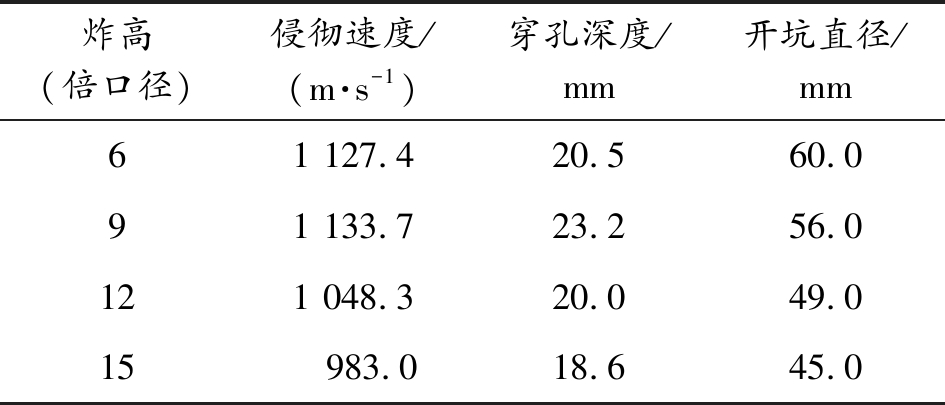
表8 3 mmZr/3 mmTa药型罩EFP侵彻仿真结果

相同药型罩厚度下,在6~9倍口径炸高左右,EFP的速度最大和侵彻能力最强;当炸高继续增大的情况下,EFP的速度和侵彻能力受到的影响越来越小。
锆/钽双层药型罩在内层钽厚度不变的情况下,随着外层锆厚度增加,EFP成型后的速度和穿透靶板的能力都有所下降,但开坑直径差距不大。
3.3 双层药型罩侵彻靶板实验结果
采用粉末冶金方法制备的双层药型罩,选取仿真结果较好的1 mmZr/3 mmTa双层药型罩与60 mm铜基准罩,于9倍装药口径炸高下进行侵彻45#钢靶(35 mm)+2A12Al(2 mm)实验,其侵彻及后效毁伤结果为图8、图9。

图8 1 mmZr/3 mmTa双层药型罩侵彻45#钢实验结果

图9 60 mm铜基准罩侵彻45#钢实验结果
由图8所示为1 mmZr/3 mmTa双层药型罩侵彻结果,钢靶正面有明显的材料破碎后侵彻痕迹,表明EFP的成型后部分破碎;对钢靶侵彻深度约为32 mm,开坑直径约为50 mm,与仿真结果吻合较好;钢靶靶后崩落使整个侵彻孔贯通,EFP材料穿过45#钢靶,在崩落物和部分破碎的EFP共同作用下,对后效铝靶产生扩孔,铝靶表面有明显的熏黑,表明药型罩侵彻后的释能效果明显。
图9为60基准罩的侵彻结果,对钢靶侵彻开坑直径约为50 mm,侵彻深度34 mm。同样,对后效铝靶有开孔,铝靶表面有黄色痕迹,未见明显的反应效果。
研究后效铝靶表面残留物元素成分,分析药型罩的释能行为,对表面残留物进行能谱仪(EDS)元素分析,图10所示。图10为锆钽双层药型罩侵彻后铝靶表面残留物EDS分析图,其结果表明:在铝靶上残留物元素主要为锆、钽、铁和氧,氧含量很高,表明侵彻后发生了氧化反应,验证了锆钽双层药型罩释能特性。图11为60 mm铜基准罩侵彻后铝靶表面残留物EDS分析图,其中主要有铜、铁、铝三种元素,氧元素含量很低,表明几乎未发生氧化反应,无释能特性。
1 mmZr/3 mmTa双层药型罩和60 mm铜基准罩在侵彻能力上差距不大,但是1 mmZr/3 mmTa双层药型罩具备靶后释能特性,具有更强的后效毁伤效果。
高效毁伤聚能战斗部外层罩为锆,内层罩为钽的双层含能药型罩,可实现延展性优秀的内层钽形成EFP头部侵彻靶板,外层锆随进发生反应并在靶后迅速放热产生后效,对靶后目标(干草、棉絮、煤油等)进行有效引燃。
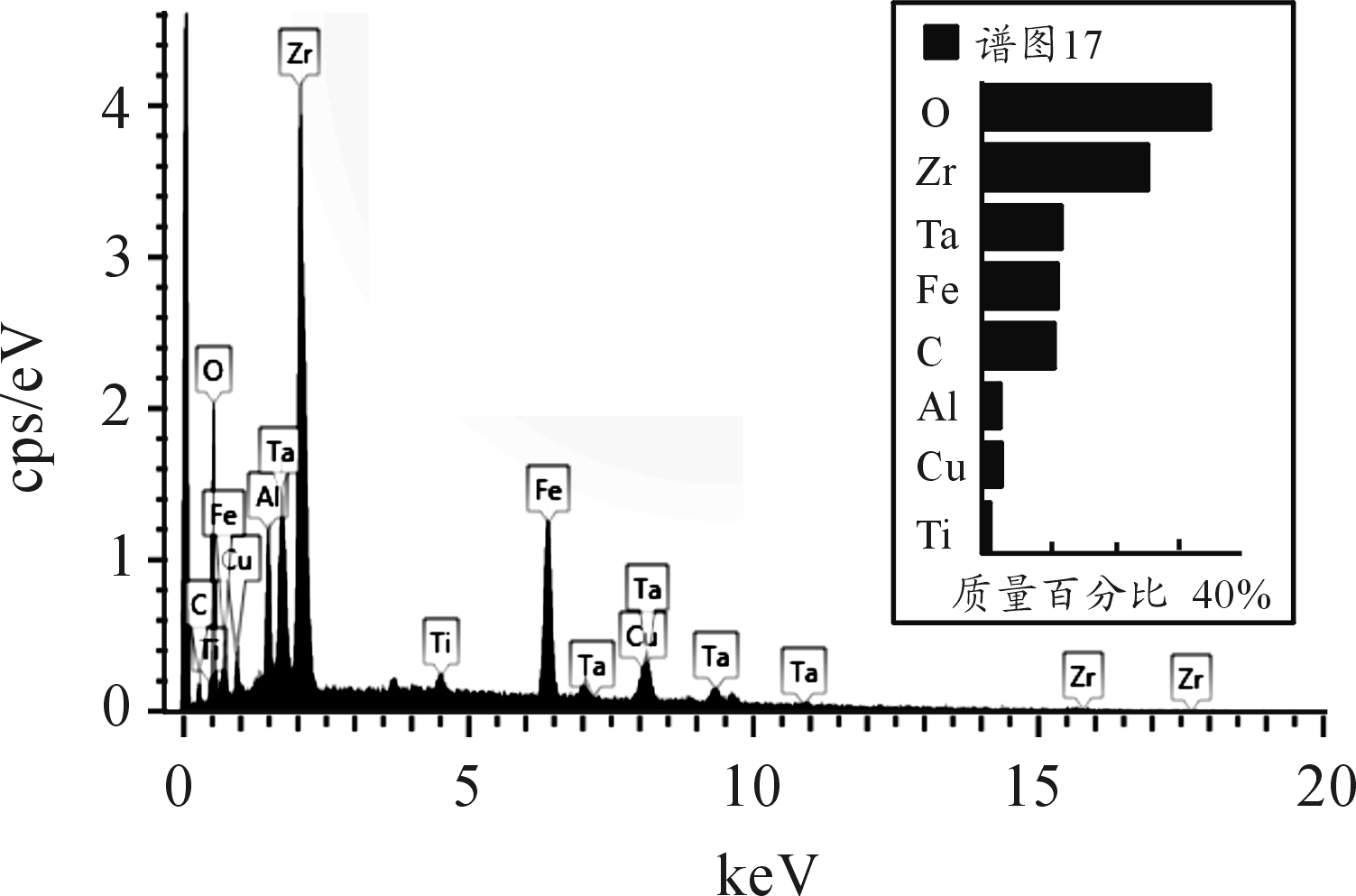
图10 1 mmZr/3 mmTa双层药型罩后效铝靶表面残留物EDS分析结果

图11 60 mm Cu基准罩后效铝靶表面残留物EDS分析结果
4 结论
1) 基于60基准罩而设计的锆/钽双层含能药型罩形成EFP的弹丸长径比较小,速度衰减快。
2) 内外罩厚度比一定时,6到9倍口径炸高处EFP的速度最大和侵彻能力最强;当炸高继续增大的情况下,EFP的速度和侵彻能力有所降低。
3) 相同装药和炸高条件下,锆/钽双层药型罩厚度比越大,形成的EFP速度越来越小,侵彻能力越来越弱,而扩孔能力差距不大。
4) 通过实验结果对比,1 mmZr/3 mmTa双层药型罩与60 mm基准罩侵彻深度和扩孔直径差距不大,但1 mmZr/3 mmTa双层药型罩具备很强的后效毁伤能力,在穿透目标靶板后,可利用其放热特性对靶后目标(例如,干草、棉絮、煤油等)有效引燃,可为高效聚能战斗部和含能药型罩的设计和研究提供参考。
[1] BUC S M.Shaped Charge Liner Materials:Resources,Processes,Properties,Costs,and Applications[R].System Planning Corp Arlington,1991.
[2] FAIBISH E,MAYSELESS M.A.Double-Layered Conical Liner Manufactured by Explosive.welding,5th International symposium on Ballistic[C].USA,International Ballistics Committee,1985.
[3] 臧涛成,贾建新,黄丽宏.用聚能装药多层药型罩提高射流速度的研究[J].弹道学报,1994,7(2):78-84.
[4] WEIMAN K,BLACHE A.Explosively formed projectile with tantalum penetration and steel stabilization base,18th International Symposium on Ballistics[C].San Antonio.USA,International Ballistics Committee,1999.
[5] 许世昌.双层含能药型罩射流成型机理及侵彻性能研究[D].南京:南京理工大学,2015.
[6] 刘亚昆.爆炸成型含能复合侵彻体的数值模拟研究[D].太原:中北大学,2018.
[7] 郑宇,王晓鸣,李文彬.模型参数对射流侵彻半无限靶板的影响研究[J].计算机仿真,2009,26 (1):39-41.
[8] 刘安帮.双金属复合药型罩特性分析[C]//破甲技术文集四.北京:国防工业出版社,1982,158-162.
[9] MELVIN A.Cook.The Science of Industrial Explosives[M].Ireco Chemicals,1974.
[10] 孙加肖,尹建平,王志军,等.双层椭圆形药型罩装药射流成形时长短轴比、铝铜铁三种材料的声阻抗和罩间距三因素正交设计研究[J].兵器装备工程学报,2016,37(6):135-139.
