Citation format:ZHAO Keyi, XIANG Hongjun, SUN Liping, et al.Structure Design of Two Kinds of Electromagnetic Catapult and Their Dynamic Catapult Performance[J].Journal of Ordnance Equipment Engineering,2019,40(7):70-75.
作者简介:赵科义(1973―),男,博士,副教授,主要从事电磁发射理论与技术研究,E-mail:keyizhao@sina.com。
doi: 10.11809/bqzbgcxb2019.07.015
电磁弹射器结构设计及其动态弹射性能
Structure Design of Two Kinds of Electromagnetic Catapult and Their Dynamic Catapult Performance
电磁弹射器通常用于舰载机和无人机等大质量载荷的弹射起飞 [1-2]。国内外在该领域做了大量的研究工作,取得了诸多重要研究成果[3-5],但在导弹电磁弹射方面的研究相对较少。美国桑迪亚国家实验室曾对导弹电磁发射器(Electromagnetic Missile Launcher,EMML)做了相关实验研究工作[6],采用了多级同步感应线圈炮的结构形式,多级驱动线圈同轴直线排列,工作时需依据电枢运动位置对驱动线圈适时馈电。这种弹射方式有利于将大质量载荷加速到高速,但其高效运行精确控制难。邹本贵等人曾对舰载导弹电磁线圈垂直发射方案进行了设计和仿真研究[7-8],采用了与桑迪亚国家实验室类似的结构方案。王秋良等人系统分析了同轴线圈电磁推进技术关键技术及技术瓶颈可能的解决途径[9]。
针对弹射速度要求不高的场合,如导弹冷发射,只需利用电磁弹射器将导弹载荷弹射到安全距离之外,再启动火箭发动机工作即可。但目前研究较多的脉冲感应型电磁弹射装置的弹射效率普遍较低[6,10],且弹射大质量载荷需要消耗大量的储能,因此设计高效电磁弹射器对大载荷助推弹射具有重要意义。本文基于脉冲感应电磁弹射原理,通过驱动线圈与电枢结构设计,提出了两种不同结构的电磁弹射器设计方案,建立了动力学模型,并在特定工况下对其动态弹射性能进行了计算仿真,研究,分析了电枢与驱动线圈之间的磁耦合情况,探讨了驱动线圈的加固问题。
1 电磁弹射器的结构设计与工作原理
1.1 电磁弹射器结构设计
电磁弹射器结构1如图1(a)所示,主要由一个圆筒状驱动线圈和一个圆形杯状电枢构成。这种结构与感应线圈炮结构类似,但其电枢结构不同于感应线圈炮中通常采用的圆筒状电枢。电磁弹射器结构2如图1(b)所示,主要由三个同轴嵌套的驱动线圈和与这三个驱动线圈布局结构相匹配的齿槽状电枢构成。这两种结构的电磁弹射器均关于Z轴轴对称。在电磁弹射器结构2中,三个驱动线圈沿径向(即X轴或Y轴方向)由外向内依次为驱动线圈1、驱动线圈2和驱动线圈3,电枢具有前端齿和后端齿,电枢尾部具有两个圆环形槽和三个圆环形齿,圆环形槽内可容纳驱动线圈2和驱动线圈3。被弹射的有效载荷可安装于电枢前端或前端齿之间。电磁弹射器结构2之所以采用三个驱动线圈和电枢齿槽啮合结构布局,其目的主要是为了改善驱动线圈与电枢之间的磁耦合性能,从而提高电磁弹射器的弹射效率或动态弹射性能。
将电磁弹射器结构1和电磁弹射器结构2分别简称为结构1和结构2。结构1中的驱动线圈和结构2中的驱动线圈1结构尺寸完全相同,相应的电枢外直径和轴向长度也完全相同。驱动线圈的径向厚度均为27 mm。驱动线圈1的轴向长度为150 mm,驱动线圈2和驱动线圈3的轴向长度均为100 mm。电枢与驱动线圈之间的间隙距离均为3 mm。驱动线圈1的内直径为306 mm。电枢前端齿和后端齿的径向厚度均为30 mm,前端齿和后端齿的轴向长度分别为50 mm和73 mm,前端齿和后端齿之间部分的电枢轴向长度为40 mm。电枢外直径和轴向长度分别为300 mm和163 mm。
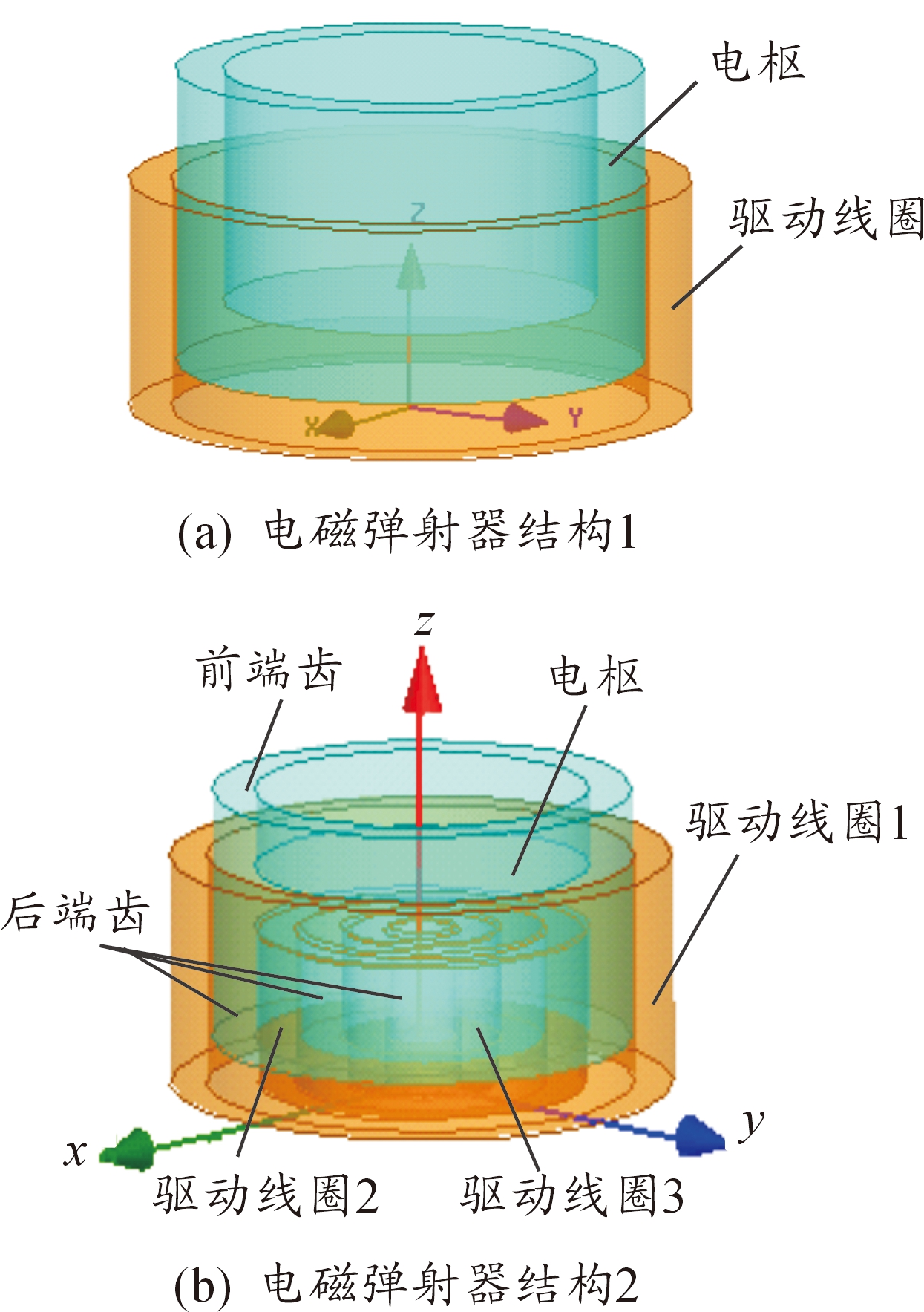
图1 电磁弹射器结构示意图
1.2 电磁弹射器的工作原理
这两种电磁弹射器工作时均需脉冲功率电源对驱动线圈放电,放电产生的脉冲电流流过驱动线圈时会在驱动线圈周围产生脉冲强磁场,使铝质电枢上感生涡流。如果电枢内感应电流密度为J,电枢所在处的磁感应强度为B,则电枢受到的电磁力F可表示为
![]()
(1)
式中,V为电枢的体积。由于结构1和结构2均关于Z轴轴对称,所以电枢受到的径向电磁力也是关于Z轴对称的、且相互抵消。这样,电枢仅受到沿Z轴方向上的电磁力作用,致使电枢及载荷沿Z轴方向加速运动而被弹射出去。由于电枢电流是通过电磁感应产生的,电枢与驱动线圈之间的磁耦合性能越好,则越有利于电枢电流产生,因此改善电枢与驱动线圈之间磁耦合情况有助于提高电磁弹射器的动态弹射性能。
1.3 动力学模型及求解方法
考虑到电枢内感应涡流分布是不均匀性,可将电枢视为多个丝状电枢圆环,并假定每个丝状电枢圆环内的电流是均匀分布的。这样,基于储能脉冲电容器放电驱动的结构1和结构2系统的等效电路模型分别如图2(a)和图2(b)所示。
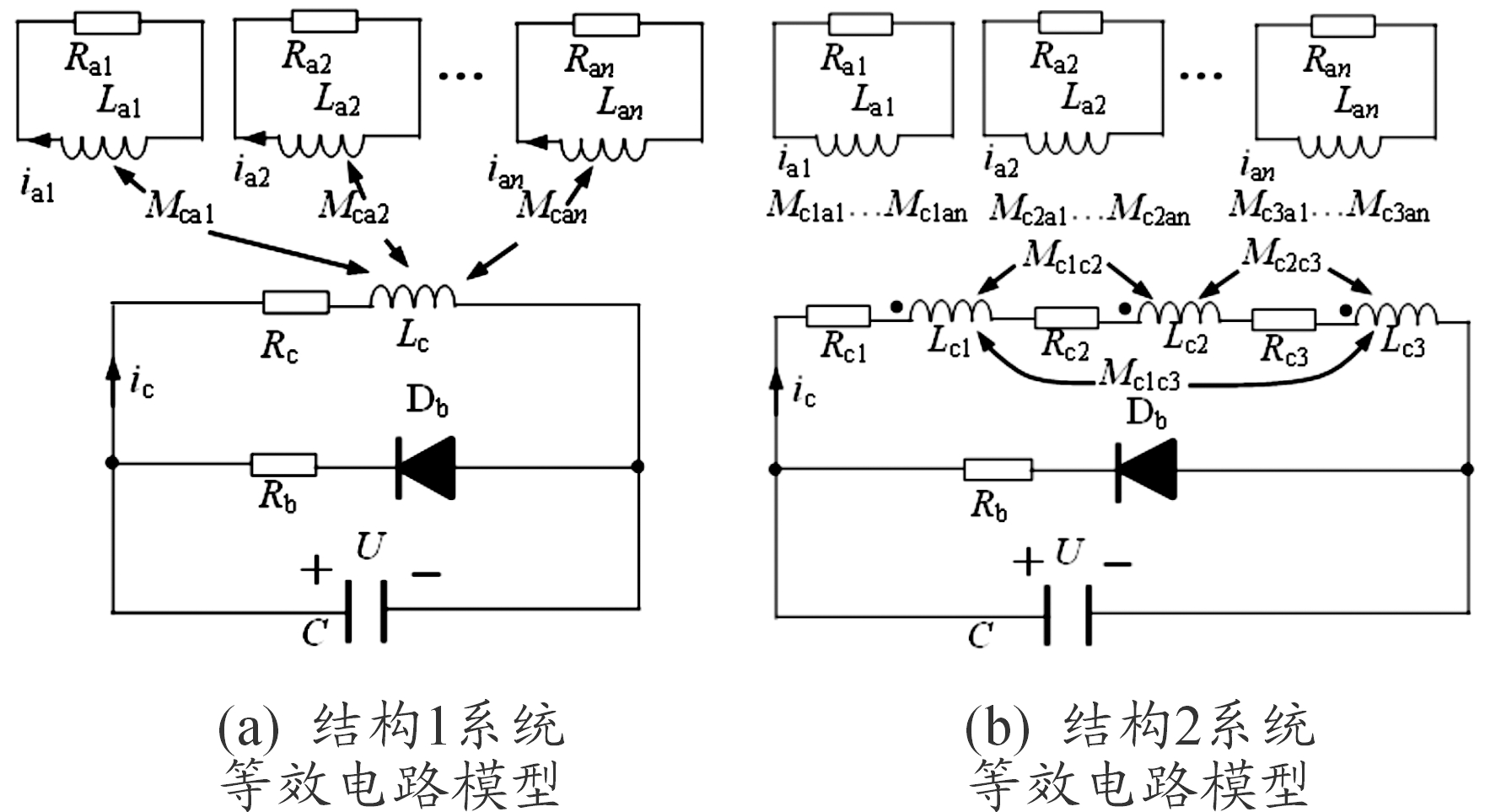
图2 电磁弹射器结构1和结构2系统等效电路模型
Rb和Db构成续流支路;Rc、Rc1、Rc2、Rc3、和Lc、Lc1、Lc2、Lc3分别表示各驱动线圈的电阻和自感;C和U分别表示储能脉冲电容器的容量和电压;Mca1…Mcan、Mc1a1…Mc1an、Mc2a1…Mc2an和Mc3a1…Mc3an表示相应驱动线圈和丝状电枢圆环间的互感。图2中各丝状电枢圆环间的互感中未标出。结构2系统对应的等效电路模型中的三个驱动线圈顺串连接,保证了其工作时磁极极性相同。依据图2所示的等效电路模型,可以建立矩阵形式的电路方程[11],即
![]()
(2)
式中,为自感矩阵、电阻矩阵、电流矩阵、电压矩阵、电流对时间的导数矩阵、互感梯度矩阵和互感矩阵,v为电枢运动速度。对于结构1而言,续流支路作用前,式(2)中的各矩阵分别为
续流支路作用后,电压矩阵变为零矩阵,电阻矩阵中的元素Rc变为Rc+Rb。
对于结构2而言,电感矩阵[L]中的元素Lc需修改为Lc1+ Lc2+Lc3+ 2Mc1c2+2Mc2c3+2Mc1c3;电阻矩阵[R]中的元素Rc需修改为Rc1+ Rc2+Rc3;电流矩阵、电流对时间的导数矩阵和电压矩阵保持不变。互感梯度矩阵和互感矩阵需修改为
弹射过程中储能脉冲电容器两端的电压可表示为
(3)
式中,U0为电容器的初始电压。由式(2)变形可得
![]()
(4)
弹射过程中,从弹射器内磁场储能随电枢位置变化的角度考虑,则电枢沿Z轴受到的电磁力为[11]
FZ=[I]T[M1][I]
(5)
结合初始条件 [I]t=0=0和式(4)可得离散化,离散时间步长为Δt,则第j个时间步长对应的电流矩阵与第j-1个时间步长对应的电流矩阵关系为这样,通过叠代方法可以求出任意时刻的[I],进而可由式(5)求得电枢受到的电磁力。
第j个时间步长内电枢及载荷运动的加速度为
aj=(Fzj-G)/m
(6)
式中,G和m分别为弹射的总重量和总质量。
第j个时间步长结束时电枢及载荷的速度和位移分别为
vj=vj-1+aj(Δt)
(7)
sj=sj-1+vj-1(Δt)+0.5aj(Δt)2
(8)
利用式(2)、式(3)、式(5)、式(6)、式(8),同时结合初始条件即可描述电磁弹射器的动态弹射过程。弹射过程中由于电枢位置的不断变化,致使电枢与驱动线圈之间的互感和系统等效输入阻抗也在不断变化,从而影响储能脉冲电容器的放电情况。驱动电流的变化又会影响驱动线圈周围的脉冲强磁场和电枢内感应涡流,从而对电枢受力产生影响。因此,动态弹射性能仿真时需要采用电路与磁场相互耦合的仿真方法,并在每一时间步长内首先依据电枢位置来计算电感等参数,再结合式(4)计算驱动电流,进而计算电枢的受力、加速度、速度和位移等参数。
2 电磁弹射器动态弹射性能仿真
2.1 对比研究的相关假定
由于结构1和结构2所采用的驱动线圈个数不同,对应的电枢形状也不同,所以两者对应的驱动回路参数也不同。为使结构1和结构2的动态弹射性能具有可比性,现假定如下:(1)被弹射的电枢与载荷的总质量相同,均为500 kg;(2)驱动用脉冲功率电源参数完全相同,即储能脉冲电容器的容量均为20 mF,初始放电电压均为10 kV;(3)弹射时电枢所处的初始位置相同,电枢末端均距离X轴30 mm;(4)均考虑电枢及载荷自重的影响,但均忽略空气阻力的影响。
在上述假定下,通过比较结构1和结构2在弹射过程中电枢及载荷所获的动能与消耗的脉冲功率电源储能之比的方法,即通过弹射效率分析的方法即可衡量这两种电磁弹射器动态弹射性能的优劣。
2.2 仿真模型的建立
Ansoft电磁场有限元分析软件中的瞬态求解器可用于运动导体的计算问题[12],故采用其进行建模。由于结构1和结构2均为轴对称结构,所以建立二维轴对称仿真模型,如图3。整个外边框包围的区域为求解区域,内边框所包围的区域为电枢运动区域。
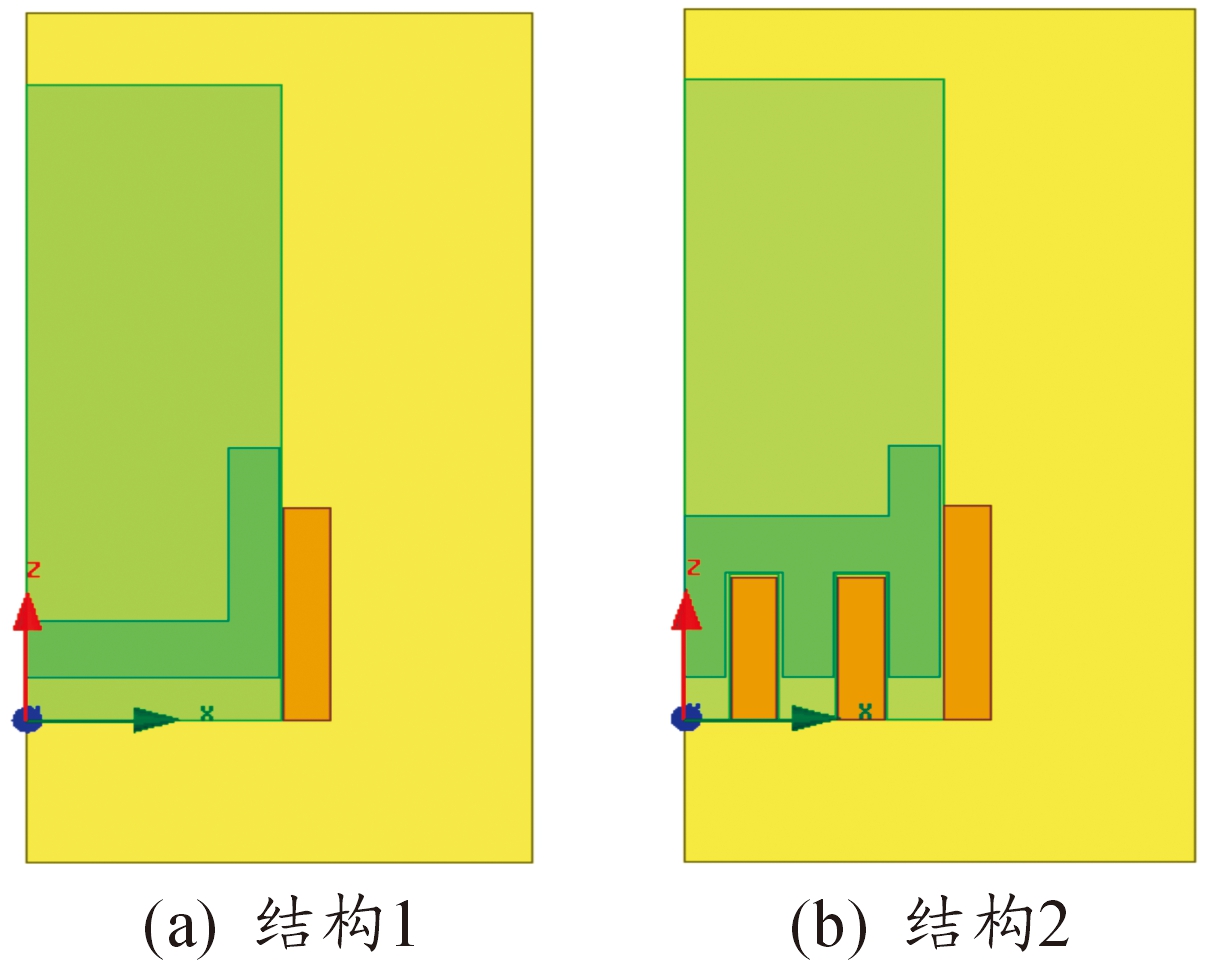
图3 两种不同结构的电磁弹射仿真模型
2.3 动态弹射性能仿真及结果分析
仿真过程中,均采用了外电路加载方式。结构1和结构2对应的驱动电路分别如图4(a)和图4(b)所示。图4(a)中驱动线圈的匝数为120匝,设其直流电阻Rc1为180 mΩ;图4(b)中驱动线圈1、驱动线圈2和驱动线圈3的匝数分别为120匝、80匝和80匝,设其直流电阻Rc1、Rc2和Rc3分别约为180 mΩ、76 mΩ和30 mΩ。这里给出的各驱动线圈的直流电阻是依据其结构参数和匝数计算得到的,仿真时需将其与驱动线圈串联。本文对结构2在磁极极性相同驱动方式下的动态弹射性能与结构1的动态弹射性能进行对比研究。
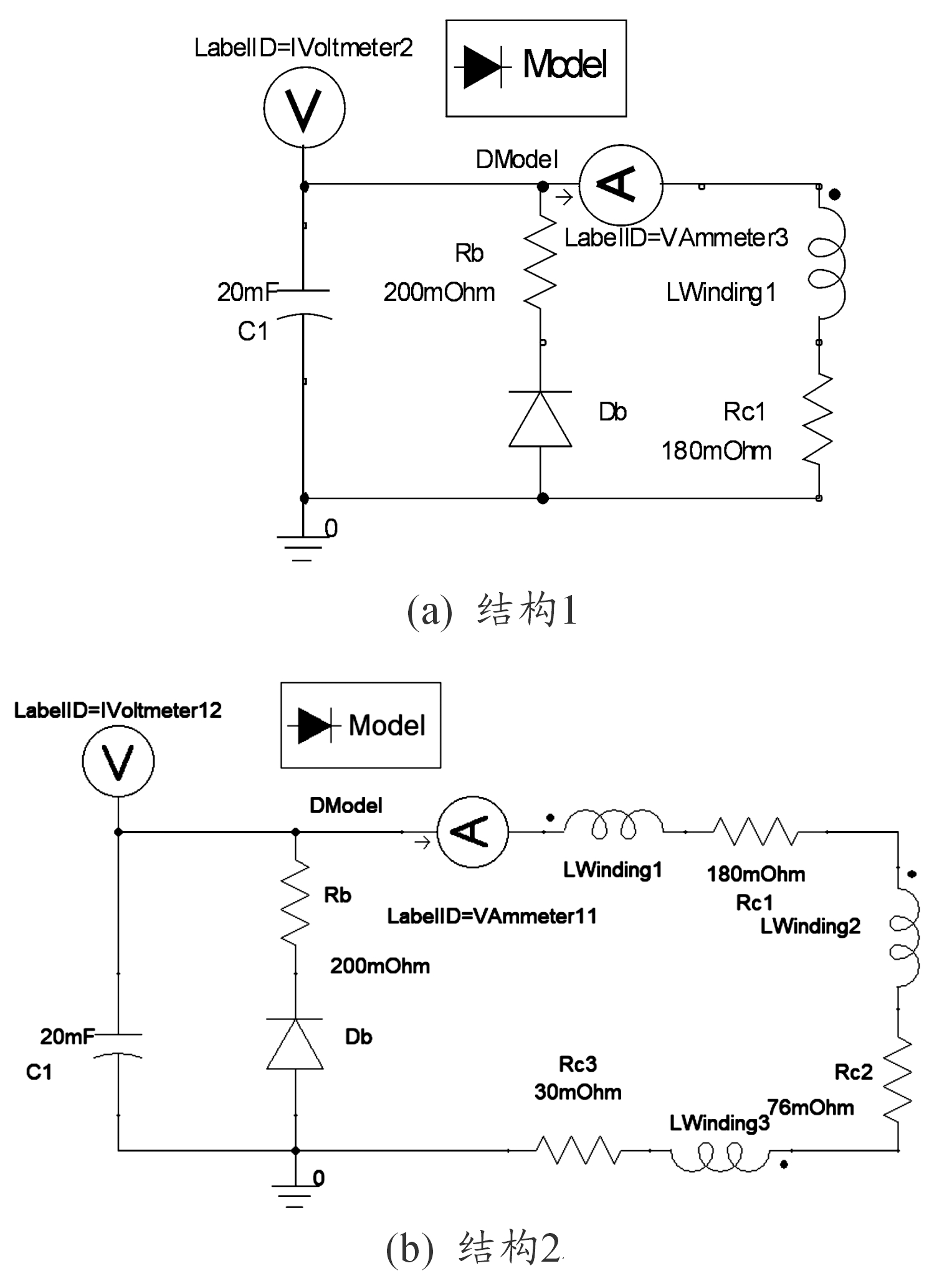
图4 结构1和结构2的驱动电路
将驱动线圈和电枢的材料分别设置为铜和铝。设电枢的初始速度为0 m/s,电枢及载荷的总质量为500 kg。在垂直弹射的情况下,设置负载力为电枢及载荷的总重量5 000 N。
图5中(a)、(b)、(c)、(d)、(e)分别给出了这两种不同结构电磁弹射器在上述工况下的动态弹射性能,即驱动电流I、储能脉冲电容器两端的放电电压U、电枢受到的电磁力F、电枢的运动速度v和运动位移p随时间变化的规律。
由图5(a)可知,结构1在弹射过程中驱动电流峰值相对较大,且约于5.8 ms达最大值17.187 kA;结构2在磁极极性相同的驱动方式下对应的驱动电流峰值相对小得多,且于4.68 ms达到最大值11.038 kA。由图5(b)可知,结构2在磁极极性相同的驱动方式下储能脉冲电容器放电比较缓慢,而结构1在弹射过程中储能脉冲电容器放电相对更快。
由图5(c)和图5(d)可以看出,结构2的动态弹射性能相对更好,电枢受到的电磁力相对更大(约于5.8 ms时达到最大值2.078 MN),所获得的运动速度也相对更大(约于12.14 ms时获得最大速度24.44 m/s)。结构1的动态弹射性能相对稍差,弹射过程中电枢约于6.46 ms获得约1.66 MN的最大电磁力作用,并约于13.22 ms获得23.56 m/s的最大速度。结构1和结构2中的电枢分别约于13.4 ms和12.1 ms开始受到制动性电磁力的作用,对应的运动位置分别约为158 mm和155 mm。电枢运动位移如图5(e)所示。由结构参数可知:电枢受制动力作用时,结构1中电枢末端已越过了驱动线圈前端面约38 mm;结构2中电枢尾部也已越过了驱动线圈1的前端面约35 mm。
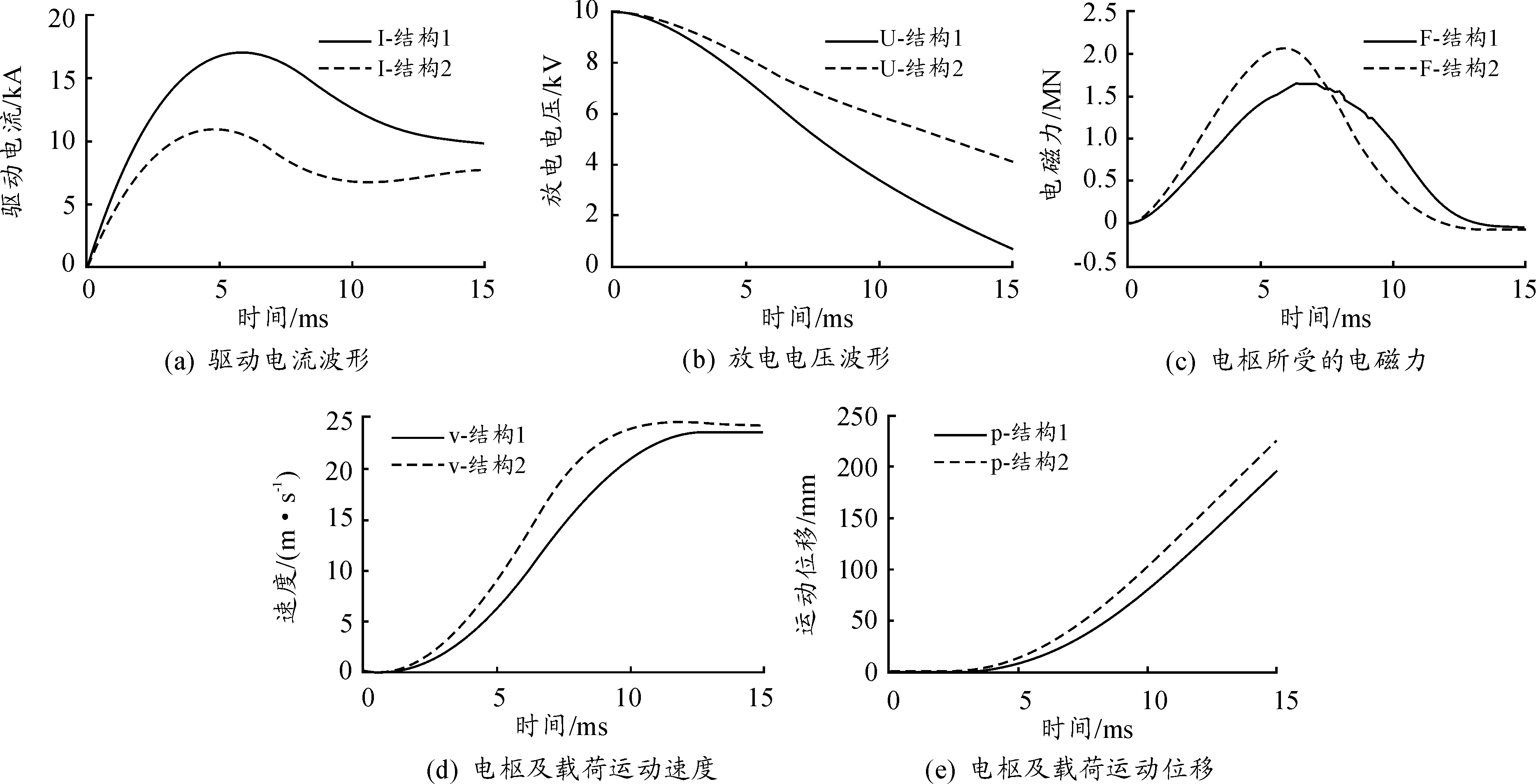
图5 两种不同结构电磁弹射器动态弹射性能曲线
2.4 效率分析
为评价这两种不同结构电磁弹射器的动态弹射性能,下面从弹射效率的角度进行衡量。从图5(c)和图5(d)可以看出,尽管电枢在弹射末期均会受到制动电磁力的作用,但制动电磁力相对较小,对运动速度影响不大。因此,可依据获得的最大动能与获得最大动能时储能脉冲电容器所释出来的能量之比来衡量其弹射效率。据此可将弹射效率表示为
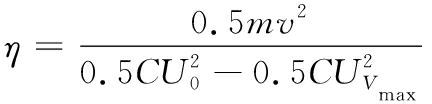
(9)
式中,U0=10 kV,UVmax为获得最大速度时储能脉冲电容器两端的电压。对结构1和结构2而言,获得最大速度时UVmax分别约为1.57 kV和5.17 kV。依据这些数据和式(9),对结构1和结构2计算所得的弹射效率分别约为14.23%和20.38%。这意味着在获得最大速度之后,如果能够对储能脉冲电容中的剩留储能进行回收,则结构2在可获得相对高得多的弹射效率。
由于结构2在获得最大速度时仍具有大量的系统储能,包括储能脉冲电容器中的电场能量和驱动回路电感中的磁场能量,所以对结构2系统中的剩留储能进行回收是有必要的。回收系统剩留储能的方法是:在电枢及载荷获得最大速度时,断开储能脉冲电容器使其停止放电,同时通过换路措施对驱动线圈中储存的磁场能量进行回收,即让驱动电流对另一组储能脉冲电容器充电。如果能够对系统中的剩留储能全部予以回收,则结构2的弹射效率将会高于20.38%。这为高效电磁弹射器的设计提供了一种实现方法和思路。
如果不能对电枢及载荷获得最大速度后的系统剩余能量进行回收,则需依据电枢及载荷获得的最大动能与储能脉冲电容器初始储能之比来衡量电磁弹射器的弹射效率,即依据式(10)评价弹射效率。

(10)
依据式(10)计算的结果为:结构1的弹射效率约为13.88%;结构2在磁极极性相同的驱动方式下对应的弹射效率约为14.93%。这表明:在不能对电磁弹射器系统中的剩余储能进行回收时,结构2在磁极极性相同驱动方式下的弹射效率仍稍好于结构1的弹射效率,但其弹射效率优势已并不明显。
结构2系统能在储能脉冲电容器放电相对较少的情况下获得最大运动速度,这使得通过回收系统剩留储能来提高弹射效率成为可能;而结构1中储能脉冲电容器只有释放出约90%的初始储能才能获得最大速度,故对结构1系统中剩留储能回收意义不大。
2.5 电枢与驱动线圈间的磁耦合情况分析
电枢与驱动线圈之间磁耦合情况会直接影响电枢内感应电流和电磁力分布,进而影响弹射性能。为比较结构1和结构2中电枢与驱动线圈之间的磁耦合情况,取电枢运动位移均约为20 mm时情况进行说明。结构1中的运动位移约为20 mm时对应于时间t=6.24 ms,相应的驱动电流约为17.08 kA,对应的电流分布情况图6(a)。结构2中的运动位移约为20 mm时对应于时间t=5.6 ms,相应的驱动电流约为10.73 kA,对应的电流分布情况如图6(b)。
从图6(a)可以看出:电枢内感应涡流的分布是很不均匀的,主要集中在电枢尾部外边缘处,并依次由径向向内和沿Z轴正向逐渐变小;而从图5(b)可知,电枢内的感应电流分布虽然仍集中在尾部齿区域,但是从整体上来看,电枢内感应电流的分布相对均匀得多。这说明结构2与结构1相比,能更好地实现电枢与驱动线圈之间的磁耦合。这也正是结构2在储能脉冲电容器放电相对较少条件下就能获得最大运动速度的原因,从而为回收系统剩留储能、提高弹射效率提供了可能。
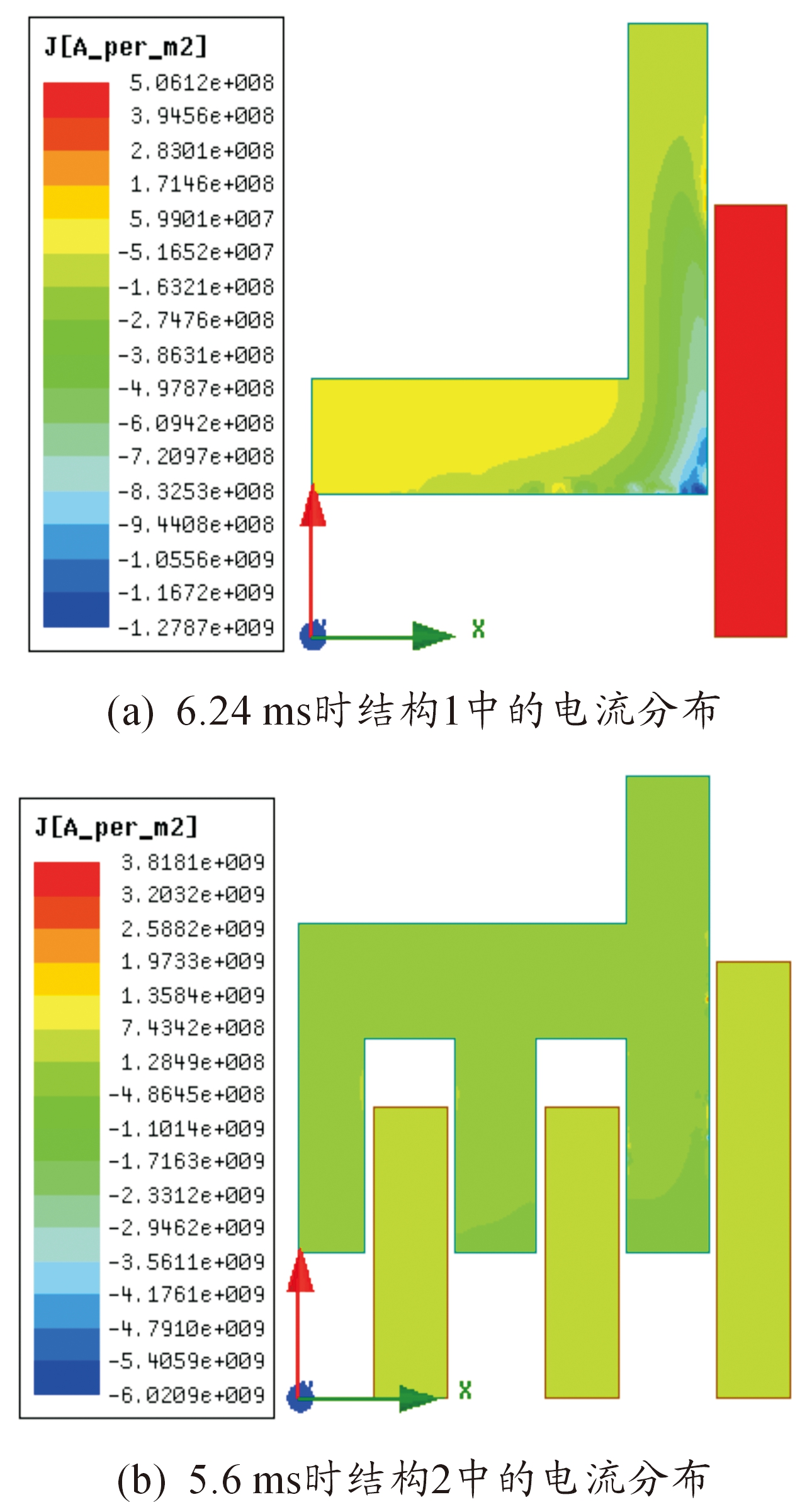
图6 驱动线圈和电枢内的电流分布
2.6 驱动线圈加固问题探讨
结构2中三个同轴安装的驱动线圈在弹射过程中会受到很大电磁力的作用,因此必须采用高强度、非磁性复合绝缘材料对其可靠加固。在实际设计过程中,可采用玻璃纤维、凯夫拉、柴龙等[9]高强度复合材料分层、分角度缠绕,并对缠绕后的驱动线圈利用环氧树脂真空灌注一体化封装等措施。当然,还需要反复计算驱动线圈受力及加固结构在受电磁力作用下的应力应变情况。当不能获得高强度加固材料或加固强度不够时,应通过适当增大电枢与驱动线圈间的间隙距离,增加加固结构厚度来实现驱动线圈的可靠加固,当然这会牺牲弹射效率。
3 结论
与结构1相比,结构 2能更好地实现电枢与驱动线圈之间的磁耦合,使电枢内感应电流分布相对更均匀、电枢受到电磁力不仅更大而且相对更均匀、动态弹射性能相对更好。在电枢及载荷获得最大运动速度之后,如果不能对整个电磁弹射器系统中的剩留储能进行回收,则结构2的动态弹射性能稍好于结构1的动态弹射性能,如果能够对储能脉冲电容器中剩留的储能进行回收,则结构2显著提高弹射效率至20.38%。结构2与剩留储能回收相结合的方法将成为提高弹射效率的重要实现途径。
[1] 张明元,马伟明,汪光森,等.飞机电磁弹射系统发展综述[J].舰船科学技术,2013,35(10):1-5.
[2] 张安平.无人机电磁弹射技术研究[J].沈阳航空工业学院学报,2007,24(4):17-19.
[3] 吴峻,宋蕾,周文武,等.定子磁钢轨道拼接错位对动圈式永磁直线电机性能的影响[J].国防科技大学学报,2018,40(1):138-144.
[4] 许金,聂世雄,马伟明,等.无槽双边长定子直线感应电动机磁路计算方法[J].中国电机工程学报,2016,36(10):2793-2799.
[5] 高凯,吕小红.解析美国航母电磁弹射器[J].舰船知识,2012,(11):68-73.
[6] AUBUCHON M S,LOCKNER T R,TURMAN B N,et al.Results from Sandia National Laboratories/Lockheed Martin electromagnetic missile launcher (EMML) [J].IEEE Transactions on Magnetics,2005,41(1):75-78.
[7] 邹本贵,孙学锋,曹延杰,等.舰载导弹电磁线圈垂直发射方案设计[J].弹箭与制导学报,2013,33(5):45-48.
[8] 王旻,曹延杰,邹本贵,等.大载荷电磁线圈发射器相似条件研究[J].高压电器,2014,50(8):68-73.
[9] 王秋良,王厚生,李献,等.同轴线圈电磁推进技术评述[J].高电压技术,2015,41(8):2489-2499.
[10]SKURDAL B D,GAIGLER R L.Multimission electromagnetic launcher [J].IEEE Transactions on Magnetics,2009,45(1):458-461.
[11]王莹,肖峰.电炮原理[M].北京:国防工业出版社,1995,93-95.
[12]赵博,张洪亮.Ansoft12在工程电磁场中的应用[M].北京:中国水利水电出版社,2010: 130-180.
